信息技術助力開展高中數學探究活動的教學實踐探究

劉瑞紅

【摘要】在信息技術與教育快速融合的時代背景下，有效開展高中數學探究活動迎來了新的發展契機。本文以“函數y=Asin（ωx+φ）的圖象”為例，從信息技術助力開展數學探究活動的自主學習、合作學習和延伸學習三個方面，闡述了運用信息技術開展高中數學探究活動，促進發展學生數學核心素養的實踐研究。

【關鍵詞】信息技術;數學探究活動;數學核心素養

隨著科學技術的飛速發展，信息技術助力教育創新迎來新的春天。作為教育工作者，我們需要積極探索信息技術賦能數學教育教學的創新做法，致力于努力發展學生的數學核心素養。下面在信息技術助力開展數學探究活動方面進行了實踐探索，通過課前自主學習、課上合作學習和課后延伸學習，引導學生借助信息技術主動參與探究學習，實現線上線下、課內課外學習的融合，促進數學核心素養的發展。

一、信息技術助力開展數學探究活動的自主學習

1.創設情境? 自主建模

“函數y=Asin（ωx+φ）的圖象”是三角函數的一個重要內容，通過研究筒車的運動規律，學生經歷y=Asin（ωx+φ）的建模過程。如果課堂上，僅僅依靠文字描述和教師講解，不僅錯失了學生進行數學探究活動的大好機會，數學抽象和數學建模的能力得不到充分發展，而且弱化了中華古代文明的育人作用。

本節課，教師可以設計問題串創設情境，引導學生類比前面建立函數模型的經驗，上網搜索筒車運動和原理講解的視頻，開展自主探究性學習活動。通過觀察歸納和總結發現其中的規律，體會三角函數是描述周期現象的重要數學模型，提升學生的數學建模能力，發展學生的數學抽象、直觀想象、邏輯推理等核心素養。

問題1：筒車是我國古代發明的一種灌溉工具，因其經濟又環保，至今還在農業生產中使用。明朝科學家徐光啟在《農政全書》中用圖畫描繪了桶車的工作原理。請你搜索筒車運動和講解運動原理的視頻資料，研究盛水桶在運動中有何規律？可以抽象出哪些數學對象？你能想到用什么知識來刻畫他們之間的關系？

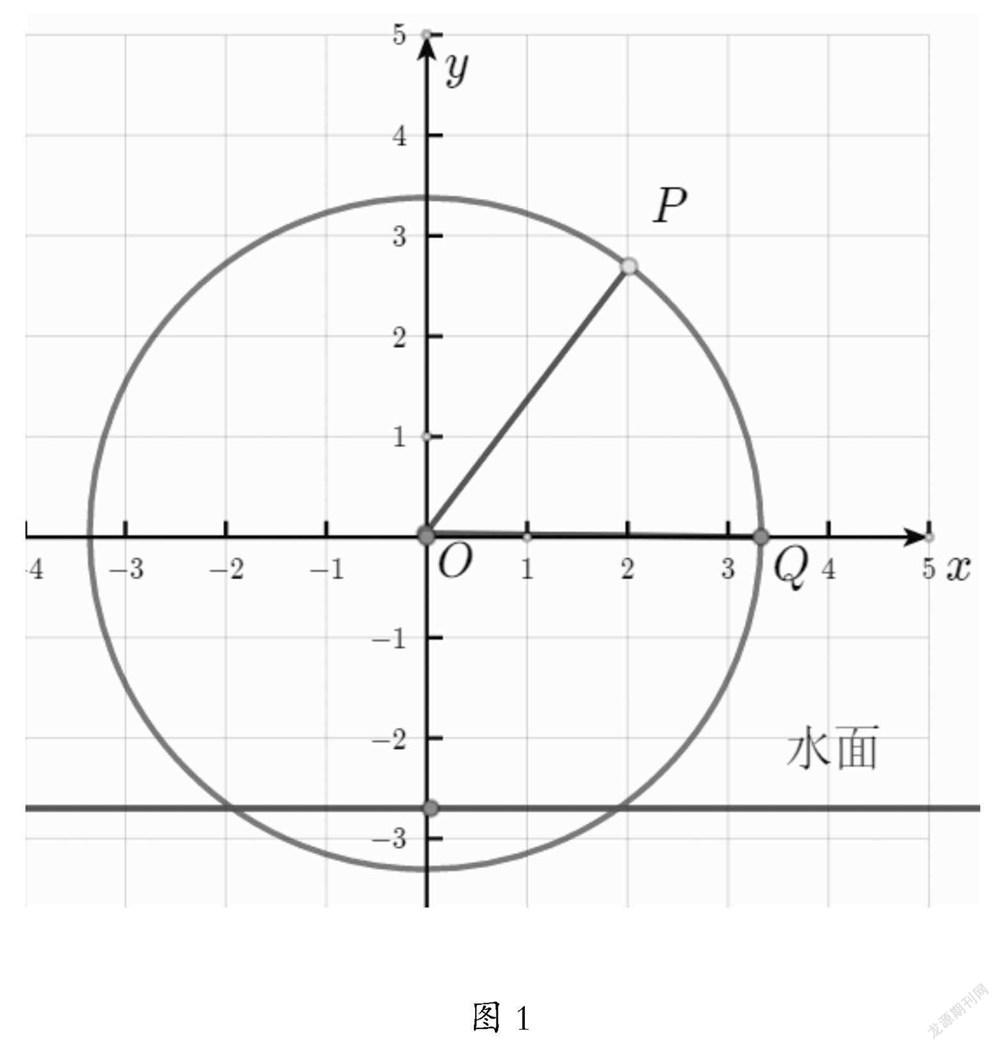
問題2：借助信息技術用幾何形式動態呈現點P的運動狀態（見圖1）。如果已知筒車半徑為r，盛水桶的初始位置Q1，對應的初始角φ及轉動的角速度ω，還有筒車轉輪的中心O到水面的距離h，你能刻畫點P的坐標嗎？

問題3：你能用函數模型刻畫水桶距離水面的相對高度H與時間t的關系嗎？請和同學們分享你的探究成果。

通過創設情境，拓寬學習資源，讓學生經歷建立筒車模型y=Asin（ωx+φ）的過程，引導學生用數學的眼光觀察世界，從生活中抽象出數學模型，學會用數學的語言描述世界。同時分享探究成果給學生以成就感，老師還可以根據學生完成的情況，開展個性化、有針對性的指導，在課堂上對三角函數模型的建立進行適當的關鍵補充，提升教學效率。

2.搭設臺階? 自主探究

在理解參數φ、ω、A在圓周運動中的實際意義后，可以在電腦室或者借助學習平板等教學設備，引導學生探究φ、ω、A對y=sin（x+φ）、y=sin（ωx+φ）（ω>0）、y=Asin（ωx+φ）（A>0）的圖象影響，在探索、觀察、歸納的過程中，發展數學核心素養。課上，教師提供兩個學習資料，一個是網絡畫板呈現的可以控制系數變化的函數y=Asin（ωx+φ）（A>0，ω>0）的圖象，一個是五點法作函數圖象關鍵點的Excel列表。借助網絡畫板直觀演示對比，直觀感知，結合關鍵點列表，證實結論。

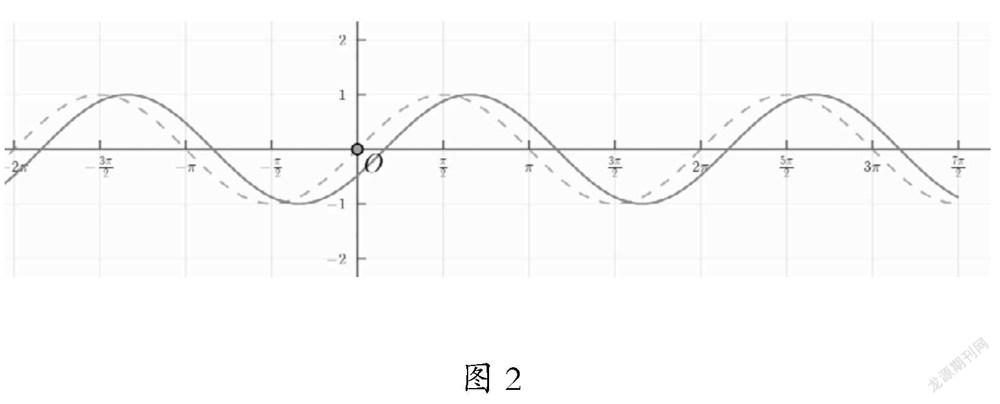
課堂預設：前面，我們已經借助單位圓得到過正弦曲線，用同樣的方法，我們也可以借助網絡畫板作出y=sin（x+φ）的圖象。（見圖2）

問題4：觀察φ分別取? ? ? ?，? ? ，? ?時，圖象發生怎樣的變化？動態演示圖象變化，你能否發現φ對函數y=sin（x+φ）圖象有怎樣的影響？

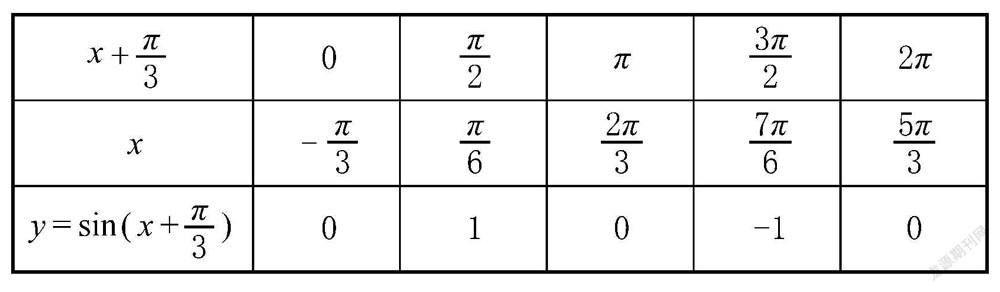
問題5：請觀察下面Excel表，由“五點法”可知，函數y= sin（x+? ? ?），x∈[0，2π]的五個關鍵點與函數y=sinx，x∈[0，2π]圖象上的五個關鍵點有什么關系？請總結改變參數φ，函數y=sin（x+φ）圖象可由y=sinx的圖象如何變換得到？

問題6：將函數y=3cos（x+? ? ? ） 的圖象向左平移

個單位所得函數圖象的表達式是什么？

借助信息技術，將抽象的、動態的變化過程直觀呈現給學生，加深學生對y=Asin（ωx+φ）的圖象變換規律的認識，滲透數形結合思想、從特殊到一般，從具體到抽象的思維方法，發展直觀想象和邏輯推理等數學核心素養。

二、信息技術助力開展數學探究活動的合作學習

在教學過程中，以學生為主體，充分借助信息技術組織數學探究活動，同時，信息技術平臺促進合作學習。ω對函數y=sin（ωx+φ）（ω>0）圖象的影響，既是本節課的學習重點，也是難點，由學生類比研究參數φ的方法合作探究完成。學生通過給同學分享講授，加深他們對知識的理解和自我建構，既促進了學生在數學探究過程中自主意識的發展，又培養了他們的合作精神。

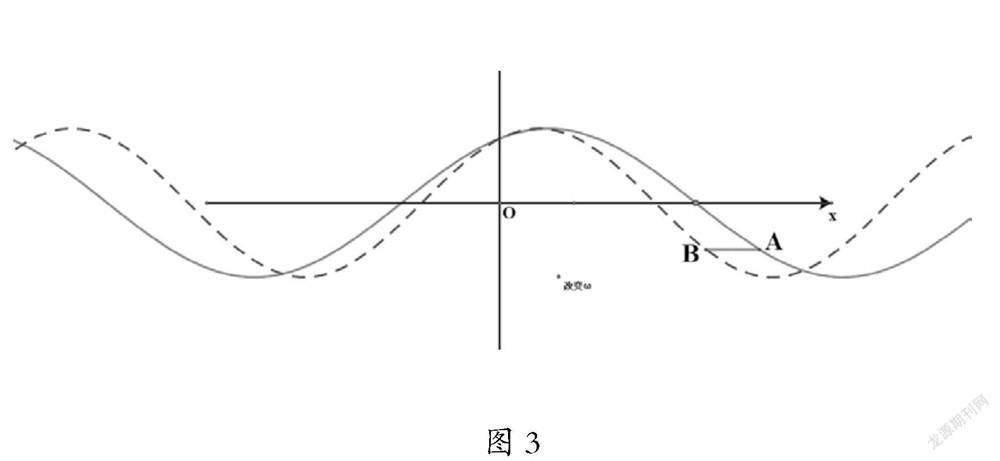
課堂預設：改變參數ω（ω>0）的值，用網絡畫板畫出函數y=sin（2x+? ? ?）的圖象，觀察分析函數數y=sin（2x+? ? ? ）與y=sin（x+? ? ? ）圖象的關系。（見圖3）

問題7：觀察分析參數ω（ω>0）變化后，圖象與y=sin（x+? ? ? ）的圖象有何變換關系？你能結合ω的含義是點在圓周上運動的角速度，來分析理解發生的變化嗎？

問題8：為得到y=sin（? ? ?x -? ? ?），x∈R的圖象，只需將函數 y=sin（x -? ? ?），x∈R的圖象上所有點的坐標如何變換？根據以上的實驗，在ω>0且ω≠1的情況下，參數ω（ω>0）變化后，對圖象的影響可分為幾類？你能總結出y=sin（ωx+φ）（ω>0）可以由y=sin（ωx+φ） 的圖象如何變換得到嗎？

教師引導學生開展小組合作，確定研究思路，合作探究，討論交流，借助信息技術，直觀感知圖象的伸縮變換，再數形結合分析坐標內在聯系，加深學生理解，突破本節課的重難點，發展學生核心素養。

數學知識的抽象性往往給學習帶來障礙，借助信息技術可以形象直觀、動態地展現函數圖象的變化聯系，幫助學生提升數學抽象思維能力以及邏輯推理能力，促進學生更好地理解和掌握數學知識。

三、信息技術助力開展數學探究活動的延伸學習

信息技術助力數學教學，實現了師生之間在課前、課中和課后的持續性學習溝通，增加了課堂的深度和廣度，使學習可以不斷延伸。教師積極搭建平臺，提供學習資源和技術支持，更好地使信息技術助力學生成長，尤其是運用信息技術的能力使學生能更好地不斷自我發展。

延伸學習作業：調整變換順序，由y=cosx的圖象變換得到y=? ? ?cos（2x-? ? ? ） 的圖象的變換方法是否變化？寫出三種不同順序的變換過程和方法，再用網絡畫板按照變換方法作出圖象進行檢驗，說說你的發現。

通過課后延伸學習，學生借助網絡畫板開展數學探究活動，為下一節課繼續學習y=Asin（ωx+φ）的圖象變換打下基礎，用網絡畫板作圖驗證，發現當ω≠1，即x的系數不為1時，平移量是? ? ?   ?，為突破易錯點進行鋪墊。

信息技術助力開展高中數學探究活動，以發展學生數學核心素養為目標，尊重學生為主體，使教學形式更多元，學習資源更豐富，學習過程更有趣。信息技術在幫助學生開展數學探究活動中的自主學習、合作學習和延伸學習方面有積極的促進作用，將抽象的數學知識以生動形象的方式呈現給學生，也將使用信息技術開展學習變成學生的一種能力，激發學生的學習興趣，提升學生的成就感。只有讓學生能夠學有所獲，才會喜歡學習數學，才能不斷地發展自身的數學思維能力以及數學核心素養。

參考文獻：

[1]劉邦奇，孫曙輝.智慧課堂[M].北京：北京師范大學出版社，2016.

[2]趙國宏.應用信息技術助力高中數學課堂教學之我見[J].數學學習與研究，2020.

[3]李久省，張程艷.發揮信息技術優勢 助力高中數學學習[J].北京教育（普教版），2020.