基于分數階Gabor變換的LFM回波信號壓縮采樣方法

王 強, 孟 晨, 王 成, 張 瑞

(陸軍工程大學石家莊校區, 河北 石家莊 050003)

0 引 言

線性調頻(linear frequency modulated, LFM)信號具有大的時寬帶寬積,能夠有效解決作用距離與距離分辨率之間的矛盾,在雷達、聲吶等探測系統中得到廣泛應用。在應用過程中,探測場景內不同的探測目標,使得偵察設備接收到的LFM回波信號表現為多個具有不同幅值與時延的回波分量的疊加。為準確提取LFM回波信號中的參數信息,需要對回波信號進行采樣,再利用處理器等相關設備進行信號的分析與處理。在Nyquist采樣定理下,信號采樣頻率至少是其最高頻率的兩倍。由于LFM信號頻帶較寬,為保證采樣過程不造成信息丟失,傳統A/D轉換器工作頻率較高,功耗較大。

基于壓縮感知理論的模擬信號壓縮采樣方法打破了Nyquist采樣定理對信號采樣過程的限制。該方法能夠以較低的采樣頻率與功耗完成對寬帶信號的采樣,并通過重構算法完成對原始信號的有效重構。現階段,壓縮采樣系統的具體實現形式仍在不斷發展中。目前,比較成熟的系統主要包括隨機解調器(random demodulator, RD)以及調制寬帶轉換器(modulated wideband converter, MWC)。二者對信號的重構過程,依賴于信號在頻域內的良好稀疏性,而LFM信號頻域稀疏性較差,因此傳統的RD以及MWC系統并不適用于LFM信號。針對這一問題,文獻[16]將RD系統重構階段中的傅里葉字典替換為分數階傅里葉字典,以實現對LFM信號的壓縮采樣與重構;文獻[17]提出了RD系統的廣義形式,并利用LFM信號在分數階傅里葉變換下的稀疏性,完成信號的重構;文獻[18]則提出了MWC的廣義形式,完成對分數階頻域多帶信號的壓縮采樣,該系統本質上也利用了信號在分數階傅里葉變換下的稀疏性,因此一定程度上適用于LFM信號。

從上述分析可以看出,現有的LFM信號壓縮采樣系統主要利用了信號在分數階頻域的稀疏性完成信號的壓縮采樣與重構。對于LFM回波信號,其在分數階頻域內的稀疏性還取決于探測場景內目標的個數。目標個數較多會導致稀疏度急劇增加,從而嚴重影響信號的重構效果。為此,本文提出一種具有時間-分數階頻域分析能力的分數階Gabor變換(fractional Gabor transform, FRGT)方法。該方法能夠利用不同目標回波信號在時延上的差異性,改善信號稀疏表示效果,從而改善LFM回波信號的壓縮采樣與重構效果。

1 問題描述

1.1 LFM回波信號模型

假設探測器發射的LFM信號為(),經過多個目標反射后,具有不同幅值、時延的回波信號會返回到信號接收機中。回波信號()可以表示為

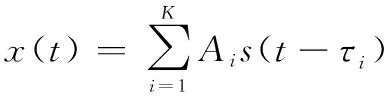
(1)

其中,

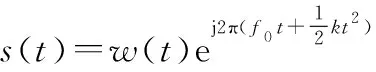
(2)

則

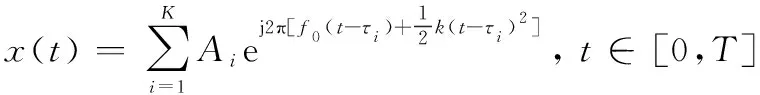
(3)

式中:為載頻;()為發射信號脈沖包絡;為LFM信號調頻率;、為第個回波分量的幅值與時延;為目標個數;為回波信號的總觀測時間。

1.2 分數階頻域稀疏性

對于信號(),其分數階傅里葉變換可以表示為

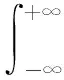
(4)

式中:(,)為核函數,定義為

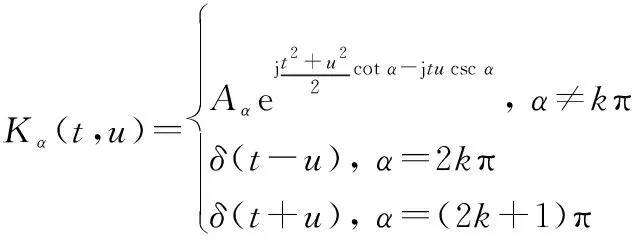
(5)

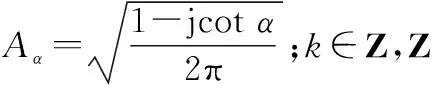
理想狀態下,當旋轉角度滿足=-arccot(2π·)時,信號()中單個分量在分數階傅里葉變換下的頻譜稀疏度為1。在實際應用過程中,發射信號()中的脈沖包絡()會導致分數階頻譜產生明顯泄露。中心頻率為0時的分數階頻譜如圖1所示,可以看出,泄露效應使得信號在分數階傅里葉變換下的稀疏度急劇降低,而目標個數的增加則使得稀疏度成倍增加。此時,基于分數階傅里葉變換的壓縮采樣與重構方法將不能取得良好的效果。

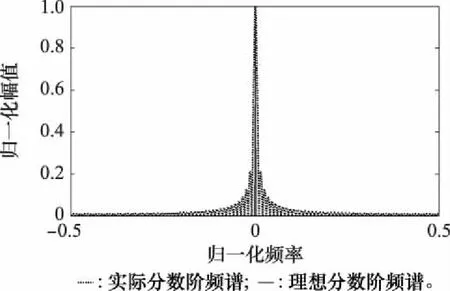
圖1 分數階頻譜的泄露效應Fig.1 Leakage effect of fractional spectrum

2 FRGT

2.1 FRGT定義

針對分數階傅里葉變換在LFM回波信號稀疏表示中的不足,本文提出了基于FRGT的信號分析方法。目前,FRGT是在傳統Gabor變換的基礎上,引入了分數階傅里葉變換因子,以使FRGT具有時間-分數階頻域的分析能力。考慮到壓縮采樣系統的實現問題,本文在現有的FRGT基礎上,提出了一種新的FRGT實現方法,該方法能夠保留現有FRGT在時間-分數階頻域的信號分析能力,同時更有利于壓縮采樣系統的設計實現。

本文FRGT定義為

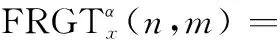
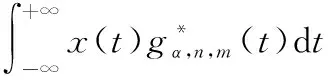
(6)

式中:(·)為共軛算子;,,()可以表示為

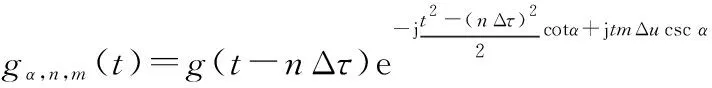
(7)

式中:()為窗函數。

在現有FRGT中,復指數平方項是時間以及分數階頻移Δ的函數,而在本文FRGT中,復指數平方項中的分數階頻移參數Δ替換為時移參數Δ。該過程并沒有改變FRGT在時間-分數階頻域的信號分析能力,但使得FRGT系數能夠通過濾波器獲得,因此更有利于壓縮采樣系統的設計實現。

2.2 完備性分析

FRGT需要具有完備性,保證信號經過變換后能夠得到完全重構。假設經過變換后,信號的重構過程為

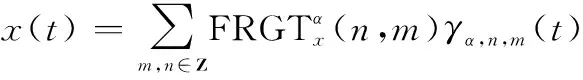
(8)

將式(6)代入,可得如下完備性條件:

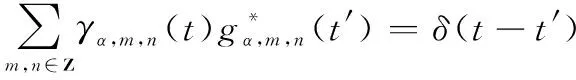
(9)

式中:()為delta函數。

進一步推導可得

(-′)=

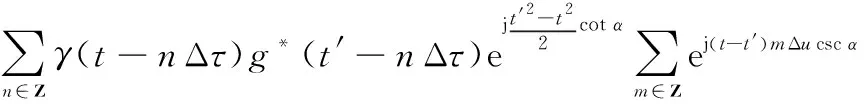
(10)

假設

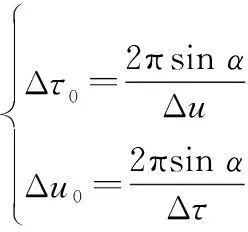
(11)

則根據泊松求和公式可得

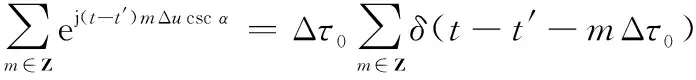
(12)

將式(12)代入:

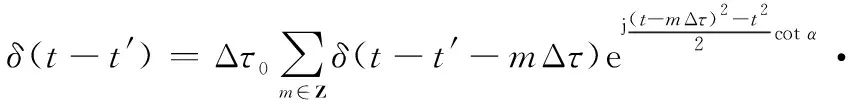
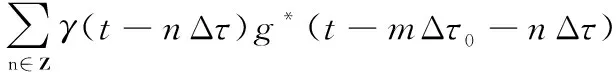
(13)

再次利用泊松求和公式可得

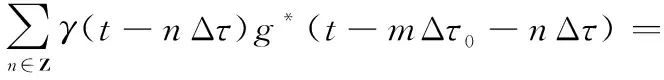
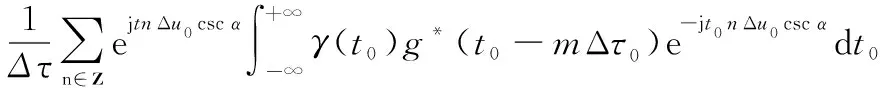
(14)

將式(14)代入,則有

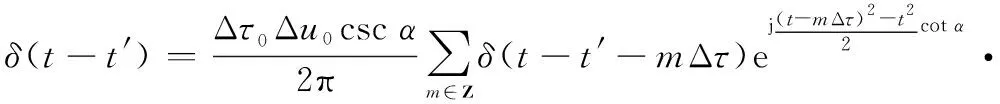
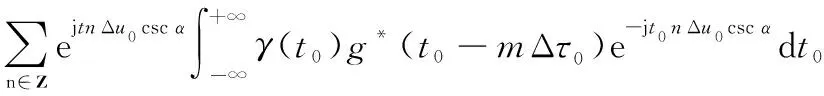
(15)

可以看出,等式成立的條件為

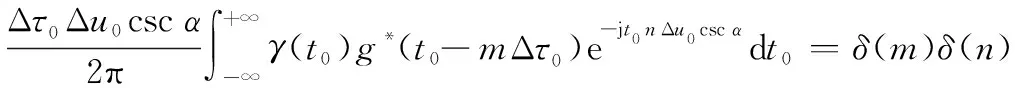
(16)

給定窗函數(),()可通過式(16)求得,此時信號可通過式(8)得到完全重構。

3 壓縮采樣與重構

3.1 濾波器設計

基于本文所提方法,FRGT系數可以表示為

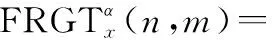
(17)

式中:*為分數階卷積算子,定義為

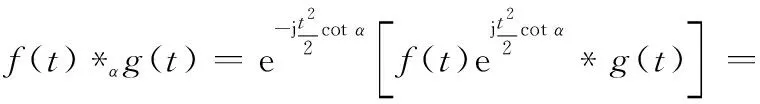
(18)

在分數階頻域,卷積算子具有如下性質:

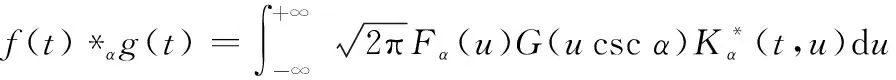
(19)

式中:()為()的分數階傅里葉變換;(csc)為()的傅里葉變換,則式(17)可以表示為

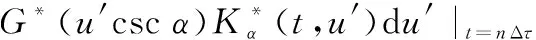
(20)

從式(20)可以看出,FRGT系數可以通過低通濾波的方式獲得。濾波器結構如圖2所示。

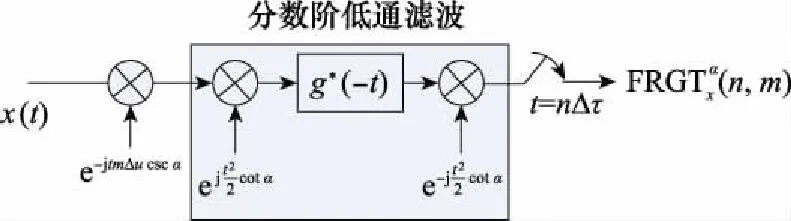
圖2 FRGT濾波器Fig.2 Filter for FRGT

3.2 信號的有限系數展開

根據不確定性原理,在[0,]內有限時域支撐的信號,在分數階頻域內是無限支撐的。但通常信號的能量會集中在有限的分數階頻帶范圍內,因此假設信號的分數階本質帶寬為[-2,2],滿足

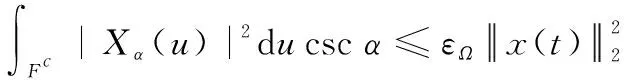
(21)

式中:為本質帶寬的補集;<1為常數。

同樣地,假設窗函數()的時頻域支撐集分別為[0,]以及[-2,2]。則信號能夠利用有限的系數進行近似展開:

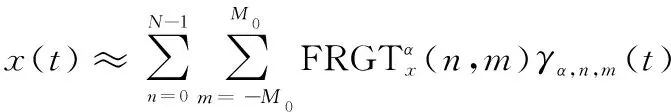
(22)

參數、可以通過下式確定:

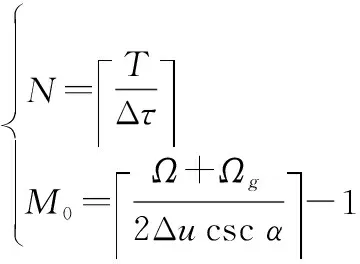
(23)

3.3 壓縮采樣系統設計與分析

在探測系統中,具有不同反射系數的目標會導致LFM回波分量具有不同幅值,而多個目標距離上的差異,則使得不同的回波分量具有不同的時延參數。FRGT具有良好的時間-分數階頻域分析能力,因此能夠有效利用各回波分量時延上的不同,改善信號的稀疏表示效果。

基于信號在FRGT下的稀疏性以及FRGT低通濾波的實現方式,本文提出了如圖3所示的LFM回波信號壓縮采樣方法。

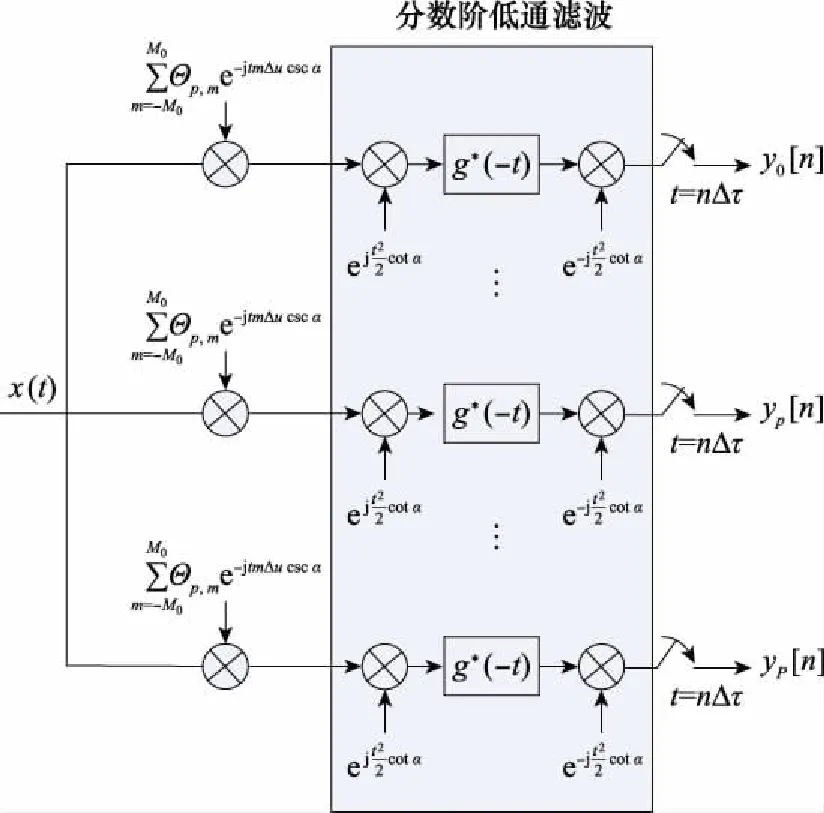
圖3 壓縮采樣系統Fig.3 Compressed sampling system

輸入信號()同時進入個采樣通道。在單個通道內,信號()首先與調制信號相乘;再經過分數階傅里葉域低通濾波器濾波;最后,采集器對濾波器輸出進行離散、量化,以完成單個通道內的壓縮采樣。采集器工作頻率為1Δ,整個系統的總采樣頻率為Δ。通過合理設置Δ以及,該采樣系統總采樣頻率能夠明顯低于Nyquist采樣頻率。在第個通道內,調制函數為不同頻率成分的加權,其中權值系數滿足高斯隨機分布。

在重構階段,首先利用壓縮采樣點完成對FRGT變換系數的重構,然后利用式(22)完成對原始信號的重構。在第個通道內,Δ時刻的采樣點可以表示為

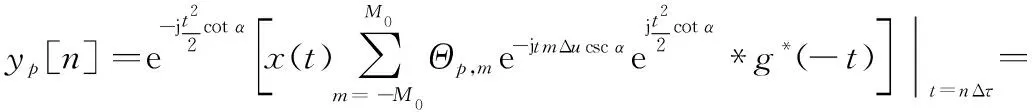
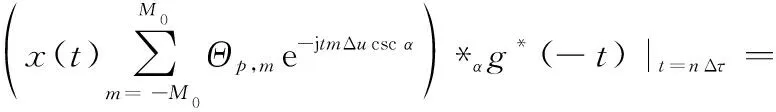
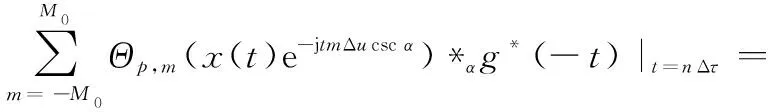
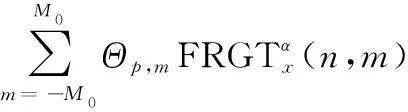
(24)

定義:

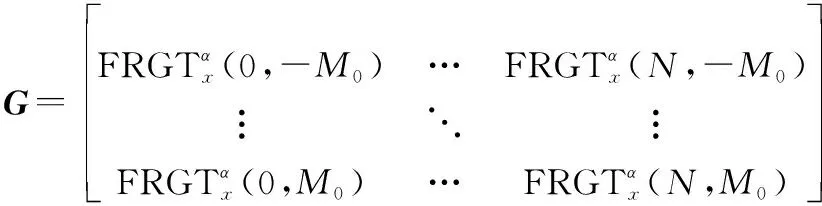
(25)

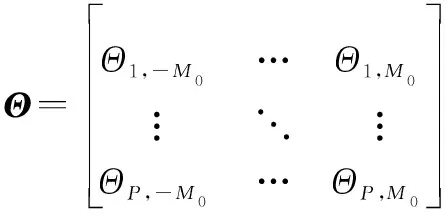
(26)

(27)

則式(24)可以表示為

=

(28)

式中:∈×為包含FRGT系數的系數矩陣;∈×為壓縮感知觀測矩陣;∈×為濾波器輸出矩陣。基于壓縮感知理論,系數矩陣的重構模型為

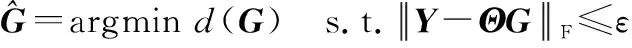
(29)

式中:(·)用來計算矩陣非零行的個數。式(29)可以通過匹配追蹤、稀疏貝葉斯學習等壓縮感知重構算法求解。

3.4 重構誤差分析

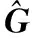
基于壓縮感知理論,系數矩陣的重構誤差可以表示為

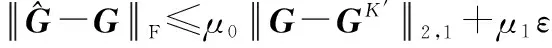
(30)

式中:′為的最佳′行近似;′為系數矩陣的行稀疏度;、為常數。則原始信號的重構誤差可以表示為

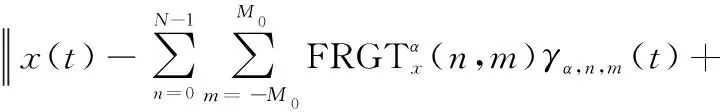
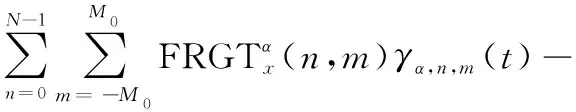
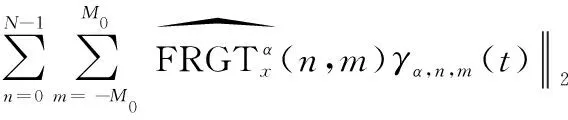
(31)

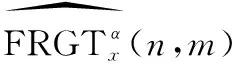
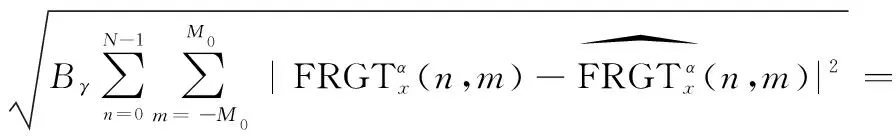
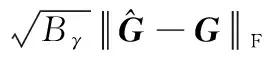
(32)

另一方面,信號的有限展開所造成的誤差可以表示為

(33)

因此原始信號重構誤差可以表示為

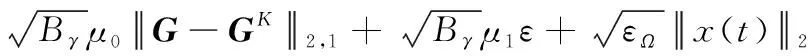
(34)

可以看出,經過壓縮采樣后,原始信號的重構誤差是有界的。

4 實驗與分析

4.1 仿真LFM回波信號

為驗證本文壓縮采樣方法的有效性,進行LFM回波信號仿真實驗。回波信號參數設置如下:載頻=0,調頻率=6 000 MHz/μs,脈沖包絡寬度為01 μs,回波信號總時長=06 μs。回波信號中包含5個回波分量,幅值分別為0.9、0.8、0.7、0.9、0.6,時延分別為0.08 μs、0.2 μs、0.25 μs、0.4 μs、0.44 μs。仿真信號如圖4所示。圖4(a)為信號的時域波形,圖4(b)為仿真信號頻譜,根據信號頻譜特性,實驗中Nyquist采樣頻率設定為2 GHz。圖4(c)為仿真信號分數階頻譜,可以看出,盡管信號在分數階頻域內具有一定的近似稀疏性,但由于泄露效應以及多個回波分量的作用,該稀疏性并不理想。圖4(d)為基于本文所提FRGT的仿真信號時間-分數階頻譜,FRGT參數設置為Δ=0.025 μs,Δcsc=33.3 MHz,=0.074 μs,=120 MHz。可以看出,通過利用各回波分量時延參數的不同,信號在給定時刻的分數階頻譜的稀疏性得到有效改善。

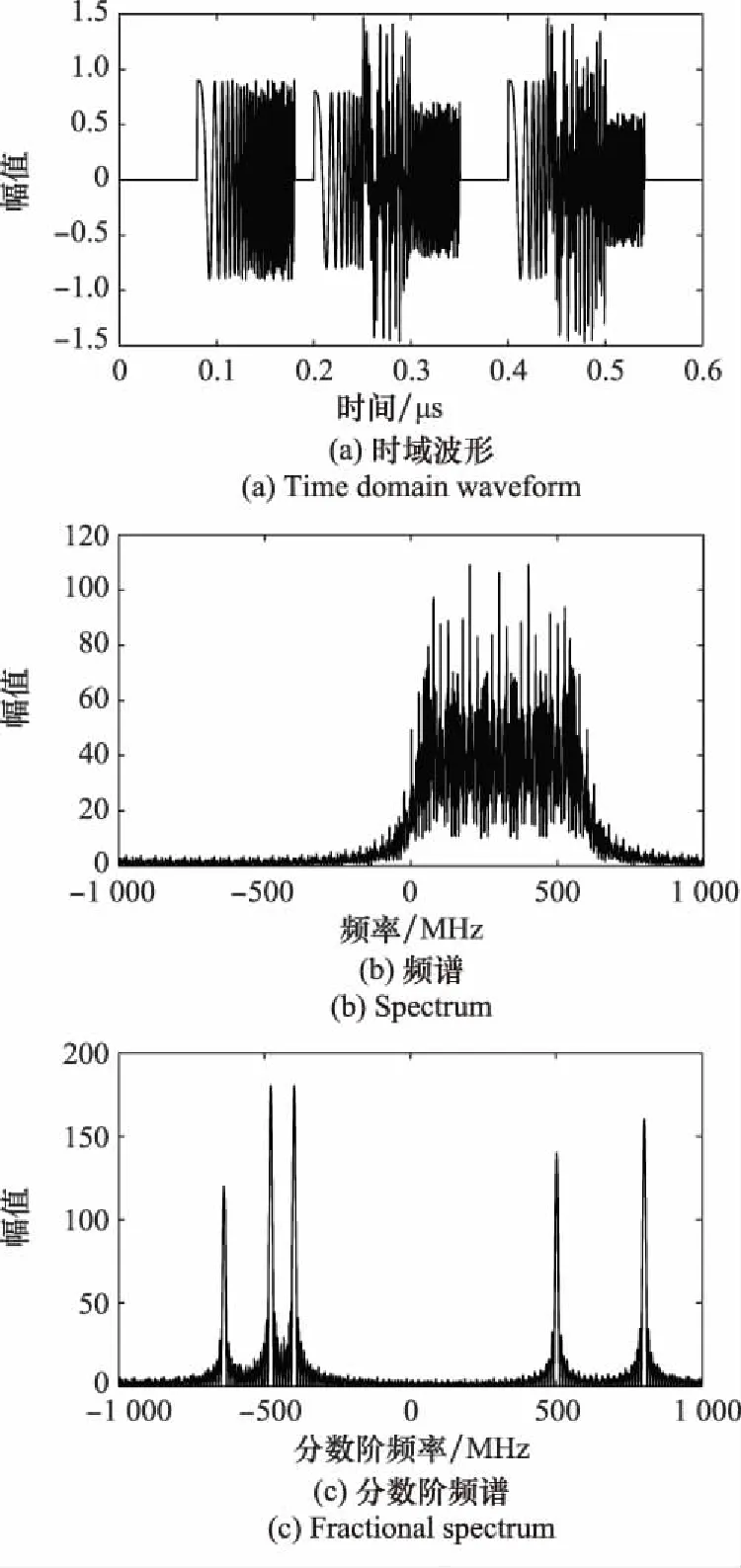
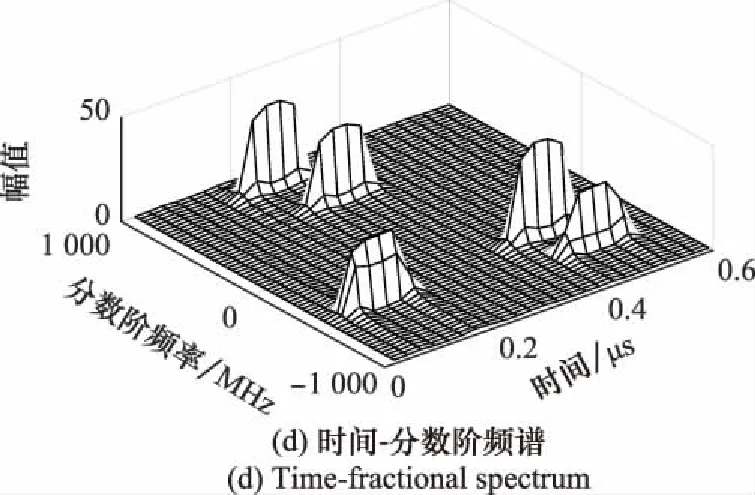
圖4 仿真信號Fig.4 Simulated signals

4.2 壓縮采樣與重構

利用圖3中本文所提的壓縮采樣系統進行壓縮采樣,并完成重構過程。壓縮感知重構算法采用的是文獻[26]中的稀疏貝葉斯學習算法。

實驗過程中分別考慮了采樣通道數以及噪聲對壓縮采樣系統的影響。引入相對誤差(relative error, RE)以衡量系數矩陣的重構效果:

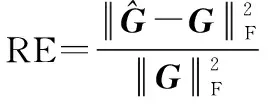
(35)

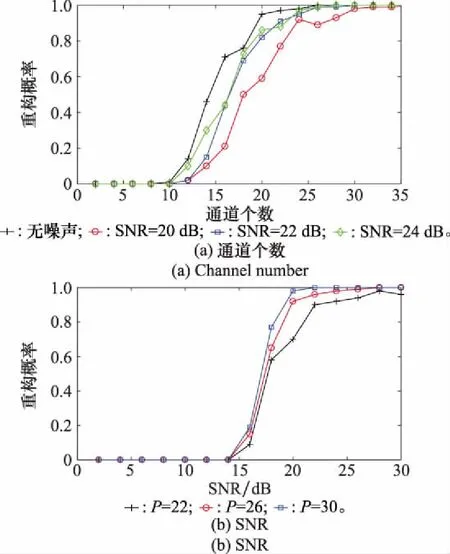
圖5 重構效果Fig.5 Reconstruction effect

從圖5(a)中可以看出,信號系數矩陣的重構概率隨著通道個數的增加而不斷提高,無噪聲條件下,通道個數大于等于20時,重構概率即高于95%。噪聲對重構概率的影響也比較明顯,從圖5(b)中可以看出,當SNR低于14 dB時,重構概率為0,隨著SNR的提升,重構概率不斷提升,并趨近于1。從圖5中可以分析得出如下結論:適當增加采樣通道個數,能夠有效提高壓縮采樣系統的工作穩定性。

為進一步驗證本文壓縮采樣方法的有效性,引入不同的壓縮采樣方法進行對比實驗,不同的壓縮采樣方法如下。

(1) 方法1：文獻[17]中提出的廣義的RD系統;

(2) 方法2：文獻[18]中提出的廣義的MWC系統;

(3) 方法3：本文提出的基于FRGT的壓縮采樣系統。

方法2與方法3均為多通道采樣系統,采樣通道個數設置為26,方法1為單通道系統,設置其總采樣頻率以及總采樣點數與方法2、方法3保持一致。LFM回波信號的分數階頻譜能夠直接反應出多個回波分量的幅值與時延等重要參數信息,因此,重構后的信號均變換到分數階頻域,以分析重構效果。圖6中給出了含噪以及不含噪條件下,不同采樣方法重構后信號的分數階頻譜,含噪條件下,噪聲強度設置為SNR=20 dB。表1則給出了不同方法的壓縮采樣與重構效果對比。實驗過程中,分別計算了重構信號與原始信號之間的RE與局部相對誤差(local RE, LRE)。LRE僅計算5個特征頻率點處的RE。

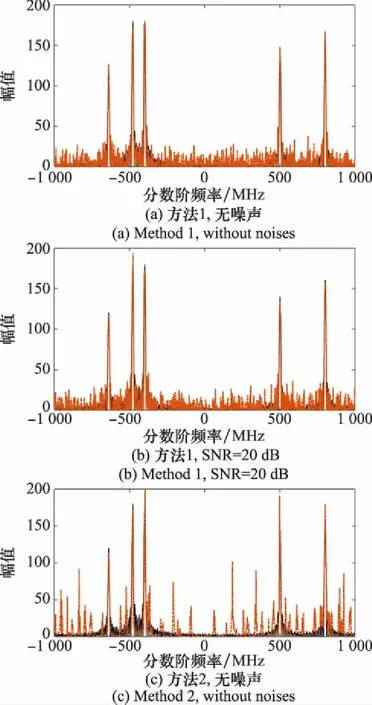
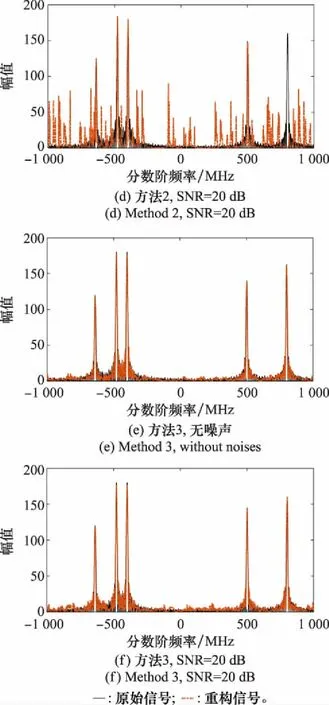
圖6 不同方法重構誤差Fig.6 Reconstruction error with different methods

從表1可以看出,經過壓縮采樣后,信號的總采樣頻率與總采樣點數均遠遠低于Nyquist采樣方法。此時,經過重構后,回波信號在分數階傅里葉變換域的特征頻點得到有效保留。而對比不同采樣方法,可以看出,經過本文所提方法采樣后,信號的重構效果最好,在含噪以及不含噪條件下,RE值與LRE值均低于方法1與方法2。分析其原因,主要是因為本文壓縮采樣方法本質上實現了對信號FRGT系數的壓縮采樣,相比于分數階傅里葉變換,LFM信號在FRGT下具有更好的稀疏性,因此經過壓縮采樣后,信號的重構效果更好。

表1 壓縮采樣與重構效果對比Table 1 Comparison of compressive sampling and reconstruction effect

4.3 應用實例分析

為進一步驗證本文壓縮采樣方法的有效性,選取合成孔徑雷達(synthetic aperture radar, SAR)回波信號作為應用實例,進行SAR回波信號的壓縮采樣與重構數值分析實驗。SAR回波信號是一種典型的LFM回波信號。本文采用了RADARSAT-1實測數據中的一個場景來驗證本文壓縮采樣方法的有效性,場景為加拿大溫哥華的一處港灣,停靠有6艘貨輪。實測數據相關參數如表2所示。

表2 RADARSAT-1 實測數據參數Table 2 Parameters for real RADARSAT-1 data

設定距離向與方位向的總采樣時間分別為21.66 μs、0.795 6 s。則該場景實測數據維度為700×1 000。實測數據如圖7所示,圖7(b)、圖7(c)則分別給出了方位向200處的回波信號波形與分數階頻譜。

圖7 實測數據Fig.7 Real data

本文壓縮采樣系統中,Δ=1.083 μs,則單通道采樣頻率為0.923 4 MHz,采樣點數為20。設定采樣通道個數為20,則總采樣頻率為18.468 MHz,總采樣點數為400。設定方法1、方法2與本文壓縮采樣系統具有相同的總采樣頻率與總采樣點數。對于方位向200處的回波信號,不同采樣方法下重構信號的分數階頻譜如圖8所示。從圖7(b)中可以看出,實測數據中包含有大量的源噪聲以及量化誤差,因此仿真實驗中采用的相對誤差難以有效衡量重構效果。為此本文引入了特征權值(feature weight, FW)如下:

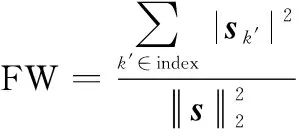
(36)

式中:為信號在分數階傅里葉變換下的系數向量;′為中的特征頻率系數。根據圖7(c),選取[-13.53 MHz,-12.88 MHz]以及[-7.76 MHz,-7.53 MHz],分數階頻段范圍內的系數為特征頻率系數。則不同采樣系統在含噪以及不含噪條件下的重構信號分數階頻譜與FW值如圖8所示,其中,無噪聲條件下,方法1的FW=0.476 1,方法2的FW=0.441 3,方法3的FW=0.580 4,含噪條件下添加的噪聲強度為SNR=20 dB,方法1的FW=0.412 5,方法2的FW=0.379 7,方法3的FW=0.539 0。FW值越大,則重構信號中有用的回波分量比重越大,成像效果越好。探測場景中不同目標距離上的差異導致回波信號具有不同的時延,此時,信號在FRGT下的稀疏性更好,因此本文壓縮采樣方法在含噪或不含噪條件下重構效果均為最佳,FW值最大。

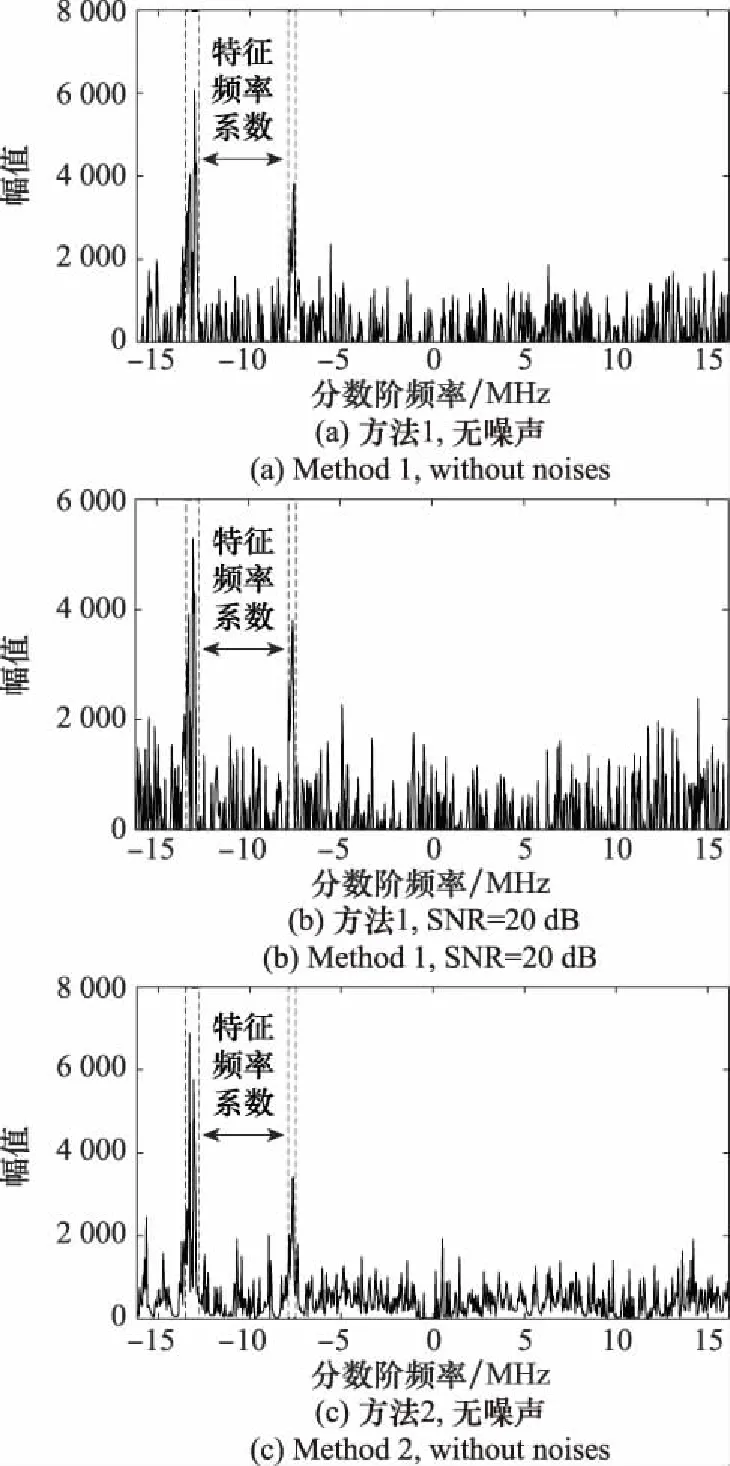
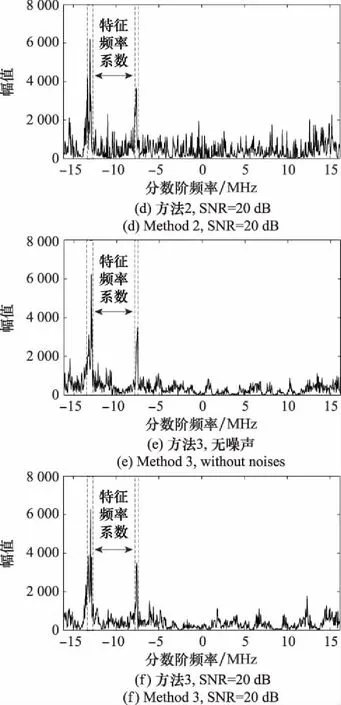
圖8 重構信號分數階頻譜Fig.8 Fractional spectrum for reconstructed signals

對每個方位向信號完成重構后,利用距離多普勒算法進行成像,為進一步量化成像效果,引入圖像熵以及圖像對比度:

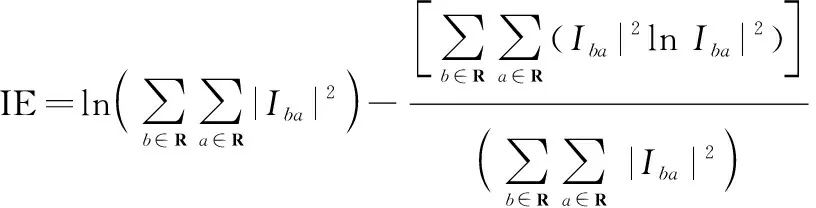
(37)

(38)

式中:=()∈,∈表示圖像;mean(·)為均值算子。圖像熵越小、圖像對比度越高,則成像質量越好。則不同采樣方法下的重構效果如圖9所示,無噪聲條件下,方法1 IE=10.597 1,IC=1.147 3,方法2 IE=10.818 1,IC=1.077 2,方法3 IE=8.788 6,IC=1.850 6,SNR=20 dB條件下,方法1 IE=10.782 8,IC=1.093 3,方法2 IE=11.009 8,IC=1.024 9,方法3 IE=9.528 3,IC=1.505 0。

從圖9中成像效果可以看出,經過本文所提壓縮方法重構后的信號成像效果最好,在含噪以及不含噪條件下,IE值低于方法1與方法2, IC值高于方法1與方法2。本文壓縮采樣系統更有利于保留回波信號中的有用信息,因此成像后IE值更小,IC值更高。另一方面,可以看出,由于壓縮采樣重構過程中存在的誤差,使得重構信號的方位向調頻特性一定程度上被破壞。此時,圖像中的目標沿方位向產生了一定的模糊。如何協調回波信號重構與成像之間的關系,以使信號重構算法與成像算法相適應,需要進一步的研究。

圖9 成像效果對比Fig.9 Comparison of imaging results

5 結 論

本文提出了一種基于FRGT的LFM回波信號壓縮采樣方法。該方法能夠有效利用回波信號中不同回波分量在時延上的差異性,改善信號的壓縮采樣重構效果。針對壓縮采樣系統的實現問題,本文提出了一種新的FRGT實現方法。在系統分析了FRGT的完備性、濾波器結構以及信號有限展開等問題的基礎上,給出了壓縮采樣系統實現方式。本文分析了壓縮采樣系統工作過程并建立了信號的重構模型。通過仿真以及應用實例分析,驗證了本文壓縮采樣系統的有效性。