基于交互多模型的分組δ-廣義標簽多伯努利算法

辛懷聲, 曹 晨

(中國電子科技集團公司電子科學研究院, 北京 100041)

0 引 言

在多目標跟蹤(multiple target tracking, MTT)技術的發展過程中,以數據關聯算法為核心的方法是一類經典技術路線,代表算法有最近鄰關聯、概率數據關聯、聯合概率數據關聯、多假設跟蹤。此類方法的本質是通過數據關聯將MTT問題分解為單目標跟蹤問題。目前這類算法已經在雷達跟蹤系統中得到了應用。

近年來以有限集統計為基礎發展起來了另一類MTT理論。在該理論框架下目標狀態和傳感器量測都由隨機有限集(random finite set, RFS)進行描述建模,并構建最優多目標貝葉斯濾波器,為MTT問題提供了嚴謹、統一、堅實的理論基礎。這類算法的代表有概率假設密度(probability hypothesis density,PHD)、集勢PHD(cardinalized PHD, CPHD)以及CBMeMBer(cardinality balanced multiple target multi-Bernoulli)濾波器。基本PHD、CPHD和CBMeMBer適用于點跡過濾,多目標狀態不包括標簽,不做航跡跟蹤。優勢是計算復雜度較低,以PHD為例計算復雜度僅為()。文獻[11-12]在隨機有限集理論的基礎上,結合數據關聯思想給出了多目標貝葉斯濾波器的精確閉式解,也稱為Vo-Vo濾波器及其δ-廣義標簽多伯努利(δ-generalized labeled multi-Bernoulli,δ-GLMB)版。GLMB濾波器是第一個可以被證明的多目標最優貝葉斯濾波器。

為了提高GLMB濾波器的計算效率,文獻[13]提出標簽多伯努利(labeled multi-Bernoulli,LMB)濾波器,LMB作為δ-GLMB的一種近似解,將分組計算思想引入了GLMB濾波器領域,大幅提高了δ-GLMB的計算效率,但是目標跟蹤精度稍遜于標準δ-GLMB濾波器。為了提高GLMB的航跡跟蹤精度,文獻[14]利用威沙特分布近似處理量測協方差矩陣。文獻[15-16]引入改進型卡爾曼濾波以提高濾波器在非線性情況下的適應度。文獻[17]則改進自適應新生目標航跡起始方法,提高算法的目標數量估計精度。文獻[18-19]將馬爾可夫跳變系統(jump Markov system,JMS)引入GLMB領域,給出JMS-GLMB或多模型Vo-Vo(multi-model Vo-Vo, MM-Vo-Vo)濾波器,提高了GLMB對機動目標的跟蹤精度。文獻[20]則給出了LMB版本的多模型機動目標跟蹤濾波器。然而上述算法都沒有將分組計算和JMS相結合,本文在δ-GLMB濾波器的基礎上結合航跡分組思想對多目標狀態集合和觀測集合進行分組化處理,另外引入JMS對目標狀態進行擴展,參照交互多模型(interacting multiple model,IMM)近似算法給出基于IMM的分組δ-GLMB(IMM based grouping δ-GLMB, IMMG-δ-GLMB)濾波器的預測和更新遞推方程。

文章的第1節介紹基本GLMB算法。第2節給出針對目標狀態和觀測的分組方法,對影響分組的因素進行分析,之后引入JMS對多目標狀態進行擴展,并根據IMM算法對JMS-GLMB進行近似處理,推導出IMMG-δ-GLMB的預測和更新遞推方程以及高斯混合實現方式。第3節設定兩組仿真實驗,第一組實驗設定一個常見的多目標場景,對IMMG-δ-GLMB、δ-GLMB以及JMS-GLMB的MTT性能進行對比,第二組實驗則設定一個密集編隊場景,對不同分組條件下IMMG-δ-GLMB跟蹤密集多目標時的分組濾波效果進行比較分析。第4節進行評價和總結。

1 δ-GLMB濾波算法

本文符號定義采用Mahler在文獻[7]中的定義方式:

定義航跡集合為={(,),(,),…,(,)},||=,其中～分別表示航跡標簽,用于標識不同的航跡身份。

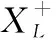
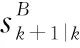
定義(,)為目標存活概率密度函數。

定義|(-|)為均值為|,協方差矩陣為|的多維高斯分布密度函數。

定義量測集合為={,,…,}。～表示傳感器獲取的目標量測。

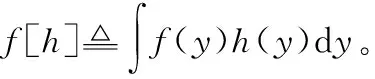
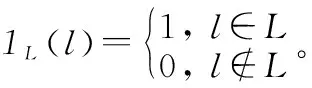
1.1 δ-GLMB濾波器的時間預測

給定時刻多目標狀態的先驗分布密度函數為

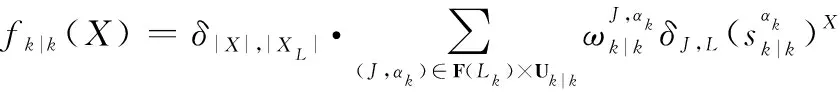
(1)

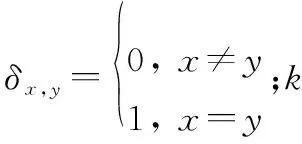
預測步驟的表達式如下所示:

(2)

式中:

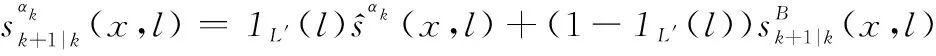
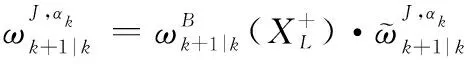
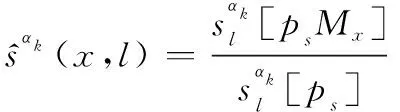
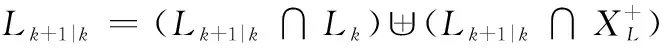
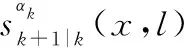
1.2 δ-GLMB濾波器的量測更新

考慮標準點目標量測模型,每一個目標以概率(,)被探測到,被探測到后生成一個量測點,對應的量測似然度表示為(|,)。量測集中不僅有目標形成的量測點,還包括雜波點(虛警點),虛警點構成一個泊松RFS,強度函數為()。在上述假設下,量測更新步驟后生成的后驗密度仍然是δ-GLMB。

給定+1時刻量測集合為+1,相應的多目標后驗分布可以表示為

+1|+1(|+1)=||,||·

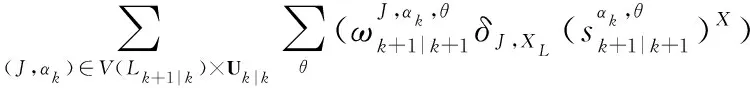
(3)

式中:

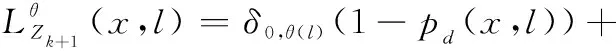
(1-0,())(,)×+1(()|(,))(())

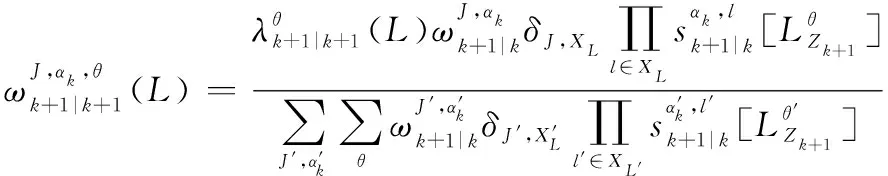
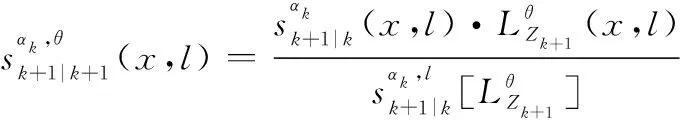
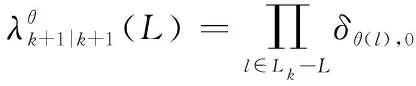
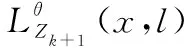
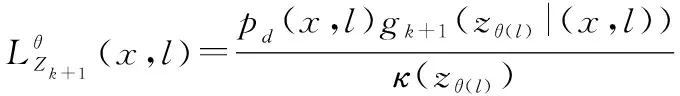
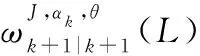
2 IMMG-δ-GLMB濾波算法

本節首先給出航跡與量測的分組方法,之后基于IMM計算框架推導IMMG-δ-GLMB算法的預測和更新表達式。

2.1 航跡與觀測分組

航跡與量測關聯新息可以表示為

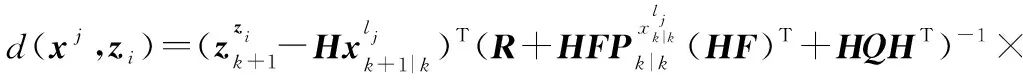
(4)

式中:為狀態轉移矩陣;為觀測矩陣;為狀態轉移過程噪聲矩陣;為觀測協方差矩陣。記矩陣:

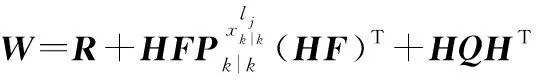
則新息可以重新寫為

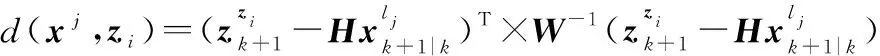
(5)

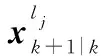
對于一個隨機有限集來說,如果?,∈,使得()=()>0,且≠,根據關聯函數的定義有(,)<且(,)的航跡與標簽為的航跡都可以與同一個量測關聯,此時認為航跡與屬于同一個航跡組,則量測屬于航跡組對應的觀測集合,稱量測可以與航跡組關聯。任何航跡都具有自己所屬的航跡組,不存在一條航跡同時屬于多個航跡組的情況。于是多目標隨機有限集可以劃分為多個航跡組,表示為多個航跡分組的互斥并集。

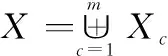
(6)

式中:為航跡組,且∩=?,≠。另外,定義函數的逆函數形式如下:

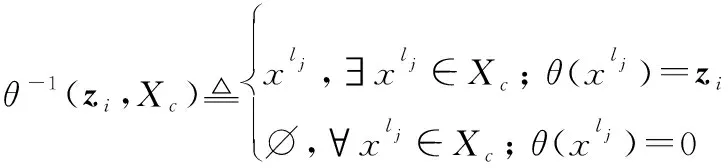
(7)

假設對于兩個航跡組和,如果存在某個量測與兩個航跡組分別能夠關聯,即

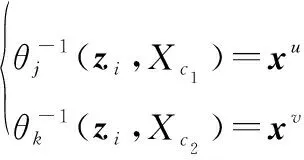
且

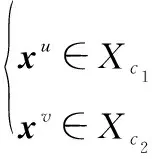
也就是說航跡組和存在共享觀測,則航跡組和可以合并為一個航跡組,即=∪,且觀測集合也可以對應合并,即

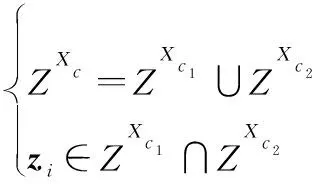
(8)

最后,觀察矩陣的表達式可知航跡組的劃分與目標距離、方位和俯仰誤差、掃描周期以及馬爾可夫運動模型參數有關。通過調整參數組合使得||越小,則對應的,就越大,這樣不同航跡關聯同一量測的可能就越小,航跡組劃分越精細,航跡組數量越多。反之,則航跡組劃分越粗糙,航跡組數量越少。因此可以預計兩種極限情況,第一種極限情況下,每一個航跡組內只包含一個目標,此時分組δ-GLMB(grouping-δ-GLMB, G-δ-GLMB)會轉化為單假設跟蹤(single hypothesis tracking, SHT),此時每個航跡組內的唯一目標要么只能與一個量測關聯,要么沒有量測與之關聯,航跡組的每次時間預測迭代能夠產生的分支也只能有兩條,即目標下一周期繼續存在或者不存在兩種情況。第二種極限情況是所有目標都處于一個航跡組,此時G-δ-GLMB退化為普通δ-GLMB。

2.2 IMMG-δ-GLMB時間預測

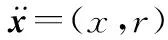
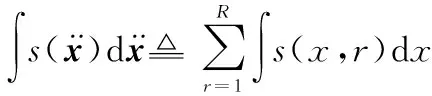
(9)

另外,給定馬爾可夫模式跳變概率矩陣為

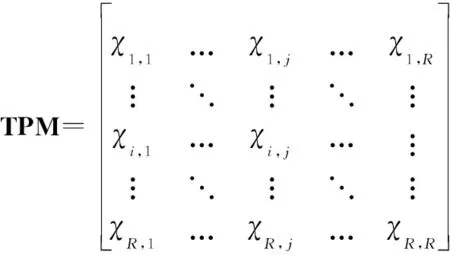
(10)

式中:, 表示模式跳變到模式的概率。對馬爾可夫狀態轉移密度函數使用條件概率規則可以得到馬爾可夫跳變狀態轉移函數:

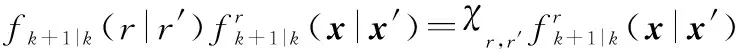
(11)

另外,根據全概率公式,目標的狀態分布可以寫為

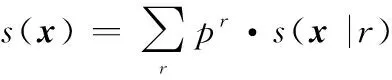
(12)

式中:為目標處于模式的概率。由于不同航跡組之間相互獨立,所以分組多目標分布的先驗分布可以表示為

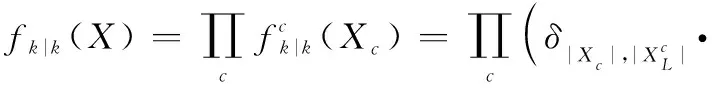
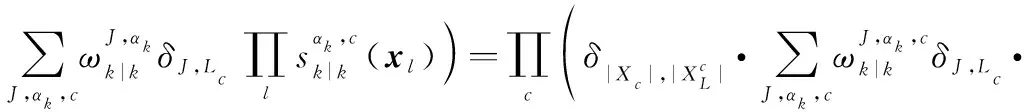
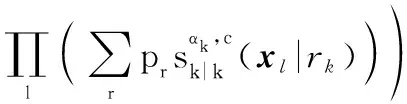
(13)

式中:為分組索引。

根據IMM的狀態分布混合方程有:

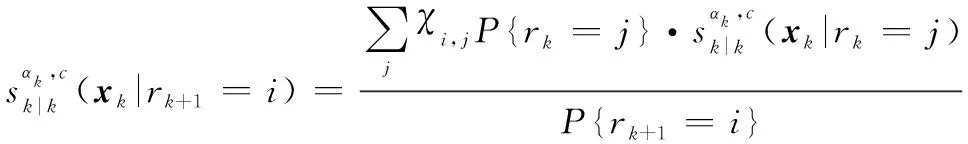
(14)

則經過狀態混合后的多目標分布為

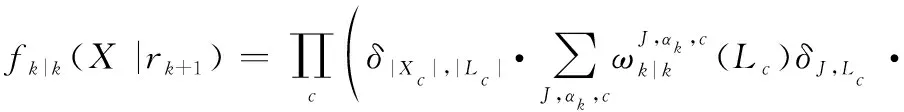
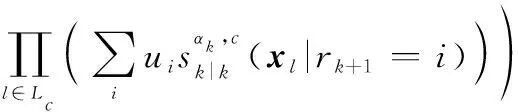
(15)

式中：

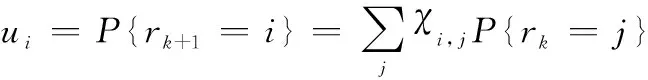
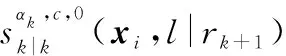
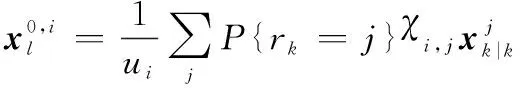
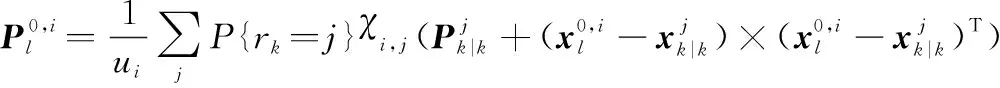
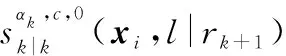
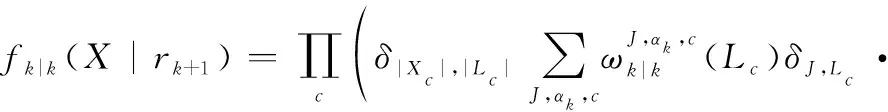
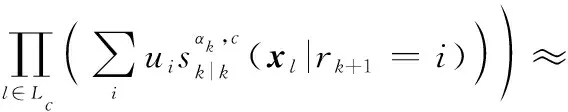
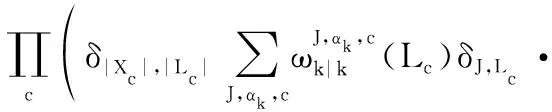
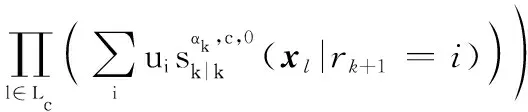
(16)

對經過狀態混合后的多目標分布式(16)進行時間預測,得到的多目標時間預測分布密度函數可寫為

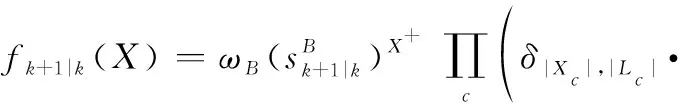
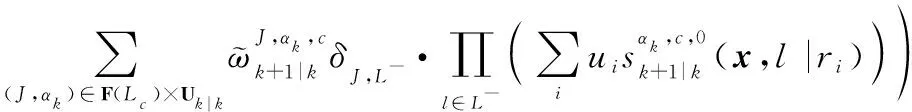
(17)

式中：

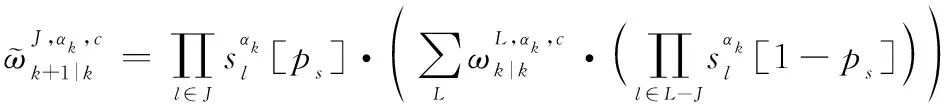
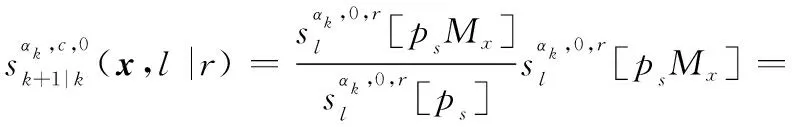
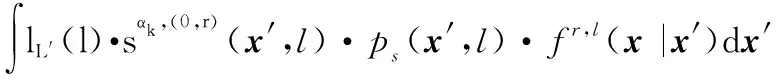
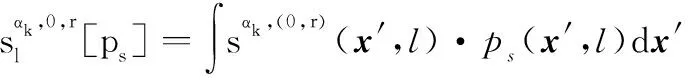
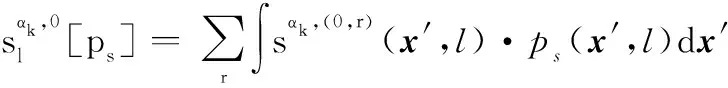
2.3 IMMG-δ-GLMB的量測更新

經過觀測濾波后,多目標后驗分布仍然可以表示為各個航跡組GLMB分布的乘積,保證濾波迭代的封閉:

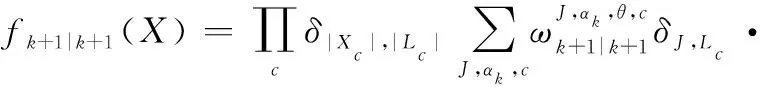
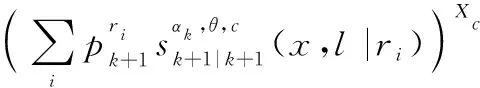
(18)

式中:

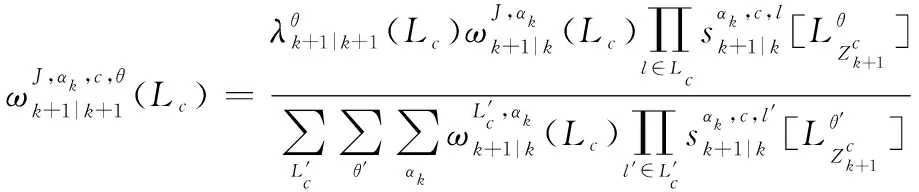
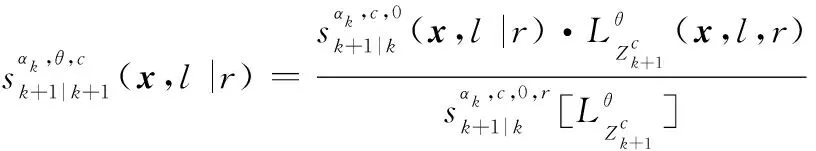
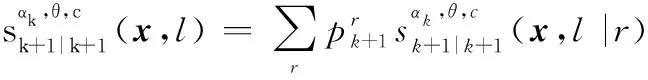
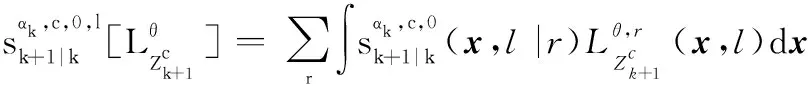
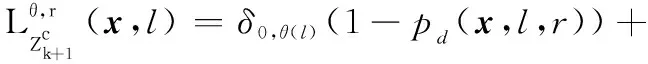
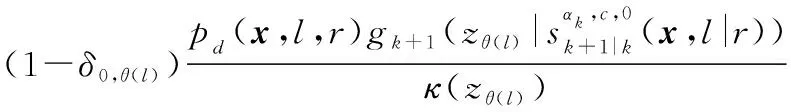
IMMG-δ-GLMB的模式概率更新方程如下:

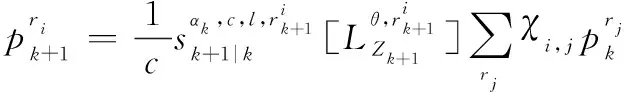
(19)

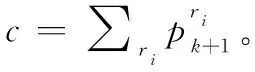
2.4 IMMG-δ-GLMB的高斯混合實現

在假設目標新生模型、運動模型、觀測模型都滿足線性高斯條件,并且目標存活概率和目標探測概率都是常數后,可以得到IMMG-δ-GLMB的高斯混合遞推公式。

根據式(17),多目標時間預測分布密度函數可寫為

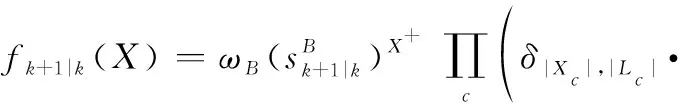
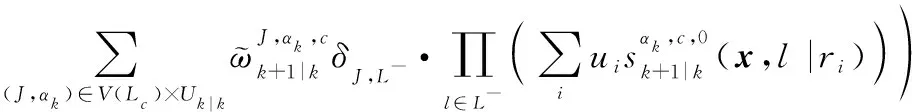
則在線性高斯條件可以得到

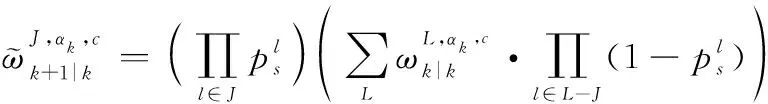
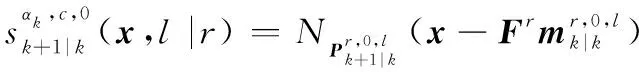
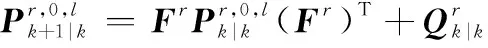
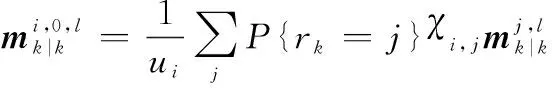
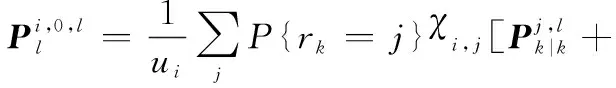
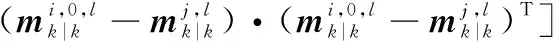
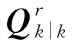
按照式(18),觀測更新可以寫為

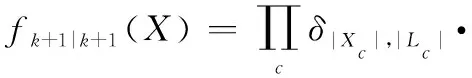
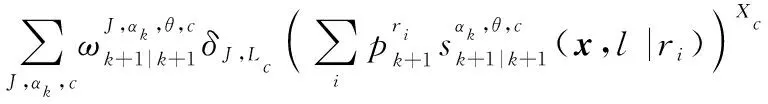
則在線性高斯條件下有

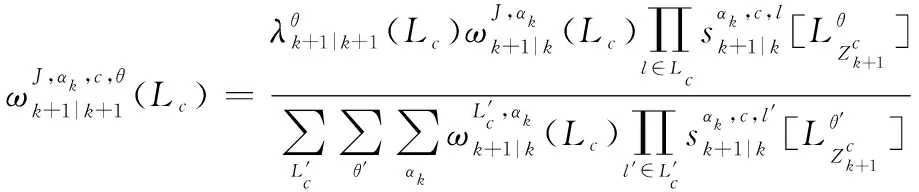
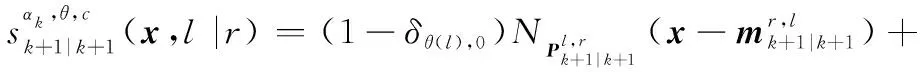
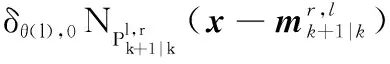
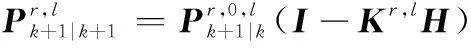
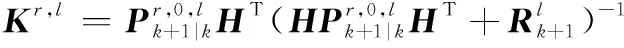
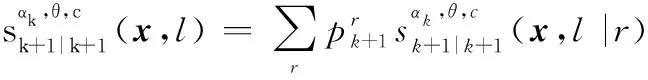
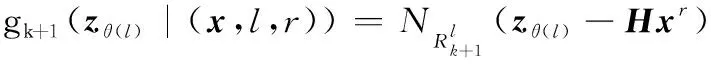
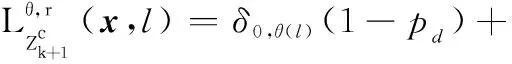
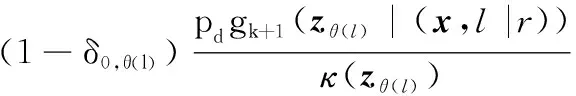
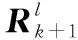
觀測更新后目標狀態提取方程為

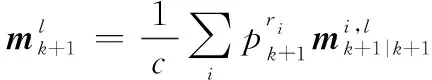
(20)

對應的協方差矩陣為

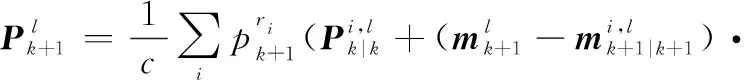
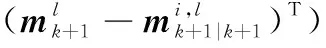
(21)

根據式(19),線性高斯條件下IMMG-δ-GLMB的模式概率更新方程如下:

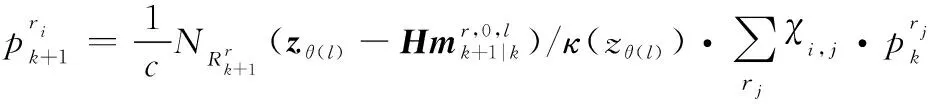
(22)

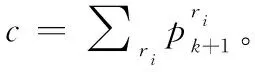
3 仿真與結果分析

3.1 仿真場景1

設置一個兩維跟蹤場景,比較δ-GLMB、JMS-GLMB和IMMG-δ-GLMB的MTT性能。仿真場景設置如下:傳感器至于坐標原點(0,0)m,傳感器量測周期=8 s。觀測區域設置為[0,150 000] m×[-20 000,100 000] m,IMM和JMS的運動模型集均由一個勻速運動模型CV、一個右轉模型CT(5°/s轉彎速率的協同轉彎模型)和一個左轉模型CT(-5°/s轉彎速率的協同轉彎模型)組成。

CV的運動方程如下:

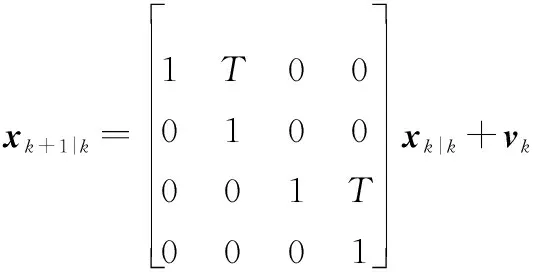
右轉模型CT(=5π180)的運動方程如下:

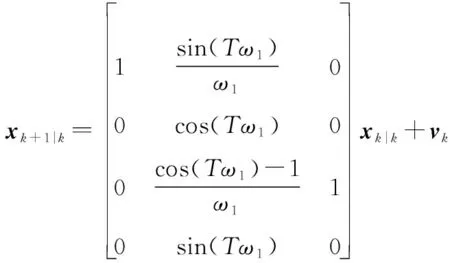
左轉模型CT(=-5π180)的運動方程如下：

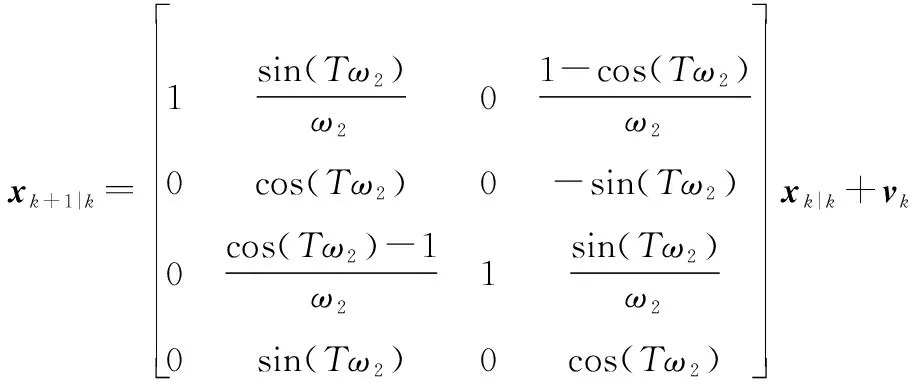
過程噪聲協方差矩陣:

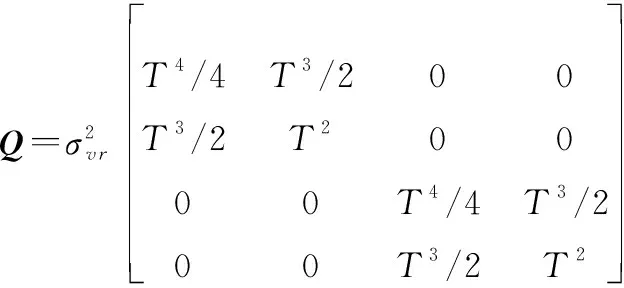
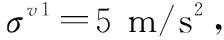
馬爾可夫狀態轉移概率矩陣給定如下:

為了一定程度上適應目標的機動,為標準δ-GLMB選取的運動模型,為辛格模型。運動方程如下:

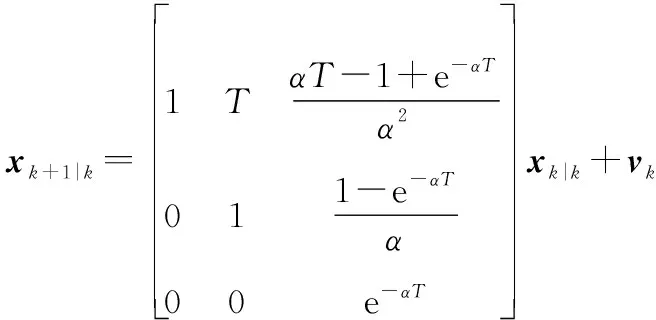
過程噪聲矩陣:

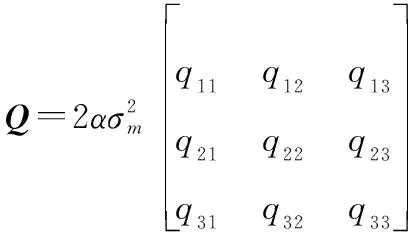
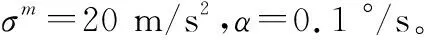
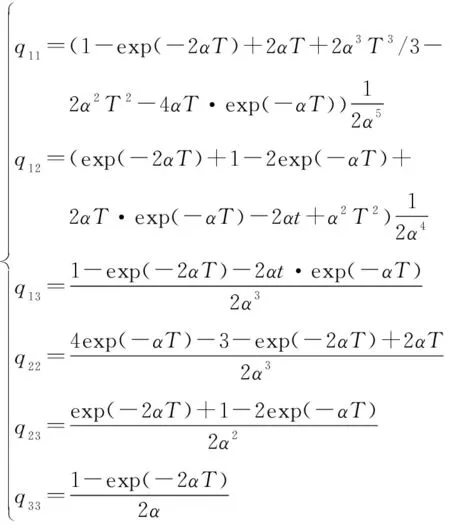
目標的存活概率設為099。目標的初始狀態設置如表1所示。

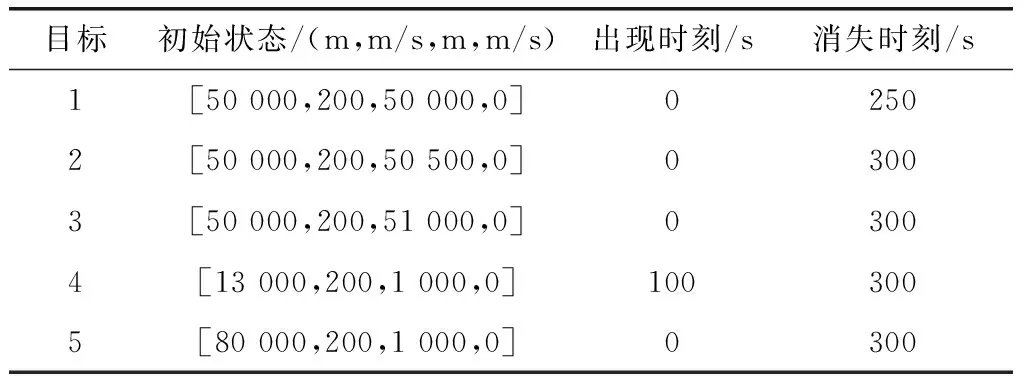
表1 目標初始狀態Table 1 Initial states of all targets

仿真開始后,目標1、目標2、目標3和目標5出現。其中,目標1～目標3按照CV模型運動,目標5按照CT(2 °/s左轉)模型運動。在100～110 s之間,目標3轉換為CT(5 °/s右轉)模型運動,之后恢復為CV模型。目標4在100 s時刻出現在坐標(130 000,1 000)。在100～120 s之間，目標4按照CT(5 °/s左轉)模型運動,120～140 s目標4恢復為CV模型,140～150 s之間目標4按照CT(5 °/s左轉)模型運動,之后恢復為CV模型。160～200 s之間目標1和目標2按照CT(2 °/s右轉)模型運動,目標3在150～250 s之間按照CT(2 °/s右轉)模型運動,之后恢復CV模型運動。目標1在250 s時刻消失,至300 s時刻仿真停止。各目標運動模型轉換的時序如圖1所示。

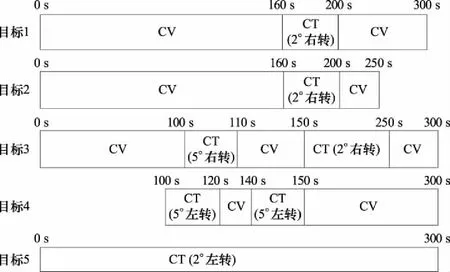
圖1 目標運動模型轉換時序圖Fig.1 Target motion model jumping sequence

目標的真實運動路徑如圖2所示。

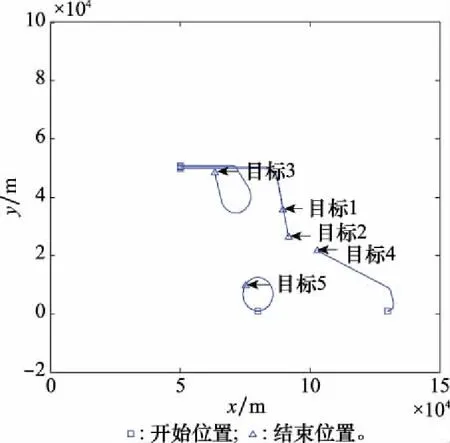
圖2 目標運動軌跡Fig.2 Targets’ motion trajectories

由于標準GLMB采取的已知新生目標分布的策略,無法對中斷的航跡重新起始,所以本文在3種濾波器性能比較中都加入了自適應的航跡起始算法。

為了降低雜波對數據關聯的影響,3種算法都采用多普勒量測信息驗證關聯量測點。處于跟蹤波門內的多普勒量測誤差過大的量測點會被濾除。多普勒信息似然度表達式為

(,+1|+1)=N(,+1;(+1),,)

(23)

式中:,+1為目標多普勒量測;,為多普勒量測方差;(+1)為多普勒觀測方程。

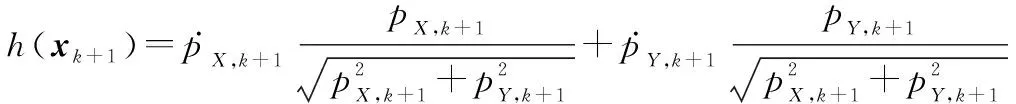
(24)

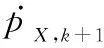
3種濾波算法的量測方程采用極坐標形式，如下所示：

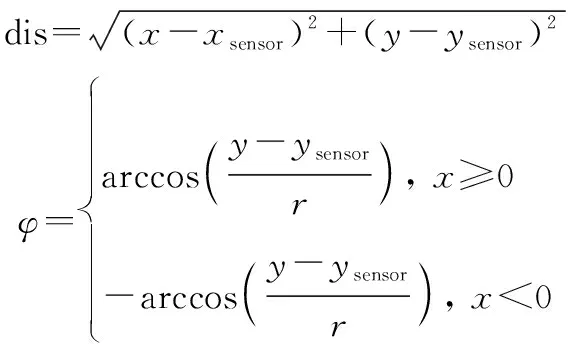
式中：dis為目標距離;為目標方位角;為傳感器的軸坐標；為傳感器的軸坐標。

量測協方差矩陣設置如下:

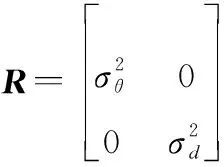
(25)

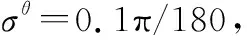
每個掃描周期的雜波點數服從均值的泊松分布,每個雜波點在觀測范圍內均勻分布。誤差評估計算最優子模式分配(optimal sub-patten assignment, OSPA)的參數設定為=1,=1 000 m。

對δ-GLMB、JMS-GLMB和IMMG-δ-GLMB算法分別進行100次蒙特卡羅實驗。探測概率取0.95,雜波率取10的情況下,航跡跟蹤精度對比如圖3所示。OSPA曲線的兩個峰值出現位置吻合100 s時刻發生目標新生和250 s時刻發生目標消亡。

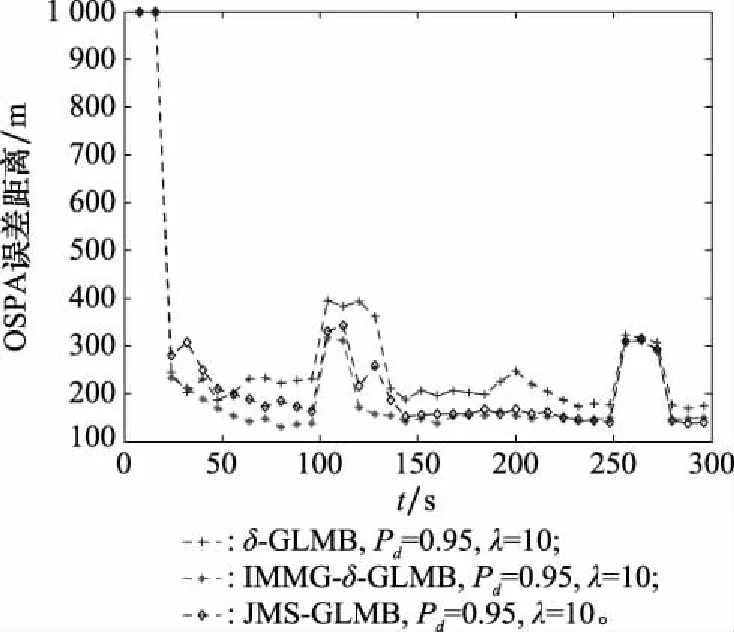
圖3 3種算法跟蹤精度對比Fig.3 Tracking accuracy comparison of three algorithms

為了驗證不同探測概率對IMMG-δ-GLMB的影響,在雜波率取20,探測概率分別取0.95、0.85和0.75的3種情況下,進行50次蒙特卡羅實驗, OSPA誤差曲線如圖4所示。

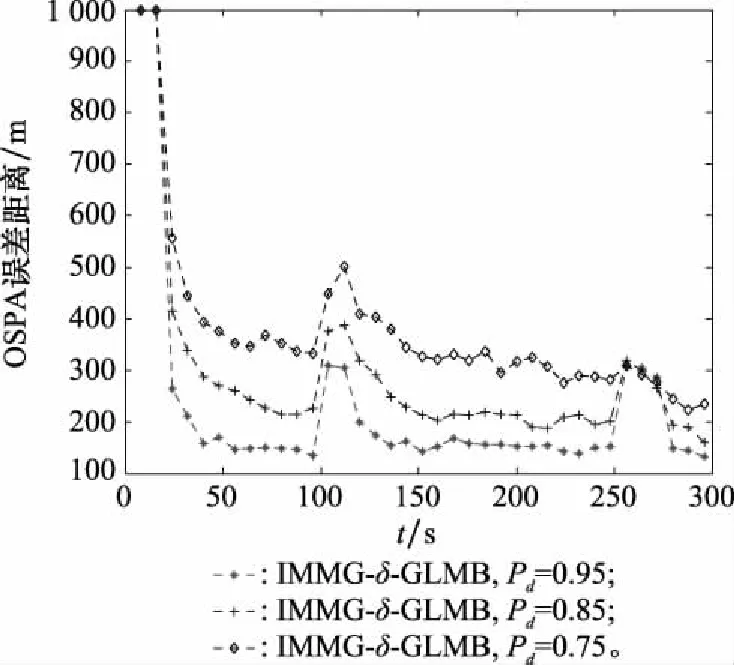
圖4 探測概率對IMMG-δ-GLMB跟蹤精度的影響Fig.4 Influence of detection probability on IMMG-δ-GLMB tracking accuracy

為了驗證不同雜波率對IMMG-δ-GLMB的影響,在探測概率取0.95,雜波率分別取10、50和100的3種情況下,進行50次蒙特卡羅實驗,OSPA誤差曲線如圖5所示。

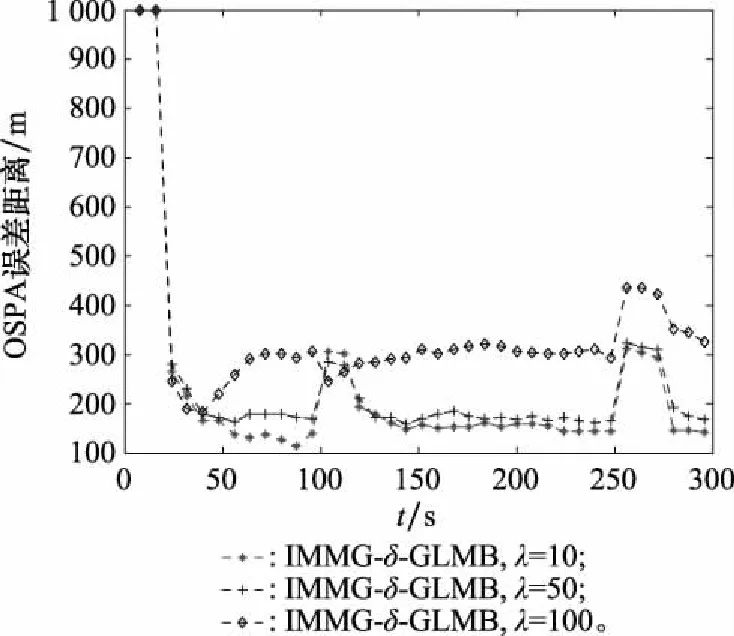
圖5 不同雜波率對IMMG-δ-GLMB跟蹤精度的影響Fig.5 Influence of different clutter ratios on IMMG-δ-GLMB tracking accuracy

最后,為了驗證3種算法的計算復雜度隨目標數量增加而增加的情況,在探測概率取0.95,雜波率取20的設定下,將場景設定的5個目標軌跡加一個隨機的坐標偏移并進行復制，得到10目標、15目標和20目標場景。然后對比5目標、10目標、15目標、20目標4種情況下IMMG-δ-GLMB、JMS-GLMB和基本δ-GLMB濾波器的計算時間，結果如表2所示。

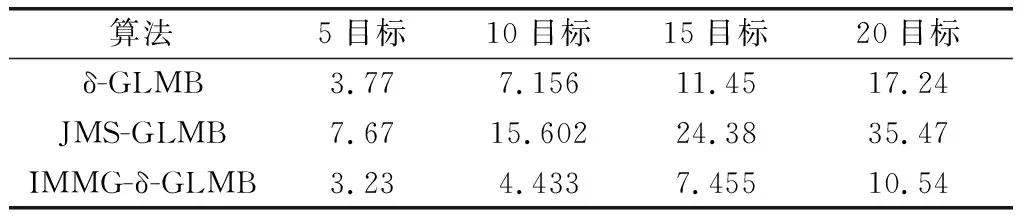
表2 3種算法不同目標數量場景的計算時間結果對比Table 2 Comparison of calculation time results of three algorithms in different target number scenarios s

實驗結果分析如下。

(1) 從圖3可以看出,IMMG-δ-GLMB比JMS-GLMB精度稍高,與δ-GLMB相比跟蹤精度優勢明顯,這是因為一方面IMM與單辛格模型相比能夠更好地適應目標的運動模型變化;另一方面,JMS-GLMB為了控制假設數量,在實際仿真中需要對假設數量進行的剪枝,造成誤差可能超過IMM的現象,如果想要提高JMS-GLMB的精度需要保留更多的假設分支,代價是進一步提高JMS-GLMB的計算復雜度。另外,從表2可以看出,IMMG-δ-GLMB與δ-GLMB和JMS-GLMB相比計算速度更快,主要原因是IMMG-δ-GLMB采用了航跡分組計算。

(2) 從圖4可以看出,IMMG-δ-GLMB的航跡跟蹤精度隨探測概率的下降而下降。這主要由于隨著探測概率的下降,航跡需要更長時間確認起始,另外在跟蹤過程中也更容易出現由于連續沒有量測點導致航跡中斷的問題。

(3) 從圖5 可以看出,IMMG-δ-GLMB的航跡跟蹤精度都隨雜波率的增長而下降。但是在雜波率不高的階段,由于采用了多普勒量測信息抑制雜波點參與航跡起始和關聯,OSPA跟蹤精度的下降不明顯。只有在雜波率高到頻繁出現虛假航跡起始和誤關聯時,OSPA跟蹤精度才會出現比較明顯的下降。

3.2 仿真場景2

為了驗證傳感器掃描周期、傳感器探測精度、目標距離以及運動模型參數對IMMG-δ-GLMB的影響。設定一個多目標密集編隊運動場景,在這個場景中由于目標之間距離較近,可以通過調整影響矩陣的參數測試航跡組數量的變化以及對應的航跡跟蹤精度。

由于量測模型和狀態轉移模型噪聲的存在,密集編隊目標的航跡比較常見航跡交叉現象,為了衡量這類航跡跟蹤誤差,引入標簽OSPA(labeled OSPA, LOSPA)誤差模型,定義如下:

=+

(26)

式中：為航跡交叉次數;為單次航跡交叉引入的誤差懲罰;為OSPA距離。

密集編隊目標運動軌跡設定如圖6所示,橫縱坐標的單位均為m。5個目標間隔1 500 m編隊運動,初始坐標設定為:[0707,0707,1 000]、:[0707,0707+1 500,1 000]、:[0707,0707+3 000,1 000]、:[0707,0707+4 500,1 000]、:[0707,0707+6 000,1 000],單位為m。其中為第一個目標距離傳感器的距離。目標、在0 s時刻出現,、和在20 s時刻出現。

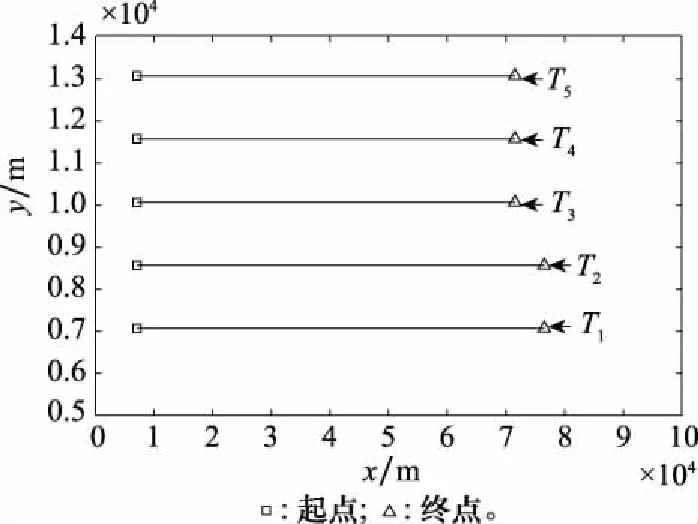
圖6 密集編隊目標運動軌跡Fig.6 Dense formation target trajectory

從表3選取4個參數,在不同的參數搭配下測試密集編隊目標的分組情況和跟蹤精度。例如參數組合[,,,]代表掃描周期1 s,方位標準差0.1°,加速度方差10 m/s,距離100 km的組合。為了消除單次實驗的隨機性,每組參數組合進行50次蒙特卡羅實驗。

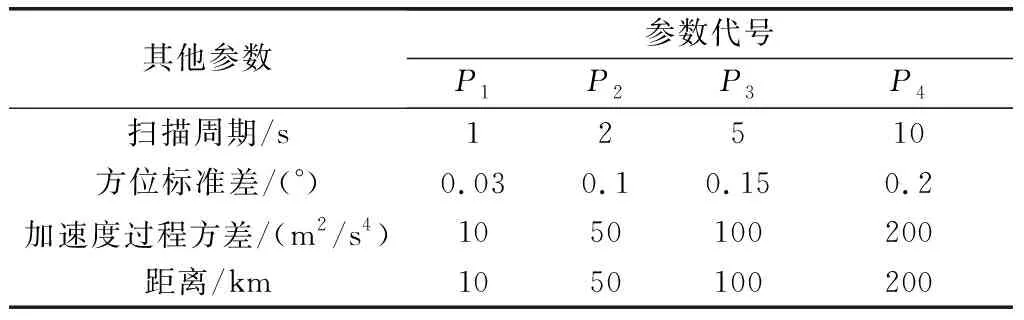
表3 影響分組的參數Table 3 Parameters affecting grouping

參數組合[,,,]情況下,分組數量曲線和LOSPA誤差曲線如圖7所示。LOSPA曲線出現的峰值位于目標、和的航跡起始階段。航跡組的數量在目標、和出現之前約等于2,也就是說目標和分別處于兩個航跡組內,在目標、和的航跡起始后,航跡組數量從2個增加到5個,說明目標、、、和都處于單獨的航跡組內,每個航跡組內只有一條航跡。

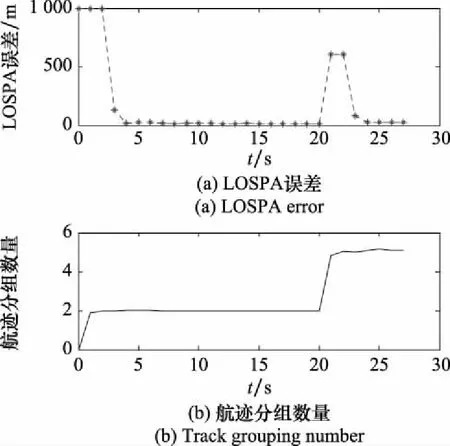
圖7 [P1,P2,P1,P3]參數對應的LOSPA誤差與航跡分組數量曲線Fig.7 Curve of LOSPA error and track grouping number corresponding to parameter [P1,P2,P1,P3]

參數組合[,,,]情況下,分組數量曲線和LOSPA誤差曲線如圖8所示。方位誤差放大到0.2°的情況下,LOSPA略微上升和航跡組數量曲線在5個目標并存的情況下出現波動。

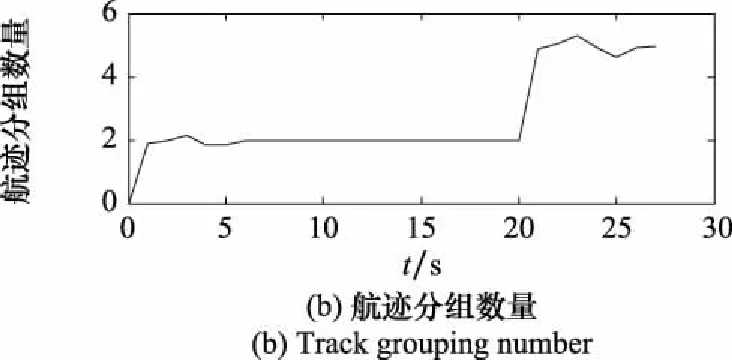
圖8 [P1,P4,P1,P1]參數對應的LOSPA誤差與 航跡分組數量曲線Fig.8 Curve of LOSPA error and track grouping number corresponding to parameter [P1,P4,P1,P1]

參數組合[,,,]情況下,分組數量曲線和LOSPA誤差曲線如圖9所示,LOSPA曲線的第4和第5點較高的原因是目標、和處于航跡起始階段。從航跡組數量可以看出目標和航跡起始階段航跡組數量在1到2之間,目標、和航跡起始階段航跡組數量在3到4之間,5個目標航跡全部起始完畢后,航跡組數量維持在4左右,少于目標總數5。說明出現了兩個目標處于一個航跡組內的情況。

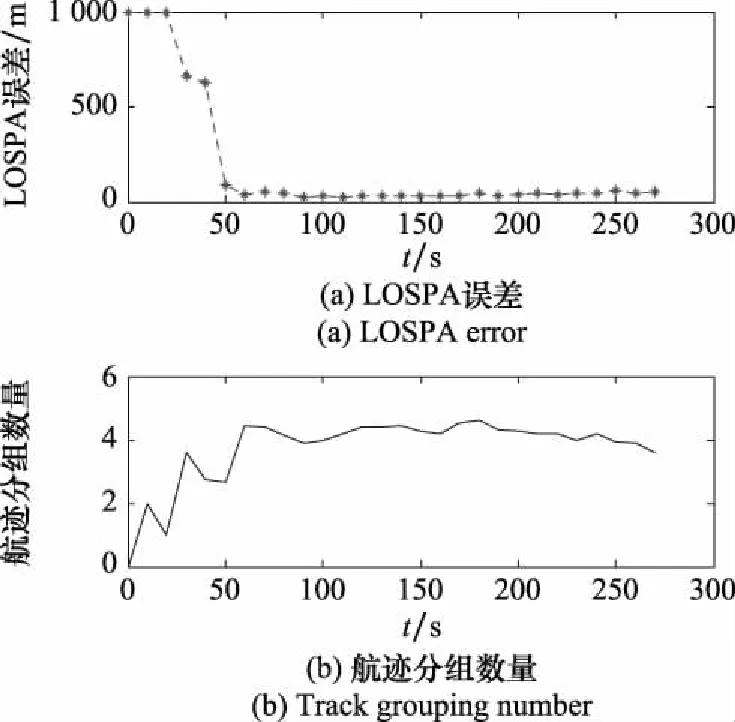
圖9 [P4,P1,P1,P1]參數對應的LOSPA誤差與 航跡分組數量曲線Fig.9 Curve of LOSPA error and track grouping number corresponding to parameter [P4,P1,P1,P1]

參數組合[,,,]的情況下,分組數量曲線和LOSPA誤差曲線如圖10所示。由于傳感器采用極坐標的原因,量測點距離目標實際位置的誤差隨距離的增加而增加,進而導致LOSPA誤差放大,最終導致航跡數量和航跡組數量的波動。

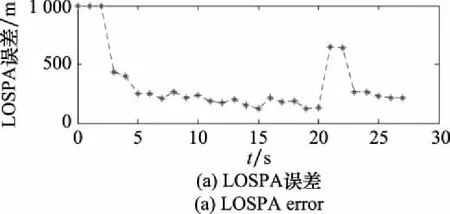
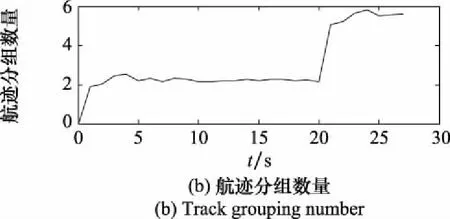
圖10 [P1,P1,P1,P4]參數對應的LOSPA誤差與航跡分組數量曲線Fig.10 Curve of LOSPA error and track grouping number corresponding to parameter [P1,P1,P1,P4]

參數組合[,,,]情況下,分組數量曲線和LOSPA誤差曲線如圖11所示。在放大3個參數后航跡組數量保持在2,目標、合并為一個航跡組,晚20 s出現的目標、和合并為另一個航跡組。

圖11 [P4,P2,P2,P1]參數對應的LOSPA誤差與航跡分組數量曲線Fig.11 Curve of LOSPA error and track grouping number corresponding to parameter [P4,P2,P2,P1]

參數組合[,,,]情況下,分組數量和LOSPA曲線如圖12所示,航跡組數量曲線已經下降到約1.5。

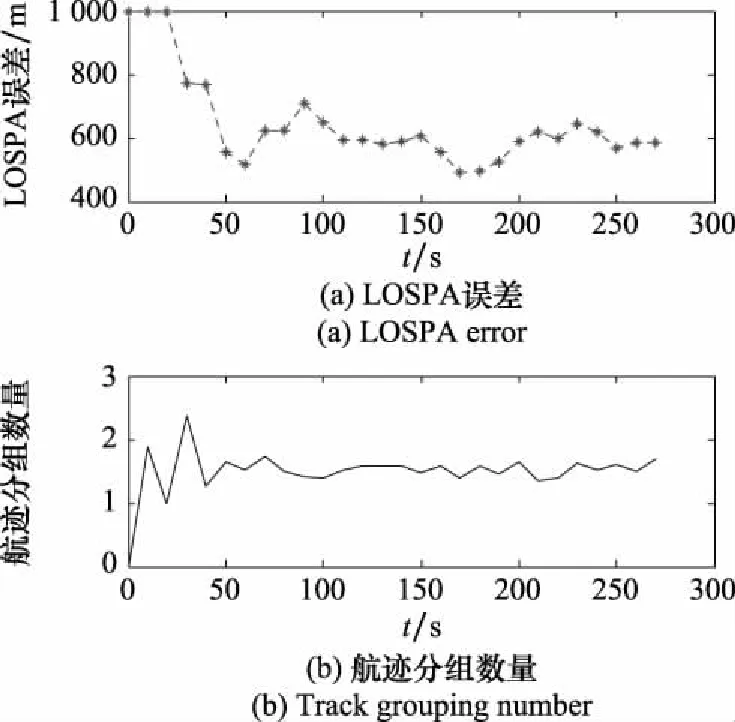
圖12 [P4,P2,P1,P4]參數對應的LOSPA誤差與航跡分組數量曲線Fig.12 Curve of LOSPA error and track grouping number corresponding to parameter [P4,P2,P1,P4]

參數組合[,,,]情況下,分組數量和LOSPA曲線如圖13所示,航跡組數量下降到了1。

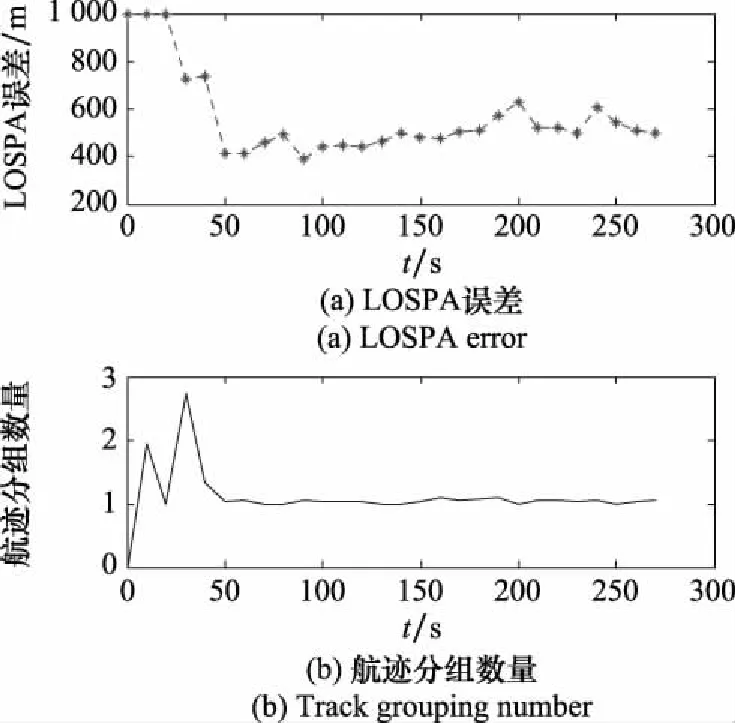
圖13 [P4,P2,P3,P3]參數對應的LOSPA誤差與航跡分組數量曲線Fig.13 Curve of LOSPA error and track grouping number corresponding to parameter [P4,P2,P3,P3]

從上述實驗結果可以看出,高精度、高數據率以及適當的狀態轉移參數可以使IMMG-δ-GLMB有效地識別密集編隊內的獨立目標,使每個目標獨立成組,此時航跡跟蹤精度最高。隨著探測精度和數據率的下降以及狀態轉移矩陣參數調整,IMMG-δ-GLMB分辨目標的能力開始下降,航跡跟蹤精度也隨之下降,分組數量減少,每個分組內的目標數量上升。持續放大探測誤差、數據率并調整狀態轉移矩陣參數,航跡分組數量可以降低到1,此時IMMG-δ-GLMB的濾波迭代過程就退化為IMM-δ-GLMB。值得注意的是,調整狀態轉移模型參數雖然也可以改變分組情況,但是調整不當可能導致運動模型失配,嚴重時會造成目標跟蹤失敗。

4 結 論

本文在δ-GLMB的基礎上引入分組濾波計算思想和IMM計算框架,利用IMM對分組處理后的JMS-GLMB進行運動模式分支合并近似,推導出IMMG-δ-GLMB的迭代方程,并給出高斯混合實現方式。

仿真結果表明,一方面,IMMG-δ-GLMB能夠有效對多目標進行跟蹤,與δ-GLMB和JMS-GLMB相比目標跟蹤精度更高,計算速度更快。 另一方面,IMMG-δ-GLMB的分組情況受傳感器精度、目標距離、掃描數據率以及狀態轉移參數的影響。在狀態轉移參數與目標運動狀態匹配的情況下,高精度、高數據率的量測數據可以增加分組數量,提高算法運行效率和目標跟蹤精度。反之,低精度、低數據率的情況會減少分組數量,極端情況下可能使IMMG-δ-GLMB退化為IMM-δ-GLMB。