基于呂氏分布的機動目標參數化平動補償方法

劉豐愷, 黃大榮,*, 郭新榮, 馮存前

(1. 空軍工程大學防空反導學院, 陜西 西安 710051; 2. 武警工程大學基礎部, 陜西 西安 710086)

0 引 言

克服由目標非合作特性給ISAR成像帶來的影響是提升逆合成孔徑雷達(inverse synthetic aperture radar, ISAR)成像效果的重要途徑。一般而言,目標的運動可以被分解為平行于雷達視線方向的運動和垂直于雷達視線方向的運動,即平動和轉動。而平動補償的目的是消去目標平動對回波的影響,保證ISAR成像的質量。對機動目標進行成像一直是ISAR成像的重點研究方向,目前諸多學者提出了多種具有良好性能的機動目標成像方法,但這些方法主要著眼于解決目標非均勻轉動對ISAR成像的影響,對機動目標平動補償的問題并未深入討論。

傳統的平動補償方法通常分兩步進行,即首先將脈沖壓縮后的回波包絡對齊,然后矯正由平動帶來的相位誤差。其中,包絡對齊對精度要求相對較低且易于實現,一般采用平均距離像相關法就能穩定實現包絡對齊。而相位矯正需要較高的精度,是平動補償的重點和難點。常用的相位矯正方法包括多普勒中心法、特顯點法等。這些方法在目標平穩運動時能夠獲得較好的效果,但當目標機動時,復雜的相位變化會使這些方法難以得到較好的結果。為了提高相位矯正的性能,部分學者提出了一系列基于相位梯度自聚焦(phase gradient autofocus, PGA)的相位矯正方法。PGA能夠有效克服傳統相位矯正方法的不足,但由于PGA需要進行重復的迭代運算,因此需要較大的運算量。事實上,平動對包絡和相位的影響本質上是一致的,因此有學者提出對目標平動進行建模并基于圖像質量估計運動參數,以實現包絡和相位的同時補償,具有一定的借鑒意義。但基于圖像質量估計運動參數在信噪比較低時可能會出現較大的誤差,因此亟待改進。

為了克服現有平動補償方法的不足,實現對機動目標回波信號的準確平動補償,本文提出一種基于呂氏分布(Lv’ s distribution, LVD)的參數化平動補償方法。該方法將含有平動誤差的機動目標回波建模為多項式相位信號,利用相位差分聚焦各距離單元的能量,然后采用LVD估計信號參數,最后利用估計得到的參數構建補償函數,消除平動誤差。實測數據實驗證明了所提方法的有效性和低信噪比條件下的優越性能。

1 信號模型

現代雷達廣泛采用線性調頻信號作為發射信號,可以被表示為

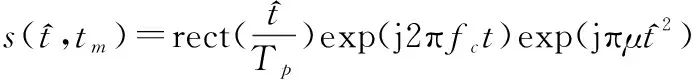
(1)

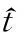
含有平動影響的ISAR成像模型如圖1所示。

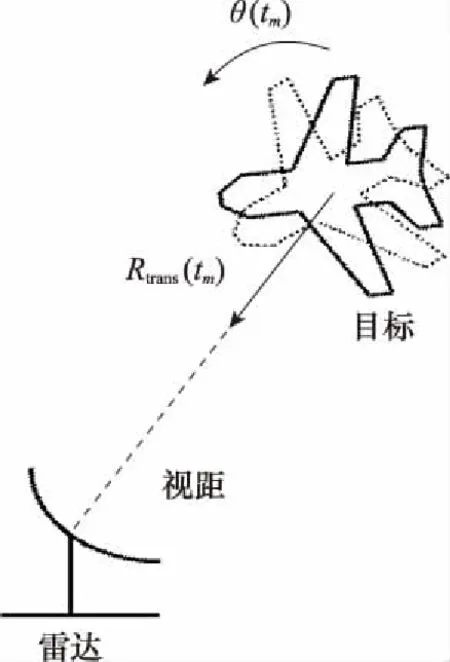
圖1 含有平動影響的ISAR成像模型Fig.1 ISAR imaging model with translational effects

其中,()為目標平動距離;()為目標轉動的總角度。

根據點散射模型,目標可以被認為由多個散射點組成,設發射信號經目標中某一散射點反射形成回波,則目標回波可以表示為

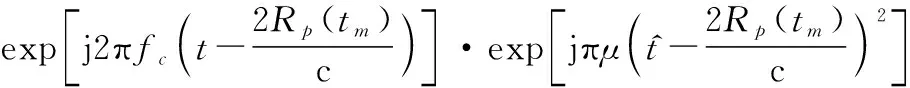
(2)

式中:()為雷達到散射點的距離,根據停跳假設,()僅與有關;c為光速。

寬帶線性調頻信號的脈沖壓縮通常采用解線頻調算法(Dechirp),對式(2)進行Dechirp處理后得到的結果為

(3)

式中:為信號帶寬;為等效慢時間,其表達式為

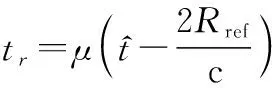
(4)

式中:為參考距離。

式(3)中的Δ()包括平動和轉動兩部分,其可以被寫為

Δ()=()+cos(())+sin(())

(5)

式中:為散射點相對于目標中心的徑向距離;為散射點相對于目標中心的橫向距離。根據文獻[1]和文獻[28],()和()可以表示為

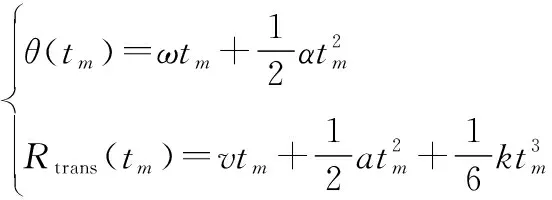
(6)

式中:為轉動速度;轉動加速度;為平動速度;為平動加速度;為二階平動加速度。考慮到在ISAR成像過程中,目標轉動的總角度通常較小,采用泰勒級數展開對()做近似,此時Δ()可以寫為

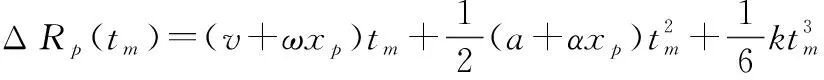
(7)

綜上,含有個散射點的機動目標回波具有如下形式:

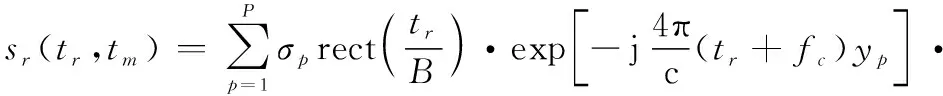
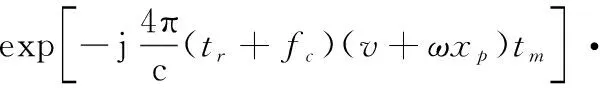
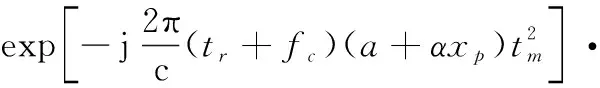
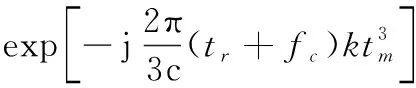
(8)

可見機動目標回波在慢時間域為多項式相位信號。

2 平動多項式參數估計

2.1 相位差分

盡管各散射點平動歷程的一致性為平動參數估計帶來了便利,但從式(8)可以明顯看出,平動和轉動對回波相位造成的影響在數學表達式上基本相同,這會使轉動參數影響到平動參數的估計值。同時,對式(8)進行脈沖壓縮后回波能量分布在多個距離單元也給平動參數估計帶來了困難。

為了準確估計平動參數,采用相位差分的方法對回波進行處理:

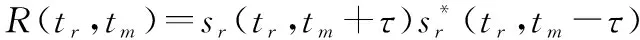
(9)

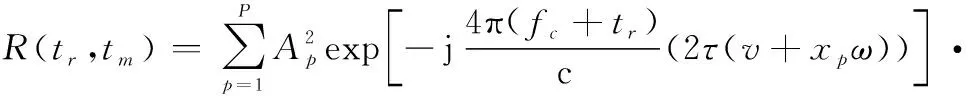
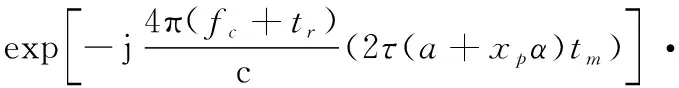
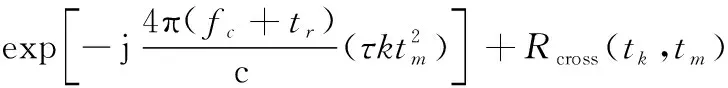
(10)

式中:=rect();(,)表示由相位差分造成的交叉項,設一個與散射點不同的散射點,則(,)可以表示為

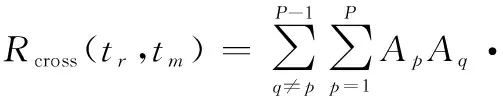
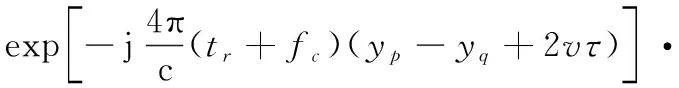
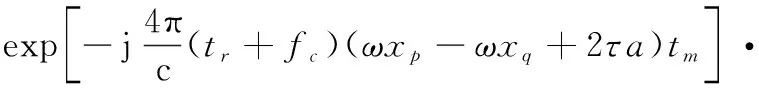
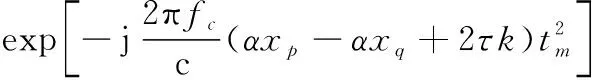
(11)

事實上,平動參數與轉動參數雖然會對回波造成相似的附加相位,但二者的尺度存在很大的差異。例如,空中目標的速度通常在音速附近,即340 m/s,若目標速度與雷達視線方向的夾角為88°,則目標的徑向速度約為11.8 m/s,而ISAR成像過程中,目標轉動的總角度約為3°～5°,設ISAR成像總時間2 s,則目標轉動速度約為0.035 rad/s,即便=10 m,的大小也僅有035,遠小于目標徑向速度。在進行相位差分處理時一般選取較小的時延常數,若=0.001 s,則式(10)中的僅有0.000 35,無論是對于包絡還是相位,該參數的影響都是能夠被忽略的,而平動參數遠大于轉動參數,因此其對回波相位的影響不能被忽略。綜上,式(10)能夠被近似為

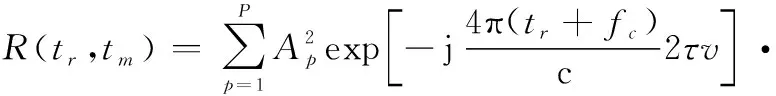
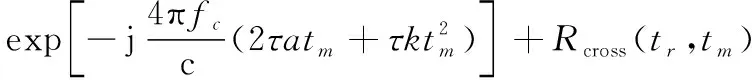
(12)

對回波進行脈沖壓縮,得到的結果為

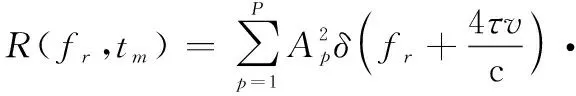
(13)

式中：為狄拉克函數。

2.2 基于LVD的平動參數估計

由式(13)可見,在進行相位差分處理后,回波的能量聚焦于=-4c對應的距離單元,取該距離單元的回波信號()用于平動參數估計,則()可以被表示為

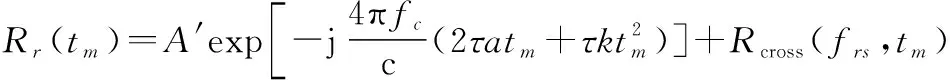
(14)

式中:

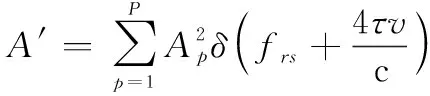
(15)

LVD具有良好的參數估計性能,且在信號存在多個分量時能夠有效抑制交叉項對參數估計的干擾。LVD的核函數為

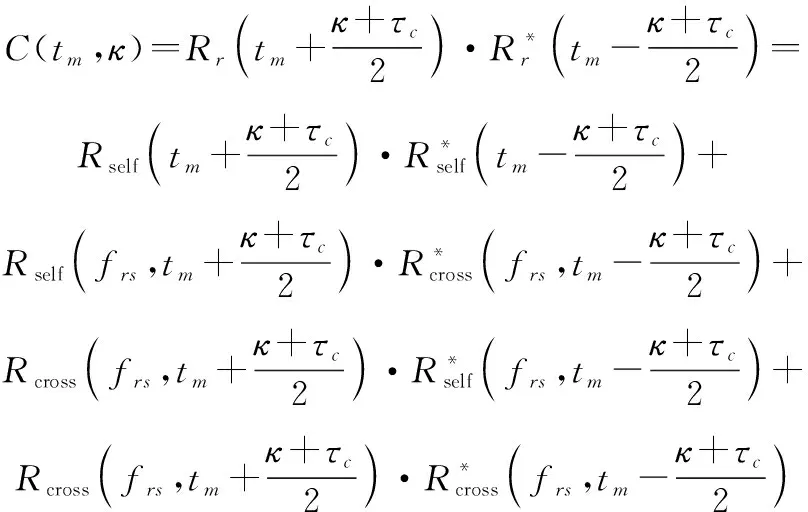
(16)

式中:表示時延變量;表示一常數;表示自項，即式(14)中除去(,)以外的部分。關于LVD交叉項抑制的原理,文獻[30]給出了詳細的分析,在此不再贅述。因此本節著重分析LVD變換中自項共軛相乘和(,)共軛相乘的結果。

用表示式(16)中自項共軛相乘的結果,其表達式為

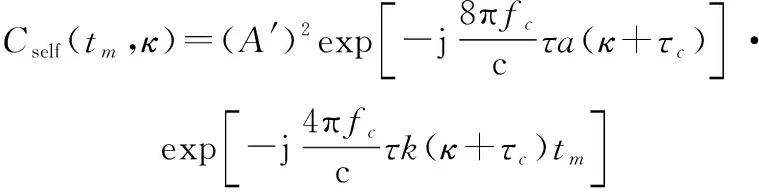
(17)

參考Keystone變換,設一個新的慢時間:

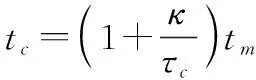
(18)

此時可寫為

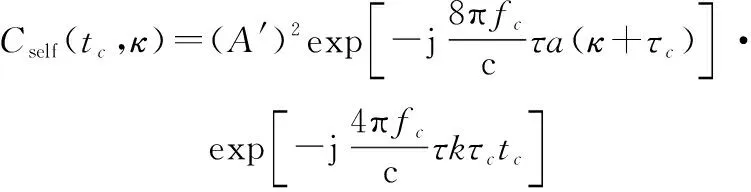
(19)

對式(19)在域和域同時進行傅里葉變換:

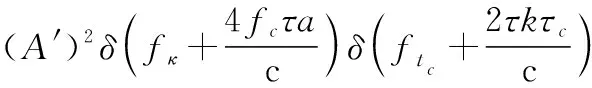
(20)

式中:FT 表示傅里葉變換;和分別為和經傅里葉變換后對應的頻率。可見在進行LVD變換后,存在唯一峰值,且峰值位置僅和與有關。

對于(,),由于狄拉克函數僅在自變量取0時存在響應,因此(,)實際上僅包含滿足=條件的交叉項,此時(,)可以被寫為

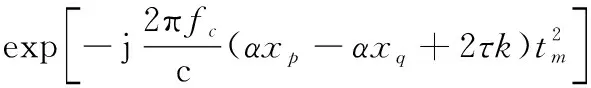
(21)

經過LVD變換后,式(21)變為

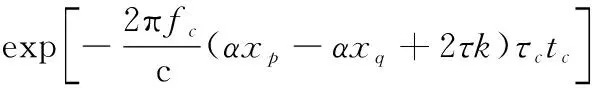
(22)

式中:

(23)

對于空間中兩個不同的散射點,當其滿足=時,必有-≠0,且當取不同的散射點和時,-也各不相同。式(22)經過傅里葉變換后,(,)的各個分量將分別形成尖峰且峰值位置各不相同。而在經過LVD變換后,所有分量的峰值都聚焦于同一位置,其幅度將遠遠大于(,)中任何分量。

根據以上原理,可以通過峰值搜索的方式得到平動參數的估計值:

{, }=argmax|LVD[()]|

(24)

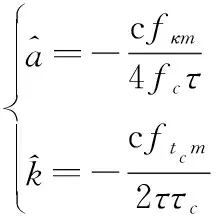
(25)

式中:表示峰值處對應的; 表示峰值處對應的;LVD[·]表示LVD變換。

利用平動參數估計值構造平動補償函數,并對回波進行補償:

(26)

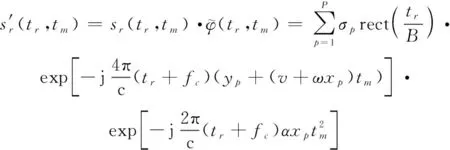
(27)

經過補償后,平動加速度和平動二階加速度對回波的影響已經被消除,僅剩平動速度對回波的影響依然存在。為了保證補償精度,利用最小圖像熵準則估計平動速度。首先構造平動速度估計函數:

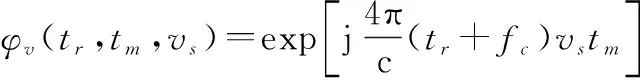
(28)

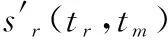
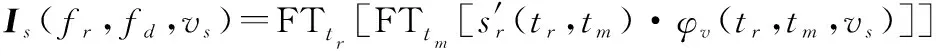
(29)

當=時,由平動速度造成的附加相位被完全補償,此時信號在圖像域的熵達到最小,根據此原理可以得到平動速度的估計值。圖像熵的定義為

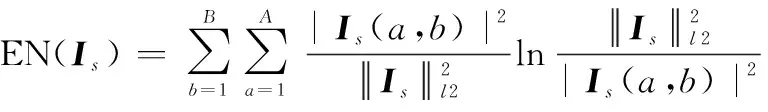
(30)

式中：表示圖像對應的矩陣;和分別為矩陣的行數和列數。根據式(29)和式(30),對進行估計:

{}=argmin|EN((,,))|

(31)

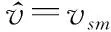
(32)

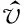
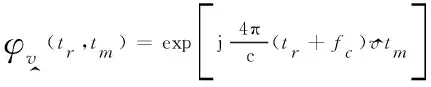
(33)

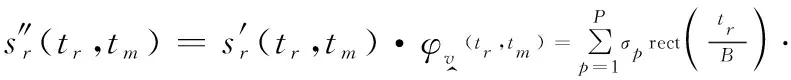
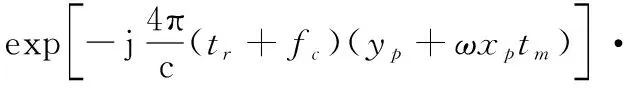
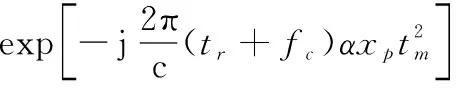
(34)

至此平動補償已全部完成。

3 基于LVD的機動目標平動補償流程

根據第2節的分析論證可以得出,基于LVD的機動目標平動補償算法流程如下。

對回波(,)進行相位差分。

選出均方根值最大的距離單元的回波()。

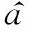
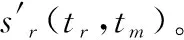
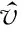
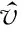
算法流程圖如圖2所示。

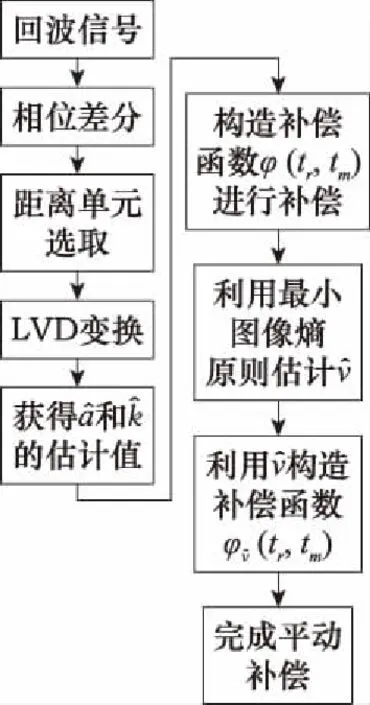
圖2 流程圖Fig.2 Flow chart

4 實測數據實驗

利用yake-42實測數據對算法進行驗證,該數據由中心頻率5.52 GHz,帶寬400 MHz,脈沖重復頻率100 Hz的雷達測得,數據共含有快時間采樣點數256點,慢時間采樣點數256點。該數據RD成像的結果如圖3所示。

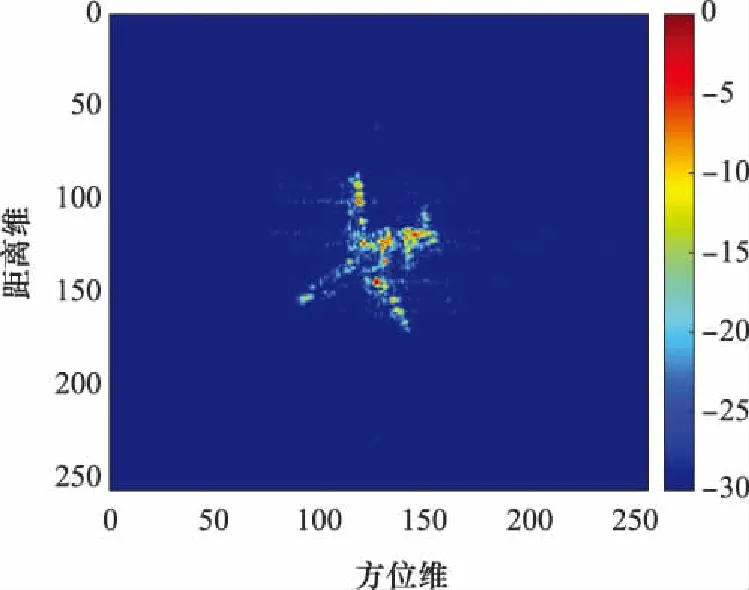
圖3 實測數據yake-42的RD成像結果Fig.3 RD imaging results of measured data yake-42

對yake-42加入平動影響,平動參數分別為:=11.5 m/s,=7 m/s,=4 m/s。目標一維距離像如圖4所示。

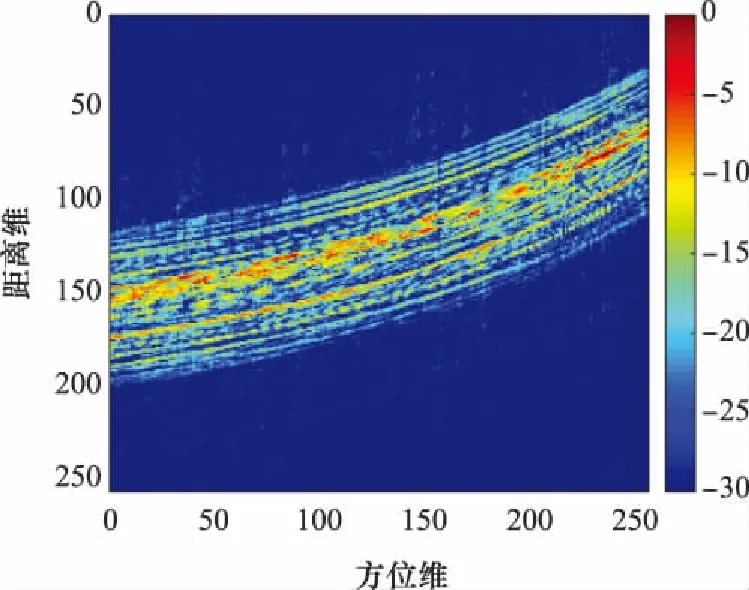
圖4 含平動影響的一維距離像Fig.4 One dimensional range profile with translational effects

可見在添加了平動影響后,目標的距離像出現了顯著的非線性彎曲。

對添加了平動的回波按照第3節給出的算法流程進行處理,并以圖像形式給出主要步驟對應的結果:對回波信號進行相位差分,得到的結果如圖5(a)所示;取能量最大的距離單元的回波進行LVD變換,得到的結果如圖5(b)所示;構建平動補償函數對平動加速度和平動二階加速度補償后得到的距離像如圖5(c)所示;利用最小圖像熵原則進一步補償平動誤差后的距離像如圖5(d)所示;平動補償后回波的RD成像結果如圖6所示。

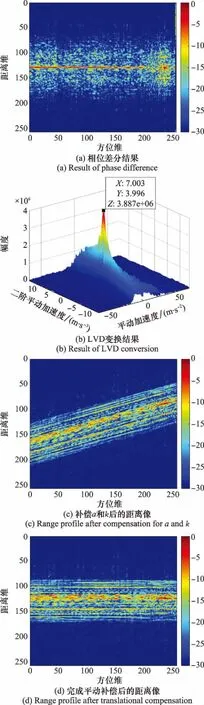
圖5 主要步驟結果Fig.5 Results of main steps

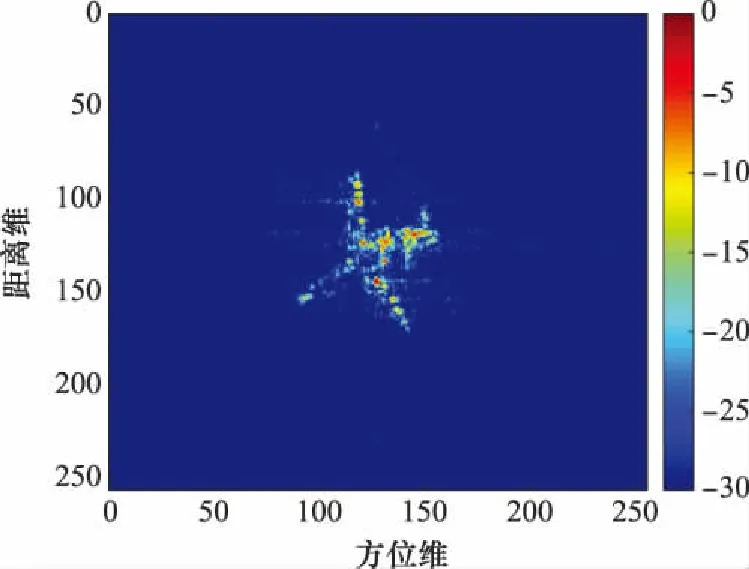
圖6 平動補償后RD成像結果Fig.6 RD imaging result after translational compensation

可見在經過相位差分處理后,回波能量都聚焦于同一距離單元,選擇該單元的回波進行LVD變換,得到平動加速度和二階平動加速度的估計值分別為7.003 m/s和3.996 m/s,與本實驗設定值基本一致。利用上述參數補償和對回波的影響后,回波距離像由非線性彎曲變為了線性彎曲,證明此時回波中僅剩下平動速度的影響未被補償。利用最小圖像熵原則對回波進一步補償后,回波距離像變得平直,對采用本文方法進行平動補償后的回波進行RD成像,其結果與圖3基本一致。一系列實驗證明本文方法能夠有效實現對機動目標的平動補償。

為了驗證本文方法的優越性,采用圖像質量評價指標-粒子群優化(image quality evaluation metric-particle swarm optimization, IQEM-PSO)算法和平均距離像相關+多特顯點法作為對照組。在信噪比為-5 dB的環境下,各方法平動補償后RD成像的結果如圖7所示。

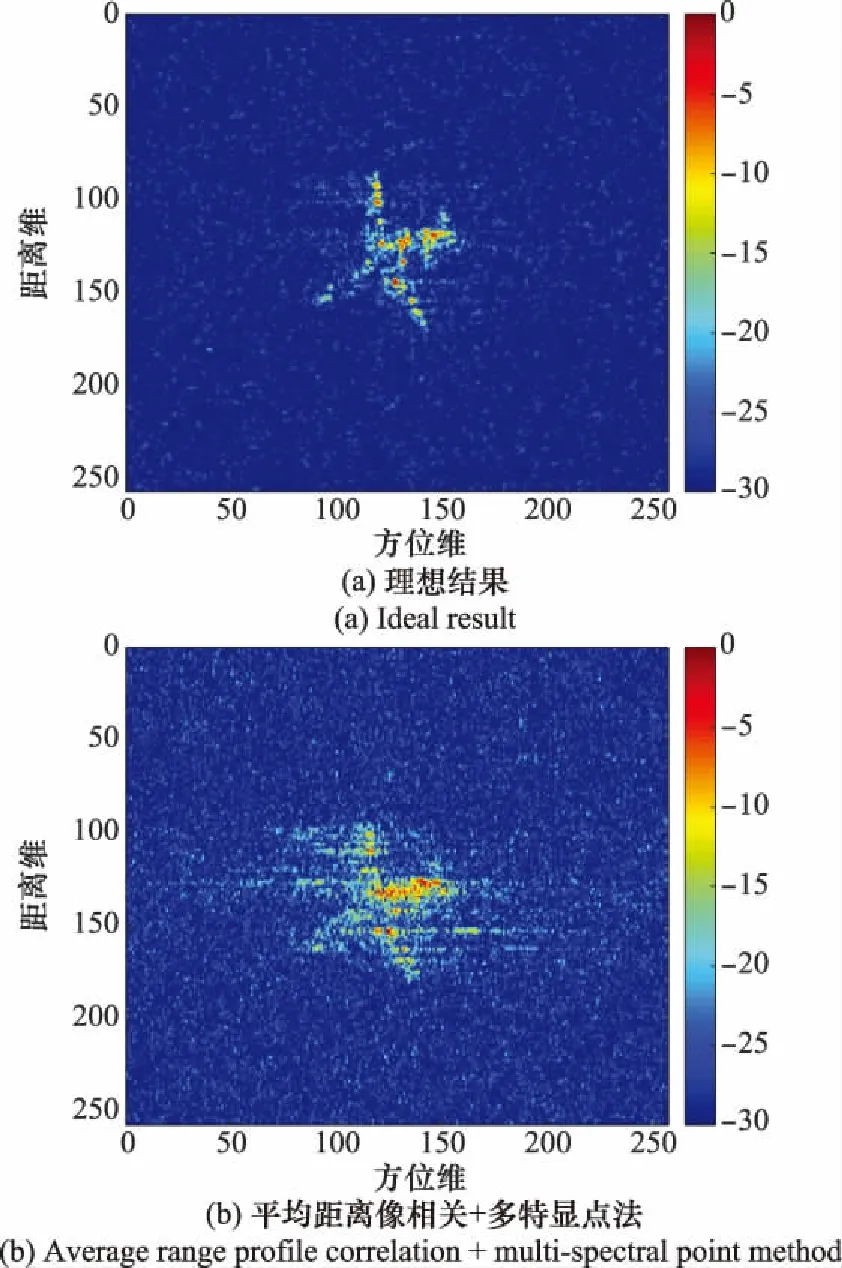
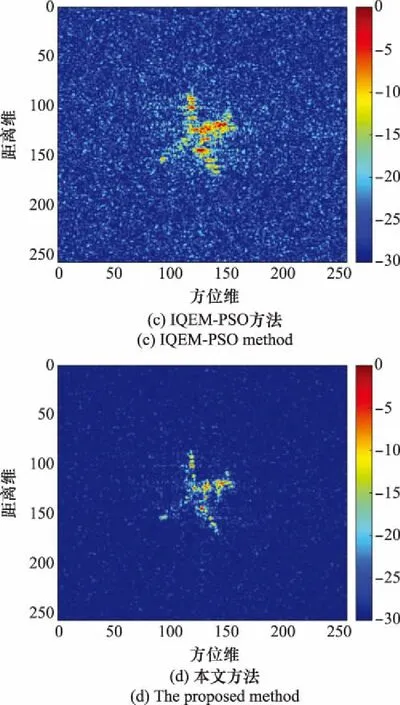
圖7 不同方法結果對比Fig.7 Comparison of results for different methods

可見平均距離像相關+多特顯點法的結果存在較為嚴重的散焦,說明對于低信噪比環境下的機動目標,采用平均距離像相關+多特顯點法進行平動補償難以獲得理想的結果。IQEM-PSO方法的結果一定程度上優于平均距離像相關+多特顯點法,但其依然存在散焦。這是由于IQEM-PSO在低信噪比環境下容易收斂于局部最優解。相比之下,采用本文方法進行平動補償的結果聚焦良好,與理想結果十分接近。這證明了本文方法在低信噪比環境下具有較好的穩定性,并在性能上較傳統方法更具優越性。

最后驗證本算法在低信噪比下的性能。當信噪比分別為-6 dB,-9 dB,-12 dB時,利用本文方法得到的平動補償結果如圖8所示。

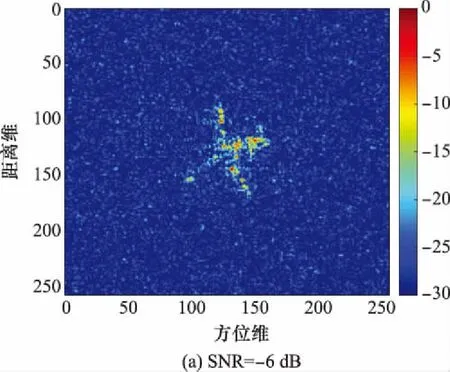
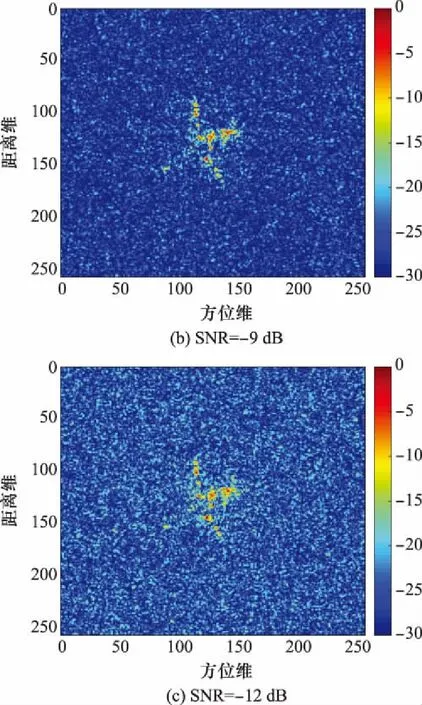
圖8 低信噪比性能驗證Fig.8 Performance verifications under low signal to noise ratio

可見在信噪比為-6 dB時,本文方法所得的結果除了噪聲點幅度略微增強外,與圖7(d)基本一致。當信噪比為-9 dB時,本文方法依然能有效補償目標平動,但相比于圖8(a),圖8(b)中目標的方位產生了一定程度的偏移。當信噪比為-12 dB時,幾乎難以分辨出目標和噪聲,但根據幅度較大的幾個散射中心來看,本文方法在-12 dB時依然能取得一定的效果。這足以說明本文方法在低信噪比環境下具有較好的魯棒性。

5 結 論

本文提出了一種基于LVD的ISAR成像參數化平動補償方法,以實現對機動目標穩定精確的平動補償。該方法首先對回波進行相位差分來完成能量聚焦,而后利用LVD估計平動加速度和二階平動加速度,并構造函數補償二者對回波的影響,最后采用最小圖像熵準則估計和補償平動速度。實測數據實驗證明了本方法的有效性,以及在低信噪比下的穩定性與優越性。