改進螢火蟲算法及其收斂性分析

張大力, 夏紅偉, 張朝興, 馬廣程, 王常虹,*

(1. 哈爾濱工業大學航天學院, 黑龍江 哈爾濱 150001; 2. 上海航天控制技術研究所, 上海 201109)

0 引 言

社會性生物的某些集體行為往往呈現出尋優的本質,通過對這類行為的公式化,得到了一類被稱為群智能算法的優化算法,蟻群優化(ant colony optimization, ACO)算法、粒子群優化(particle swarm optimization, PSO)算法、人工蜂群(artificial bee colony, ABC)算法等均屬此列。由于算法簡單靈活、魯棒性好,可用于求解許多傳統方法無法解決的NP-hard問題,如旅行商問題、裝箱問題等,已經廣泛應用于人工智能、通信網絡和工業生產等領域。

螢火蟲算法(firefly algorithm, FA)是英國學者Yang于2008年提出的一種元啟發式算法。該算法通過模擬自然界中螢火蟲個體之間相互吸引的理想化行為達到尋優目的,一經提出便受到國內外研究人員的關注,廣泛應用于計算機科學、復雜方程求解、結構和工程優化領域。但許多構造的和現實的優化問題具有大量的局部最優解,容易使算法因種群多樣性的快速衰減而陷入早熟停滯,大幅降低優化效果。同時,大量局部最優對種群的吸引可能導致算法不斷震蕩而無法收斂。有學者通過引入自適應或隨機機制針對上述問題進行改進。Gandomi等采用12種不同的混沌映射對參數進行自適應調節,其中高斯映射調節吸引度參數的改進算法取得了一定效果,但性能提升有限,尋優成功率不高。Yu等設計了一種自適應步長策略來提高算法的全局探索能力,每個個體的隨機步長根據當前和歷史信息分別計算,然而實際尋優效果與標準算法區別很小。Altay等將該改進算法用于調節數字水印技術中的比例因子,由于缺乏與標準算法的橫向對比,不足以說明改進算法的優越性。Verma等在算法初始化階段引入反向學習策略提高算法收斂速度,在迭代過程中采用基于維度的位置更新方法跳出局部最優,但與其他優化算法相比沒有體現出明顯的競爭力。Manju等參考量子PSO提出了量子FA,并利用基于二次插值的重組算子改進搜索過程,提高了算法的收斂速度和尋優能力,但無法處理復雜病態優化問題。柳長源等引入了一種驅散機制,若種群最優值在連續多次迭代后未發生變化,則對最優個體采用柯西分布進行變異,聚集在最優個體附近的個體采用均勻分布進行驅散,從函數優化結果來看改進效果并不顯著。劉景森等提出了一種具有振蕩、約束和自然選擇機制的改進策略,提高了算法對高維問題的求解能力,但是增加了額外的調節參數,不利于推廣應用,其收斂性證明仿照PSO算法證明的思路,簡化到二維空間進行分析,無法向高維情況推廣。部分學者選擇從個體信息交互的角度對算法進行改進。Wang等提出了一種隨機吸引模型,通過將個體與其鄰域內有限個其他個體進行通信,降低了算法計算復雜度,但尋優性能沒有明顯提升。在此基礎上,Dhal等進一步考慮粗糙集和局部搜索機制,提出了一種隨機吸引粗糙FA,并成功應用于圖像分割過程,但與標準算法及其他傳統優化算法相比沒有明顯的競爭力。Shan等通過分布式并行技術將種群劃分為多個子群,子群之間基于4種不同的通信策略進行信息交換,但每個子群的尋優能力偏弱,不能保證整體的尋優效果,且增加了額外的配置參數,適用性不強。Elakkiya等提出了一種基于社區啟發的改進策略,個體只被由個較優個體組成的所謂社區中的個體吸引,并給出了社區規模的自適應更新機制,降低了計算復雜度,但無法保證尋優精度。還有一種改進策略是在FA中引入其他算法的思想。Zhao等借鑒ABC算法的思想將螢火蟲種群分為領導者、開發者和跟隨者3種角色,并為每個角色分配了一種學習策略,用來平衡算法的探索和挖掘能力,但沒有取得顯著的性能改進。Xing等為了使算法跳出局部最優,引入了遺傳算法中的變異算子,同時仿照PSO算法將全局最優納入到位置更新公式中,改進算法用于解決協同干擾資源分配問題,尋優結果與標準算法相比有少許提升。薛晗等結合文化算法和FA的優點,將迭代過程中獲取的經驗和知識組成信仰空間,并設計了一套規則來影響種群更新,但算法沒有足夠的跳出局部最優的能力。Gupta等將引力搜索和FA通過串行運行的方式結合起來,提出了一種混合引力搜索FA,計算復雜度較高,尋優能力沒有明顯提升。此外,Cheng等和Xue等采用混合編碼的形式對個體進行編碼,利用組合變異、協同進化等方式加快算法收斂速度,但該方法只適用于解決離散工程優化問題,缺乏適用性。

基于以上分析可以看出,目前FA仍然具有較大的改進潛力,并且理論分析比較薄弱,也在一定程度上制約了FA的進一步改進和發展。因此,本文提出一種改進FA(improved FA, IFA),以提升算法性能。首先,介紹FA的基本原理。其次,給出新的個體位置更新機制。圍繞種群更新過程,引入位置置換變異策略和差分進化(differential evolution,DE)算法中的最優變異策略(DE/best/1),并給出算法流程。然后,給出改進算法收斂性的理論證明。最后,采用一組典型基準函數和裝箱問題對改進算法有效性進行驗證。

1 FA基本原理

FA受螢火蟲群體的集聚性啟發,其仿生原理如下:搜索空間中的單個元素代表螢火蟲個體;擬優化的目標抽象為個體所在位置的亮度,衡量個體位置的優劣并決定其移動方向;元素搜索和更新的尋優過程模擬個體間的吸引和移動行為。

算法數學描述如下:

(1) 個體的位置記為=(1,2,…,),其亮度即為該位置對應的目標函數值()。

(2) 個體與間的吸引度更新公式定義為

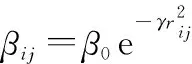
(1)

式中:為初始吸引度,一般取值為1;為光強吸收系數,一般取值為1;為個體間的笛卡爾距離,有

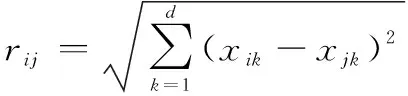
(2)

(3) 個體被吸引并向其移動的位置更新公式為

(3)

式中:為算法迭代次數;為步長因子;為隨機數,服從均勻分布或高斯分布。

2 IFA

威廉·奧卡姆曾言,“如無必要,勿增實體”,這就是著名的“奧卡姆剃刀定律”。從優化算法設計的角度來詮釋,可理解為在效果相同或相近的前提下,盡量選擇簡單框架和規則。在這種思想的指導下,本文提出以下改進策略。

2.1 隨機擾動策略

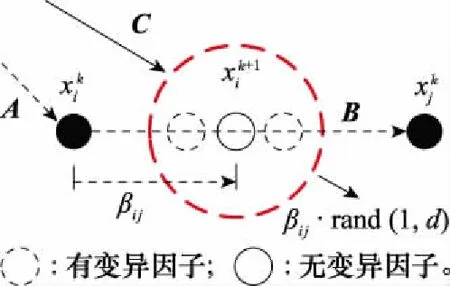
圖1 吸引力項運動特征Fig.1 Motion characteristic of attraction term

由于式(3)第3項隨機項的變化是獨立的,沒有利用個體和種群信息,因此其變化很難與個體的進化相匹配。一方面,如果取值過小,那么較小的搜索半徑無法提供跳出局部最優的能力,如果取值較大,則會因為較大的搜索半徑導致較慢的收斂速度和較低的收斂精度。另一方面,一旦在隨機項中引入個體信息,那么可與改進后的第2項合并同類項,在功能上被其覆蓋。

基于以上考慮,向原位置更新式(3)中引入一個隨機擾動因子,使得吸引力項擁有一個隨機權重,并去掉式(3)第3項,有

(4)

為保證式(4)在初始階段的搜索能力,將吸引度更新為

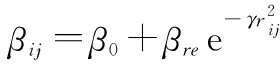
(5)

式中:為吸引度調節尺度,根據調試經驗建議取值范圍為07～09。

隨機擾動因子的引入提高了個體的搜索范圍。一方面,在算法初始階段,個體間距離較大,式(5)表示的隨機權重簡化為·,此時搜索步長較長,算法能夠在全局范圍內進行尋優,一定程度上提高了算法的全局探索能力;另一方面,在算法迭代后期,個體間距離大幅減小,隨機權重簡化為(+)·,而此時搜索步長較小,算法能夠在當前位置的鄰域深度挖掘。個體搜索范圍的提升使得種群在運動過程中能夠覆蓋到更多搜索空間中的區域,如圖2所示。

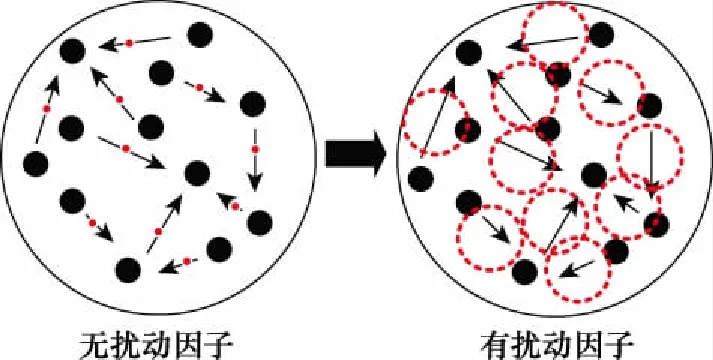
圖2 種群運動趨勢和個體分布情況Fig.2 Population movement trend and individual distribution

下面對隨機擾動因子的選擇進行分析。典型的隨機分布有均勻分布、正態分布、柯西分布、列維分布等。為了更直觀地區分不同分布的特征,給出上述分布100 000個樣本的分布直方圖,如圖3所示。

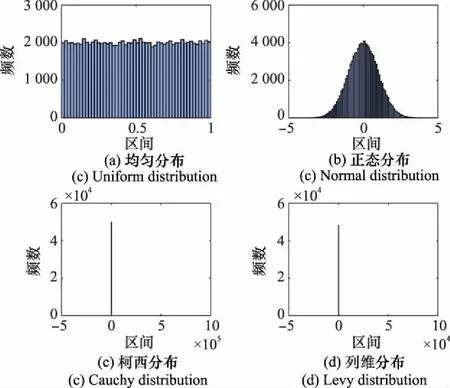
圖3 4種不同概率分布的100 000樣本分布Fig.3 Four different probability distributions of 100 000 random samples

由圖3可以看出,均勻分布產生的樣本分布均勻且取值區間較小,選擇均勻分布作為隨機擾動因子可獲得在各個方向上更加穩定的搜索能力。正態分布產生的樣本呈現出左右對稱、中間高兩側低的鐘型分布特征,在原點附近取值的概率較高,離原點越遠取值概率越低,選擇正態分布作為隨機擾動因子,存在初始階段收斂慢的情況,不能保證算法收斂速度。柯西分布和列維分布產生的樣本呈現出明顯的厚尾特征,在原點附近取值的概率較高,偶爾會出現非常大的樣本,選擇柯西或列維分布作為隨機擾動因子,算法搜索能力不穩定,且產生的大樣本很有可能使個體更新超出搜索空間,精度和收斂速度均無法保證。基于以上分析,隨機擾動因子首選均勻分布,在第4.1節中給出仿真，對以上分析做進一步說明。

2.2 雙重變異策略

為進一步提升算法尋優性能,本文圍繞個體和種群的更新過程增加兩個變異機制。

221 位置置換變異策略

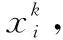
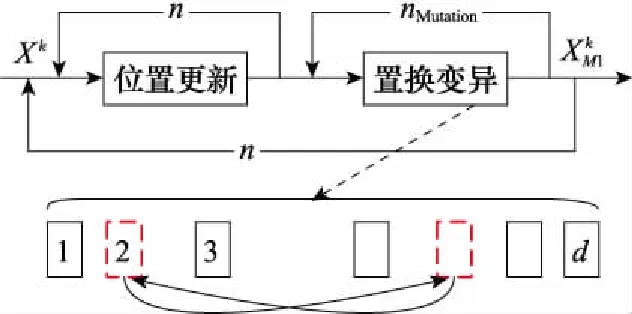
圖4 位置置換變異原理和種群更新流程Fig.4 Principle of position substitution mutation and population renewal process

參數的取值是位置置換變異策略的關鍵。一方面,由于該操作在個體位置更新后進行,且嵌套于種群更新過程中,因此不能過大,否則會提高算法計算復雜度,降低收斂速度。另一方面,若次數太少,個體位置變化較小,無法達到跳出局部最優的目的,降低尋優精度。因此,置換變異至少2次,至多建議不超過5次,本文取=3。

222 DE/best/1變異策略

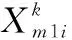
(6)

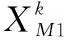
圖5 DE/best/1/變異種群更新流程
Fig.5 DE/best/1 cross mutation population renewal process

DE/best/1變異操作的執行次數為。由于該部分沒有循環嵌套,可以取大一些的數,從而充分利用歷史最優信息指導搜索過程,提高算法收斂精度。參考差分進化算法的取值,可取種群規模。

兩種變異策略得到的子代種群采取與父代種群競爭的模式選取進入下一輪循環的種群,在每輪迭代中保留較優個體,提升整體種群質量。

2.3 算法平衡性分析

全局探索與局部挖掘能力是群智能優化算法解決問題的核心,二者之間的平衡對算法性能至關重要。研究普遍認為,在算法開始階段應以全局探索為主,在后期應以局部挖掘為主。改進算法能夠很好地滿足此規律。在算法迭代初始階段,個體間相距較遠,從位置更新式(4)和DE/best/1變異策略式(6)可直觀地看出,此時算法有較大的搜索步長,能夠在解空間內進行全局探索。算法迭代后期,種群不斷聚集,搜索步長隨之減小,此時算法的局部挖掘能力得到不斷強化。第221節所述的位置置換變異策略是對個體自身信息的突變,該操作不受迭代過程的影響,無論在迭代前期還是迭代后期均能使個體有效地跳出當前位置,從而避免算法陷入局部最優。需要注意的是,在實際運行中,全局探索和局部挖掘能力是算法各個策略共同觸發的,沒有明確的界限。

2.4 算法流程

下面給出改進算法的流程。

初始化控制參數，，，位置變異次數為，DE/best/1變異執行次，種群規模為，搜索空間下界為，上界為，最大迭代次數為MaxGeneration。

構建服從均勻分布的初始種群，計算適應度和當前全局最優解g。

取種群中的一個個體，判斷其與其他個體的吸引關系，根據式(2)、式(4)、式(5)更新該個體的位置并進行限位，同時更新全局最優值g，該步驟執行次。

根據第221節給出的策略對步驟3中選定的個體進行位置置換變異，該步驟執行次。

步驟3～步驟4連續執行，重復次數為次，得到子種群1。

根據第222節給出的策略對種群1進行變異操作，同時更新全局最優值g。該步驟執行次，得到子種群2。

父代種群和子代種群拼接并排序后截斷保留 維數據，得到下一輪迭代的父代種群。

本文設置停止準則為迭代次數達到MaxGeneration，若滿足條件，則終止判斷，輸出優化結果并可視化；若不滿足條件，則重復步驟3～步驟7。

2.5 算法計算復雜度分析

結合算法流程進行分析,為了簡便這里記為迭代次數,為適應度函數的計算量,那么算法語句總的執行次數可以表示為·[(5+)·+·(+4)·+(+7)·],此時改進算法的時間復雜度為(··)。顯然,算法的計算復雜度與問題本身的復雜度直接相關,主要由適應度函數計算量和算法計算量決定。

3 收斂性證明

3.1 隨機算法的收斂準則

Wets給出了一般隨機優化算法收斂性判別準則,下面重述其主要結論。

假設有隨機優化問題[,],其迭代方式為,第次迭代結果,則+1=(,)。其中,為適應度函數,為解空間,是次迭代產生的所有解。

在Lebesgue測度空間定義搜索的下確界:

=inf(∶[∈|()<]>0)

(7)

式中:[]表示集合上的Lebesgue測度。根據式(7)定義最優解區域為

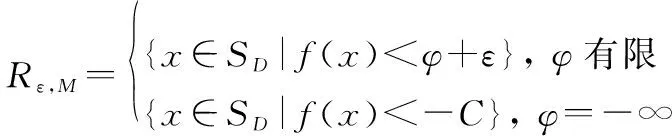
(8)

式中:>0且足夠小,>0且足夠大。若算法找到了,中的一個點,則算法收斂。

下面給出算法收斂的充分條件:

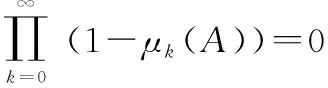
全局搜索收斂

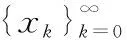
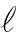
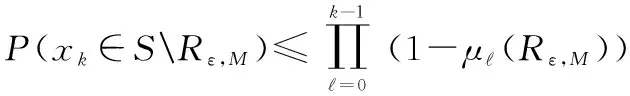
(9)

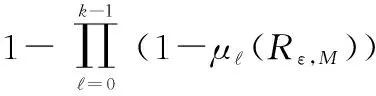
(10)

(11)

證畢

3.2 改進算法基本概念的數學描述

螢火蟲位置狀態和位置狀態空間

螢火蟲位置的狀態=(,),由螢火蟲的位置和全局最優值構成,所有可能的個體位置狀態的集合稱為螢火蟲的位置狀態空間,記為={=(,)|,∈,()<()}。其中,螢火蟲個體在一次迭代過程中產生的兩組子種群的個體位置記為1和2,其位置狀態分別記為1=(1,)和2=(2,),為包含兩子種群個體的位置狀態空間。

群體狀態和群體狀態空間

種群位置狀態集合稱為群體狀態,記為={,,…,},所有群體狀態構成的群體狀態空間記為={=(,,…,),∈,1≤≤},其中子群位置狀態記為1=(11,12,…,1)和2=(21,22,…,2),且包含兩子群狀態空間。

3.3 IFA的馬爾可夫模型建立

對?=(,gb)∈,?1=(1,gb)∈位置狀態由轉移到1記為1()=1。

螢火蟲的位置狀態由轉移到1的轉移概率為

(1 ()=1)=(→1′)·(gb→gb′)·(1′→1)·(gb′→gb″)

(12)

式中:(→1′)為式(4)對應的轉移概率;(gb→gb′)為該步驟全局最優位置的轉移概率;(1′→1)為步驟4對應的轉移概率;(gb′→gb″)為該步驟更新全局最優的轉移概率。

螢火蟲位置狀態由轉移到1,意味著→1′,gb→gb′,1′→1,gb′→gb同時成立。作為子種群,有

(→1′)=1

(13)

全局最優位置gb的轉移概率為

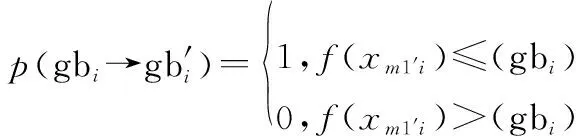
(14)

位置狀態由1′→1的概率為

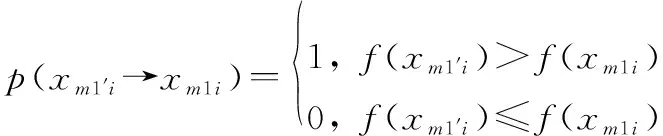
(15)

全局最優位置的再次轉移概率為

(16)

證畢

對?=(1,2,…,)∈,?1=(11,12,…,1)∈,群體狀態由轉移到1,記作1()=1。

螢火蟲位置群體狀態由轉移到1的轉移概率為

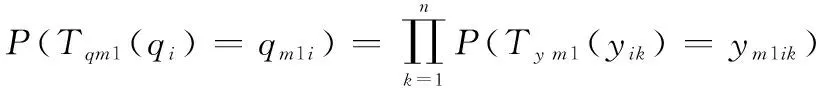
(17)

若螢火蟲位置群體狀態由轉移到1,那么表示中所有個體的位置狀態同時轉移到1中所有個體的位置狀態,即1(1)=11,1(2)=12,…,1()=1同時成立。

證畢

在IFA算法迭代中,對?1=(11,12,…,1)∈,?2=(21,22,…,2)∈,記作2(1)=2。

螢火蟲位置群體狀態由1轉移到2的轉移概率為

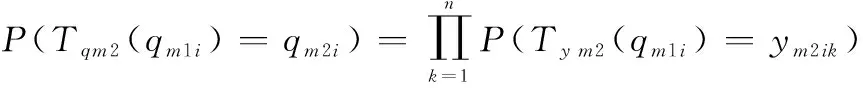
(18)

若螢火蟲位置群體狀態由1轉移到2,那么有1中所有個體位置狀態同時轉移到2中所有個體位置狀態,即2(1)=21,2(1)=22,…,2(1)=2同時成立。在迭代過程中,第二次變異操作個體的狀態轉移與種群狀態轉移有關,根據式(7)有

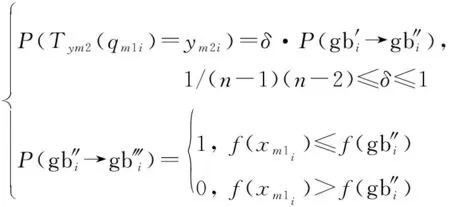
(19)

證畢

對?=(1,2,…,)∈,=(1,2,…,)∈,將螢火蟲位置的群體狀態轉移到記作()=。

螢火蟲位置群體狀態由轉移到的轉移概率為

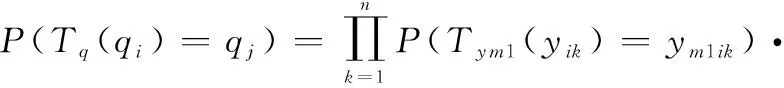
(20)

式中:為對父代種群和兩子種群進行排序和截斷操作,(gb?→gb)為尋找種群中的最優個體的轉移概率。

若螢火蟲位置的群體狀態由一步轉移到,就意味著位置的群體狀態發生了集體轉移,由定理1～定理3可推出最終的轉移概率公式。

證畢

螢火蟲的位置群體狀態序列{();≥0}是離散時空上的有限齊次馬爾可夫鏈。

首先,對于任何一個優化算法來講,其搜索空間都是有限的,任意個體狀態=(,g)中的,g也是有限的,所以位置的狀態空間是有限空間。又由于=(,,…,)由個個體組成,為大小有限的正整數,故螢火蟲位置的群體狀態也是有限的。

其次,?(-1)∈,?()∈,其狀態轉移概率(((-1))=())是由群體中所有個體的轉移概率和兩子群的轉移概率決定。由定理1～定理3,可得

(1((-1))=1(-1))=((-1)→1′(-1))·(g(-1)→g′(-1))·(1′(-1)→1(-1))·(g′(-1)→g(-1))

(21)

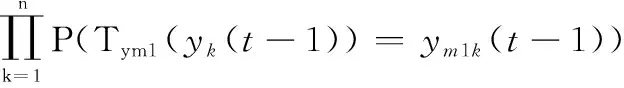
(22)

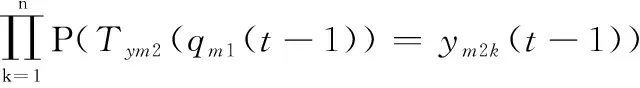
(23)

則

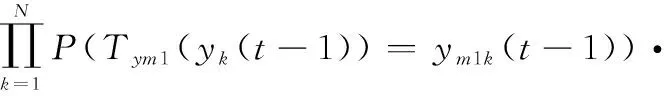
(24)

通過以上分析,(((-1))=())僅與-1時刻的位置狀態有關,故螢火蟲位置的群體狀態{();≥0}具有馬爾可夫性,且算法迭代與時間無關,所以該過程是齊次的。

證畢

3.4 IFA的收斂性分析

定義最小化問題∶→,?

min() s.t.∈

式中:={,,…,}為維決策變量,所有滿足約束的值構成的集合稱為可行域。位置最優位置狀態集為,其群體狀態集為={=(,,…,)|?∈,1≤≤}。

對閉集,?∈,有∑∈=1,意味著從狀態空間內的任何一點出發,始終無法達到以外的任意狀態。

對于個體位置狀態集{();>0},集合是空間上的一個閉集;對位置群體狀態集{();≥0},集合是空間上的一個閉集。

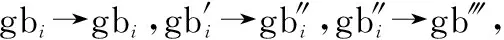
同理,假如?∈,??,→成立,那么至少存在一個個體的位置由的內部轉移至外部,又已證明是上的一個閉集,根據式(20),有(()=)=0,由閉集定義知,集合是空間上的一個閉集。

證畢

在螢火蟲位置群體狀態空間中,無法找到外的非空閉集,使其滿足∩=。

假設在位置群體空間中能夠找到一個閉集,滿足∩=,那么?∈,?∈,有(gb)>(gb)。根據式(20),其滿足各個組件不為0的條件,那么存在轉移概率(()=)≠0,即不是閉集。定理得證。

證畢

假設〈〉是一組服從rand(0,1)的隨機變量,且滿足獨立同分布,那么

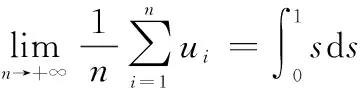
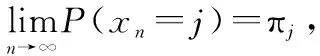
隨著螢火蟲位置群體狀態不斷迭代更新,當次數趨于無窮時,螢火蟲位置群體狀態序列必然進入最優集。

由定理6和定理7以及引理1和引理2得證。

在迭代次數趨于無窮時,IFA能夠以概率1收斂于全局最優。

一方面,在每次迭代過程中,IFA都保留了全局最優,從而保證了適應度的非增性,滿足收斂條件一;另一方面,根據定理9,當迭代次數趨于無窮時,螢火蟲位置的群體序列必然進入最優集,即找不到全局最優的概率為0,滿足收斂條件二。故IFA以概率1收斂于全局最優。

證畢

4 仿真實驗

由于實際應用中算法運行時間有限,故需通過固定時間的仿真實驗對算法有效性進行驗證。算法運行環境為Intel Core i5-3470處理器,CPU3.20 GHz,3.48 GB內存,Windows10,64位操作系統。

4.1 隨機擾動因子性能對比

為驗證第2.1節中的結論,對4種隨機擾動因子下的改進算法RIFA, GIFA, CIFA, LIFA進行仿真試驗和性能對比,R(平均)、G(正態)、C(Cauchy)、L(Levy)分別對應改進算法采用的隨機分布。選用4個典型基準函數,如表1所示。

算法參數設置情況為=1,=08,=1,=3,=40,取種群規模,=30,～U(04,09,1,),最大迭代次數為2 000。初始種群由問題域內進行隨機初始化產生。為提高結果的可信度,保證對比實驗客觀公正,對每一個測試,所有算法均獨立執行50次,取平均最優值、時間和成功率(success rate, SR)的統計結果進行比較,最優結果由粗體標出,仿真結果如表2所示。

表1 基準函數Table1 Benchmarks functions

表2 4種隨機擾動因子仿真結果Table 2 Four random disturbance factors simulation results

表2的統計結果顯示,隨機擾動因子選擇均勻分布時,在尋優精度、收斂時間和SR上的表現最好,對所有基準函數均能找到最優解;選擇正態分布時,算法收斂時間大幅提高,尋優精度和SR也出現了下降,特別是函數～的表現很差;柯西擾動因子的表現與正態分布類似,收斂時間比前者稍短,但尋優精度更加無法保證;列維擾動因子表現最差,運行效率最低,優化結果幾乎不可用。因此,改進算法的隨機擾動因子優先選擇均勻分布。

4.2 與其他算法的性能對比

選取已在實踐中檢驗過的優秀算法PSO、DE以及FA進行對比試驗。各個算法的參數設置情況如下:

(1) PSO:慣性權重=1,阻尼比=0.99,加速因子=15,=2.0。

(2) DE(DE/rand/1):縮放因子F為范圍在0.2～0.8的均勻隨機數,變異概率=0.2。

(3) FA:=02,=0.98,=2,=1。

(4) IFA參數同第4.1節。

其他仿真條件同第4.1節,仿真結果見表3。

表3 固定迭代次數仿真結果Table 3 Simulation results of fixed iterations

表3的統計結果顯示,對于函數～,改進算法均能夠找到最優解、精度和SR均好于對比方法,在和尤為明顯。但在平均仿真時間上,改進算法比其他算法長。這是由于PSO、DE和FA過早陷入局部最優,根據優化算法本身運行機制,如果沒有足夠的跳出局部最優的能力,那么會不斷加速收斂,因此其運行時間短于改進算法。

函數是典型的復雜病態二次函數,其全局最優位于狹窄的、拋物形的山谷中,缺乏有價值的信息,優化難度較大,比較考驗算法全局探索和局部挖掘能力。各方法對該函數進行優化的尋優曲線如圖6所示。

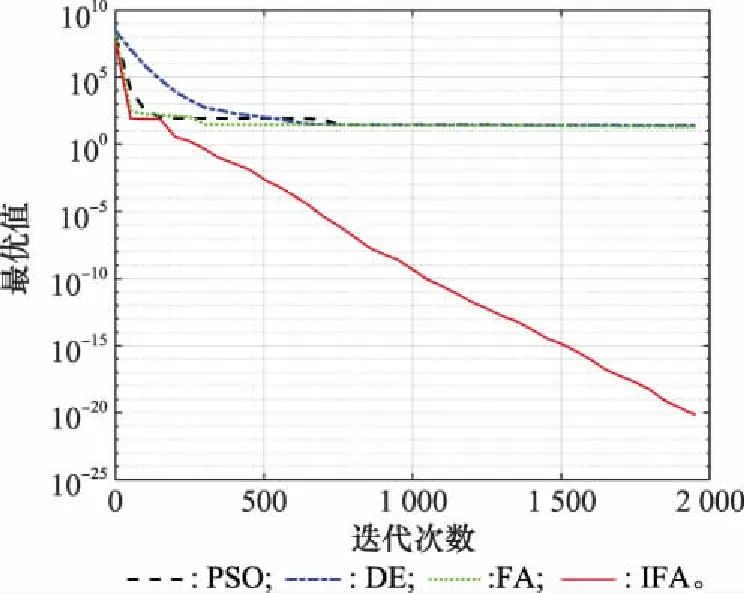
圖6 不同算法性能比較Fig.6 Performance comparison of different algorithms

由圖6可以看出,PSO、DE和FA均出現了早熟收斂現象,而IFA在短暫收斂后,在迭代到151步時成功跳出局部最優并最終達到極高的優化精度。現給出算法迭代150步到151步時的個體分布情況。由于個體維數較高,因此通過評估每個個體與平均個體在搜索空間中的相對距離得到個體分布散點圖,如圖7所示。

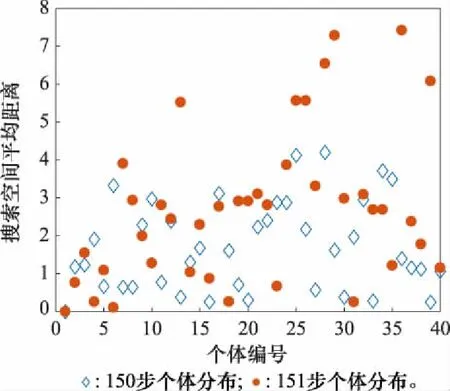
圖7 典型迭代時刻個體分布Fig.7 Individual distribution of typical iteration time

可以看出,種群在151步時部分個體突變至距離平均個體較遠的位置,獲得了更優解的同時,帶動種群整體移動,整體的多樣性比150步時有了明顯的提升。通過以上仿真和分析,證明了所提改進策略在基準函數優化方面的有效性。

4.3 裝箱問題實例

本文將IFA用于求解裝箱問題。裝箱問題是一個經典NP-hard組合優化問題,在運籌學、離散數學、計算機科學以及工業生產等方面有著廣泛的應用。

設有足夠數量的結構相同容量一致的箱子,,…,每個箱子的最大容量為。現有一組個物品,,…,，體積分別為(0<<,=1,2,…,)，需裝入箱內,要求在滿足約束的情況下打包所有物品,要求所需箱子數量盡可能的少。兩個約束分別為:① 所有物體均不可分割,需保持完整并恰好放入一個箱子中;② 每個箱子所放物品體積總和均不能超過容量上限。假設物品形狀對裝箱沒有影響,則該問題可描述為

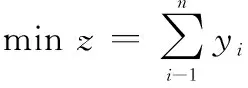
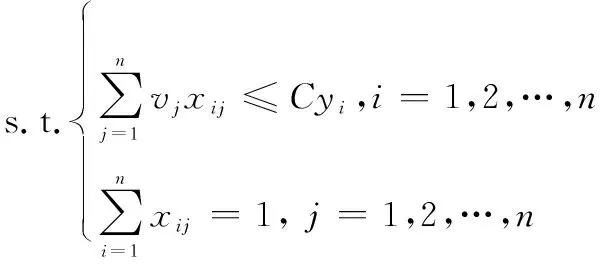
(25)

其中,

假設30個物品體積分別為[6,3,4,6,8,7,4,7,7,5,5,6,7,7,6,4,8,7,8,8,2,3,4,5,6,5,5,7,7,12],箱子容量=30。固定迭代1 000步,種群規模為20,其余參數不變。優化結果與PSO、DE和FA比較,算法收斂情況如圖8所示。

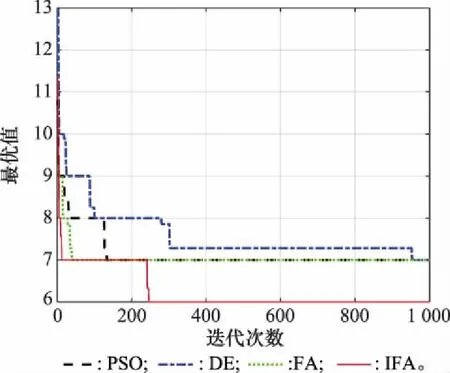
圖8 裝箱問題的性能比較Fig.8 Comparison on bin packing problem

由圖8可以看出,IFA僅需12步即可達到其他3種算法的優化效果,并且經進一步迭代后能夠跳出局部最優,從而得到更優的結果。表4給出了幾種優化算法的總體運行時間(total time,TT)、收斂時間(convergence time,CT)和最優結果(Best)。比較可知,IFA在優化結果和收斂速度方面都有著明顯的優勢。

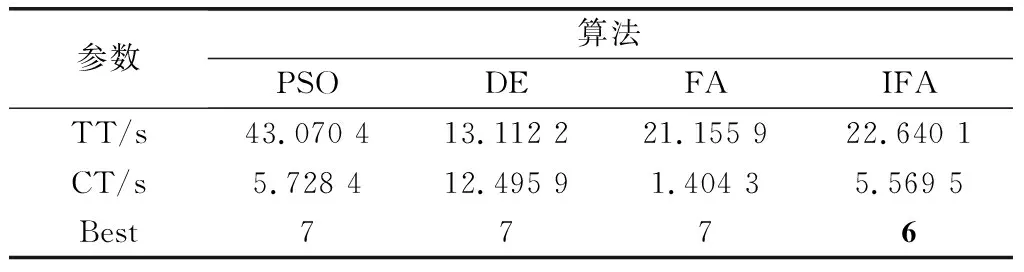
表4 裝箱問題優化結果Table 4 Optimization results of bin packing problem

5 結 論

本文為克服FA易陷入局部最優的缺陷,提出了IFA。首先分析了個體位置更新機制的特點,提出了一種隨機擾動策略,闡述了改進策略的有效性,并分析了不同擾動因子選取的可行性。通過引入元素置換變異策略和最優差分變異策略,提高了算法跳出局部最優的能力。基于隨機算法收斂準則和馬爾可夫過程的理論分析指出,改進算法在足夠大的迭代次數下能夠以概率1收斂到全局最優。對4種基準函數的仿真結果表明,隨機擾動因子選擇均勻分布時有最佳表現。在相同條件下與幾種經典算法相比,改進算法的收斂精度和SR更高,驗證了改進算法的優越性。將該方法對經典裝箱問題進行求解,得到了較好的優化結果,驗證了改進方法的有效性和實用價值。