考慮齒隙的多約束導引控制一體化設計方法

姜 尚, 魏 波, 梁偉閣, 孫東彥, 李進軍, 馬 野

(1. 海軍大連艦艇學院導彈與艦炮系, 遼寧 大連 116018; 2. 海軍工程大學兵器工程學院, 湖北 武漢 430033)

0 引 言

近年來,世界軍事強國不斷加快海軍戰略的轉型改革,“從海到陸,由海制陸”等海戰思想也在快步發展,都需要艦炮裝備在對海對岸作戰時,具備遠程精確打擊與持續火力支援能力。艦炮制導炮彈不僅比導彈射速高、效費比高、持續作戰能力強,而且較常規彈藥射程遠、脫靶量小,能夠對近岸目標實施遠程壓制與精確打擊,為登陸部隊提供持續可靠的火力支援。

導引控制系統是關系到艦炮制導炮彈實現作戰目標的關鍵,它的常規設計方法是基于時標分離條件,忽略兩子系統之間的耦合作用,難以證明整體制導系統的穩定性。但隨著攻防裝備升級、彈目相對運動加劇,質心導引與姿態控制之間的耦合作用顯著增強,將兩個子系統進行導引控制一體化(integrated guidance and control, IGC)設計,能夠進一步提升制導系統的整體性能。

Williams等最早在1983年提出IGC,通過氣動角來聯系質心導引與姿態控制,集成出一個高階串級系統,根據彈目相對運動、彈體姿態等信息直接解算出舵機的操縱指令。隨著現代控制理論的蓬勃發展,涌現出最優控制、反步控制、動態面控制、滑模控制(sliding mode control, SMC)等IGC設計方法。

應用最優控制進行IGC設計的難點是求解Hamilton-Jacobi-Bellman方程,Vaddi等基于Riccati方程實現了IGC數值求解,但計算量大。Xin等基于θ-D方法成功地進行了IGC次優化設計,其性能卻敏感于指標權重。針對飛行器IGC設計問題,Seyedipour等提出了一種反步控制方法,通過Lyapunov理論分析了系統穩定性。針對導彈IGC系統,Ibarrondo等基于反步控制完成了IGC設計,該方法的主要缺陷是,在解算虛擬控制量的時候容易造成微分膨脹問題。為此,Wang等在進行導彈縱平面IGC設計時,運用低通濾波器進行求解,有效地避免了微分膨脹現象的出現。Guo等針對攔截彈IGC設計中存在的噴流擾動,運用動態面控制有效減弱了控制量峰值。響應速度快、實踐難度小、系統穩定性強等是SMC的顯著優勢,Jiang等基于一階滑模提出了IGC設計方法,運用視線角與視線角速率構造滑模面。Koren等研究了導彈攔截機動目標時的IGC設計問題,提出了無需目標機動先驗信息的一階SMC方法,具有一定的實際應用潛力。Sagliano等基于高階滑模設計了飛行器IGC控制指令,在一定程度上提升了制導系統的整體性能。同時,作用于系統內、外部的不確定性干擾,無疑對IGC設計施加了更多的壓力。因此,Wang等運用擴張狀態觀測器(extended state observer, ESO)精確地估計出未知干擾,提高了IGC系統的魯棒性。ESO由Han首次提出,可以迅速準確地觀測出不確定性干擾，值得一提的是,它并不需要研究對象準確的數學模型。進一步地,Wang等將IGC設計轉化為狀態變量的跟蹤問題,設計ESO估計目標機動,但未將ESO的觀測誤差納入到系統穩定性分析當中。

在實際作戰中,為了提升對目標的毀傷效果,往往會要求彈體以一定的攻擊角命中目標;制導炮彈區別于導彈等的最大特征,就是發射后始終處于自旋狀態,這限制了視線角速率的測量,上述約束條件顯然向IGC設計提出了新的挑戰,尤其是在同時還要兼顧系統一致最終有界(uniformly ultimately bounded, UUB),而這些恰恰是客觀存在且亟待解決的重要問題。值得注意的是,相對于導彈等高速飛行器,制導炮彈只采用電動舵機作為唯一的執行機構,而齒隙是制約舵機性能的重要非線性因素,但在上述文獻中,均是將舵機視為低階的理想模型,難以反映出實際存在于舵機中的非線性特性與動態特性對飛行控制的影響程度,因此在設計IGC方法時考慮舵機齒隙具有重要的意義。

然而,齒隙死區模型具有非連續、不可微等非線性特性,并且重要的參數通常也很難精確測量出來,這在一定程度上阻礙了齒隙模型建立與精確補償控制,于是諸多學者先后提出了包括逆模型、遲滯模型等在內的一些齒隙非線性模型。但是在舵機三閉環控制系統中,齒隙很難直接折算到控制指令的輸入端,這限制了逆模型的推廣與應用,另一方面,遲滯模型雖然具有結構簡單的優勢,但它是不可微的,容易導致傳動力矩在換向時發生震蕩。為了能夠對其進行高精度的逼近,文獻[30]設計了一種便于系統控制的近似死區模型,它具有連續可微的性質,文獻[31]進一步闡明了采用該模型描述齒隙的合理性與可行性,并分析論證了參數選取與逼近精度的關系。

本文綜合考慮了多項約束與齒隙因素,基于動態面滑模(dynamic surface sliding mode, DSSM)控制與Lyapunov穩定性理論,提出了考慮齒隙的多約束導引控制一體化(IGC with multiple constraints and backlash， IGCMCB)方法。需要解決下列幾項問題:首先,針對不確定干擾與視線角速率難以測量,要設計ESO對其進行實施準確迅速的觀測,并將觀測誤差納入到系統穩定性分析中;然后,為了在有限時間內零化視線角跟蹤誤差與視線角速率,需要結合彈目距離與接近速率,設計具有自適應指數趨近律的非奇異終端滑模,并且運用DSSM消除控制量的高頻抖振;最后,IGCMCB不僅需要使制導炮彈滿足多項約束條件和全系統狀態UUB,同時也應該有效地削弱齒隙對于IGC設計的影響。

1 模型建立

1.1 IGC設計模型

在縱平面中,構建制導炮彈IGC設計模型,示意如圖1所示。

圖1 制導炮彈的IGC設計模型Fig.1 IGC design model of guided projectile

圖1中,表示艦炮制導炮彈,為目標,、、、、、分別為基準系、彈體系、彈道系、視線系、目標基準系、目標彈道系,、與、表示彈體和目標的速度、彈道傾角,、、、、、分別表示彈目距離、視線角、俯仰角、攻角、舵偏角、水平風速,2、2表示彈體加速度在系的分量,8、8表示目標加速度在系的分量。為便于分析討論,作以下合理假設:

視目標為質點,、、均易通過成熟途徑獲取,且始終滿足>。

彈目相對運動關系為

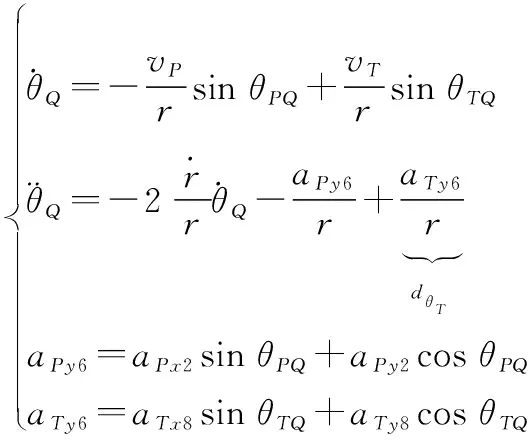
(1)

式中:=-；=-；為目標機動引入的干擾；2、2分別表示為

(2)

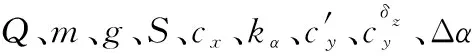
在縱平面內,彈體動力學方程為

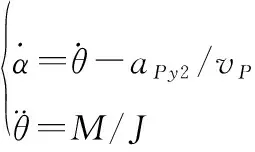
(3)

式中:、表示俯仰力矩、轉動慣量,其中,為

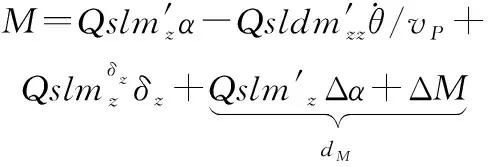
(4)

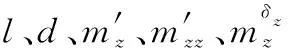
升力主要由產生,將由產生的升力視為有界不確定干擾。

根據文獻[14],可以將攻擊角視為在彈體命中目標時,彈體速度與目標速度之間的夾角,并且約束可以等價地轉換為對的終端值的約束。

1.2 含齒隙的雙慣量舵機模型

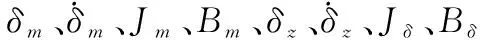
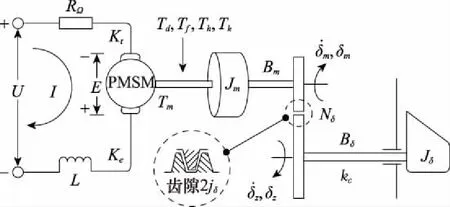
圖2 含齒隙的舵機雙慣量模型Fig.2 Double inertia model of canard with backlash

該模型可由如下傳動力矩方程描述:

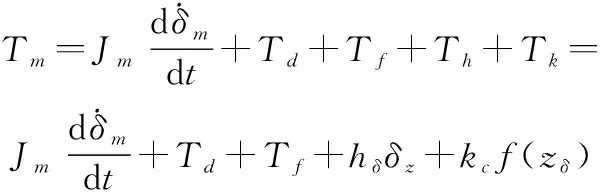
(5)

式中:=max為鉸鏈矩系數,max為舵機最大力矩;=-為驅動、從動軸之間的相對轉角,即齒隙寬度,且有-2≤≤2;()為連續不可微的死區函數。為了便于設計,引入連續可微的近似死區函數:

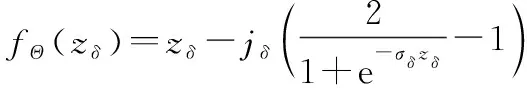
(6)

記()與()的逼近誤差為Δ()。

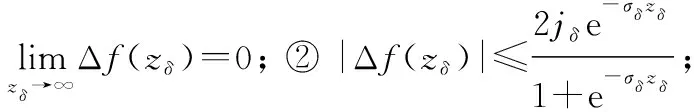
彈載舵機的電機伺服系統采用三閉環控制方式,同時,引入含有非線性齒隙的舵機雙慣量模型,記、、分別表示電流、速度、逆變器的比例控制系數,為位置控制器輸出的控制信號,為速度環反饋系數。

1.3 近岸目標模型

近岸目標可以由一階慣性環節描述:

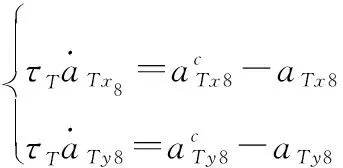
(7)

1.4 系統狀態空間模型

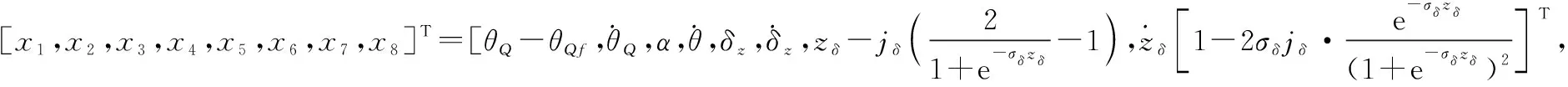
(8)

式中:=e-(1-e-)(1+e-)；=1-2e-(1+e-)。為了便于分析討論,根據系統實際情況,作合理假設如下:

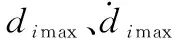
Δ()在定義域上屬于連續函數,當且僅當=±時不可導,原因是左導數不等于右導數,但在除此以外的定義域上,均可導,并且導數有界。

2 IGCMCB設計

設計方法目的為針對含舵機齒隙雙慣量模型的IGC系統式(8),在約束、測量受限、(=2,3,4,6,8)未知有界的工況下,得到適宜的控制量,在有限時間內零化、,確保系統UUB,迅速穩定地收斂至平衡點附近充分小的鄰域內。

設計方法IGCMCB結構原理如圖3所示,主要由ESO、非奇異終端滑模(nonsingular terminal sliding mode, NTSM)與DSSM等構成,現分別對它們進行設計,隨后再進行閉環系統的穩定性分析。

圖3 IGCMCB的結構原理示意圖Fig.3 Schematic diagram of IGCMCB structure and principle

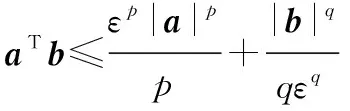
2.1 ESO設計

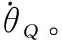
(9)

式中:0<<<；0<<<1；0<2<1(=1,2)；非線性函數fal為

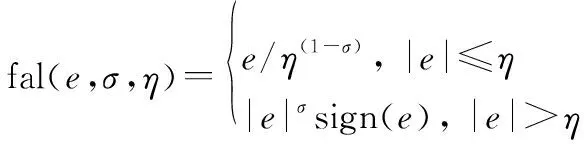
(10)

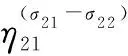
進一步化簡式(9),可得觀測誤差的動態方程組為

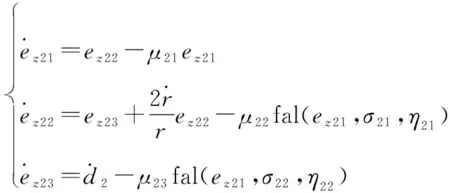
(11)

式中:fal為分段非線性函數,顯然需要分情況進行討論,當<|21|時,有等式fal(21,,)=|21|sign(21)成立,結合等式21=|21|(1-)|21|sign(21),式(11)可化簡為

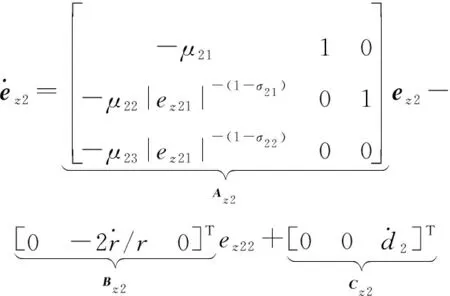
(12)

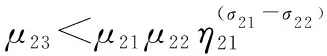
(13)

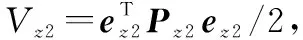
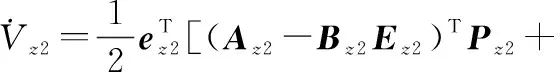
(14)

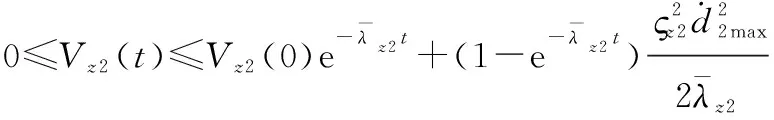
(15)

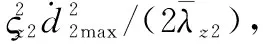
證畢

為了迅速準確地觀測出不確定性干擾(=3,4,6,8),定義觀測變量、,定義觀測誤差為1=-、2=-,分別設計二階ESO為

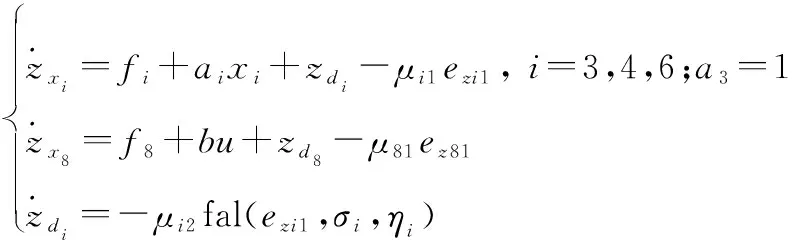
(16)

式中:各參數定義、取值范圍以及函數形式參照ESO模型式(9)。

2.2 NTSM設計

為保證系統狀態收斂的快速性,同時避免奇異問題出現,設計NTSM為

=+||sign(), 0<；1<<2

(17)

對式(17)求導可得

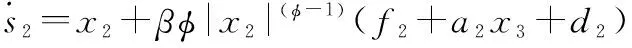
(18)

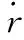
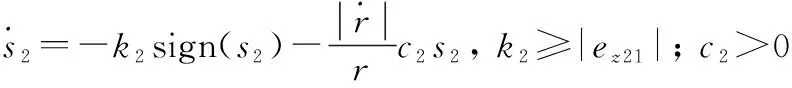
(19)

聯立式(8)和式(9),并舍棄奇異因子||(1-)(),推導虛擬控制量3為

(20)

針對系統式(8)前兩個等式構成的子系統,采用ESO模型式(9)與NTSM模型式(17)和式(19),通過選擇合適的參數,則能使系統狀態、在有限時間內收斂至零。

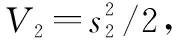
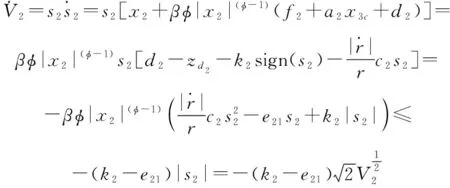
(21)

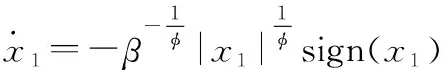
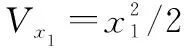
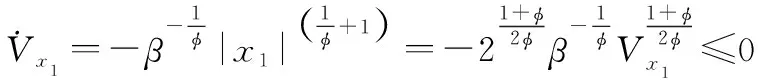
(22)

根據引理2,、可以在有限時間內收斂至零。

證畢

2.3 DSSM設計

系統式(8)屬于高階非線性系統,為了對其進行有效的鎮定,并且避免反步法產生的微分膨脹問題,需要運用DSSM進行方法設計。

設計3使→0,通過一階濾波器得到3,其有時間常數:

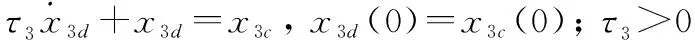
(23)

定義動態面3為=-3,求導可得

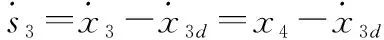
(24)

設計DSSM的指數趨近律為

(25)

同理,設計動態面4～8分別為

=-，=4,5，…,8

(26)

式中:為虛擬控制量的濾波值,設計與控制量分別為

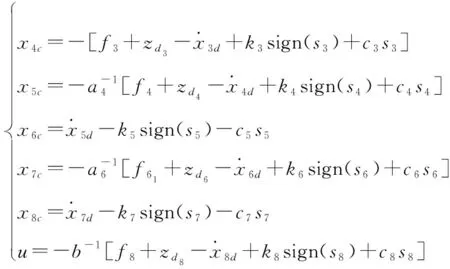
(27)

式中:|1|≤(=3,4,6,8),0≤,0≤,0<(=3,4，…,8),為避免對(=3,4，…,8)直接求導而產生微分膨脹問題,設計一階濾波器為

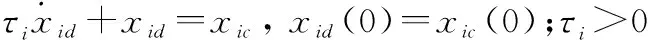
(28)

至此,IGCMCB設計完畢,由ESO模型式(9)和式(16),NTSM模型式(17)和式(20),DSSM模型式(23)～式(28)組成。

IGCMCB中的(=2,3,…,8)為滑模切換項增益,與其對應的符號函數共同組成滑模切換項,作用是抑制不確定干擾并保證系統快速穩定,而||(2-)()雖然也帶有符號項,但它僅僅是由NTSM引入的附加切換項。

3 穩定性分析

定義虛擬控制量誤差為

=-，=3,4，…,8

(29)

進行求導,可得

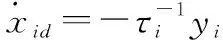
(30)

進一步推導,可得

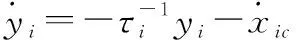
(31)

=++

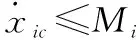
(32)

選取閉環系統Lyapunov函數為

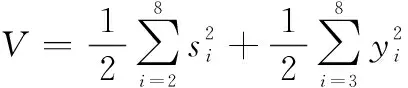
(33)

對于系統式(8),采用IGCMCB設計方法,通過選擇合適的參數,則能夠使閉環系統UUB,并且能夠迅速穩定地收斂至平衡點附近充分小的鄰域內。

對全系統Lyapunov函數式(33)進行求導,并結合上述分析,推導可得

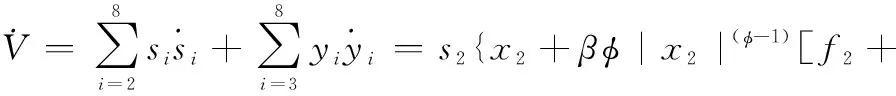
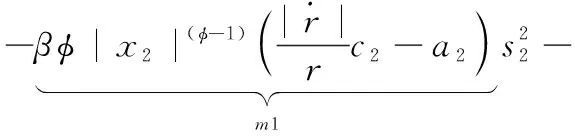
(34)

為了保證系統穩定,在選取參數時需要滿足以下條件:

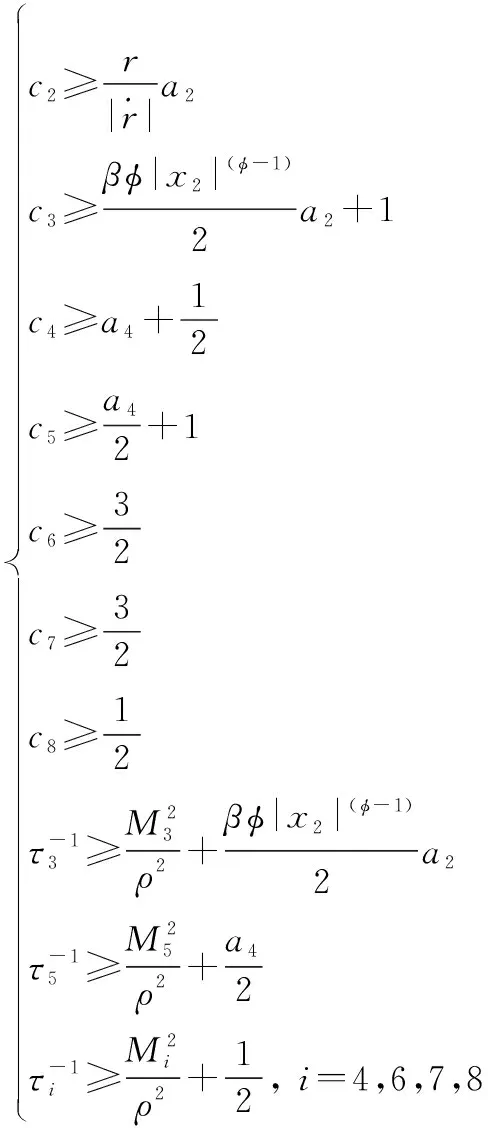
(35)

令正常數=min{(=1,2,…,13)},則式(34)可以進一步化簡為

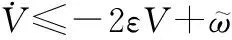
(36)

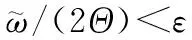
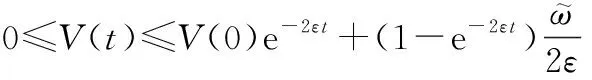
(37)

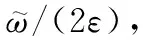
證畢

盡管式(35)給出了保證系統穩定性的參數選取范圍,但由于受到多方面因素的約束,例如,在提高系統收斂速度的同時,需用過載往往容易超過可用過載,因此給出設計參數的具體定量選擇標準是比較困難的。目前常采用的方法是綜合考慮設計方法與實際物理環境,再通過大量的數學仿真來進行定量選擇。

為了便于定理3的推導證明,在中并未包含ESO模型式(9)和式(16)的觀測誤差項,但結合定理1可知,當中涵蓋這些ESO觀測誤差項時,定理3是同樣成立的。

4 仿真實驗

本節的主要目的是分別在目標固定與蛇形機動的工況下,通過數學仿真對IGCMCB進行分析與驗證。微分方程組解算方法采用4階Runge-Kutta,步長10 ms。仿真環境、彈體、舵機以及IGCMCB的參數設置分別如表1～表4所示。

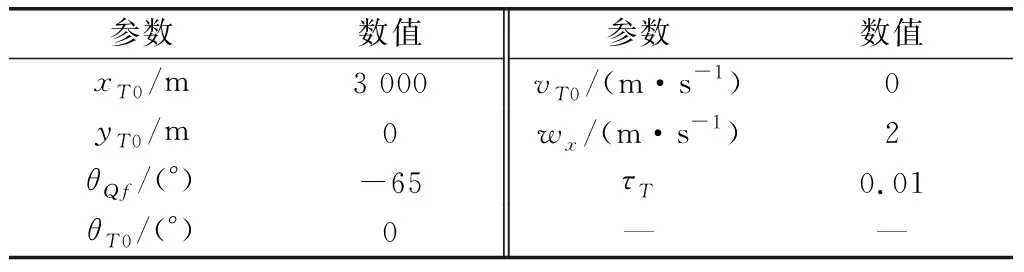
表1 仿真環境參數Table 1 Simulation environment parameters

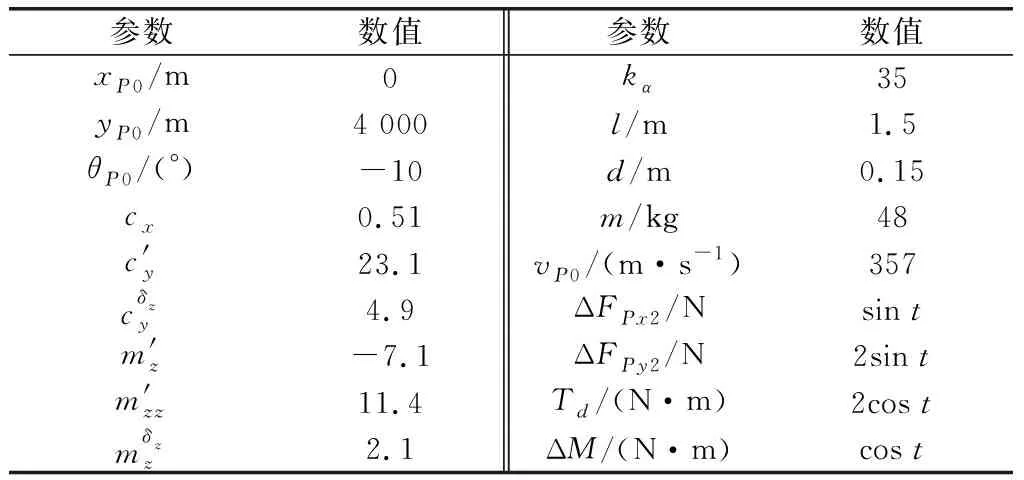
表2 彈體參數Table 2 Projectile parameters

表3 舵機參數Table 3 Canard parameters

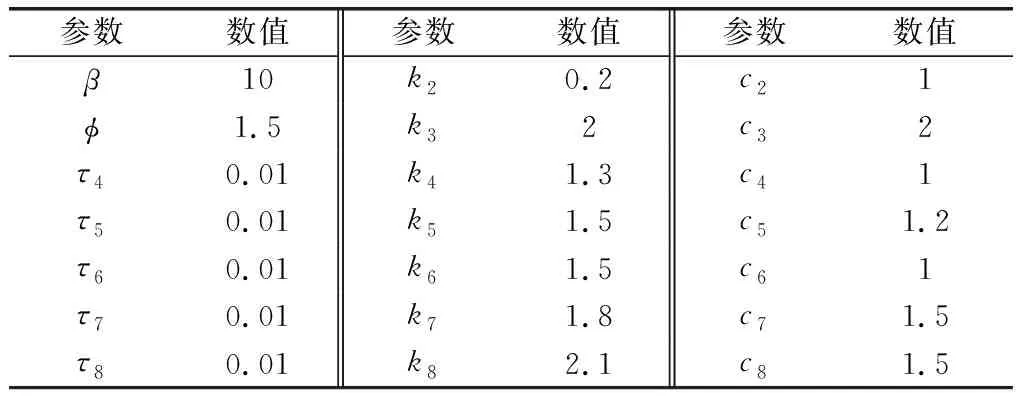
表4 IGCMCB參數Table 4 IGCMCB parameters

表1～表3中下標“0”表示參數初值。根據在第1節中建立的設計模型可知,、2、2、等是由其他已定義變量構成的,因此僅需要給出Δ2、Δ2、Δ、、等項的數值,以便于定量分析干擾項。

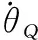
為了探究舵機齒隙對于IGC設計的影響,同時又能夠體現出IGCMCB抑制齒隙的有效性,引入自適應動態面控制(adaptive dynamic surface control, ADSC)作為對比,含齒隙舵機部分采用PID控制,簡記為ADSC&PID。

4.1 工況1:固定目標

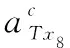
表5 工況1的仿真實驗結果Table 5 Simulation results of condition 1

圖4 工況1仿真實驗曲線Fig.4 Simulation curves of operating condition 1

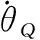
4.2 工況2:蛇形機動目標

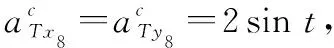
表6 工況2的仿真實驗結果Table 6 Simulation results of condition 2

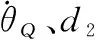
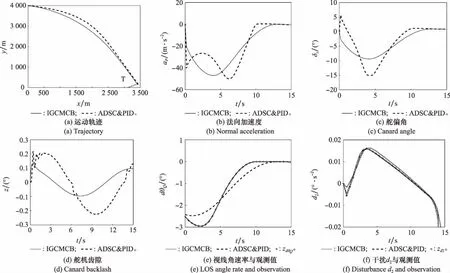
圖5 工況2仿真實驗曲線Fig.5 Simulation curves of operating condition 2

5 結 論

針對艦炮制導炮彈在實施對岸遠程火力支援的末段,考慮齒隙、約束攻擊角以及測量視線角速率受限,基于DSSM與ESO設計了IGCMCB,主要從構建模型、方法設計、系統穩定性分析以及仿真實驗等4個方面展開了詳細的研究,現總結全文如下:首先,設計了ESO準確迅速地估計出視線角速率與各類干擾,分析了由觀測誤差所組成系統的穩定性,為導引控制提供了關鍵必要信息;然后,結合彈目距離與接近速率,設計了具備自適應指數趨近律的NTSM,在有限時間內零化了視線角跟蹤誤差與視線角速率,運用DSSM成功地避免了控制量高頻抖振;最后,IGCMCB使制導炮彈在滿足多項約束和系統UUB的同時,有效地削弱了齒隙對IGC設計的影響,所需信息均可通過成熟技術途徑獲取,具有一定的理論意義與應用價值。