HEC?HMS 模型在岢嵐流域的應用研究
梁彥寬,祝雪萍,孫小平,牛永華,武鵬林,張 宇
(1.太原理工大學 水利科學與工程學院,山西 太原 030024;2.山西省水利水電科學研究院,山西 太原 030002)
1 概 況
HEC?HMS 模型是美國陸軍工程師團水文工程中心開發的一個基于物理機制的半分布式水文模型。 該模型充分考慮了降雨時空分布不均勻性和流域下墊面空間變異性,可以更好地反映產匯流規律,在中小流域有很好的適用性[1]。 HEC?HMS 模型克服了概念性流域水文模型在產流、坡面匯流、基流與河道匯流計算方面的單一性,提供了多種模擬方法,可根據實際情況進行優化組合,提高模擬計算的效率和精確度;同時具有一系列強大的水文模擬功能,能夠模擬不同時間尺度的降雨徑流過程,在洪水預警系統中得到了廣泛應用[2-4]。 趙彥增等[5]介紹了HEC?HMS 模型對于不同流域特征、不同資料情況下的不同計算方法,同時指出模型可用于無資料山丘區的山洪預警預報。 袁玉等[6]構建了秦淮河流域考慮圩垸的HEC?HMS 模型,通過對降雨徑流過程模擬,分析比較了有、無圩垸的防洪模式對洪水演進的影響。 Silva 等[7]研究了HEC?HMS 模型在Kelani 河流域的適用性,并提供了山洪災害防治過程中必要的洪水預警信息。
岢嵐流域位于山西省岢嵐縣,流域面積476 km2,岢嵐水文站以上主河道長度為43.8 km,主河道平均比降為0.71%,流域形狀系數為0.248。 流域內分布有5 個雨量站,1 個控制性水文站即岢嵐水文站[8]。 岢嵐流域地處黃河流域,屬于半干旱半濕潤地區,是典型的山區小流域,蓄滿產流和超滲產流兼有,產匯流規律復雜。本文針對岢嵐流域分別采用SCS 曲線法計算流域產流、SCS 單位線法計算坡面匯流、指數衰退法計算基流、馬斯京根法計算河道匯流,選取岢嵐流域1967—2007 年14 場洪水,以15 min 為步長,對HEC?HMS 水文模型在岢嵐流域的適用性進行研究,旨在為山西省典型小流域洪水預報提供借鑒。
2 研究方法與模型構建
2.1 研究方法的選取
2.1.1 產流計算——SCS 曲線法
HEC?HMS 模型有多種可用于產流計算的方法,其中SCS 曲線法具有計算過程簡單、參數少、所需資料易于獲得的特點。
SCS 曲線法是一種用于計算流域降雨損失的方法,也叫SCS?CN法,其最大的特點是引入了無因次參數CN。該參數與流域的累計降雨量、土地利用情況、土壤類型等空間分布數據密切相關,并會隨其變動而改變參數取值。此外,參數CN的引入建立了土壤最大蓄水量S與流域特征之間的關系,簡化了產流計算的步驟,大大提高了計算流域產流量的效率。 相關計算公式如下:
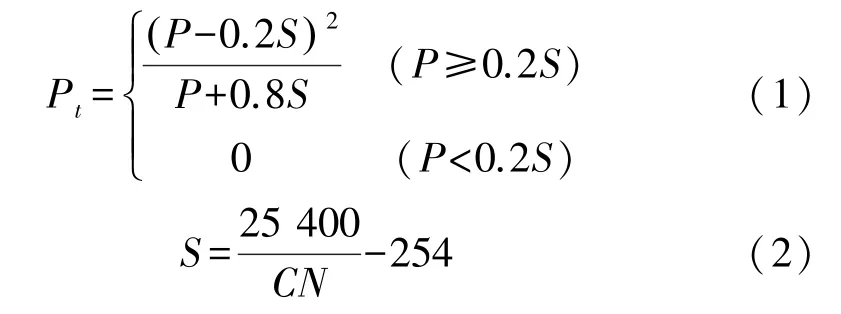
式中:Pt為時間t時的流域產流量,mm;P為時間t時的降雨量,mm;S為土壤最大蓄水量,mm;無因次參數CN取值范圍為0~100,在實際洪水模擬中,常用取值范圍為30~100。
2.1.2 坡面匯流計算——SCS 單位線法
SCS 單位線是一個無量綱單峰的單位線,模型主要涉及一個參數,即流域滯時(Lagtime)。 計算原理是用一個系數與單位線峰值流量Up和單位線峰現時間Tp作乘法運算,得到任意時間t的單位線流量Ut。
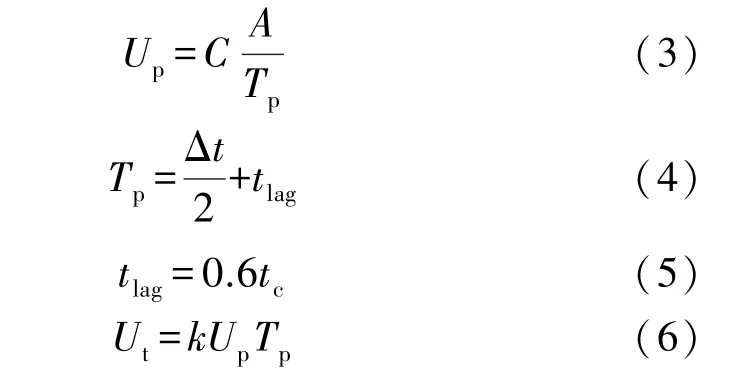
式中:k為無量綱系數;C為轉化常數;A為集水面積;tlag為流域滯時;tc為匯流時間(一般為坡面徑流、壤中流、河道徑流時間之和)。
2.1.3 基流計算——指數衰退法
指數衰退是指基流從流量的初始值開始以指數的方式衰減,常用來表示集水區蓄水量的自然排水過程。在HEC?HMS 模型中基流計算模塊涉及初始基流量、衰減系數和峰值比3 個參數。t時刻的基流可表示為

式中:Qt為t時刻的基流量;Q0為初始基流;b為衰減系數。
2.1.4 河道匯流——馬斯京根法
在HEC?HMS 模型用于河道匯流的方法中,馬斯京根法最常用,且參數率定精度高。
馬斯京根法是河道流量演算方法的一種,有兩個重要的模型參數,一是槽蓄曲線坡度K,另一個是流量比重因子x。 河道流量演算方程如下:

式中:I1、I2分別為河段起、止時刻上斷面入流量;Q1、Q2分別為河段起、止時刻下斷面出流量。
2.2 模型的構建
通過ARCGIS 中地理空間水文模型擴展模塊HEC?GeoHMS 對岢嵐流域的數字高程DEM(見圖1)進行填洼、河網提取、流域特征提取、子流域劃分等一系列水文分析,借助土地與土壤資料對岢嵐流域進行土地利用與土壤類型分析,基于泰森多邊形方法求出各雨量站的面積權,完成岢嵐流域數字模型的構建[9]。 結合上文提到的4 種研究方法的選取,最終建立岢嵐流域HEC?HMS 水文模型,見圖2。 模型將岢嵐流域劃分為7 個子流域,編號分別為W80、W90、W100、W110、W120、W130、W140;3 條主干河道,編號分別為R20、R30、R40。 各子流域控制雨量站權重見表1,各子流域特征值見表2。

表1 各子流域控制雨量站權重值
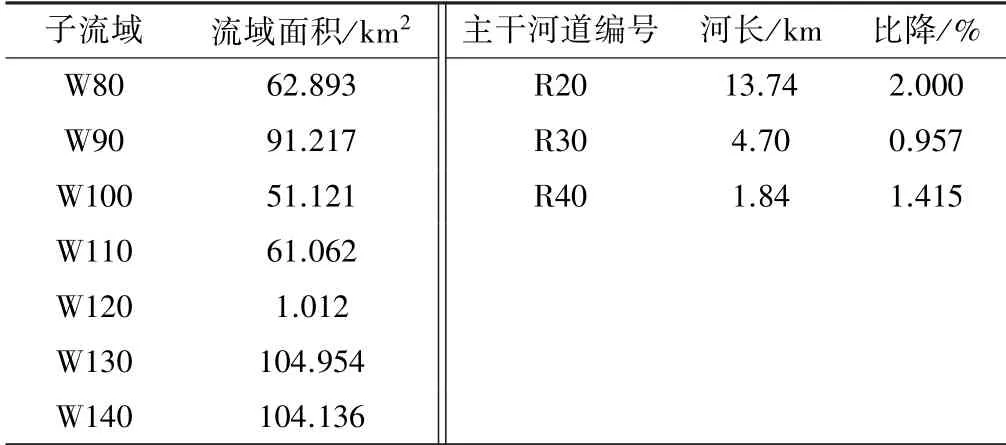
表2 岢嵐流域子流域特征值統計
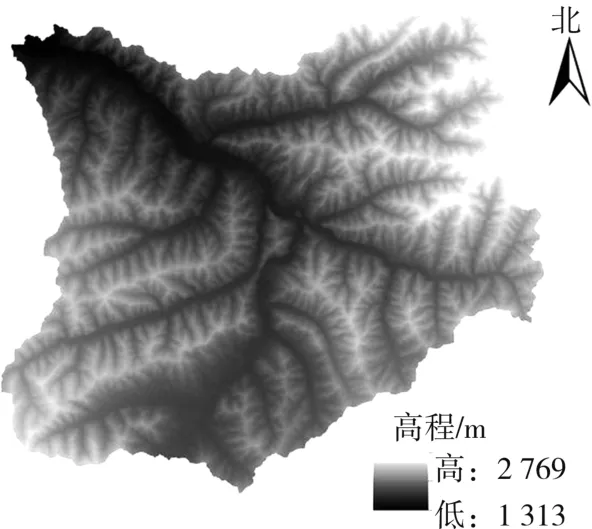
圖1 岢嵐流域數字高程DEM
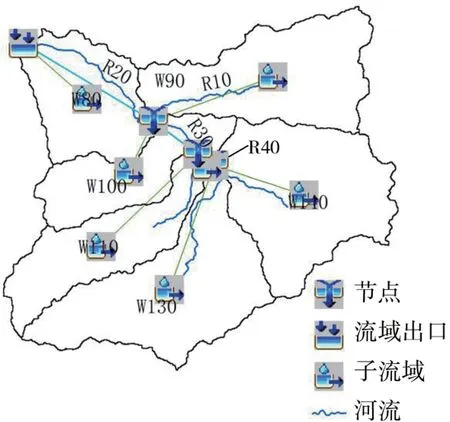
圖2 岢嵐流域HEC?HMS 模型概化
3 HEC?HMS 模型在岢嵐流域的應用
3.1 HEC?HMS 模型的應用
基于岢嵐流域1967—2007 年洪峰流量長時間序列進行頻率分析,并據此劃分洪水類型[10],劃分結果見表3。

表3 岢嵐流域洪水類型劃分結果
選取歷史洪水中具有代表性的降雨-徑流場次洪水共14 場,以步長為15 min,并應用HEC?DSSvue 軟件將降雨-徑流數據轉換格式,匹配HEC?HMS 模型使用。 按時間順序選取前7 場場次洪水進行率定,后7場場次洪水進行驗證,結果見表4。
3.2 HEC-HMS 模型的應用結果
根據表4 可知:
率定期7 場洪水中洪峰流量均在允許誤差20%范圍內,峰現時間均在允許誤差2 h 以內,徑流總量均在允許誤差20% 范圍內,但編號19670803 與編號19690726 場次洪水DC值未能達到合格,所以率定期共有5 場合格,合格率為71.4%,模擬效果較好,模擬結果達到了乙級精度。
驗證期7 場洪水中洪峰流量均在允許誤差20%范圍內,峰現時間均在允許誤差2 h 以內,徑流總量均在允許誤差20% 范圍內,但編號19930729 與編號20070630 場次洪水DC值未達到合格,所以驗證期共有5 場合格,合格率為71.4%,模擬效果較好,模擬結果達到了乙級精度。
在岢嵐流域模擬的共14 場場次洪水中,所有場次的洪峰流量、徑流總量及峰現時間均在允許誤差范圍內的合格率為100%;DC平均值為0.625,DC值大于0.7 的有8 場,大于0.6 的有10 場,小于0.5 的有4 場。綜合考慮,合格率為71.4%,模擬效果較好。 根據《水文情報預報規范》[10]中預報精度等級劃分標準(見表5),模擬結果達到了乙級精度,預報方案可用于研究區的洪水預報。

表5 洪水預報精度等級劃分[10]
根據模擬洪水類型可以看出,14 場洪水中有6 場小型洪水、6 場中型洪水、1 場大型洪水、1 場特大型洪水。 其中:小型洪水徑流量相對誤差均小于20%,合格率為100%,總體合格的有5 場,合格率為83.3%,達到甲級精度;大中型(包括特大型)洪水合格的有5場,合格率為62.5%,達到丙級精度。 由此可見,本文建立的岢嵐流域HEC?HMS 洪水預報模型,針對小型洪水的模擬精度較大中型洪水的模擬精度更高,因此在研究區實際洪水預報中,小型洪水預報結果較可靠,大中型洪水預報結果可作為參考性預報。
4 結語
(1)運用HEC?HMS 模型對岢嵐流域的降雨徑流過程進行模擬,將洪峰流量、峰現時間、徑流總量和確定性系數作為判斷指標,率定期與驗證期合格率均為71.4%,均達到了乙級精度,說明該模型在岢嵐流域模擬效果較好,可用于岢嵐流域洪水預報。
(2)根據14 場洪水的模擬結果可知,HEC?HMS模型在岢嵐流域內小型洪水的模擬精度相較于大中型洪水的模擬精度高,在未來研究區實際洪水預報中,小型洪水預報結果較可靠,大中型洪水預報結果可作為參考性預報,具體原因還需深入分析與探索。
(3)下一步研究需對HEC?HMS 模型在岢嵐流域降雨徑流過程模擬時的參數進行敏感性分析與影響機制研究等。

