板狀結構自發大變形問題的三維數值分析1)

張默涵 李錄賢

(西安交通大學航天航空學院機械結構強度與振動國家重點實驗室,西安 710049)

(西安交通大學飛行器環境與控制陜西省重點實驗室,西安 710049)

引言

自然界中的物體有著豐富多彩的形貌,其中又以樹葉、花朵、海帶等板狀結構最具代表[1-4].板狀結構是指完全相同的面狀結構在厚度方向堆砌而形成的厚度尺寸比面內尺寸相比較小的一類特殊三維結構[5].與一般三維結構相同的是,板狀結構因內部生長或外部環境等因素也存在內部應力,并通過文獻[6-7]沿葉片主脈方向等間距切割樹葉的實驗得到了證實.但與一般三維結構不同的是,板狀結構更易通過變形模式轉變釋放內部應力而具有復雜的平衡構型[8-9],例如大豆的豆莢在張開后具有螺旋扭曲的形狀[10-11],這正是板狀三維結構的特殊之處.

從能量角度考察,板狀結構的變形遵守系統總能量最小原理;從形貌角度考察,因總是選取剛度較小、易于變形的模式,板狀結構常常形成更復雜的形狀,這正是大自然中花朵和樹葉具有迷人而復雜圖案的物理機制[12].該機制可為工業設計和制造提供新的靈感:文獻[13-14]通過釋放柔性板狀結構的預應變分別得到形狀復雜的器官芯片和各類特定形狀的飛行器;文獻[15-16]通過外界刺激使水凝膠制成的板狀結構內部發生不均勻變形,進而驅動水凝膠運動;文獻[17]通過釋放粘接在一起的雙層板狀結構因變形不同而產生的內部應力制備了納米管.這種機制還可解釋生物生命活動中的許多現象,例如團藻內細胞片的內陷[18]、人類雙眼皮的形成[19]等.

自然界和人工系統中許多物體的變形特征是,在無外界載荷作用或幾何約束時,結構受內部存在的不協調幾何因素激發而發生自發大變形[5,20],同時產生殘余應力.該問題是一個經典的非協調彈性力學問題,為此發展了三種基本理論[21]:第一種理論是將殘余應力處理為一個物理場、并表征其特性;第二種理論是將變形梯度分解為生長或外部環境引起的不協調變形梯度與彈性松弛變形梯度之積;第三種理論是將應變分解為生長或外部環境引起的不協調應變與彈性應變之和.由于大變形問題的非線性和三維問題的復雜性,借助于有限元方法優勢的數值分析可望成為該類問題求解的一種有效途徑.

實際上,板狀結構因厚度尺寸比面內尺寸明顯較小,一般將其轉化為薄板問題加以研究.例如,Efrati 等[20]采用曲線坐標系,以目標度量張量描述薄板局部無應力時的期望距離,度量張量g描述變形后結構的實際距離,推導了“不協調彈性理論”,并經退化建立了非歐板理論.但是,由于曲線坐標系的引入及內部應力場分布的復雜性,運用板理論可以求解的板狀結構自發大變形問題僅限目標度量張量為簡單圓錐曲線函數[5,20]的幾個實例.

本文借助于有限元分析,對板狀結構的自發大變形問題進行研究.

1 基本理論

1.1 自發大變形問題描述

對于因生長、外部環境等因素而具有內部應力的板狀結構 Ω,建立如圖1 所示的笛卡爾坐標系統,其中o-x-y為板狀結構的中面,z為板狀結構的離面方向.結構的上下面均自由;側面邊界 Γ 分為給定位移(本質) 邊界條件u(x,y,z)=u0(x,y) 的邊界 Γu和零外力(自然) 邊界條件 σij(x,y,z)nj(x,y)=0 的邊界ΓS,其中 σij為柯西應力,nj為板狀結構側面的外法向余弦.另外,板狀結構內部還存在一個沿厚度不變的初始不協調應變場(x,y),它是結構發生自發大變形而產生內部應力的動因,也是本文所研究自發大變形問題的特色.對于邊界 ΓS上沿厚度方向作用非零外力 σij(x,y,z)nj(x,y)=ti(x,y) 的情形,可等效為相應內部應力場產生的自發大變形問題加以研究.

圖1 板狀結構及坐標系統Fig.1 A plate-like structure and the coordinated system

其中Vi j為左柯西-格林變形張量.

結合柯西應力場 σij(x,y,z),結構變形能E可表示為

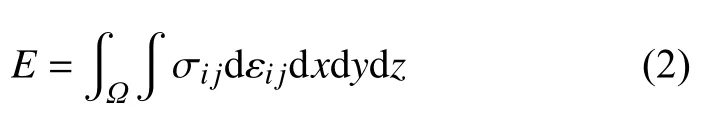
本文研究的自發大變形問題,是一個典型的大撓度、小應變問題,根據文獻[23],材料仍服從胡克定律,本構關系可表示為

其中G=Y/(1+2ν)和λ=νY/[(1+ν)(1-2ν)] 為拉梅常數,Y和ν 為材料的楊氏模量和泊松比.

由于無外力做功,結構的總勢能等同于系統的變形能,于是,結構將在變形能最小原理支配下發生自發大變形.對于這樣一個非線性三維大變形問題,本文運用有限元方法加以分析.

1.2 板狀結構的特性分析

1.2.1 板狀結構的變形模式分析

為了說明板狀結構可能的變形模式,考察面內尺寸為 2L、厚度為h的方形板狀結構.假定從中切出邊長為L的方形塊,這樣就形成一個U 型結構,如圖2(a).接下來,在方形槽中插入一個材料相同,三邊長為L、第四邊(外邊)長為L0(＞L) 的梯形塊,使邊長為L的三邊與U 型結構的相應邊粘在一起.這樣,U 型結構會因L0＞L而張開,同時梯形塊將受到壓縮,如圖2(b)所示;但是,如果板狀結構足夠薄,梯形塊將不再保持面內的壓縮變形模式,而是彎曲成如圖2(c)所示的形狀[20].

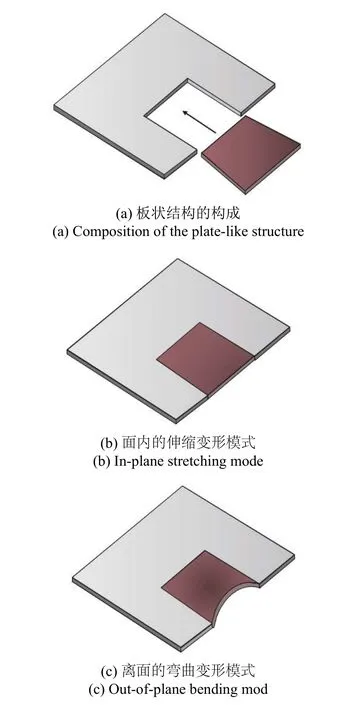
圖2 板狀結構及其變形模式Fig.2 A plate-like structure and its deformation modes

上述分析表明,存在內部應力的板狀結構,具有兩種可能的變形模式:一種是面內的伸縮模式,其特征是沿板厚度方向的每一個平面都相同,在厚度方向保持上下對稱;另一種是離面的彎曲模式,其特征是上下表面之其一發生伸長、而另一則發生收縮,在厚度方向不再上下對稱.可以看出,該結構的變形由于梯形塊與正方形空槽間的幾何不協調而產生,而變形模式則與結構的厚度密切相關.

1.2.2 板狀結構的變形能分離

當厚度h較小時,通過引入Kirchhoff-Love 假設,板狀結構可轉化為板問題加以研究,例如F?ppl-Von Kármán 板理論[24]、Koiter 板理論[23]等.這些板理論均表明,大變形時板狀結構的變形能E可分離為伸縮變形能Es和彎曲變形能Eb之和,即

薄板彎曲時,伸縮剛度隨厚度h線性變化,伸縮能Es是中面應變的二次函數,其表達式為[25]

式(6)表明,隨著面內應變的增加,結構的撓度將經歷一個從無到有、由小到大并逐漸占主導的過程1理論上已證明[21],只有含壓縮應變問題才可誘發橫向位移.,這是薄板問題之所以發生失穩的力學機制.

薄板彎曲時,彎曲剛度隨厚度h三次變化[5,26],彎曲能Eb是中面彎曲應變的二次函數,表達式為[25]

需要說明的是,由于自發大變形過程中同時存在的面內伸縮變形和離面彎曲變形也與厚度h有關,將伸縮能表述為與厚度h成線性變化和將彎曲能表述為與厚度h成三次變化的說法(例如文獻[5,26])是不恰當的,與文獻[20]中圖3 所描述的規律也不相符.實際上,當目標度量張量對應的高斯曲率為正時,板狀結構的伸縮能和彎曲能均正比于厚度的2.5 次方;高斯曲率為負時,伸縮能則正比于厚度的4 次方[27].

圖3 正方形板狀結構的幾何尺寸Fig.3 Dimensions of the square plate-like structure

仿照薄板結構的變形能分離方法,將一般厚度板狀結構的總變形能E分離為

其中Em稱為類伸縮變形能(簡稱類伸縮能),指結構隨中面一起伸縮的變形能,Er則為除去Em的結構剩余變形能(簡稱剩余能).

利用有限元分析時,板狀結構的總變形能E為每個單元的變形能之和,即

根據定義,類伸縮能Em經結構中面的變形能計算得到,即

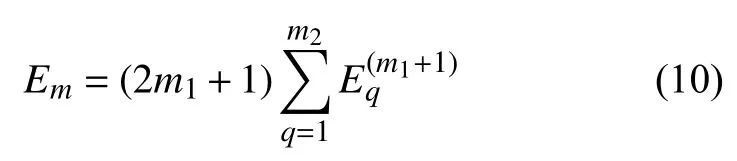
根據式(8)～ 式(10),剩余能為

隨著結構厚度h變小,板狀結構的三維變形因逐漸符合Kirchhoff-Love 假設而趨近于薄板結構的變形,此時,三維角度的Em和Er相應地就與薄板角度的Es和Eb逐漸接近.

2 自發大變形的三維分析方法

板狀結構的自發大變形行為雖然只在薄板情形下得以凸顯,但考慮到薄板結構大變形理論求解的復雜性,以及薄板結構可視為厚度h逐漸變薄的中等厚度三維板狀結構的客觀事實,本文借助于三維大變形有限元分析,提出板狀結構自發大變形問題的求解方法.

第1 節的分析已表明,板狀結構的變形能由類伸縮能Em和剩余能Er兩部分組成.本節將通過受外力作用板狀結構的三維大變形數值計算,對板狀結構的變形能構成予以定量分析,從能量角度提出屈曲失穩條件,進而揭示板狀結構失穩的力學機制.

2.1 板狀結構的三維大變形分析

如圖3 所示,考慮邊長為600 mm 的正方形板狀結構,假定前后兩邊自由、左右兩邊簡支,左端沿x方向作用沿厚度均勻分布的壓縮載荷q.選用具有三維大變形分析功能的二次縮減積分單元C3D20R,經收斂性驗證后確定沿厚度方向均勻劃分11 層,面內劃分成20×20 格,共計4400 個單元.分析時取q=228 N/mm,材料的楊氏模量Y=2.55 GPa、泊松比ν=0,計算得到不同厚度時板狀結構中心位置o點處(參考圖3)的橫向位移uz,如圖4所示.

由圖4可以看出,當厚度h＞ 8.08 mm 時,橫向位移uz很小,結構處于單一的面內伸縮變形模式;當厚度h略小于8.08 mm 時,橫向位移陡然增大,并因厚度的不同或正或負,出現分岔現象,表明結構的變形中此時增添了新的離面彎曲模式.

圖4 方板中心位置 o 處橫向位移 uz隨板厚度 h 的變化Fig.4 Variation of uzat opoint with thicknessh

2.2 變形能計算及屈曲失穩的能量條件

根據2.1 節的大變形有限元計算,利用式(9)可得到結構的總變形能E,利用式(10)可得到板狀結構的類伸縮能Em,進而利用式(11)得到剩余能Er.這樣,圖3 所示問題中類伸縮能Em和剩余能Er隨厚度的變化如圖5 所示.

圖5 方形板狀結構能量構成隨厚度的變化Fig.5 Variation of the strain energy with thickness for a square platelike structure

從圖5可以看出,在8.01 mm 至8.10 mm 較小的厚度變化范圍內,結構的總變形能大小及構成卻發生了大幅變化.當厚度h＞ 8.08 mm 時,板狀結構的剩余能Er為零,類伸縮能Em在總變形能中占主導地位,稱8.08 mm 為該結構的臨界厚度hcr,也就是說,厚度h＞hcr時,板狀結構內部不會存在彎曲變形能.

分析圖5 還發現,板狀結構存在一個類伸縮能Em與剩余能Er相同的交叉點,稱所對應厚度為變形模式轉變厚度htr,在此例中其值為8.076 mm.從三維角度,模式轉變厚度htr表征了剩余能Er和類伸縮能Em相等時的厚度,也就是說,在厚度由大變小過程中板狀結構具有類伸縮能與剩余能大小關系發生反轉的特點[21,28-29],在變形模式上表現為以面內伸縮模式為主導變成為以離面彎曲模式為主導.

與文獻[20-21]類似,基于模式轉變厚度時所表現出的能量關系,本文提出板狀結構屈曲失穩的能量條件為

對照附錄中圖A1 基于薄板經典穩定性理論中qcr=228 N/mm 對應的厚度h=8.076 mm,本文基于三維大變形數值分析得到的轉變厚度htr與之完全吻合,側證了本文分析方法及式(12)能量條件的正確性.

本節工作表明,三維大變形有限元分析是定量確定板狀結構模式轉變厚度htr的有效途徑.

3 自發大變形實例分析

運用溫度場作用下結構的熱脹冷縮效應,可有效模擬結構由于生長或外部環境引起的內部不協調變形(x,y)[30].本節運用不同種類溫度場變化,通過三維大變形有限元計算,分析板狀結構的不同自發大變形行為.

3.1 正方形板狀結構的自發大變形

如圖6 所示,考察600 mm×600 mm 正方形板狀結構.取材料的楊氏模量為2.55 GPa、泊松比為0.從中劃出一個深度300 mm、寬度為 2a的小矩形區域,設該區域作用一沿y方向線性非均勻變化的溫度場 ΔT(參考圖6),并假定材料僅在x方向具有非零的熱脹系數 α=7.5 ×10-4K-1.這樣,正方形板狀結構將在外部邊界自由、內部不協調變形作用下產生內部應力場,并因之誘發自發變形.此時,x方向正應力σx的典型分布如圖7 所示,可以看出,結構內部既有受壓(藍色)區域,也有受拉(紅色)區域.

同樣選取二次縮減積分單元C3D20R,它也具有分析溫度場作用下三維大變形問題能力.結構沿厚度方向均勻劃分11 層;將溫度作用的區域面劃分為15×15 格,共2475 個單元;其它區域在中面內劃分320 格,共3520 個單元.

首先分析厚度h對該正方形板狀結構屈曲失穩的影響.為此,假定溫度場作用的半寬度a=150 mm,令厚度h在[2.5 mm,10 mm]間每隔0.5 mm 共16 種變化,分別進行三維大變形有限元計算.

運用與2.2 節相同的技術計算結構的變形能及其構成,它們隨厚度的變化如圖8 所示.

圖8 局部溫度場作用時正方形板狀結構能量隨厚度的變化Fig.8 Variation of the strain energy with thickness due to partial change in temperature

由圖8可以看出,當板的厚度h＞ 8.5 mm 時,結構的總能量幾乎都是類伸縮能,剩余能可忽略不計,此時受溫度作用區域的變形模式為純粹的面內伸縮,此時,圖6 所示問題的臨界厚度hcr=8.5 mm.當厚度h在8.5 mm 至6.89 mm 之間變化時,總能量中剩余能的占比逐漸增加,板狀結構處于面內伸縮模式和離面彎曲模式的混合變形階段,此時,彎曲特征還不十分明顯(參考圖9(a)中的h=7.5 mm 情形).當厚度h＜ 6.89 mm 時,剩余能較類伸縮能已占據主導地位,離面彎曲特征已較為明顯(參考圖9(b)中的h=6 mm 情形),此時,圖6 所示問題的模式轉變厚度htr=6.89 mm.

圖9 局部溫度場作用下板狀結構沿厚度的變形與應力分布Fig.9 Deformed shape and stress distribution in thickness direction due to change in temperature

由圖8可進一步看出,由于與圖5 外部壓力q作用下結構內僅具有均勻單向壓應力的情形不同(參考圖7),內部不協調變形引起的結構變形能及構成變化更為復雜,臨界厚度hcr與模式轉變厚度htr不再接近,兩者相差18.9%,這也是本文采用式(12)作為屈曲失穩條件的主要原因.

其次分析溫度場作用的半寬度a對該結構屈曲失穩的影響.為此,假定板的厚度h=7 mm,令半寬度a在[100 mm,200 mm]間每隔10 mm 共11 種變化,分別進行三維大變形有限元計算.

運用與2.2 節相同的技術計算結構的變形能及其構成,它們隨局部溫度場半寬度a的變化如圖10所示.從圖可以看出,溫度作用范圍a所代表的不協調變形因素,導致結構內變形能構成的變化,也會引起結構的屈曲失穩,與改變結構厚度h的情形類似.

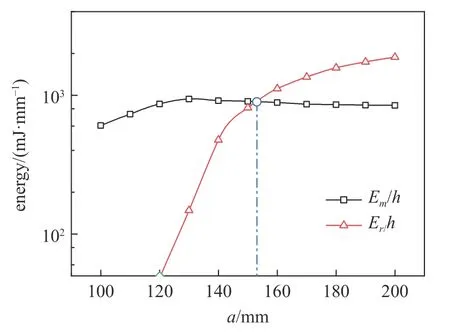
圖10 正方形板狀結構能量構成隨局部溫度場半寬度 a 的變化Fig.10 Variation of the strain energy with the half-width of local temperature in a square plate-like structure

3.2 圓形板狀結構的自發大變形

圖11 所示為半徑50 mm 的圓形板狀結構;材料為仿樹葉類PA 水凝膠彈性材料[30-31],楊氏模量為0.35 MPa、泊松比為0.25.圓形板狀結構處于沿徑向r冪律變化的溫度場 ΔT=β(r/R)n中,并假定結構僅具有沿周向的非零熱脹系數 α=1 ×10-3K-1.這樣,溫差幅值β和指數n兩個參數的變化在圓形板狀結構內將產生不同大小和分布的內部應力場,升溫和降溫時周向正應力 σθ的典型分布如圖12 所示,可以看出,整個結構中既有受壓區域(藍色)、也有受拉區域(紅色).該結構在邊界自由情形下將發生自發變形.

圖11 處于非均勻變化溫度場中的圓形板狀結構Fig.11 A circular plate-like structure subjected to a power-law change in temperature

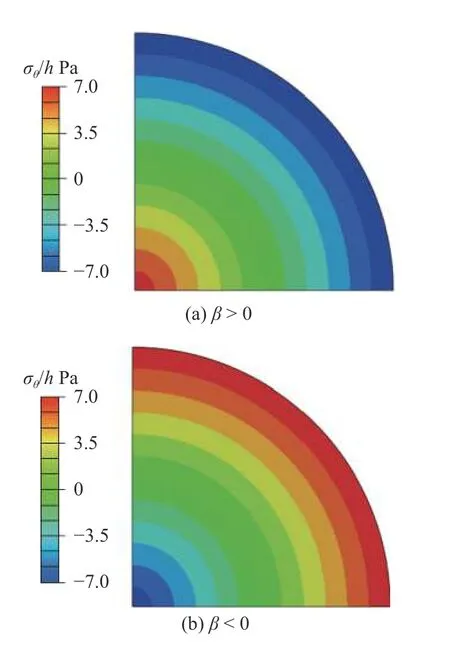
圖12 圓形板狀結構的典型周向正應力分布Fig.12 Typical distributions of circumferentially normal stresses in the circular plate-like structure

取結構的1/4 進行建模.仍選用二次縮減積分單元C3D20R,整體結構沿厚度方向均勻劃分11 層,面內劃分442 格,共4862 個單元.運用與2.2 節相同的技術計算結構的變形能及其構成,并仿圖8 得到模式轉變厚度htr,進而研究溫差幅值β和指數n兩個參數對htr的影響.

3.2.1 溫差幅值β對htr的影響

給定指數n=0.5,1,2和5,在[-5°C,5°C]間每隔1°C 共11 組β值進行計算,其中β的正負分別表示對應點處為升溫或降溫.圖13 為給定n時圓形板狀結構模式轉變厚度htr隨β的變化關系.

由圖13可以看出,模式轉變厚度htr隨β絕對值的增加而增大,但由于升降溫時內應力分布的差異(參考圖12),其效果并不對等.以指數n=2 為例,β=5°C 時的htr是β=1°C 時的2.35 倍,而β=-5°C 時的htr只是β=-1°C 時的2.25 倍.總之,溫差幅值β的絕對值對該問題模式轉變厚度htr的影響顯著.

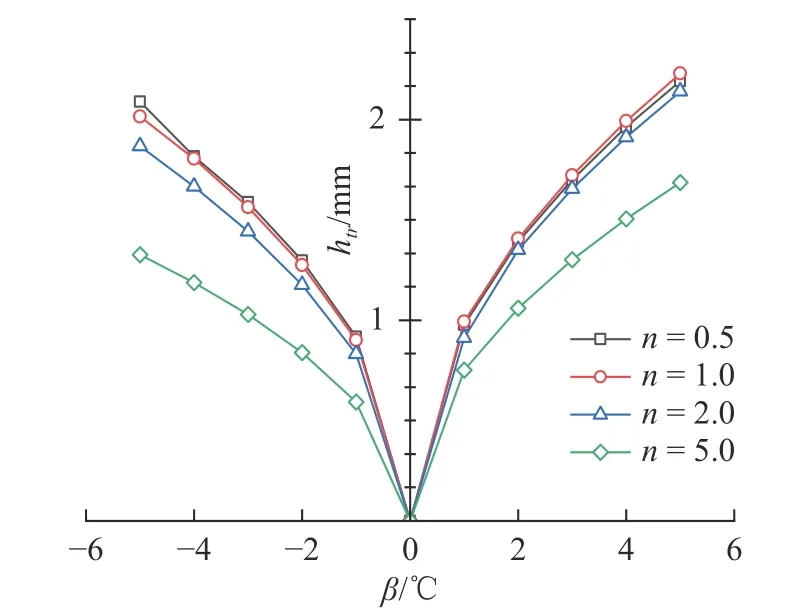
圖13 幅值β對模式轉變厚度 htr 的影響關系Fig.13 Influence of amplitude β onhtr

3.2.2 指數n對htr的影響

給定β=-5°C,-3°C,3°C和5°C,在[0.5,5]間每隔0.5 共取10 組非零n值進行計算,圖14 所示為給定β時 圓形板狀結構的模式轉變厚度htr隨n的變化關系.

圖14 指數 n 對模式轉變厚度 htr 的影響關系Fig.14 Influence of index number n onhtr

由圖14可以看出,溫差幅值β正負的不同,模式轉變厚度htr隨n的變化規律明顯不同.對于同等溫度幅值,升溫時結構更容易發生屈曲失穩.溫差幅值β為正時,模式轉變厚度htr隨n先略微增大后又略微減小,n=1 時htr為最大;溫差幅值β為負時,模式轉變厚度htr隨n單調減小;但總體影響幅度并不十分顯著1進一步計算表明,指數h 對屈曲波數具有顯著影響..例如,對于β=3°C 的情形,n=5 時的htr比n=0.5 時減小了23.38%;對于β=-3°C,n=5 時的htr比n=0.5 時減小了35.29%.總之,與幅值β的影響相比,指數n對模式轉變厚度htr的影響相對較小.

本節所研究問題中轉變厚度htr的變化規律表明,板狀結構因內部不協調變形誘發的屈曲失穩是一個復雜的自發大變形過程,與產生內部不協調變形的各個因素密切相關.

4 結論

本文在板狀結構中引入沿厚度不變的不協調初始應變,通過三維大變形有限元分析,將結構的變形能分離為類伸縮能和剩余能,提出板狀結構屈曲失穩的能量條件,建立了板狀結構自發大變形問題的研究方法,從三維大變形角度,揭示了板狀結構屈曲失穩的物理機制.根據本文工作,可得到以下結論.

(1)在板狀結構大變形過程中,當剩余能從零增加到與類伸縮能相等時,板狀結構將發生由面內伸縮模式為主導到離面彎曲模式為主導的屈曲失穩,經典的載荷屈曲條件是本文能量屈曲條件在外力作用下的特殊情形.

(2)對于受外力作用的板狀結構,由于結構內部壓應力場分布和變化相對簡單,大變形時剩余能將從零快速增加至超越類伸縮能,使得結構發生驟然屈曲失穩現象.

(3)在內部不協調變形因素作用下,由于板狀結構內部壓應力分布的不均勻性、甚至拉應力的存在等多種原因,大變形時剩余能經歷一個從小到大量變、再到超越類伸縮能質變的逐步變化過程,因而,結構一般不會發生驟然的屈曲失穩.

(4)不協調因素是板狀結構在無外部約束下仍存在復雜內部應力分布的主要原因,所誘發的自發大變形(包括屈曲失穩、后屈曲等)是樹葉、花朵等板狀生物結構形成豐富形貌的物理機制.

本文借助三維有限元方法,數值分析了板狀結構在多種因素作用下的大變形過程,重點考察了該類結構的屈曲失穩行為,揭示了不協調因素對轉變厚度的影響規律.實際上,基于本文的三維大變形有限元方法,還可進一步研究板狀結構在不協調因素作用下的后屈曲行為及復雜結構形貌,這些內容的特點是運用微分幾何的曲面論知識分析板狀結構中面在經歷自發大變形后的形貌特征,是本文作者正在開展的工作.

附錄

對于前后兩邊自由、左右兩邊簡支、左端沿x方向施加沿厚度均勻分布壓縮載荷q的正方形板狀結構,薄板理論給出的屈曲載荷計算公式為[32]

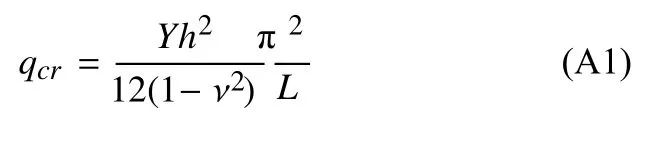
式中,qcr為屈曲載荷,L為正方形板的邊長.

對于圖3 所示的問題,L=600 mm,Y=2.55 GPa,v=0,屈曲載荷值qcr隨厚度h的變化如圖A1 所示.特別地,經式(A1) 計算,qcr=228 N/mm 對應的厚度為h=8.076 mm.