基于時程深度學習的流場特征分析方法1)

戰慶亮 白春錦 葛耀君

* (大連海事大學交通運輸工程學院,遼寧大連 116026)

? (同濟大學土木工程防災國家重點實驗室,上海 200092)

引言

流動特征的識別是一類復雜的數學物理問題,是流體力學研究中亟待解決的難點[1].非定常流場降階模型(reduced-order model,ROM)是一種重要的研究方法,能夠對實驗或計算樣本數據建立提取模型,實現系統辨識[2]及流場的特征提取[3]等.

傳統的流場降階模型研究對象,均針對實驗或計算的快照(snapshot)開展研究,建立一系列不同時刻的樣本數據集,進行流場特征的分離與提取.然而這類方法在數據采集、特征提取和分析等方面存在著諸多困難,尤其是實驗中流場快照的獲取極為困難.例如在風洞和水洞試驗中,為了確定流場的形態需要采用顯示技術進行流場顯示,如煙流法[4]、氫氣泡法[5]等,雖然通過觀察能夠得到剪切層和卡門渦等流動現象[6],但是無法獲取定量的流場數據.再如激光多普勒測速儀(laser doppler anemometer,LDA)[7]、PIV[8]等方法利用示蹤粒子的散射特性計算流場的速度分布,然而粒子類方法大多針對流場中固定切面進行,容積內全場三維測量仍難實現.

隨著計算機和大數據方法的發展,深度學習在流體力學問題的研究中得到了越來越多的應用[9-10],如計算網格的生成[11]、基于神經網絡模型的雷諾應力模型[12-13]、渦激振動的流動控制[14]、尾流狀態的流動控制[15]、高精度流場預測方法[16]、流場狀態的自動識別[17]等.同時,深度學習也為流場特征識別提供了新的思路.如Murata 等[18]用深度學習方法對瞬態流場進行模態分解,得到了比傳統模態分解精度更高的結果.Omata和Shirayama[19]提出了基于自編碼模型的瞬態流固耦合分析方法,同樣采用數據驅動的方案得到了流場的低維表示.Fukami 等[20]提出了基于卷積神經網絡的自動編碼器,進行流場的非線性自動編碼模式提取特征,同時保持不同特征的能量關系.

上述的流場特征識別研究都基于瞬態的全場流場快照開展,對多個時間序列的瞬態數據進行處理,從矩陣理論出發得到流場的模態特征.這些方法所采用的數據有著共同的不足:其空間維度的分辨率遠遠高于時間維度的分辨率.這些方法在處理復雜湍流等問題仍有很多不足[21-22],很大一部分原因是其難以實現更高時間分辨率的數據處理,而這恰恰是復雜湍流特征研究中的關鍵.

針對上述難點和問題,本文提出了流場特征識別的新方法:基于一點處流場物理量的時程為特征提取對象,采用基于卷積自編碼方法的深度學習模型進行時程數據的抽象特征提取,獲得降維后的原始時程的表征編碼,對編碼進行聚類分析從而得到具有不同特征狀態的流場分布規律,實現流場特征分析.并利用本方法進行了低雷諾數圓柱繞流流場特征的自動分類,進行基于一點時程信息的流動狀態的特征分析.

1 流場特征深度學習分析方法

流場中不同位置處的流動特征既相關又不同,傳統特征工程等研究方法難以從復雜系統中識別并區分其中的關鍵流動特征.本文方法的整體流程如圖1 所示,通過基于流場時程自動編碼(flow time history auto encoder,FTH-AE)的方法對流場系統進行特征提取與降維,以流場中不同位置處測點的時程作為研究對象,提取出不同位置處時程關鍵特征的低維表征[23],并實現基于不同特征的流場區域識別與分類.

圖1 流場特征分析方法Fig.1 Methodology of flow feature analysis

FTH-AE 模型的具體實現原理如圖2 所示,模型包含輸入層、卷積編碼層、特征代碼層、卷積解碼層、輸出層和分類器共6 部分組成.輸入層輸入流場中不同位置處的時程數據x,通過編碼器進行特征提取與壓縮,得到低維空間中的特征代碼λ;特征代碼通過卷積解碼器對代碼進行還原,使得輸出與輸入的時程信號x′相同.

圖2 流場特征分析方法及FTH-AE 模型結構示意圖Fig.2 Structure of FTH-AE model

根據FTH-AE 模型的計算原理,在訓練過程中是無監督的訓練方式,即不需要輸入流場樣本所屬類型或者特征,因此適用于任意復雜的流動問題.進而時程分類器對低維空間中的特征代碼進行聚類(K-Means)運算,得到低維空間中樣本的分類標簽,完成輸入流場時程的特征分類.

為保證時程特征分類的準確性,FTH-AE 模型設計中要滿足以下條件(1)根據流場及其樣本特征,選擇合適的卷積編碼器結構(2) 為保證特征代碼λ能夠準確表征輸入x的特征,編碼器與解碼器需滿足下式的變換

其中Fe表示編碼部分,Fd表示解碼部分,x為輸入的流場時程數據,λ為流場時程的特征編碼.由FTHAE 模型結構可知,其輸入與輸出數據類型是相同的,模型無監督學習的目標是使得輸入與輸出盡量保持相同.如果模型在訓練后滿足式(1),那么模型的編碼層與解碼層中就自動提取得到了訓練數據的關鍵特征,也即整個流場域內流場樣本的特征,并將這些特征對應到了模型的特征代碼空間中,可以針對降維后的模型編碼進行進一步的特征分類計算.卷積層中對輸入數據的計算過程為

其中T為輸入數據的長度,l為卷積核的大小,K為當前層的卷積通道個數.在計算過程中,各通道采用了“共用權值參數w”的方法,減少了模型參數個數,同時共享了偏置矩陣bn.

為保證輸入數據的特征的準確表征,模型中采用全卷積形式進行數據的壓縮與還原.如果模型已成功訓練到輸出數據與輸入數據近似相等,表明高維數據已成功映射到低維特征向量λ中.

2 流場時程數據提取

本文以低雷諾數圓柱繞流場為例驗證方法的可行性與準確性,數據采用數值模擬方法[24]獲取,計算域如圖3 所示,雷諾數ReD=200.圓柱的直徑D=1,圓心為坐標原點.計算域順流長度為44D,上、下游長度均為22D;橫向長48D,上下均為24D.圓柱周圍矩形區域內使用較密集的非結構化三角形網格,距離圓柱較遠的區域的網格劃分比較稀疏.左側入口邊界為速度入口,右側出口處的邊界為壓力出口,其余為對稱邊界.

圖3 整體及局部的網格劃分Fig.3 Global and local meshes

在圓柱繞流模擬中,圓柱壁面附近及尾流區域的流場受到干擾,流場特征豐富,適于選做研究對象.在圓柱周圍選取了7122 個測點隨機均勻分布在網格密集的矩形區域內,捕獲該范圍內流場的時程數據,測點分布如圖4.

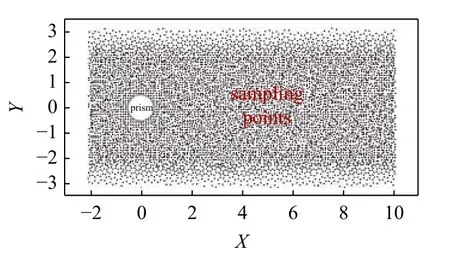
圖4 測點位置示意圖Fig.4 Location of sampling points

考慮到所選測點較多覆蓋范圍較大,樣本所包含的特征各不相同.為了直觀展示樣本集中數據特征的多樣性與復雜性,在圓柱周圍的流場中隨機選取6 條流向速度時程曲線進行展示,如圖5 所示.圖中時程曲線的振幅、頻譜分布等特征均不相同,這表明流場中不同位置的時程曲線所包含的流場特征存在差異.

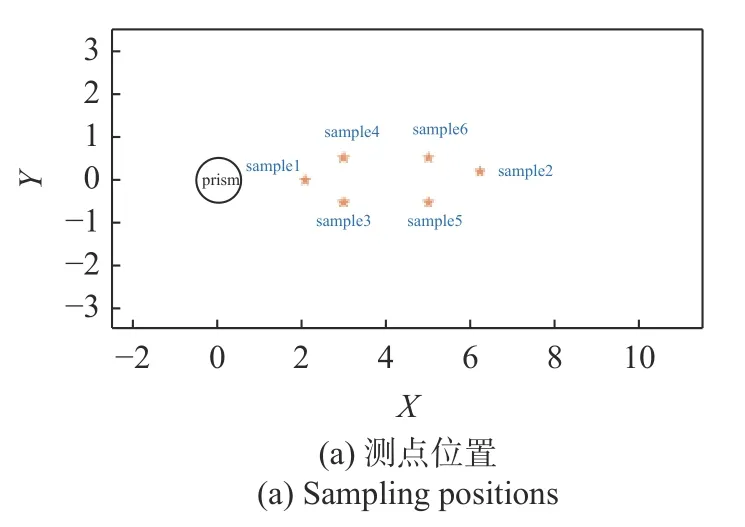
圖5 典型測點的流場流向速度時程Fig.5 Time history of flow field x-velocity at typical measuring points

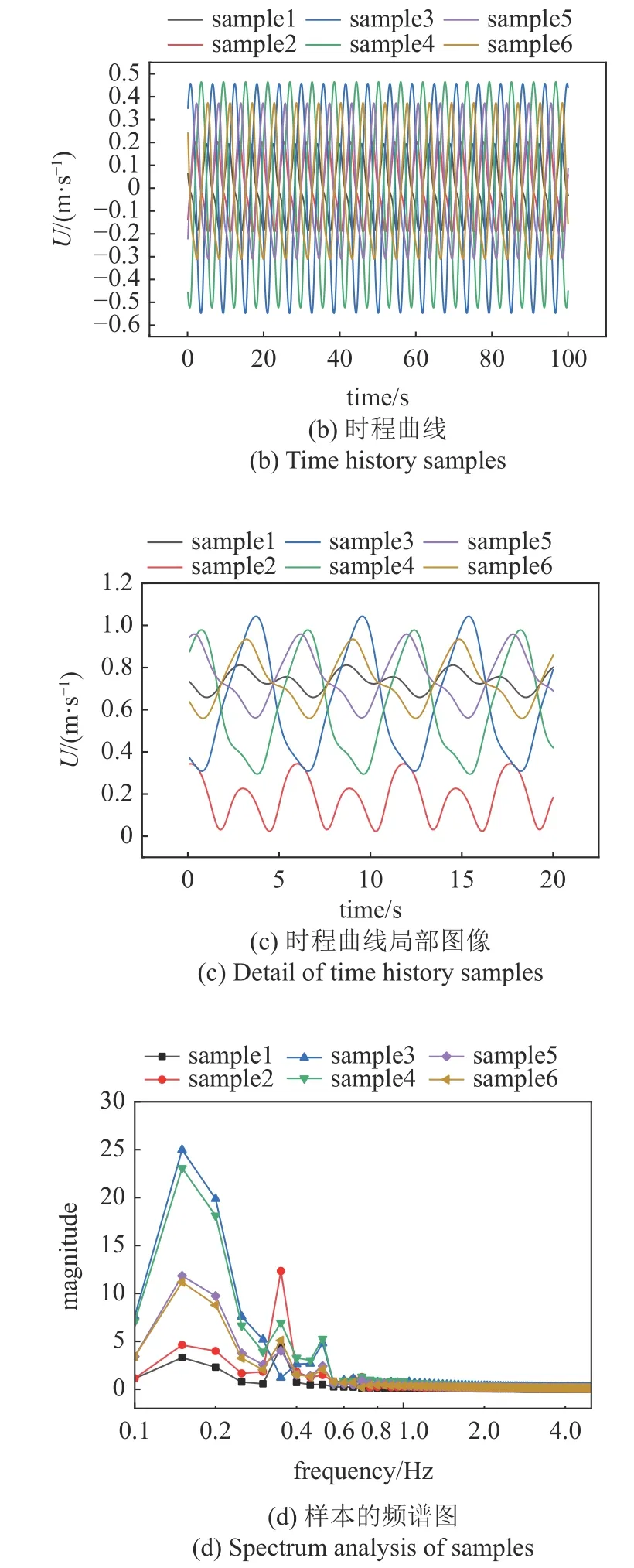
圖5 典型測點的流場流向速度時程(續)Fig.5 Time history of flow field x-velocity at typical measuring points(continued)

3 模型參數及其訓練

為了有效提取流場中不同位置的時序特征,本文的“FTH-AE”模型結合一維卷積進行時程信號的特征提取.其中“Encoder”可以對數據進行壓縮,利用一維卷積在保留數據原始特征的同時對數據進行降維,得到原始數據的低維度特征.使用“Flatten”層對降維后的數據進行拼接,再通過“Dense”層將數據輸出為所需的維度.“Decoder”可以根據壓縮后的低維度特征將數據還原成原始數據,其輸入為“Encoder”的輸出再使用一維反卷積層實現數據的解碼還原.具體參數如表1 所示,其中“Conv”表示卷積層,Conv_T 表示反卷積層,激活函數采用ReLU 函數表示自動編碼特征分類模型參數.

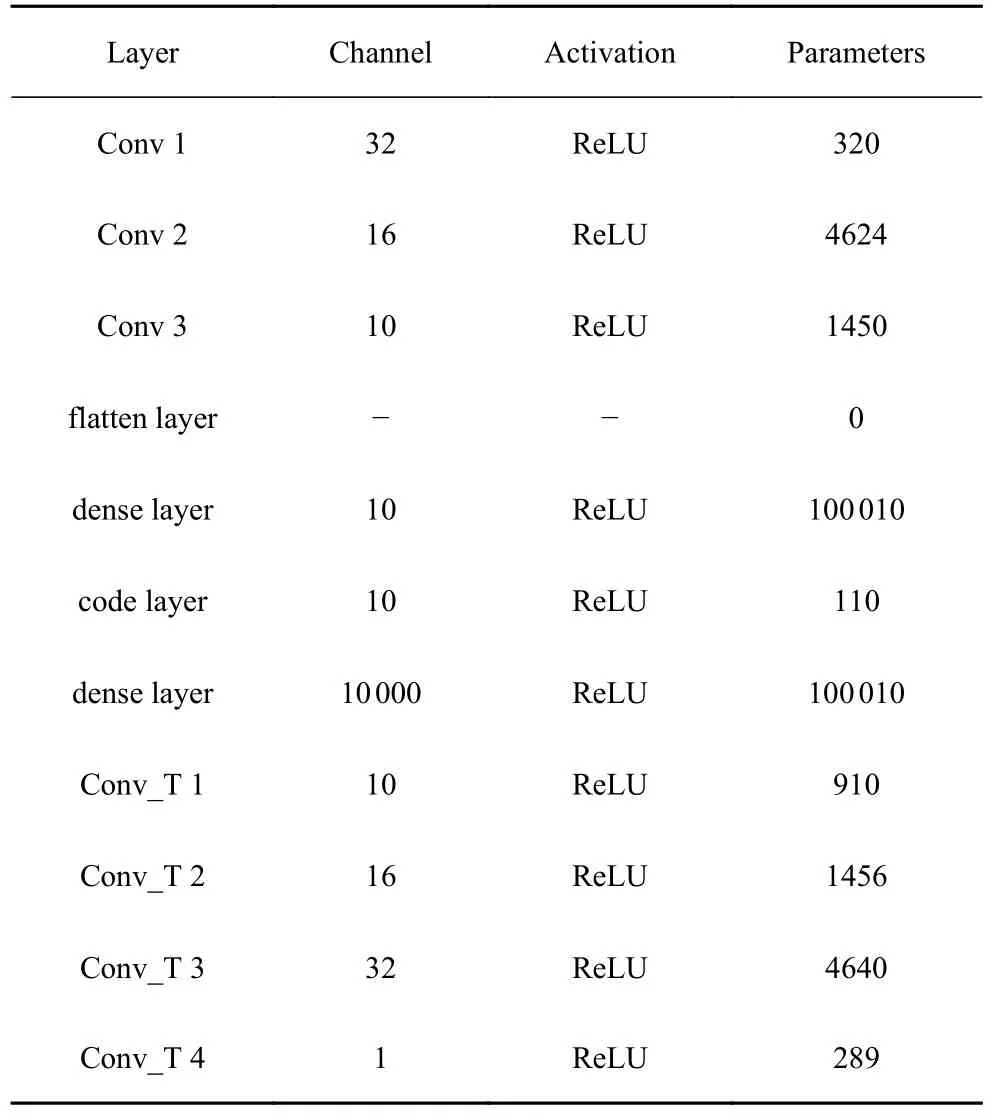
表1 FTH-AE 模型參數Table 1 FTH-AE model parameters

模型中所有卷積核的尺寸均為9 的偏大尺寸的卷積核,獲得較大范圍的局部時程信息,有利于模型的收斂.卷積層的卷積核個數分別為32,16 與10,經過系列卷積變換的輸出尺寸為1000 × 10,為了保留卷積權重與時程序列之間的對應關系,本文使用“Flatten”層附加10 層全連接層進行降維,最終將單個時程樣本壓縮為10 維空間中的一點.模型的解碼部分各參數與編碼部分相對應,順序相反.

本模型訓練采用的是無監督訓練模式,數據集中沒有指定的標簽,且所有數據都為訓練集.采用ADAM 方法加速模型收斂,參數選為1.0×10-4.訓練的批量大小(Batch_size)為8,輸入與輸出之間的差異用MSE 損失函數(loss)來衡量,訓練次數設置為500 次.同時設置“Earlystopping”為40,即在訓練過程中若損失值在40 步內無下降則網絡自動停止訓練.經過計算得到了迭代過程中損失函數曲線如圖6所示,模型的最終損失值為1.0×10-4.

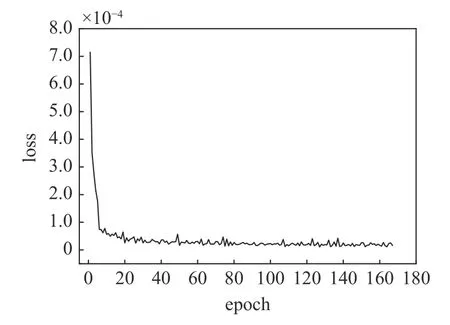
圖6 自動編碼特征分類網絡損失值Fig.6 Loss of FTH-AE with respect to epoches

4 結果與分析

4.1 特征編碼的準確性驗證

自編碼模型結構為無監督學習模型沒有測試集,殘差值即為輸入數據被模型編碼與解碼前后的差異,損失值越小說明網絡對輸入數據特征提取得越精準.為了驗證模型的準確性,選取了6 個測點處順流速度U的原始樣本及深度學習模型的還原曲線進行比較,如圖7 所示.由圖中原始時程與模型結果比較可知,原始數據與根據低維編碼還原的時程曲線差異很小,兩條曲線幾乎重合說明模型可以準確的提取到流場中各個測點處數據的低維度特征.因此,模型的中間的特征編碼層包含了所訓練數據的降維后的特征,且可根據編碼準確還原出原始曲線的特征,因此可利用這些低維空間中的編碼進行原始曲線的特征區分與識別.

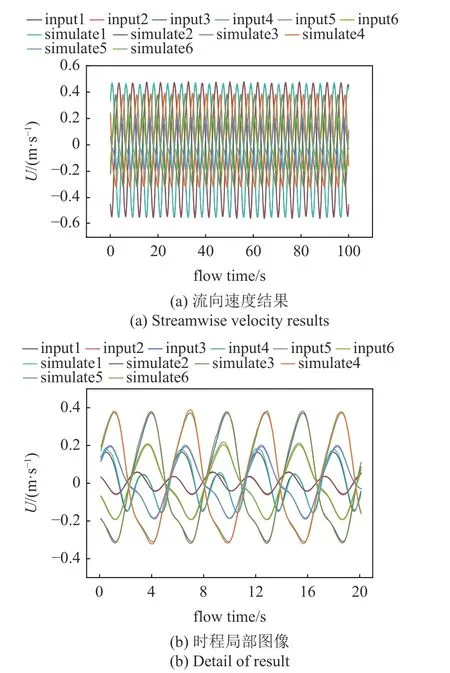
圖7 原始時程與FTH-AE 模擬的時程Fig.7 Original samples and FTH-AE result

4.2 基于降階編碼的流動特征分類

對FTH-AE 模型所得到的低維空間中的編碼特征進行K-Means 計算,即對整個流場的低維表征進行自動分類,可以得到流場中不同特征時程的分類結果,進一步將分類結果按照流場測點的位置進行顯示,所得結果如圖8 所示.其中圖8(a)表示不考慮流場均值的特征分類結果,可見根據深度學習模型所提取的測點的特征,可以將整個流場分為3 類區域:綠色區域、藍色區域和橙色區域.圖8(b)為對應的不考慮流場均值的模態分解結果,比較兩圖可以發現深度學習模型成功得到了流場的主要模態,即流場的最重要的“特征”.不同的是,DMD 方法基于矩陣理論進行了特征提取與分解,而本文則直接根據流動特征進行了自動的特征提取與識別.

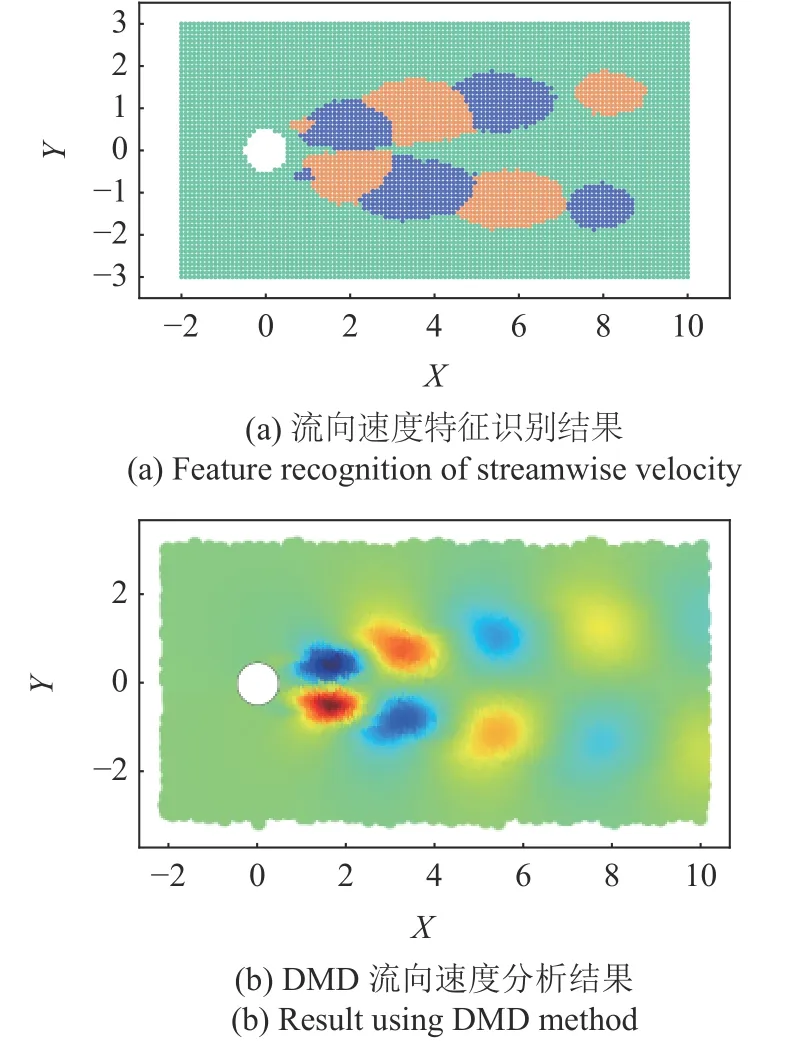
圖8 尾流特征識別結果Fig.8 Feature recognition of wake

為了明確流場特征分類的物理意義,闡述“深度學習究竟學習到了流場的哪種特征”,進一步對不同分類區域內的流場測點處時程進行了舉例分析,結果列于圖9.

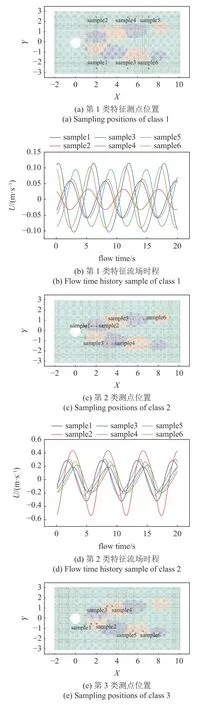
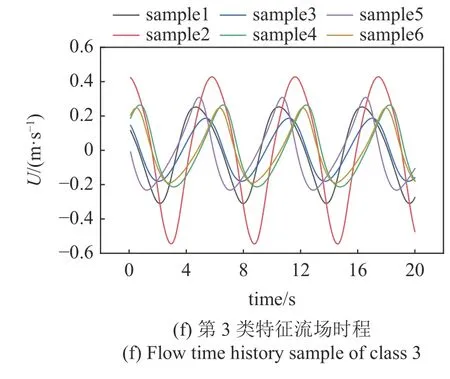
圖9 不同類型的時程特征分析Fig.9 Feature analysis of different class

為方便結果分析,定義綠色區域內的流場時程為第1 類特征,藍色區域內的流場時程為第2 類特征,橙色區域內為第3 類特征.分別在3 類特征的測點中選擇6 個測點,測點位置見圖9(a),圖9(c)和圖9(e),對應位置處的順流速度時程見圖9(b),圖9(d)和圖9(f).通過觀察,可以發現3 類時程的明顯特征差異:第1 類特征的曲線振幅都偏小,這些測點位于渦脫區域外部;第2 類曲線與第3 類曲線振幅均較大,但是相位相反,即第2 類曲線達到極大值的時刻對應的第3 類曲線均位于極小值,這些測點均位于尾流中的對稱渦脫區.由于本算例所研究的流場簡單,因此對應特征容易通過人為觀察發現其中的規律,同時也可驗證本文的模型自動識別結果是準確的.

5 結論

本文提出了基于時程數據的自編碼流場特征識別方法,通過對流場時程進行特征提取,得到復雜流動數據的低維表征,并對低維編碼聚類分析獲得不同特征的流場分布.作為研究算例,對低雷諾數圓柱繞流流場進行了驗證,結果表明模型能夠準確還原空間不同位置處的時程曲線,驗證了模型的準確性.進一步,對低維的模型編碼進行了聚類分析,得到具有不同特征的流場區域分布,與模態分析方法得到了一致的流動特征識別結果,同時對深度學習分類的結果進行了物理解釋.本方法從流動的時程特征角度實現了流動特征識別,是一種全新的流場分析方法.雖本文研究的計算算例流場特征相對較簡單,但本方法同樣適用于復雜流場特征的自動識別研究,借助深度學習強大的特征提取能力,可實現復雜流場的深度特征分析.