平穩/非平穩激勵下中厚圓柱殼隨機振動響應的基準解1)

霍慧 陳國海 王文培 楊迪雄

(大連理工大學工業裝備結構分析國家重點實驗室,遼寧大連 116024)

引言

作為工程實際中常見的結構形式,圓柱殼得益于其優良的結構特性和力學性能,被廣泛應用于潛艇、火箭、導彈、飛機、儲液罐等工程結構中[1-5].其中,考慮橫向剪切變形和轉動慣量影響的中厚圓柱殼結構不可避免地會承受各類隨機激勵作用,如隨機地震動、風載、噪聲激勵等[6-7].因此,中厚殼隨機振動分析和不確定性傳播研究對其設計和安全服役具有重要的理論意義及應用價值.

自Love 建立殼體基本方程以來,已有許多學者和工程師對中厚圓柱殼結構的自由振動特性進行了分析[8-9].Leissa[10]對殼體自由振動理論進行了深入廣泛的論述.然而,目前僅有簡支邊圓柱殼能獲得精確解析的自振頻率和振型函數.為此,各種數值解法被相繼提出,如動力剛度法[11]、傅里葉級數法[12]、有限元法[13-14]、波函數法[15]等.

實際工程中,殼體結構經常承受環境動載荷作用.最近幾年,確定性動載荷作用下圓柱殼的動力響應研究已經得到了廣泛關注,載荷形式包括黏性流體[16]、移動載荷[17]、溫度或濕度場[18]、磁場作用[19]等.由于服役環境的復雜性,動力載荷普遍具有隨機性,通常采用隨機過程對其進行表征.基于狀態協方差分配法,To和Chen[20]給出了非平穩隨機激勵作用下壓電殼體元件的最優隨機振動控制方案.針對邊界隨機激勵作用下的壓電空心圓柱厚殼,Ying等[21]基于伽遼金法計算了隨機響應的統計矩.Esmailzadeh和Lakis[22]采用有限元方法求解了湍流邊界層激勵作用下的開口薄殼振動響應.基于FPK (Fokker-Planck-Kolmogorov)方程,Asnafi[23]獲得了隨機激勵作用下圓柱淺殼的概率密度函數.Li 等[24]利用辛對偶方法研究了層合圓柱殼在軸向壓縮和湍流邊界層激勵下的隨機振動響應.

此外,Crandall和Elishkoff[25]以圓柱殼為研究對象,揭示了振型互相關項對隨機振動響應具有不可忽視的作用.振型互相關項的重要作用也在球殼[26]、多跨梁[27]中被深入考察.對于離散多自由度系統,林家浩等[28]提出了高效的虛擬激勵法,該方法精確計入振型互相關項.Chen 等[29]將虛擬激勵法推廣到連續體,獲得了薄殼平穩隨機振動響應的解析精確解.相比于薄殼,中厚殼在實際工程中的應用更加廣泛,還會受到非平穩隨機激勵作用.因此,本文針對中厚圓柱殼,開展平穩、非平穩隨機振動分析,以獲得其隨機響應的精確基準解.

為了保證結果的準確性,本文首先通過自由振動分析,獲得了簡支中厚圓柱殼的精確頻率和解析的振型函數.考慮點、線、面隨機激勵,構造平穩和非平穩虛擬激勵,結合振型疊加法,將平穩和非平穩隨機振動分別轉化為簡諧振動和時程分析,推導了中厚圓柱殼隨機響應功率譜的解析表達式.將功率譜在頻域上積分即可得到均方響應及均方根.此外,在解析解的推導過程中還涉及對振型函數空間域積分和時間域的Duhamel 積分.基于符號運算的解析法在中厚殼隨機振動響應解析求解中無法實現多空間點同時輸出,且計算難度和效率隨參振振型的增加而顯著增加.為此,進一步提出了離散解析法.通過對空間域先解析積分后離散,頻域和時域數值積分,將解析運算轉化為矩陣運算,不僅顯著提高了計算效率,而且能批量獲得殼體隨機響應的分布,便于研究參數變化對圓柱殼體隨機響應全局影響.此外,基于精確基準解,深入討論了隨機激勵類型及結構參數對中厚殼振動響應的影響.

1 中厚圓柱殼自由振動精確解

對于殼結構,隨著厚徑比(厚度h與曲率半徑R之比)的增大,剪切變形和轉動慣量對力學行為的影響越來越大,Kirchhoff 薄殼理論不再適用.針對中等厚度圓柱殼(如厚徑比≥1/36～ 1/20),分析應采用考慮橫向剪切變形和轉動慣量影響的中厚殼理論.本文分別討論了如圖1(a)所示的封閉殼(φT=2π)和圖1(b)所示的開口角度φT的開口殼結構.R,L和h分別為殼的半徑、長度和厚度,坐標系(x,θ,z),x,θ,z分別代表軸向、環向和徑向.引入5 個廣義獨立位移描述殼體的中面變形:軸向位移u1、環向位移u2、徑向位移u3、軸向轉角u4及環向轉角u5.考慮橫向剪切變形和轉動慣量的中厚圓柱殼隨機偏微分方程可以描述為[10]

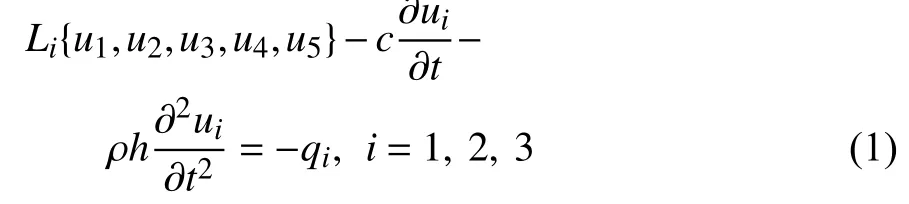
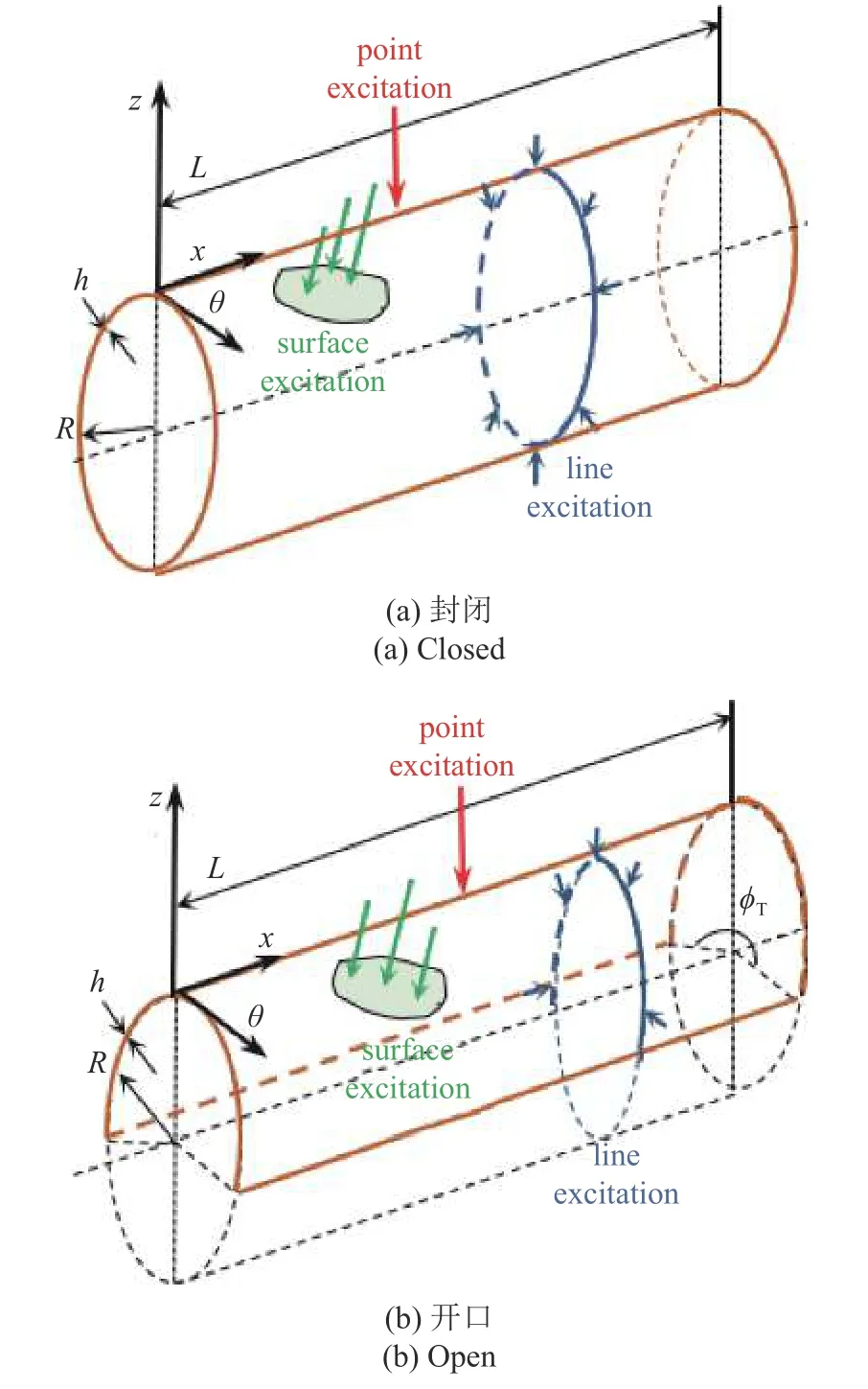
圖1 中厚圓柱殼幾何模型及載荷情況Fig.1 Geometric model and load cases for moderately thick cylindrical shell

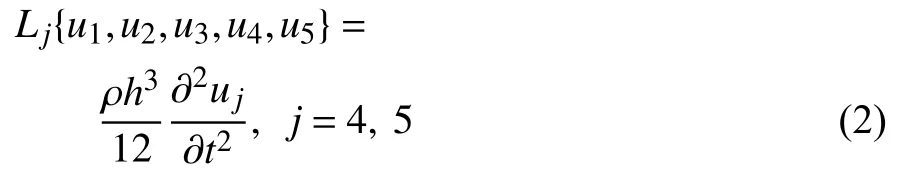
其中c為等效阻尼系數,ρ為體密度,i=1,2,3 分別代表軸向、環向和徑向,j=4,5 分別代表軸向轉角和環向轉角方向,qi為圖1 所示施加在第i個方向上的隨機激勵,L1～L5為微分算子

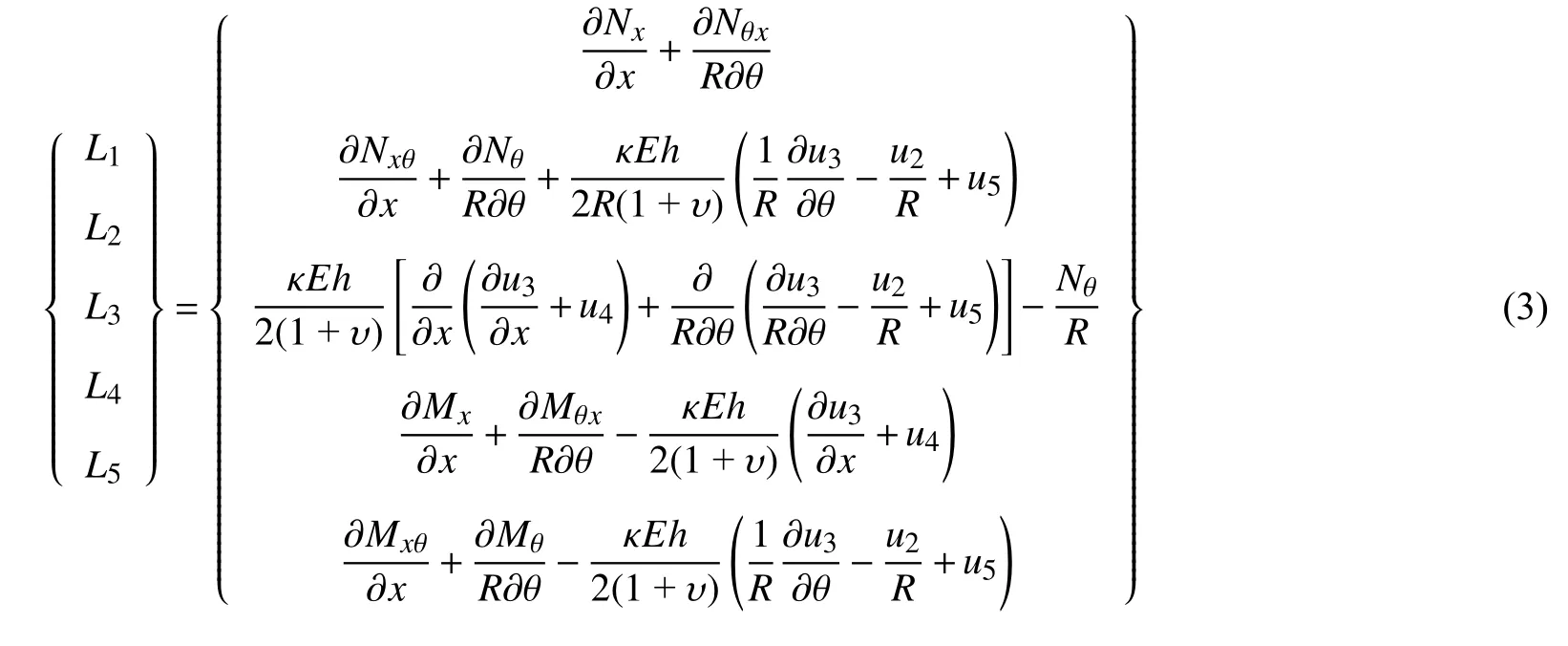
其中,E和υ分別為材料彈性模量和泊松比,κ為剪切修正系數,本文取為5/6[10].薄膜內力Nx,Nθ,Nxθ和Nθx,彎矩Mx和Mθ,扭矩Mxθ和Mθx具體形式分別寫為[30]

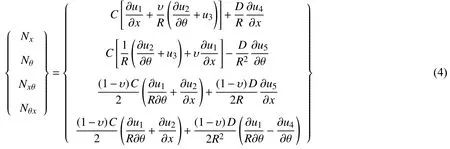
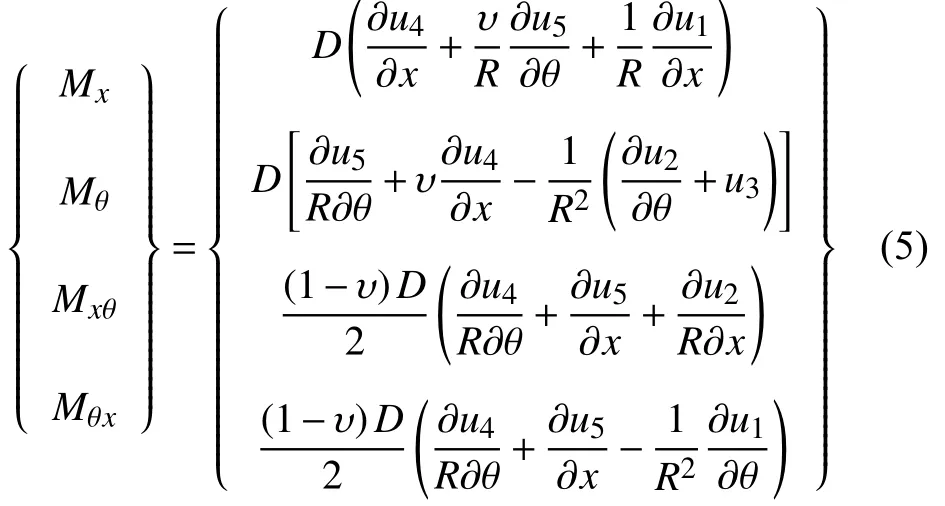
式中,C=Eh/(1-υ2)表示拉伸剛度,D=Eh3/[12(1-υ2)]為彎曲剛度.

為了得到圓柱殼的自振頻率和振型,需進行中厚圓柱殼的自由振動分析.去掉式(1)中的阻尼力項和外力項,即可得到中厚圓柱殼自由振動的微分方程

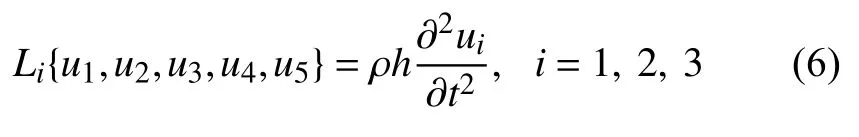
對于如圖1 (a)所示的簡支封閉圓柱殼,其自由振動精確解可設為分離變量形式[10]

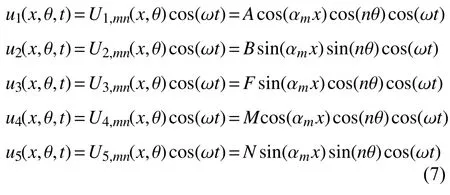
其中,Us,mn(x,θ)為與第s個廣義位移相應的第mn階振型函數,s=1,2,3,4,5 分別代表軸向、環向、徑向、軸向轉角及環向轉角方向,m和n分別為軸向和環向的半波數,αm=mπ/L,A,B,F,M和N為待求常數.將式(7)代入式(6)可以得到

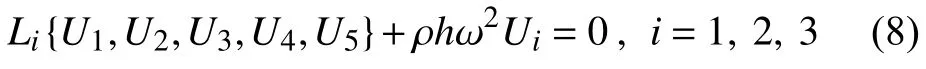
此外,由式(6)和式(7)可以得到矩陣形式的對稱齊次方程組

式(9)中的各個系數分別為

式中,Ω=ωR為待求的無量綱頻率,λ=mπR/L,k=h2/(12R2),Iκ=κ(1-υ)/2.為得到式(9)的非平凡解,令其系數矩陣行列式為0,則可以獲得關于Ω2的五次方的頻率方程

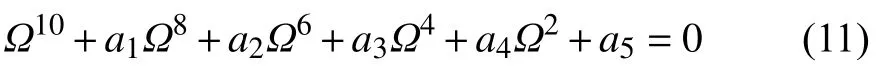
其中,a1-a5為代數方程的系數.求解該方程從而獲得殼結構的精確頻率ω.將求得的自振頻率回代到式(9),就可以最終確定式(7)中振型函數的系數A,B,F,M和N之間的比值關系.

類似地,對于如圖1 (b)所示的四邊簡支的開口形式中厚圓柱殼,其自由振動封閉形式解可以表達為如下形式

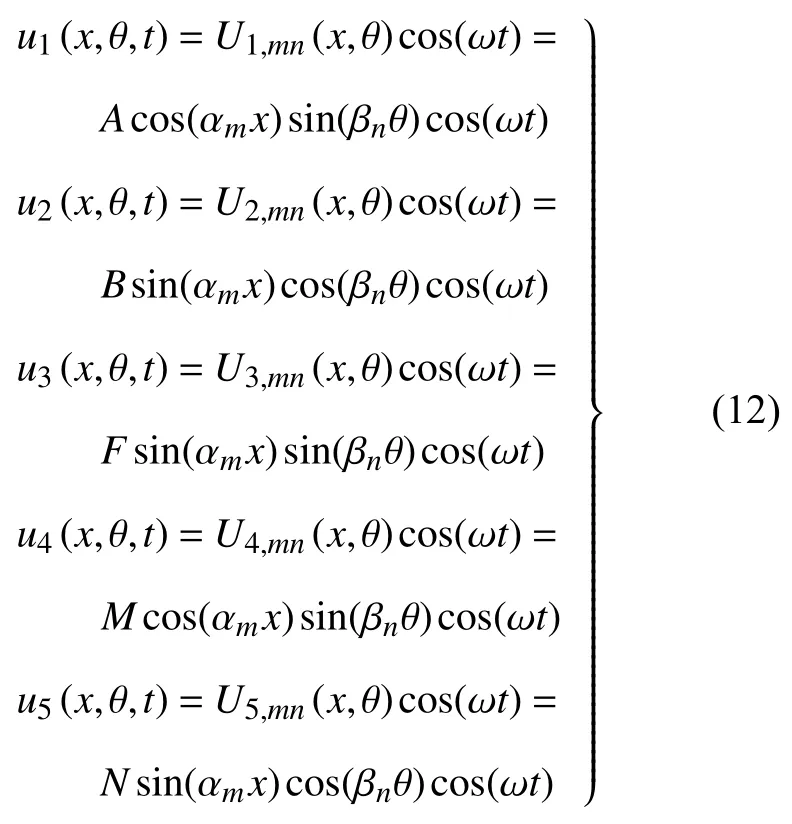
其中βn=nπ/φT.采用與封閉圓柱殼類似的計算步驟,將式(12)代入式(6),得到開口中厚圓柱殼自由振動的頻率方程,同樣可以獲得該結構的精確頻率及解析振型函數.

2 中厚圓柱殼隨機振動響應的解析法

由振型疊加法可知,軸向、環向及徑向上的線彈性中厚圓柱殼位移可以表達為

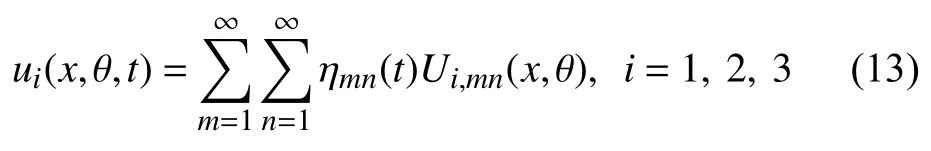
其中ηmn(t)為第mn階振型的正則坐標.將式(13)代入式(1)可以得到

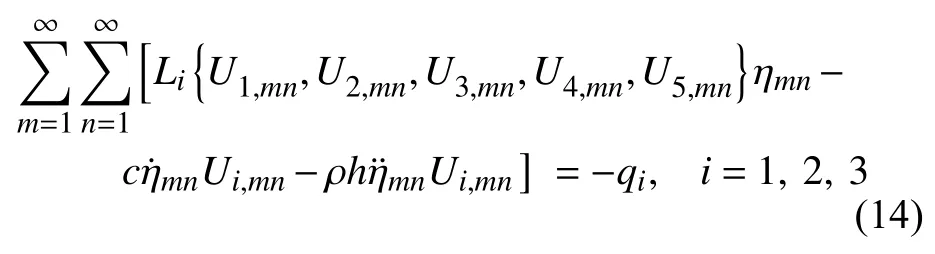
對于i=1,2,3,分別在式(14)兩端乘上第lk階振型Ui,lk,然后將i=1,2,3 的3 個方程在圓柱殼曲面內進行積分,綜合考慮式(8)及振型正交化,最終得到一系列解耦的單自由度系統

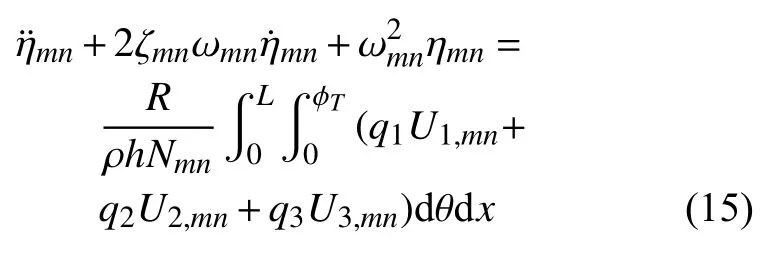
其中 ζmn=c/(2ρhωmn) 為第mn階的中厚殼模態阻尼比,

針對隨機激勵作用下中厚殼的振動分析,基于功率譜的傳統頻域分析方法采用維納-辛欽關系獲得響應的功率譜密度.其中完全二次項組合(CQC)法能夠計及所有參振振型耦合項,但向量乘法運算量過大;而忽略振型耦合項的平方和開平方(SRSS)法計算誤差較大,且僅適用于阻尼比很小、參振頻率稀疏分布的均質系統.因此,本文利用虛擬激勵法和連續體結構解析振型函數,在保證結果準確性的同時只需要計算一次向量乘法,計算效率得到顯著提高.

基于虛擬激勵法[28],構造虛擬激勵

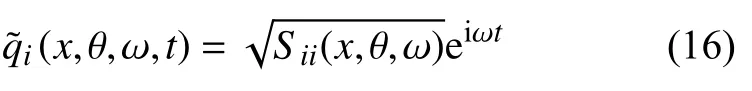
對于平穩隨機激勵qi(x,θ,t)=Γi(x,θ)X(t),其中Γi(x,θ)為作用在第i個方向上的平穩隨機過程X(t)的空間分布函數,式(16)成為

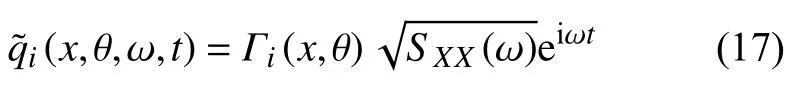
其中SXX(ω) 為X(t)的功率譜密度(PSD)函數.

將虛擬激勵式(17)代入式(15)可以得到

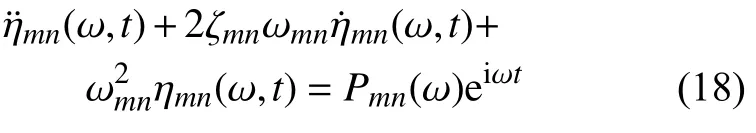
其中

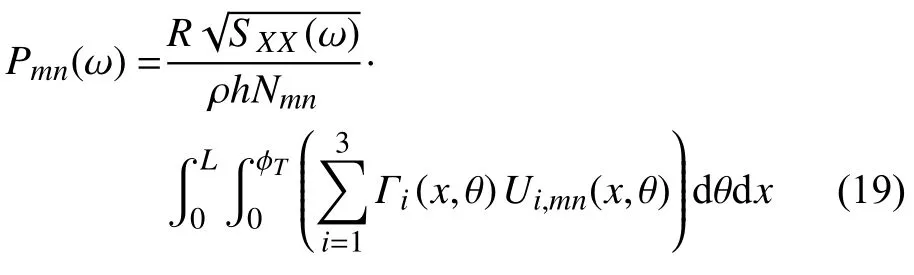
因此,平穩隨機振動分析轉化為確定性的簡諧振動分析,從而得到虛擬正則坐標

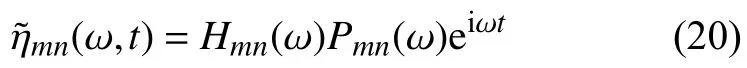
除平穩隨機激勵外,本文還考察統計信息隨時間變化的非平穩隨機激勵.為描述非平穩隨機激勵,Priestley 定義了具有明確物理意義的演變功率譜[31].若平穩隨機過程X(t)表示為:非平穩隨機過程Y(t)可進一步描述為

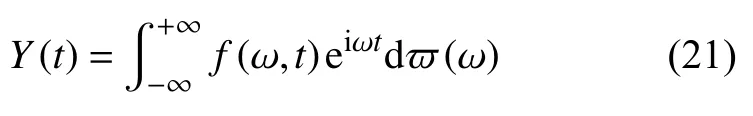
其中,f(ω,t) 為確定性慢變的非均勻調制函數.Y(t)的方差可表達為

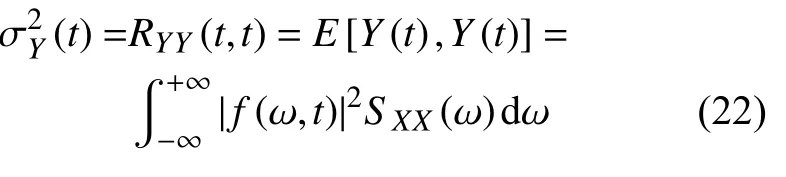
進而得到Y(t)的演變功率譜密度

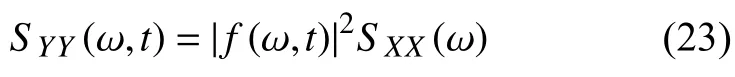
然而,通常難以計算式(23)所示的非平穩激勵下結構隨機振動響應的演變功率譜密度.當激勵功率譜密度函數中的頻率特性不隨時間變化時,將非均勻調制函數f(ω,t)簡化近似為均勻調制函數f(t),此時的均勻調制非平穩隨機過程可以寫為

對于施加在中厚殼第i個方向的均勻調制非平穩激勵qi(x,θ,t)=Γi(x,θ)Y(t)=Γi(x,θ)f(t)X(t),基于虛擬激勵法的非平穩虛擬激勵表示為

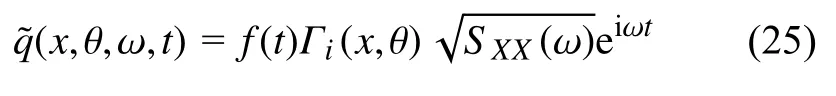
將式(25)描述的非平穩虛擬激勵代入解耦的單自由度系統式(15),可得到

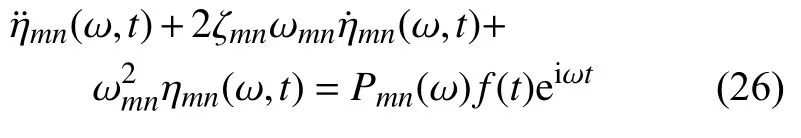
由Duhamel 時域積分,得到虛擬正則坐標

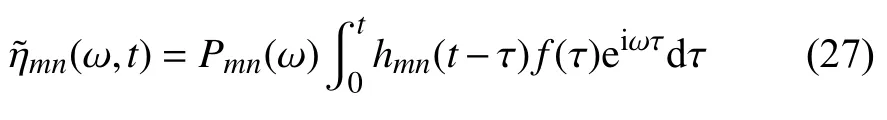
其中hmn(t-τ) 為單位脈沖響應函數,即

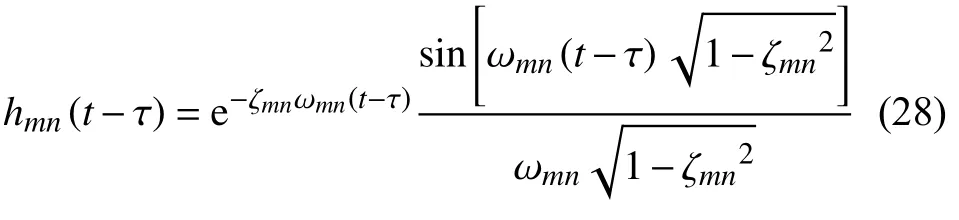
基于平穩及非平穩隨機激勵作用下得到的虛擬正則坐標如式(20)和式(27)所示,進而中厚圓柱殼第i個方向的虛擬位移表示為

進一步,可以基于虛擬激勵法得到各個方向位移、速度及加速度響應功率譜密度函數如下

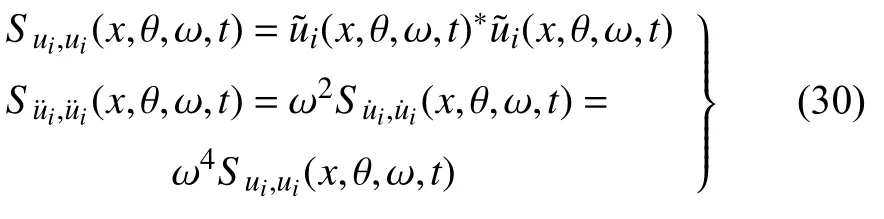
其中,上標“*”表示復共軛.

此外,在虛擬位移響應的基礎上,根據殼結構的幾何關系及材料本構關系,可以由式(4)和式(5)獲得虛擬薄膜內力、彎矩及扭矩

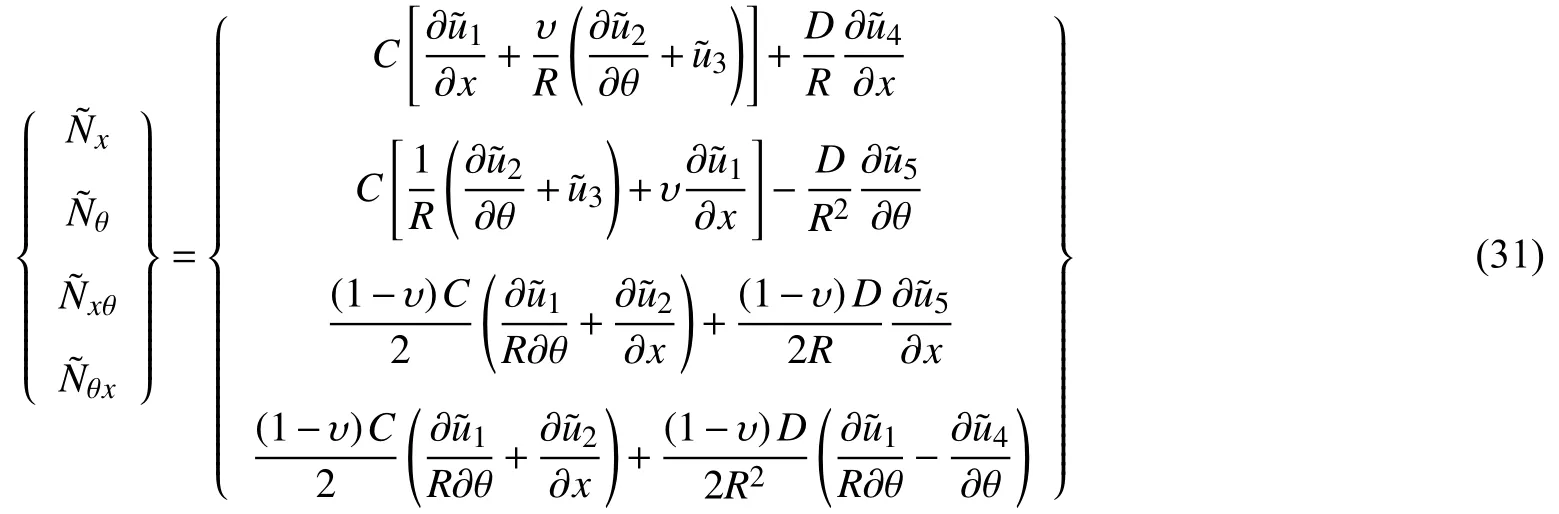
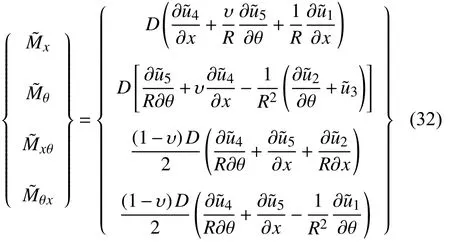
同樣地,基于虛擬激勵法,將虛擬內力響應的復共軛乘上自己本身,可以解析獲得中厚圓柱殼薄膜內力及彎曲內力等待求響應的功率譜密度函數.

此節解析法推導過程沒有引入任何近似,解析地獲得了平穩及非平穩隨機激勵作用下中厚圓柱殼的各類響應功率譜密度函數精確解.

3 中厚圓柱殼隨機振動響應的離散解析法

在上一節的解析推導中,盡管采用了虛擬激勵法,解析解難以滿足求解隨機振動響應多點輸出的需求,且計算難度和效率隨參振振型的增加而增長.為了在保證解析法空間域上精確性的前提下提高計算效率,本節基于空間域解析積分和微分運算后離散化策略,提出了中厚圓柱殼隨機振動響應分析的離散解析法.

針對解析法推導過程中涉及到的振型函數在空間域的積分和微分運算(見式(15)、式(19)、式(31)和式(32)),離散解析法同樣采取了解析求解,即

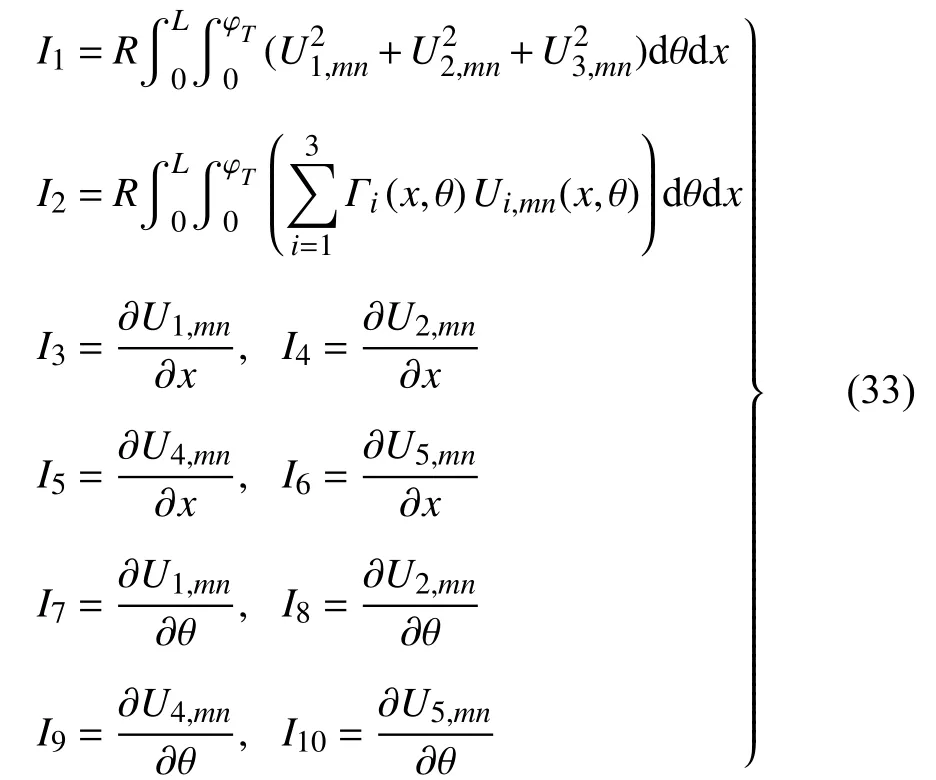
由于引入了圓柱殼的封閉振型函數Ui,mn,如式(7)和式(12)所示,上述積分和微分均可獲得解析解.相比功率譜分析有限元法,采用空間域積分和微分解析運算的離散解析法能保證在空間域的精確性,具有數值方法無法比擬的優勢.

此時,圓柱殼的隨機偏微分方程便轉化為求解式(18)和式(26)所示的常微分方程.在離散化系統中,虛擬激勵法的核心是在響應功率譜密度計算中將向量乘法減少到一次,進而提高計算效率.而在解析的功率譜密度公式(30)中,只涉及符號運算.

為此,將中厚殼結構空間域進行離散,各點位置坐標寫為矩陣形式:r=[r1r2···rNG],rα=(xα,θα)T,α=1,2,···,NG,NG為空間離散點總數,則式(13)描述的中厚殼位移公式可寫為向量形式

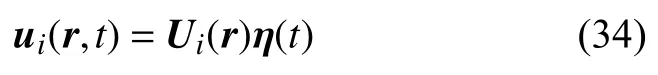
其中Ui(r)為第i個方向上的振型矩陣,矩陣維度為NG×NF,NF表示參振頻率階數,i=1,2,3,η 代表NF維的正則坐標列向量.

作用在中厚殼上的虛擬激勵可以離散化為

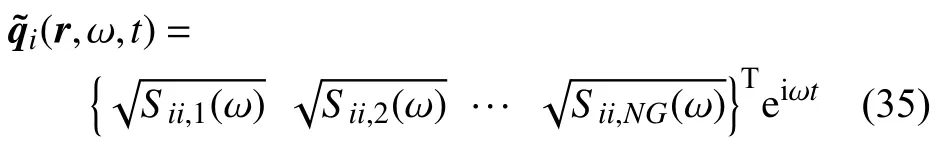
因此,對于平穩隨機振動,第i個方向上中厚殼虛擬位移改寫為向量形式

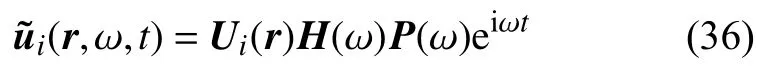
其中,P(ω)為與式(19)對應的廣義激勵的振幅矩陣,H(ω)為頻率響應函數矩陣.由于離散解析法中針對振型函數積分的解析求解(見式(33)中的I1和I2),可知P(ω)在幾何空間域內不涉及離散化操作.將多個節點坐標代入式(36)中振型Ui(r)中,使得離散解析法實現了多空間點虛擬響應的同時輸出,且虛擬位移響應精度與空間離散點多寡無關.

對于非平穩隨機振動,由于Duhamel 積分解析求解通常耗時較長,所以采用高精度的精細積分法取代Duhamel 積分進行時間歷程分析可提高計算效率.將解耦得到的單自由度系統式(26)改寫為狀態空間形式

式(37)求解過程中需要對時域離散化處理,對任意t∈[tk,tk + 1],采用精細積分法對式(37)進行精確高效計算[32],其中tk=kΔt,k=0,1,2,···,Nt,Δt=T/(Nt),T為激勵持續時間,Nt為離散時間點數.從而最終得到中厚圓柱殼在非平穩隨機激勵作用下的虛擬位移響應向量注意到,針對非平穩隨機振動響應分析的離散解析法同樣保證了在空間域的精確性.

基于虛擬激勵法,任一時刻NG個空間點第i個方向的位移響應功率譜密度矩陣為

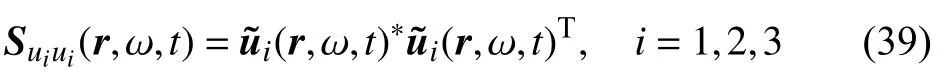
需要說明的是,式(39)需要在一系列離散頻率點ωk上進行計算,其中ωk=ωL+kΔω,Δω=(ωU-ωL)/(Nω),k=0,1,···,Nω,ωU和ωL為截斷頻率上下限,Nω為離散頻率點數.

響應功率譜密度是關于頻率的單變量光滑函數,通過頻率帶寬離散化操作,對響應功率譜密度簡單數值積分即可獲得響應的均方根

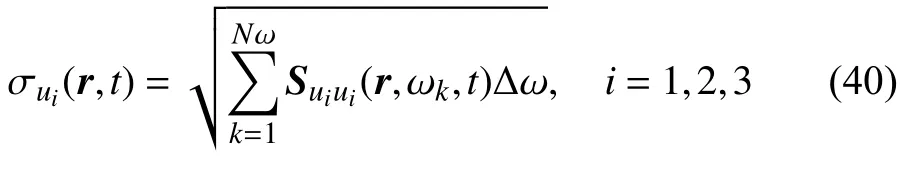
同樣地,基于獲得的虛擬位移響應,亦可容易獲得其他待求響應的功率譜密度矩陣及響應均方根.需要強調的是,在基于有限元計算圓柱殼內力功率譜密度時,內力的計算需要對位移形函數求導,使得連續性減低,導致內力的計算精度比位移低,出現如線性三角形單元中常應力情形.而離散解析法采用位移關于空間坐標的偏導數先解析求導,后將導函數離散化的方式,獲得各類內力分布的精確解,避免了空間離散化對結果精度的影響,所得的內力功率譜和均方根與位移是同等精確的.

因此,本節提出的離散解析法是對解析法的離散化求解,具有極高精度,可作為基準解驗證中厚圓柱殼隨機振動分析的其他數值方法.

4 數值算例

4.1 中厚圓柱殼自由振動精確解

采用文獻[12]中的封閉中厚圓柱殼結構,彈性模量E=210 GPa,密度ρ=7800 kg/m3,長度L=0.502 m,半徑R=0.063 5 m,厚度h=0.003 26 m,泊松比υ=0.28.表1 展示了前5 階精確頻率.文獻[12]及有限元(FEM)所得自振頻率也列于表1.有限元結果基于ABAQUS 軟件,結構模型分別劃分為500,1000,2000,4000,6000 及8000 個S4 R 單元(考慮縮減積分的4 節點彎曲薄殼或厚殼單元) 或S8 R 單元(考慮縮減積分的8 節點雙重彎曲厚殼單元).可見有限元計算精度受限于幾何網格疏密程度和單元類型選擇等因素,存在一定誤差,而文獻級數解[12]與本文所得精確頻率更加接近.

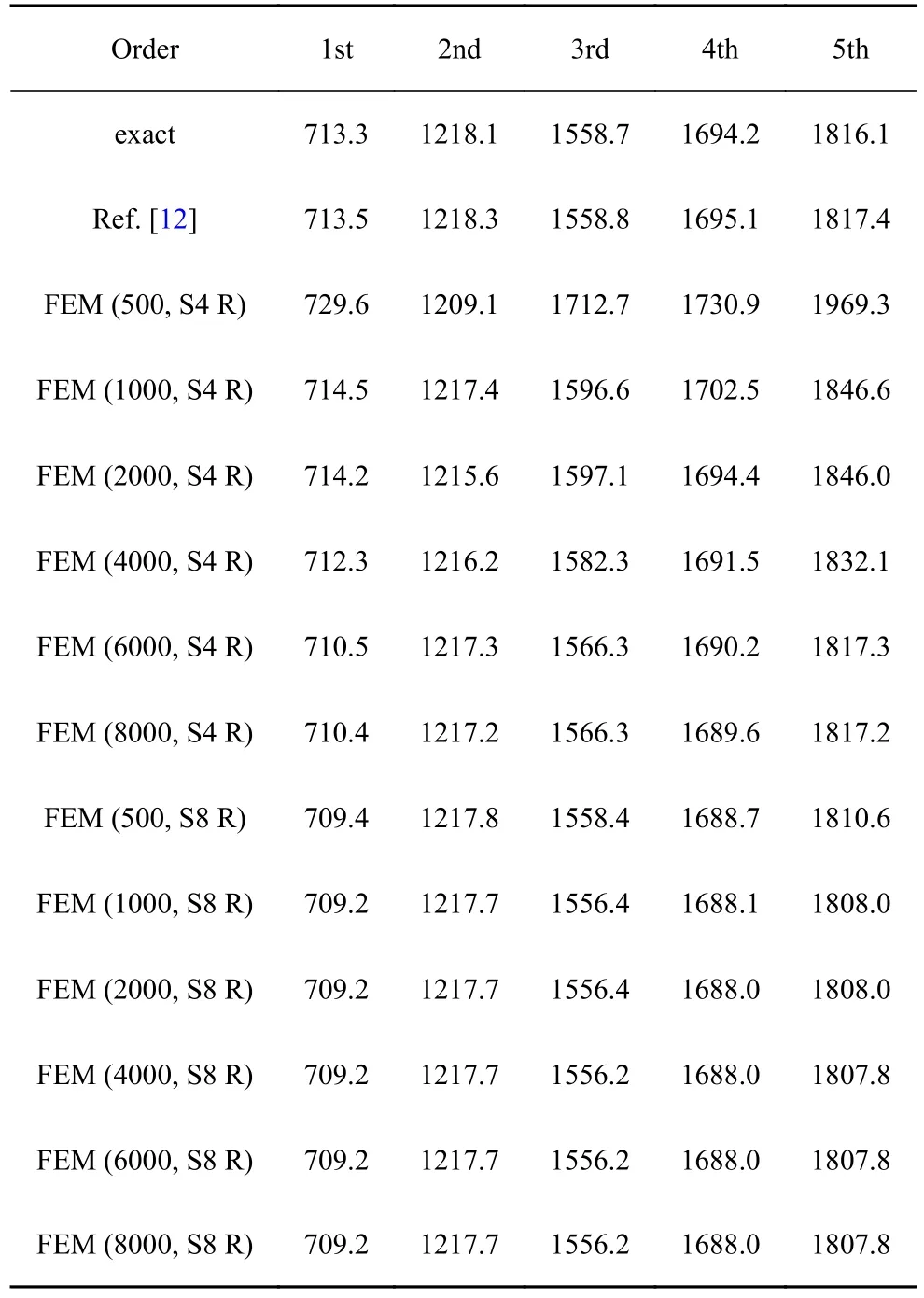
表1 封閉中厚殼的前5 階自振頻率(Hz)Table 1 The first 5 natural frequencies (Hz) of closed moderately thick cylindrical shells

除封閉中厚殼外,考慮一個開口角度為φT=π 的中厚圓柱殼,彈性模量E=27.466 GPa,密度ρ=7850 kg/m3,長度L=14.4 m,半徑R=3.6 m,厚度h=0.36 m,泊松比υ=0.2.圖2 分別給出了開口中厚殼的第1 階、第2 階、第3 階及第5 階自振頻率和振型,有限元結果由ABAQUS 軟件對結構剖分為4000 個S8 R 單元得到.有限元結果與本文精確分析獲得的自由振動自振頻率及振型吻合良好.

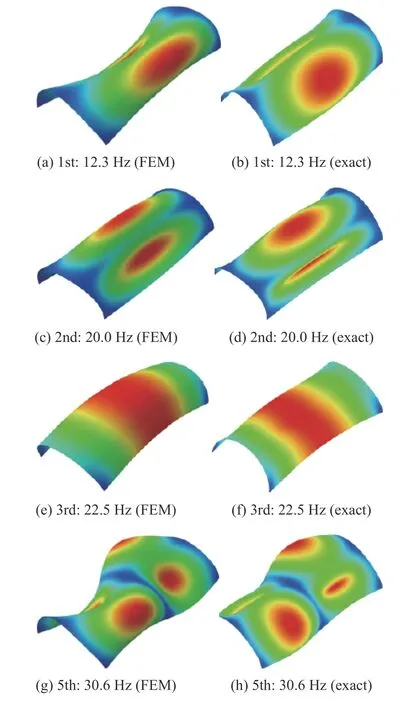
圖2 開口中厚殼的自振頻率(Hz)及振型(精確解和有限元解)Fig.2 Natural frequencies (Hz) and modal functions of open moderately thick shells (exact solutions and FEM results)

4.2 隨機點激勵作用下中厚圓柱殼振動響應

本節考慮如下封閉中厚圓柱殼結構:楊氏模量E=2.96 GPa、密度ρ=0.733 kg/m3、長度L=14.4 m、半徑R=3.6 m、泊松比υ=0.25、厚度h=0.36 m、阻尼比ζ=0.05.分別在兩個空間點 case 1:(L/2,0);case 2:(L/4,π/4)對中厚殼上施加徑向隨機點激勵.該隨機激勵為限帶白噪聲,其頻率范圍為[20,2000] Hz,功率譜密度為1 N2/Hz.

考慮這兩種隨機點激勵,利用解析法(analytical method,AM)、離散解析法(discrete analytical method,DAM)及ABAQUS 軟件計算,表2 分別給出了(L/2,0)處隨機響應的均方根與各方法相應的CPU 運行時間,其中ABAQUS 軟件結果由基于傳統功率譜方法的隨機振動分析模塊給出,中厚殼結構被劃分為4000 (40 × 100)個S8 R 單元.為便于比較計算效率,基于離散解析法的中厚殼結構同樣劃分為4000 (40 × 100) 個網格,空間離散點總數NG為4141 (41 × 101).三類方法均采用激勵帶寬內的全部自振模態參與隨機振動分析.對本小節所考慮的中厚殼結構,頻帶[20,2000] Hz 內存在14 階自振模態,因此式(34)中離散解析法的正則坐標η維度NF取為14.

由表2可知,兩類隨機點激勵作用下,離散解析法所得位移、加速度及彎矩Mx響應及均方根與解析法完全吻合,而ABAQUS 軟件結果與解析法相比存在一定誤差.這驗證了時域、頻域數值積分的精度是非常高的.由于解析法單次只能計算一個空間點響應,為了公平比較三類方法的計算效率,將能夠多點運算的離散解析解及ABAQUS 軟件結果的CPU 運行時間均攤至各節點.可以看到,離散解析解法在保證計算精度的前提下,計算效率得到了極大提升,展示了該方法的計算優越性.值得注意的是,基于空間域離散建模的ABAQUS 軟件結果計算精度依賴于結構的離散形式,而離散解析法基于精確振型函數的解析積分或微分后再將節點坐標代入式(39)中,其空間離散點多寡并不影響離散解析法的計算精度.

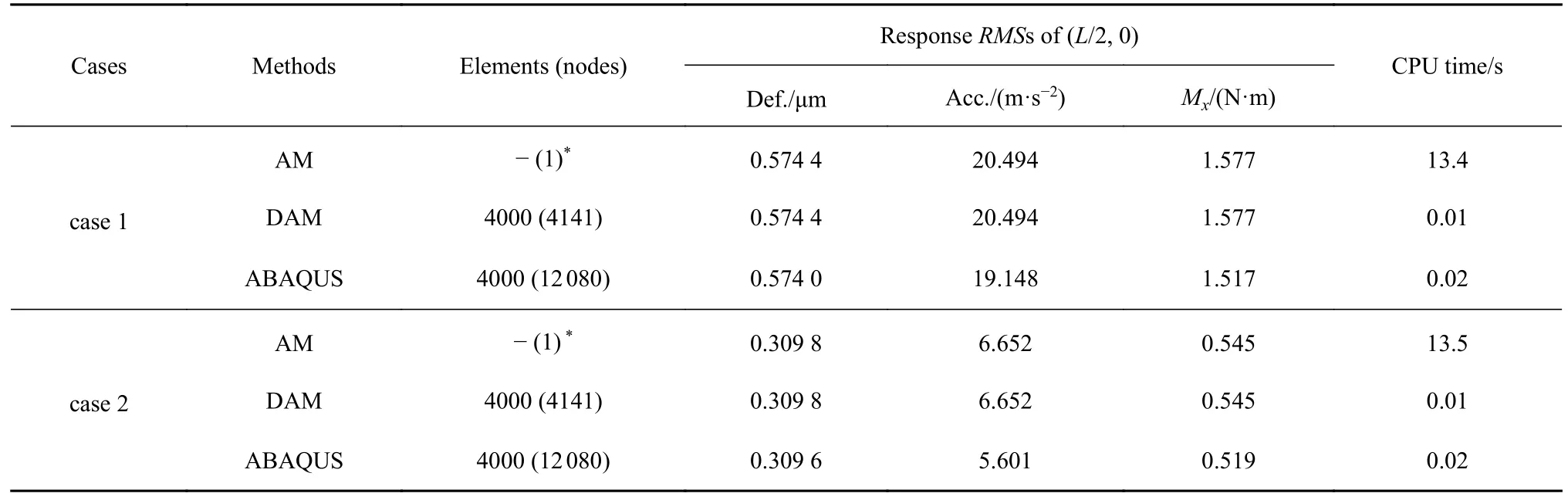
表2 徑向隨機點激勵作用下封閉中厚殼(L/2,0)處響應均方根Table 2 Response RMSs of (L/2,0) for the closed moderately thick shells under random point excitation

圖3 給出了兩類隨機點激勵作用下封閉中厚殼徑向位移響應功率譜密度曲線.除位移外,中厚圓柱殼的內力響應同樣值得關注.隨機點激勵(case 2)下相應的結構薄膜內力Nx和彎矩Mx的響應功率譜在圖4 中給出.結果表明,離散解析法和解析法得到的響應功率譜密度在[20,2000] Hz 內完全吻合,ABAQUS 軟件結果在低頻范圍內與解析解吻合良好,但是隨著激勵頻率增加,ABAQUS 軟件結果呈現了一定的偏差,且ABAQUS 軟件內力計算結果的精度低于位移計算結果.由于解析法結果采用了精確振型,保證了沒有錯根和漏根.因此,這種偏差顯然是由ABAQUS 軟件計算高階自振頻率的誤差引起的.

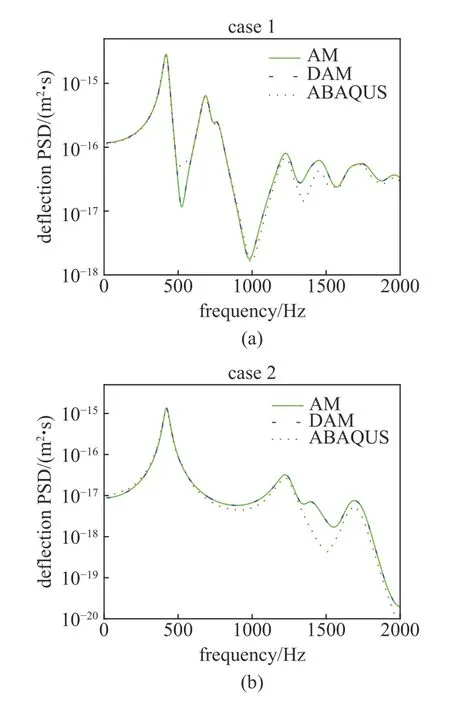
圖3 隨機點激勵下封閉中厚殼(L/2,0)處徑向位移響應功率譜密度曲線Fig.3 Deflection response PSD curves of (L/2,0) for the closed moderately thick shells under random point excitation

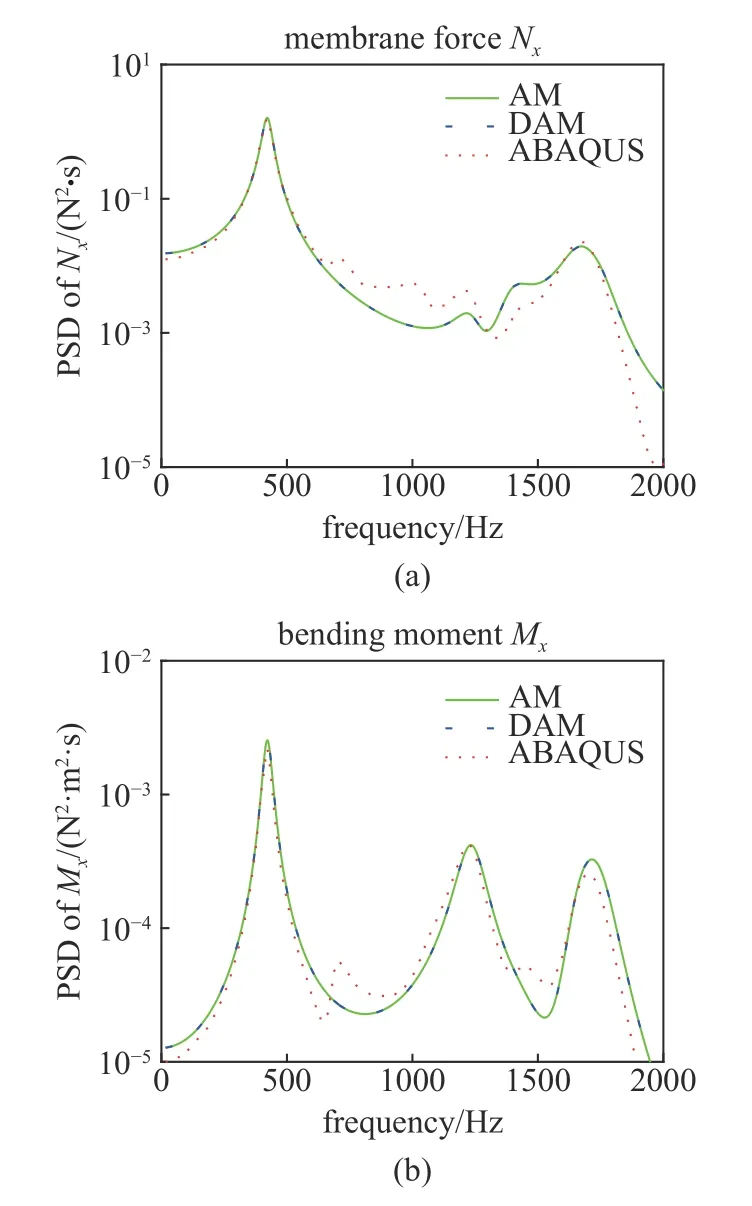
圖4 隨機點激勵(case 2)下封閉中厚殼(L/2,0)處薄膜內力Nx和彎矩Mx 功率譜密度曲線Fig.4 Response PSD curves of membrane force Nx and bending moment Mx of (L/2,0) for the closed moderately thick shells under random point excitation (case 2)

4.3 隨機環形線激勵作用下中厚圓柱殼振動響應

本節對于上節中討論的半徑R=3.6 m 的封閉中厚圓柱殼,分別取厚度h為0.1 m,0.18 m,0.36 m,也即將厚徑比(h/R)分別取為1/36,1/20,1/10.考慮在封閉中厚殼的環線 (L/2,0～2π)上施加徑向隨機線激勵,該激勵同樣是限帶寬高斯白噪聲,頻帶為[20,2000] Hz,功率譜密度為1 N2/Hz,針對圓柱殼的三種厚徑比情形,采用激勵帶寬內的全部振型參與隨機振動分析(NF分別取為46,27,14).針對上述三種厚徑比,表3 分別給出了中厚殼在(L/2,0)處的徑向位移、速度和加速度均方根.結果表明,在徑向隨機線激勵下,隨著中厚殼厚徑比的增加,結構的抗彎剛度增大,從而導致徑向位移、速度及加速度響應均方根減小.

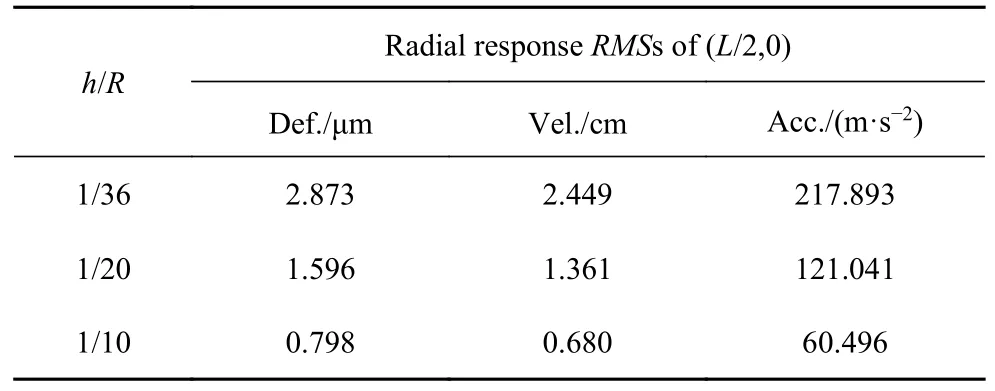
表3 隨機環形線激勵作用下封閉中厚殼(L/2,0)處徑向響應均方根Table 3 Radial response RMSs of (L/2,0) for the closed moderately thick shells under random annular line excitation

而且,也討論了徑向隨機線激勵下中厚殼結構的厚徑比對彎矩均方根的影響.圖5 分別給出了厚徑比為1/36,1/20,1/10 下的中厚殼的彎矩Mx和Mθ的功率譜密度函數.由式(5)可知,彎曲剛度D的表達式中包含厚度的三次方項.在虛擬激勵法中,彎矩響應Mx和Mθ的功率譜密度可由相應的虛擬彎矩與其自共軛相乘,即與D2呈正比.因此,隨著中厚殼厚徑比的增加,彎矩響應Mx和Mθ的功率譜密度隨之增大.

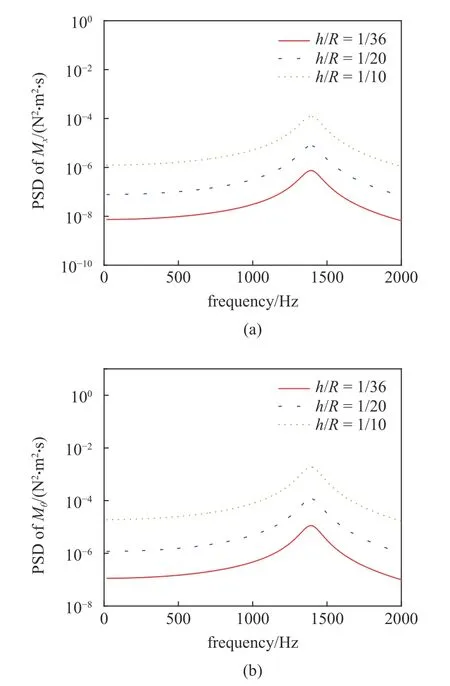
圖5 隨機環形線激勵下中厚殼(L/2,0)處彎矩響應功率譜密度曲線Fig.5 Bending moment response PSD curves of (L/2,0) for the closed moderately thick shells under random annular line excitation

4.4 分布隨機激勵下中厚圓柱殼振動響應

針對4.1 小節討論的開口中厚圓柱殼結構,在其表面施加徑向分布的隨機激勵.考慮激勵具有如下兩類空間分布形式case 1:p1(x,θ)=x;case 2:p2(x,θ)=5θ.隨機激勵為[0,100] Hz 內的限帶寬白噪聲,其功率譜密度Spp=1 Pa2/Hz,采用激勵帶寬內的全部振型參與隨機振動分析(NF=32).阻尼比ζ=0.05.圖6 給出了這兩類分布激勵在開口中厚圓柱殼上的具體空間分布形式.

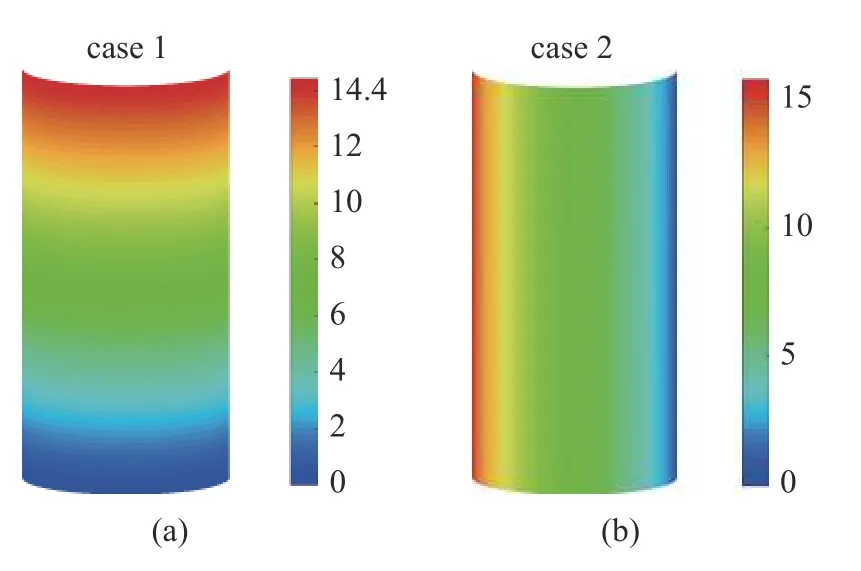
圖6 兩類隨機分布載荷的空間分布形式Fig.6 Spatial distribution forms of two random distributed loads

針對這兩類隨機分布載荷,圖7～圖9 分別給出了開口中厚殼徑向位移、速度及加速度響應的均方根空間分布.對于分布形式case 1 的隨機載荷,其關于θ=π/2 的軸對稱,激勵峰值為x=L=14.4 m.由圖7 (a)、圖8 (a)及圖9 (a)可以看到,位移、速度及加速度響應均方根峰值逐漸向激勵峰值方向移動,這些均方根關于θ=π/2 的軸是對稱的,并且位移、速度響應均方根關于x=L/2 的軸呈現一定的對稱性,而加速度響應均方根關于x=L/2 的軸沒有對稱性.對于隨機載荷case 2,其關于x=L/2 的軸對稱,激勵峰值為θ=φT=π.由圖7 (b)、圖8 (b)及圖9 (b)可知,位移、速度及加速度響應均方根峰值逐漸向θ最大值位置移動,這些均方根關于x=L/2 的軸也是對稱,并且位移、速度響應均方根關于θ=π/2 的軸呈現一定的對稱性,而加速度響應均方根關于θ=π/2 的軸沒有對稱性.其原因在于,與其他空間位置相比,激勵峰值作用位置往往能夠激起結構更高階振型.由式(30)可知,高階頻率對加速度響應影響最大,其次是速度響應.由此可知,由于高階參振振型的影響,激勵峰值作用位置附近的加速度響應均方根出現較大值,導致圖9 (a)、圖9 (b)所示的加速度響應均方根分別關于x=L/2,θ=π/2 的軸呈現非對稱分布.分布隨機激勵的空間分布形式對中厚圓柱殼的加速度響應均方根分布影響較大.由于隨著響應均方根的增大,結構響應的變異性隨之增大.因此在實際工程中,為了保證中厚殼結構在隨機環境激勵作用下的安全性,除徑向位移及速度響應外,應尤其關注結構的加速度響應分布.

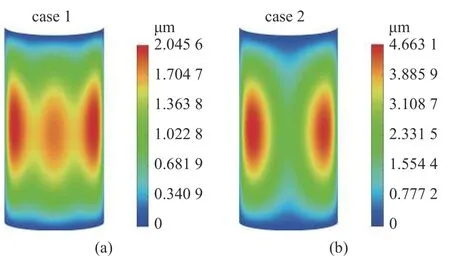
圖7 兩類分布載荷作用下開口圓柱殼的位移響應均方根分布Fig.7 RMS distributions of deflection for open shell under two distributed random loads

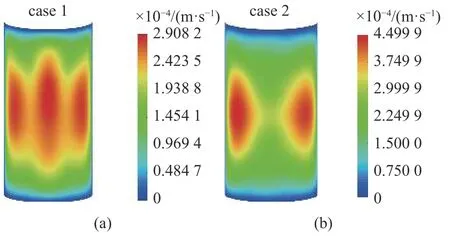
圖8 兩類分布載荷作用下開口殼的速度響應均方根分布Fig.8 RMS distributions of velocity for open shell under two distributed random loads

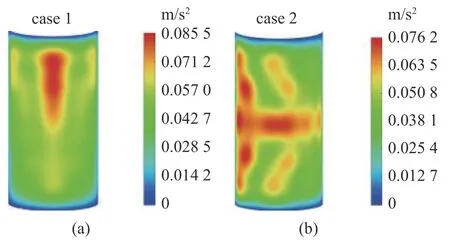
圖9 兩類分布載荷作用下開口殼的加速度響應均方根分布Fig.9 RMS distributions of acceleration for open shell under two distributed random loads

4.5 均勻調制非平穩激勵下中厚圓柱殼振動響應

除平穩隨機激勵外,均勻調制非平穩激勵下中厚圓柱殼的隨機振動響應同樣值得重視.對于如下開口中厚圓柱殼(φT=π,E=27.466 GPa,ρ=7850 kg/m3,L=14.4 m,R=3.6 m,υ=0.2),考慮在開口殼上施加均勻調制非平穩的隨機徑向均布載荷q3(x,θ,t)=f(t)X(t).隨機激勵X(t)假設為[0,100] Hz 內的限帶寬高斯白噪聲激勵,激勵PSDSxx(ω)=1 Pa2/Hz,采用激勵帶寬內的全部振型參與隨機振動分析.

采用如圖10 所示的時間調制函數f(t)[33]

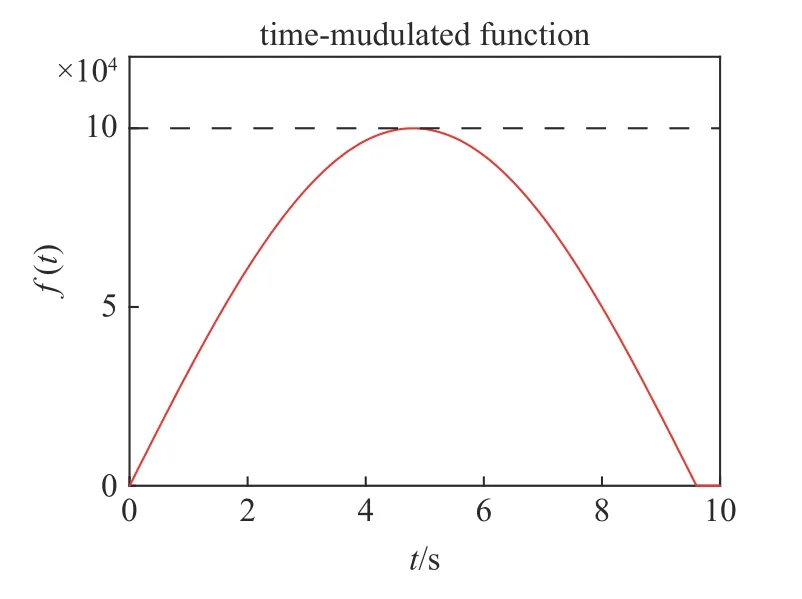
圖10 時間調制函數f(t)Fig.10 Time-modulated function f(t)

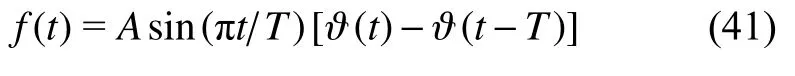
其中,A為時間調制函數幅值,?(t)為Heaviside 函數.本文中,取A=105,激勵持續時間T=9.6 s.可知,t=4.8 s 時,時間調制函數f(t)取最大值.

表4 給出了t=4.8 s 時開口殼中心點(L/2,π/2)處的徑向位移、速度及加速度響應均方根,其中結構厚徑比分別采用1/20和1/10,對應的參振頻率階數NF分別為65和32.為了驗證結果,基于10 000次并行蒙特卡洛模擬(MCS)結果也被給出.利用譜表達方法,隨機激勵描述為

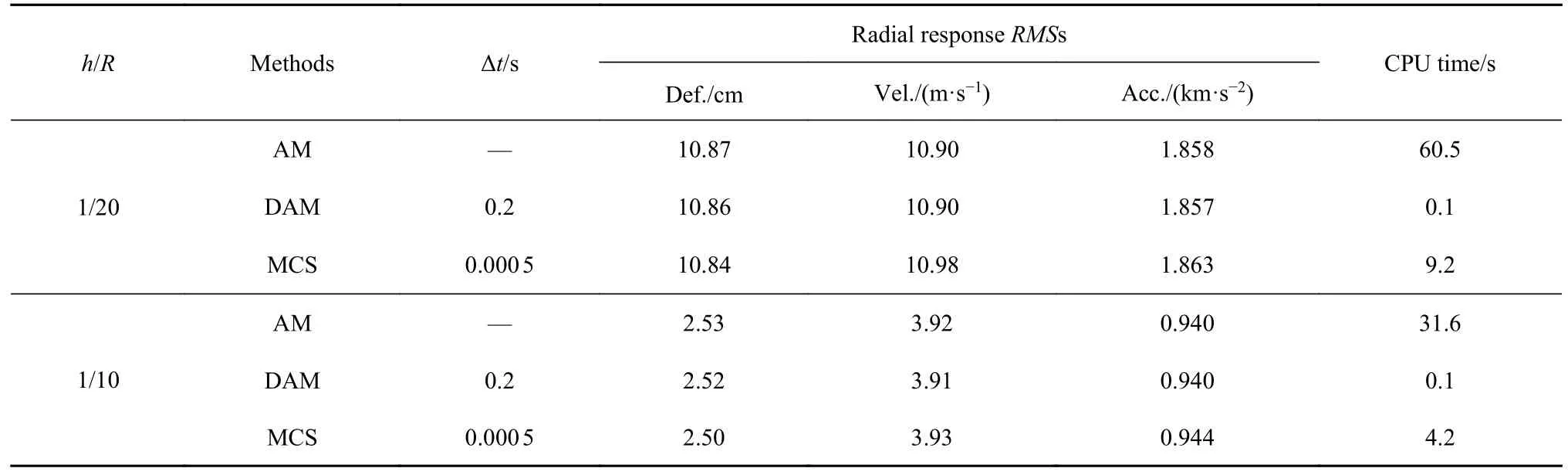
表4 非平穩隨機均布激勵下中厚殼中心點響應均方根 (t=4.8 s)Table 4 Stochastic response RMSs of the center of moderately thick shell under nonstationary random distributed excitations(t=4.8 s)

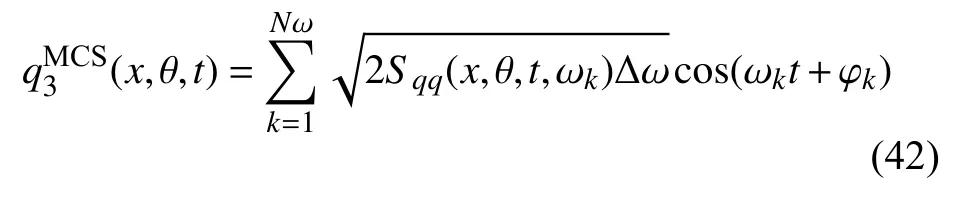
其中,Sqq(x,θ,t,ωk)為非平穩隨機載荷在第k個頻率點的功率譜密度函數,φk是[0,2π]內獨立均勻分布的隨機相位角.對于頻帶[0,100] Hz 的離散頻率點數Nω,離散解析法和蒙特卡洛模擬均將其取為500 以保證公平比較計算效率.此外,若假設0～9.8 s 內f(t)均等于A,則該均勻調制非平穩激勵轉變為平穩隨機激勵.表4 同時給出了中厚殼在該平穩均布激勵下的解析解.可以看到,非平穩隨機振動的離散解析解法在采用精細積分法進行時程分析時,取了較大的時間步長(Δt=0.2 s),得到的計算結果與平穩隨機響應的解析解吻合良好,且計算效率很高.而蒙特卡洛模擬即使時間步長已經足夠小,其計算誤差仍大于離散解析解,這主要歸因于蒙特卡洛的隨機收斂性.此外,從耗費的CPU 計算時間,也可看出,即使蒙特卡洛模擬采用了并行算法,計算效率仍遠低于離散解析法.

非平穩均布激勵下,圖11 分別繪制了厚徑比為1/20和1/10 的兩種情況下位移響應的均方根曲線.可以看到,兩種方法的計算結果吻合良好,但蒙特卡洛模擬曲線存在一定數值振蕩.對于均勻調制非平穩激勵下的中厚殼隨機振動響應,其徑向位移、速度及加速度響應均方根隨時間的變化趨勢與圖10所示的時間調制函數趨勢一致.

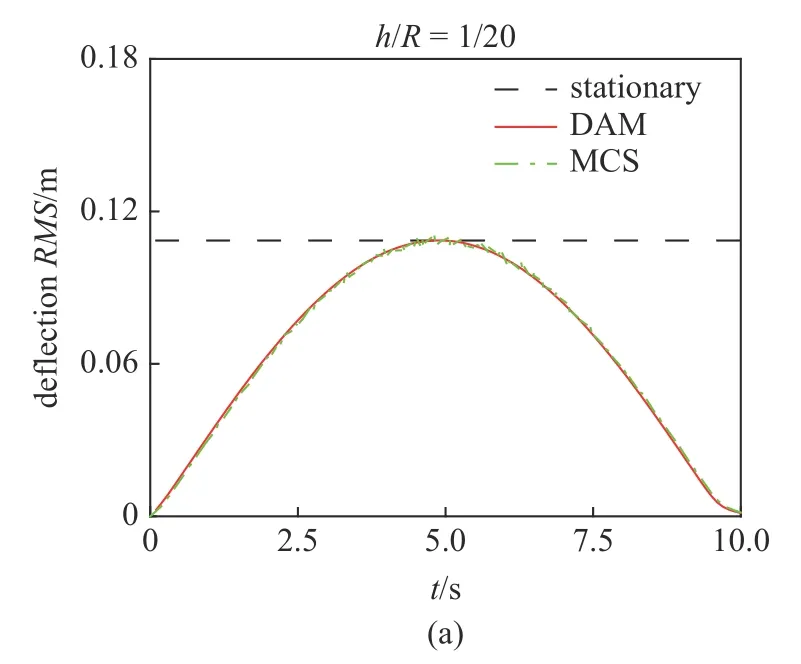
圖11 非平穩隨機激勵下中厚殼中心點位移響應均方根Fig.11 Stochastic deflection responses RMSs of the center of moderately thick shell under nonstationary random excitations

圖11 非平穩隨機激勵下中厚殼中心點位移響應均方根(續)Fig.11 Stochastic deflection responses RMSs of the center of moderately thick shell under nonstationary random excitations(continued)

為了討論開口中厚圓柱殼的厚徑比對位移響應功率譜密度的影響,圖12 分別繪制了厚徑比h/R=1/36,1/20,1/15 下不同時刻(t=4.8 s,t=7 s)的中厚殼中心點處的位移響應功率譜密度曲線.由圖12可知,徑向位移響應的功率譜密度曲線的第一個峰值出現位置從約7.4 Hz 后移到約14.2 Hz.這是由于中厚圓柱殼的基頻隨著中厚殼厚徑比的增加而增大.這表明,在線性隨機振動分析中,結構的自振頻率精確與否將直接影響響應功率譜密度峰值出現的位置.此外,在徑向激勵作用下,中厚殼徑向位移響應功率譜密度的幅值整體減小.因此,隨著結構厚徑比的增加,徑向位移的均方根逐漸減小,也即響應的變異性減小,圓柱殼的安全性得到提高.

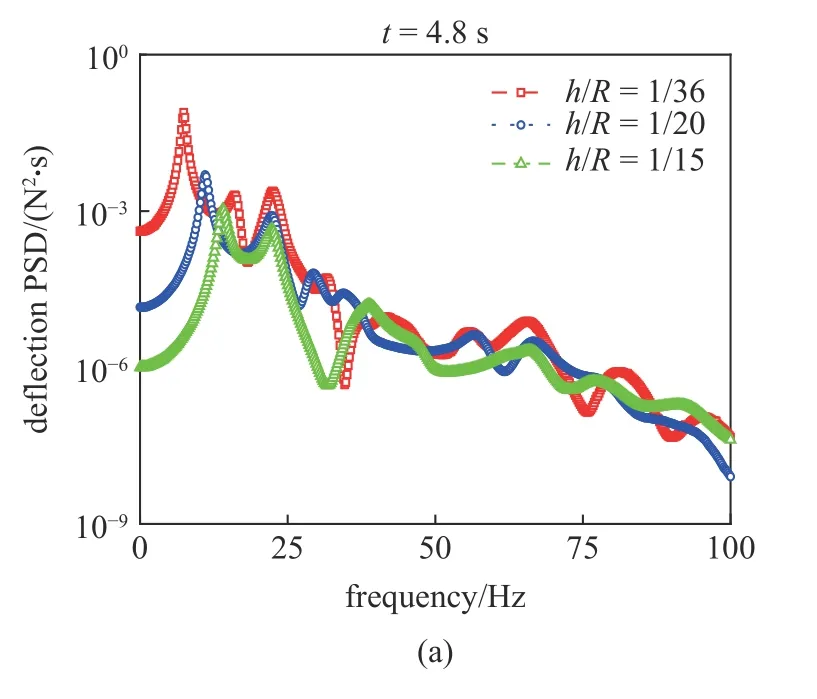
圖12 非平穩隨機激勵下中厚殼中心點位移響應功率譜密度Fig.12 Stochastic deflection responses PSD curves of the center of moderately thick shell under nonstationary random excitations

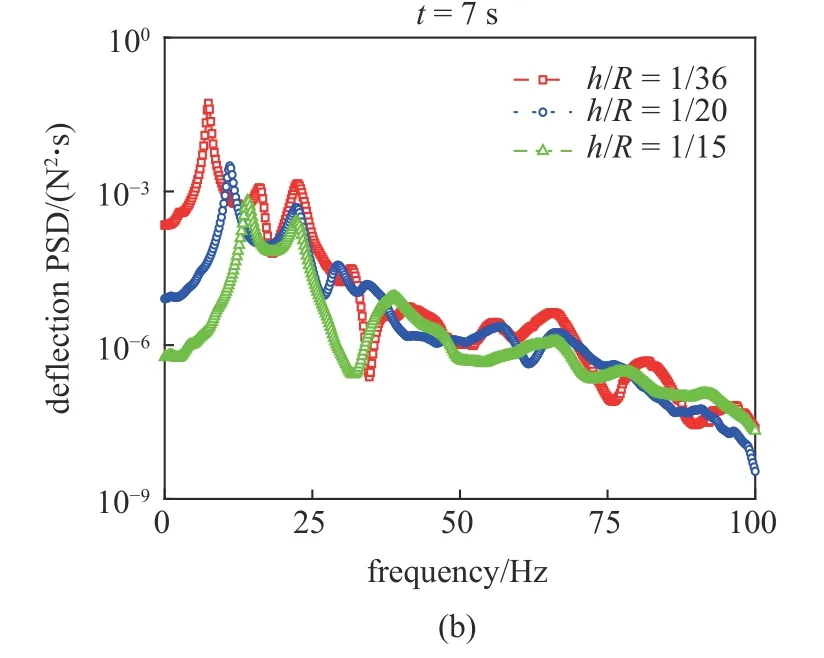
圖12 非平穩隨機激勵下中厚殼中心點位移響應功率譜密度(續)Fig.12 Stochastic deflection responses PSD curves of the center of moderately thick shell under nonstationary random excitations(continued)

5 結論

本文考察了考慮轉動慣量和剪切變形的中厚圓柱殼的隨機振動,獲得了平穩、非平穩隨機振動響應的基準解.通過引入中厚圓柱殼的精確自振頻率和封閉振型函數,基于虛擬激勵法,解析推導了中厚圓柱殼在平穩、非平穩隨機激勵作用下的響應功率譜密度函數.為了充分發揮虛擬激勵法在矩陣運算中的高效性優勢,將空間域積分解析求解,頻域和時域積分數值求解,提出了離散解析法高效計算了中厚殼在各類隨機激勵下響應均方根的基準解.通過與解析解、ABAQUS 軟件結果及蒙特卡洛模擬結果的比較,展示了離散解析法的準確性和高效性.通過算例分析,得到以下主要結論:

(1) 徑向隨機線激勵下,隨著圓柱殼厚度的增加,結構徑向抗壓強度增大,位移、速度及加速度響應均方根等比例降低;結構彎曲剛度增大,導致彎矩響應均方根增加.

(2) 分布隨機激勵的空間分布形式對中厚圓柱殼的加速度響應均方根分布影響較大.為保證結構安全性,中厚殼結構的加速度響應也應受到關注.

(3) 非平穩隨機激勵下,中厚圓柱殼位移響應均方根隨時間變化與時間調制函數相一致.此外,隨著圓柱殼厚度的增加,位移響應功率譜的幅值整體呈減小趨勢,相應的均方根(即變異性)減小,因此結構安全性得到提高.