混凝土動態雙軸拉壓破壞準則細觀數值模擬研究1)

金瀏 李 健 余文軒 杜修力

(北京工業大學城市減災與防災防護教育部重點實驗室,北京 100124)

引言

混凝土是一種拉伸強度較低的脆性材料,其廣泛應用于土木工程中.混凝土的拉伸強度只有其壓縮強度的1/8～1/10[1].當混凝土材料強度降低時,混凝土結構內部產生的裂紋數量逐漸增多,進而降低結構使用壽命.在日常結構設計中,混凝土軸心抗拉強度普遍作為結構計算的安全系數指標之一.如《混凝土結構設計規范》(GB 50010-2010)[2]第7.1.1 條規定,在正常使用極限狀態下對混凝土構件進行裂縫控制驗算時,對于二級裂縫控制等級構件,在載荷標準組合下,受拉邊緣應力應不超過混凝土軸心抗拉強度標準值.從空間受力維度來看,正常服役期內的混凝土結構往往處于復雜應力(雙軸、多軸)狀態中.但是,在雙軸拉壓組合載荷下,混凝土的主軸壓縮強度和側軸拉伸強度均低于其單軸強度[3].Shang 等[3]對不同類型的混凝土在靜態雙軸拉壓載荷下的力學行為進行了研究,得出對于所有類型的混凝土在結構設計和驗算時都應考慮雙軸拉壓載荷下混凝土強度降低的結論.因此,只把混凝土單軸抗拉強度作為結構設計參考值是不安全的,有必要針對混凝土在雙軸拉壓載荷作用下的拉伸強度進一步研究.

通常情況下,普通混凝土結構常處于準靜態載荷下,即應變率≤10-5s-1.但是,混凝土結構不可避免地會受到偶發動力載荷作用.不同的動力載荷作用于結構的應變率范圍不同,如遭到地震時,應變率一般在10-4～ 10-2s-1范圍內;遭到沖擊載荷時,應變率一般在10-2～ 1 s-1范圍內;遭到爆炸載荷時,應變率一般在1～ 103s-1范圍內.混凝土材料在動態載荷下的力學性能較靜載荷下有明顯不同[4-5].但是,目前對于動態載荷下混凝土力學性能的研究,大多集中在動態單軸工況.由于拉伸試驗對試驗設備要求高、開展難度大,目前對于動態雙軸載荷下的混凝土力學行為研究大多集中在動態雙軸壓縮工況,而動態雙軸拉壓工況相對較少且僅處于低應變率范圍內[5].因此,對于動態拉壓載荷下的混凝土力學性能研究尚不充分,亟需進一步研究.

對于混凝土力學性能的研究,破壞準則是基礎.目前,少數學者已經對混凝土雙軸拉壓破壞準則開展了相關研究.表1 列出了目前一些學者所提出的混凝土雙軸拉壓破壞準則.一方面,對于靜態拉壓工況,基于Kupfer 破壞準則[6],文獻[3,5,7-8]考慮側應力比(本文用λ表示)影響,通過真三軸試驗系統研究了不同類型混凝土在靜態雙軸拉壓載荷下的力學行為并提出了不同形式破壞準則.此外,《混凝土結構設計規范》[2]和《日本壩工設計規范》[9]分別對雙軸拉壓破壞準則進行了規范.另一方面,對于動態拉壓工況,Shang和Song[4]開展了不同側應力比和不同應變率下混凝土動態加載試驗,得出混凝土動態側拉強度隨側應力比的增大而增大,隨應變率的增大而增大的結論.文獻[10-12]也得出同樣的結論,并在此基礎上分別提出了不同類型混凝土在動態拉壓工況下的動態破壞準則,如表1 所示.目前,對于混凝土雙軸拉壓破壞準則的研究,處于靜態載荷下的研究較多,而動態載荷下的研究很少.另外,由于試驗設備和條件限制,大多數物理試驗研究范圍處于低應變率(10-5s-1≤≤10-2s-1)和低側應力比(-0.5≤λ≤0)范圍內,在更高范圍內的物理試驗研究目前還幾近空白.近來,細觀數值分析方法為討論混凝土的損傷機理和力學行為提供了一種有效手段.Tine 等[13]和Prasad 等[14]通過數值模擬分析方法研究了混凝土在雙軸拉壓載荷作用下的力學行為并與物理試驗結果進行了對比.吻合良好的對比結果說明合理的數值模擬分析模型可以擴充物理試驗受限的研究范圍.因此,該方法也得到了眾多學者的廣泛應用.

表1 不同學者提出的破壞準則Table 1 Summary of failure criteria proposed by different scholars

綜上,本文應用細觀力學分析模型和數值模擬分析方法,將混凝土材料看作由骨料顆粒、砂漿基質及兩者間的過渡區(interfacial transition zone,ITZ)等介質組成的多相復合材料,研究應變率及側應力比對混凝土動態雙軸拉壓力學行為的影響,并在此基礎上建立靜、動態雙軸拉壓破壞準則.

1 細觀數值模型的建立與驗證

1.1 數值模型與邊界條件

圖1 展示了混凝土三維細觀模型.本文選用邊長D=100 mm 的混凝土立方體試件,將混凝土看作由骨料顆粒、砂漿基質及ITZ 組成的多相復合材料[15-17].假定骨料顆粒為球體,所占體積分數約為40%.采用二級配混凝土,包含兩種骨料粒徑顆粒:中石顆粒粒徑d=30 mm,小石顆粒粒徑d=12 mm.參考文獻[15-17]中的骨料分布表示方法及骨料投放方式建立隨機骨料模型,定義骨料周圍1 mm 厚的薄層區域為界面過渡區.考慮計算量等因素,設置本模型的基本單元尺寸為2 mm 并對局部單元尺寸進行細化.為減緩網格敏感性問題,參考文獻[15-17],在材料達到其峰值強度后采用應力-開裂位移形式的Hordijk[18]模型來替代應力-應變曲線下降段.這本質上使得斷裂能具有唯一性,即與網格尺寸無關,因而可以有效地解決網格敏感性問題.如圖1 所示,為研究動態雙軸拉壓載荷下混凝土的力學行為,本細觀模型的邊界條件設置如下:定義Z軸方向為主軸,在試件頂部設置豎直向下的恒定速度vz=D(為名義應變率),在底部設置豎向固定約束;定義X軸方向為側軸,在試件一側施加水平橫向速度vx=λvz=(λ為側應力比),在對側設置水平固定約束;定義Z軸為自由軸,試件兩側均設置為自由邊界.同時,定義混凝土受拉為正,受壓為負.

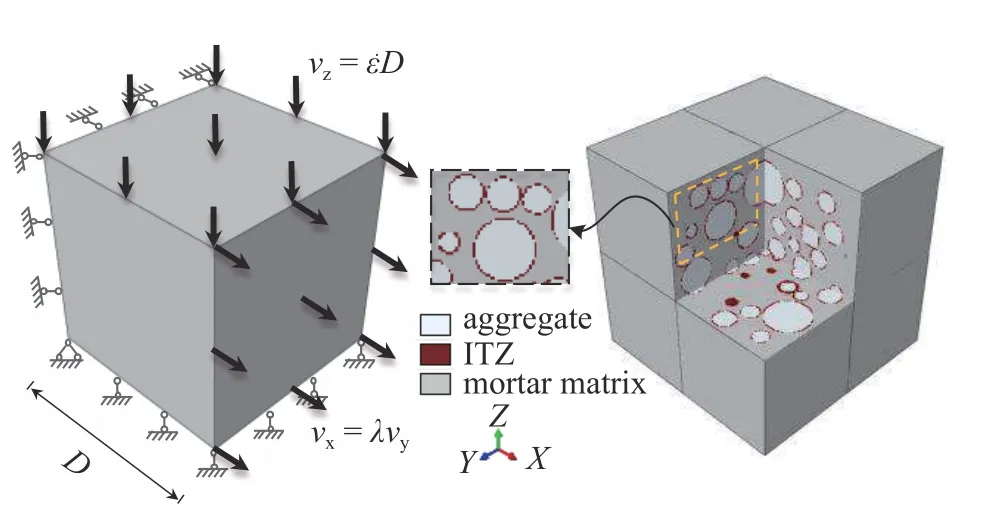
圖1 細觀模型Fig.1 Meso-finite element model

1.2 細觀本構關系

由Lubliner 等[19]首先提出而后由Lee和Fenves[20]進行擴展修正的混凝土塑性損傷(concrete damaged plasticity,CDP)模型目前廣泛應用于混凝土的力學行為細觀模擬中.該模型的核心是假定混凝土材料的破壞形式主要是受拉時開裂破壞和受壓時壓碎破壞.同時,由于混凝土材料損傷而導致的剛度退化和不可恢復的塑性永久變形問題也可由該改進后的CDP 模型表征[19-20],該CDP 模型定義混凝土破壞面主要由等效塑性應變張量 εpl確定,具體應力應變關系可表述為

式中,參數D代表各向同性損傷變量;代表初始無損傷各向同性線彈性張量.

其中,剛度退化因子d分別由兩個獨立的壓、拉損傷變量dc和dt決定.拉、壓剛度損傷因子(均由有)效應力和等效塑性應變來確定,即:

對于改進后的CDP 模型,經典的Drucker-Prager 屈服面函數F可由以下形式表示

特別地,基于以上描述的CDP 模型,Tine 等[13]通過有限元分析方法研究了混凝土類材料在雙軸載荷下的力學行為并且對CDP 模型的可行性進行了試驗驗證.結果表明,CDP 模型可以很好的模擬混凝土類材料在雙軸復雜應力下的破壞演化過程和力學行為,尤其是存在拉伸應力的工況下.以上結果表明,CDP 模型可以較精確地反映出雙軸載荷下混凝土的力學性能和損傷機理.因此,該模型也已被許多學者廣泛使用,如文獻[15-16,21-23].

另外,參考文獻[15-16,24],對于混凝土內部組分,本文同樣僅考慮強度的放大行為,用強度放大因子來表征材料應變率效應,強度放大因子(dynamic increase factor,DIF)即為材料動態強度和靜態強度的比值.在動態雙軸拉壓工況下[10,25],混凝土強度放大因子DIF可以表示為

其中,k是材料參數,反映混凝土材料受壓時的率效應;為靜態應變率;為動態應變率.

參考文獻[15-17],對于描述混凝土內部組分的力學性能可采用如下處理方式:對于砂漿基質,其力學性能與混凝土類似;對于界面過渡區,其可被看作是孔隙率較高的砂漿,因此其力學性能可在砂漿基礎上進行弱化;對于骨料顆粒,在動態載荷下,混凝土內部骨料并不都是彈性體,而是會在應變率作用下被拉斷或劈裂,其力學性能可在砂漿基礎上進行強化.因此,對于本研究中混凝土的三相內部組分,均采用上述考慮應變率效應的CDP 模型來表述其力學性能,這種處理方法的可行性已得到了商懷帥[26]和申佳玉[27]等學者的物理試驗驗證.

1.3 數值模型驗證

在本節中,將用上述建立的細觀數值模型對Shen 等[10]開展的動態雙軸拉壓試驗進行驗證,以此來驗證細觀數值模型的可行性.表2 列出了本文所采用的混凝土各細觀組分的具體力學參數.其中,混凝土的立方體壓縮強度,密度和彈性模量等物理參數參考Shen 等[10]的物理試驗,泊松比υ和其他物理參數并未給出,本文的確定方法參考了文獻[15-17].至于界面過渡區的壓縮強度等物理參數,參考文獻[15-17],采用反復試算的方式具體確定.采用以上力學參數進行細觀數值模擬得到的最終混凝土破壞模式、主軸壓縮強度和側軸拉伸強度分別與Shen 等[10]物理試驗結果的對比如圖2 所示.

表2 數值模擬中使用的物理參數Table 2 Mechanical parameters used in simulations

圖2 數值模擬結果與試驗[10]的對比Fig.2 Comparison of numerical results and test [10]

2 結果與分析

為了研究混凝土動態雙軸拉壓強度及破壞準則,本研究設置中、低兩個應變率范圍(低應變率:=10-5s-1,10-3s-1和10-2s-1;中應變率10-1s-1和1 s-1) 以及不同側應力比λ=0(單軸壓縮),-0.25,-0.50,-0.75,-1.00和-∞(單軸拉伸)共計30 種工況,對尺寸為D=100 mm 的立方體混凝土試件進行了靜、動態雙軸拉壓數值模擬研究.本研究采用有限元分析軟件ABAQUS 中的顯式算法.每個試件包含約1.4 × 105個計算單元,計算成本3～ 5 h.

2.1 破壞模式

圖3 展示了應變率和側應力比對混凝土破壞模式的影響.可以看出,在低應變率范圍內(10-5s-1≤≤10-2s-1),不同側應力比下的混凝土內部破壞模式相似.具體體現為試件內部較為薄弱的區域(ITZ)首先破壞然后擴展到砂漿基質.隨著損傷區域不斷擴展,最終形成主要沿骨料和砂漿的黏結面劈開的拉斷面,并且試件的破壞面上被拉斷的粗骨料較少.在中應變率范圍內(10-2s-1≤≤1 s-1) 破壞面上被拉斷的粗骨料的數量增多,混凝土內部損傷變大,并且裂紋數量增加.這是由于當應變率較大時,混凝土試件內部破壞響應較迅速,側拉力直接作用于骨料,導致破壞面不再沿ITZ 擴展到砂漿基質最后穿過骨料展開.另外,從圖3可以看出,在不同工況下,側應力比對于混凝土材料內部組分破壞的影響要遠小于應變率效應.

圖3 不同工況下混凝土破壞模式Fig.3 Failure modes of concrete under different loading conditions

2.2 混凝土強度

圖4 展示了不同工況下的混凝土動態主軸壓縮強度和側軸拉伸強度.可以看出,混凝土動態主軸壓縮強度和側軸拉伸強度均隨應變率的增大而增大.但是,隨側應力比增大,動態主軸壓縮強度減小,而側軸拉伸強度增大.這是由于逐漸增大的拉應力使側向約束能力逐漸降低,從而加速了裂縫擴展,削弱了耗能能力,最終導致主軸壓縮強度下降.同時,隨著側應力比增大,混凝土內部在側拉力反向形成的抵抗力逐漸增大,導致內部損傷區域和裂縫數量增多,從而耗散了更多的能量,因此,混凝土側軸拉伸強度也隨之增大.

圖4 不同工況下混凝土雙軸強度Fig.4 Biaxial strength of concrete under different loading conditions

2.3 試驗結果對比

為了驗證以上數值模型的合理性以及試驗結果的準確性,本節將數值模擬得到的強度數據點與文獻[5,10,28-29]的物理試驗強度數據點進行了對比.

圖5 為不同工況下主軸壓縮強度數據點和試驗結果的對比.由于不同試驗所選取的混凝土強度不同,這里暫且采取歸一化處理來進行對比,即(動態主軸壓縮強度/靜態單軸壓縮強度).通過圖5所示的對比結果可以看出,主軸壓縮強度數據結果的變化趨勢與試驗結果的保持一致.

圖5 主軸壓縮強度數據點與試驗結果的對比Fig.5 Comparison of spindle compressive data and test results

圖6 為不同工況下側軸拉伸強度數據點和試驗結果的對比.同樣地,這里采用統一標準(DIF)來進行對比.通過圖6可以看出,本文模擬得到的側軸拉伸強度數據結果在不同試驗的數據點變化范圍內,這進一步說明了以上數值模擬結果的準確性.

圖6 側軸拉伸強度數據點與試驗結果的對比Fig.6 Comparison of lateral tensile data and test results

3 混凝土雙軸拉壓破壞準則

目前,對于雙軸拉壓載荷下的混凝土破壞準則,大多數研究主要集中在靜態工況下展開,而對考慮應變率影響的動態破壞準則研究較少.本節主要從靜態和動態兩個角度來討論混凝土雙軸拉壓破壞準則.

3.1 靜態破壞準則對比

如表1 所示,對于靜態雙軸拉壓載荷下的混凝土破壞準則,不同學者提出的破壞準則具有相似的比例關系[2-3,5-9],即

因此,本文將數值模擬數據點與不同學者的物理試驗數據點[2-10,30-35]進行了對比,如圖7 所示.通過對比可以看出,在靜態雙軸拉壓工況下,本文數值模擬結果的變化趨勢與不同物理試驗點的變化趨勢基本一致.另外,參考式(12)對本文數值模擬結果進行擬合,得到了如圖7 所示的函數關系式.在本文中,參數c=1.050.同時,從圖7可以看出,張麗等[8]和劉學波[31]的物理試驗點基本在本文的擬合曲線上,這也進一步驗證了本文數值模擬結果的準確性.

“a slender hand”對應著“一只玉手”，“玉手”一詞指的是女性的手潔白如玉，是對他人之手的敬稱。“玉”是“美，尊貴的，敬辭”的含義。在中國，有玉手、玉足之說，故此處筆者認為譯文不妥。

圖7 靜態雙軸拉-壓強度破壞準則Fig.7 Failure criterion of static biaxial tensile-compressive strength

3.2 動態破壞準則建立

通過表1可以看出,對于動態雙軸拉壓載荷下的混凝土破壞準則,式(11)將不再適用,并且動態載荷下的雙軸拉壓破壞準則尚沒有統一的準則關系式.為了進一步驗證本文模擬結果的準確性,本文首先將數值模擬數據點與不同物理試驗點[10,35]進行了對比,如圖8 所示.可以看出,本文得到的混凝土動態雙軸強度變化趨勢是合理的.

圖8 動態雙軸拉-壓強度與試驗結果的對比Fig.8 Comparison of dynamic biaxial tensile-compressive strength and test results

如前節所述,動態雙軸拉壓載荷下,應變率和側應力比是影響混凝土強度的主要影響因素.但是,由表1可知,目前已提出的不同形式動態破壞準則存在以下幾個問題:

(1)形式較為復雜;

(2)應變率和側應力比研究范圍集中在低應變率(10-5s-1≤ε˙ ≤10-2s-1)和低側應力比(-0.5 ≤λ ≤0)的范圍,缺乏更高應變率和側應力比范圍;

(3)未能綜合反映應變率和側應力比的耦合作用.

因此,本節將針對以上問題開展研究與討論.參考文獻[10,35],動態雙軸拉壓破壞準則可以通過側軸拉伸強度比、應變率和側應力比λ來表示,這種表示方法可以同時反映應變率和側應力比的耦合效應.

首先,考慮應變率對混凝土強度的影響,文獻[10,25]對試驗數據進行回歸分析,得到了側軸拉伸強度和應變率之間的關系為(研究范圍:應變率10-5s-1≤≤10-2s-1)

圖9 不同側應力比下式(13)的擬合結果Fig.9 Fitting results of Eq.(13) under different lateral stress ratios

然后,考慮側應力比對混凝土強度的影響,初步分析不同工況下側應力比和側軸拉伸強度之間的關系,如圖10 所示.參考文獻[10]的工作,這里選取指數函數進行回歸分析.由圖10可知,該函數關系可以較好的反映混凝土強度與側應力比間的變化關系.因此,可以提出側軸拉伸強度和側應力比之間的關系式為

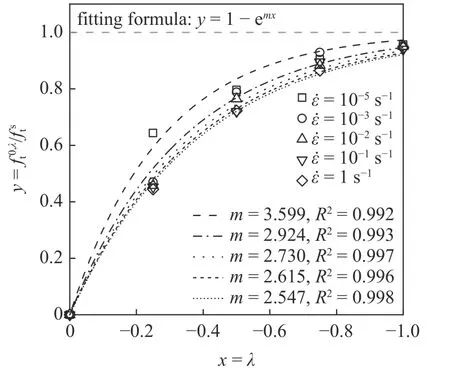
圖10 不同應變率下式(14)的擬合結果Fig.10 Fitting results of the Eq.(14) under different strain rates

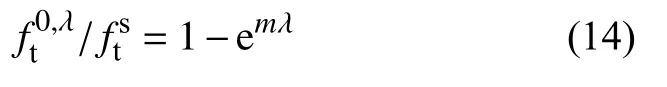
式中,為不同側應力下混凝土動態側軸拉伸強度;m為擬合參數.本文不同工況下對式(14)的擬合結果如圖10 所示.可以看出,隨著應變率增大,參數m逐漸減小.

最后,綜合式(13)和式(14)可得到動態雙軸拉壓工況下,考慮應變率和側應力比影響的混凝土雙軸拉壓破壞準則

其中,K1,K2,K3和m為擬合參數.

3.3 破壞準則驗證

為了進一步驗證上述提出的混凝土動態雙軸拉壓破壞準則的合理性和準確性,本節選取了文獻[5,11]的物理試驗數據來與式(15)進行擬合與對比.不同試驗工況下得到的式(15)中各參數擬合結果如表3和表4 所示.由擬合結果可以得出,式(15)中的參數K3可在不影響擬合公式結果的基礎上進一步精煉為K3=1.00,這進一步簡化了混凝土動態雙軸拉壓破壞準則.

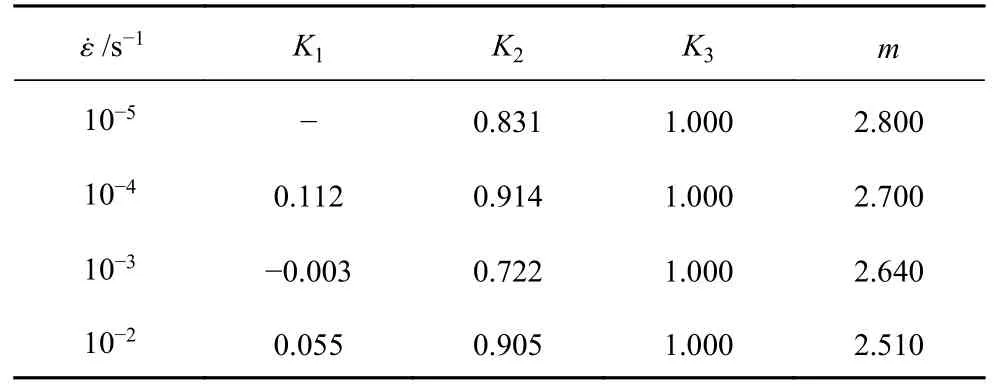
表3 與文獻[5]對比得到的式(15)各參數擬合結果Table 3 Fitting results in Eq.(15) comparing with Ref.[5]

表4 與文獻[11]對比得到的式(15)各參數擬合結果Table 4 Fitting results in Eq.(15) comparing with Ref.[11]

圖11和圖12 展示了不同工況下由動態雙軸破壞準則得到的擬合值與文獻[5,11]的物理試驗值的對比結果.可以看出,在不同工況下,由相應參數擬合得到的擬合值與文獻[5,11]的試驗值均吻合良好,這證明了上述提出的混凝土動態雙軸拉壓破壞準則的可行性和準確性.另外,通過試驗數據的對比,進一步得到了精煉后的混凝土動態雙軸拉壓破壞準則,即

圖11 破壞準則擬合值與文獻[5]試驗值的對比結果Fig.11 Comparison between the fitted data and the experimental data of Ref.[5]

圖12 破壞準則擬合值與文獻[11]試驗值的對比結果Fig.12 Comparison between the fitted data and the experimentaldata of Ref.[11]

需要說明的是,受物理試驗設備和條件限制,目前可收集到的物理實驗數據點僅處于低應變率、低側應力比范圍內.因此,本文只能暫且在此范圍內對動態雙軸拉壓破壞準則的合理性進行了驗證,對于更高范圍的物理試驗驗證工作將在未來開展.

4 結論

本文建立了混凝土立方體三維隨機細觀數值模型,研究了在不同應變率和側應力比下混凝土動態雙軸拉壓的破壞行為,分別討論了應變率和側應力比對混凝土動態雙軸強度的影響,總結提出了混凝土動態雙軸拉壓強度破壞準則,具體結論如下.

(1)混凝土內部組分破壞模式隨應變率增大而呈現不同形式.中應變率范圍內混凝土內部骨料破壞較多,損傷區域較大.

(2)在不同工況下,混凝土動態主軸壓縮強度和側軸拉伸強度均隨應變率的增大而逐漸增大.但是,動態主軸壓縮強度隨側應力比增大而減小,而側軸拉伸強度隨側應力比增大而增大.

(3)本文提出的混凝土動態雙軸拉壓強度破壞準則與現有研究成果相比,擴大了應變率和側應力比的適用范圍,凝練了破壞準則復雜的形式,考慮了應變率和側應力比的耦合作用,并且得到了不同角度的驗證.