一道競賽試題的多解及推廣

福建省福清第一中學(xué) (350300) 葉誠理福建省福清第三中學(xué) (350315) 何 燈

1.試題賞析

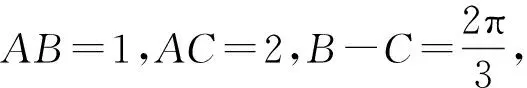
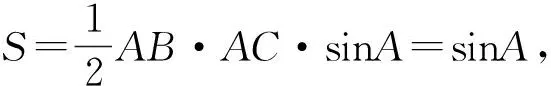
2.試題解析

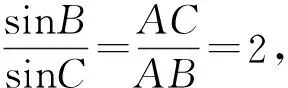
評注：本解法通過正弦定理把邊b,c的關(guān)系轉(zhuǎn)化成角度B,C的關(guān)系，結(jié)合三角形內(nèi)角和關(guān)系，運(yùn)用三角恒等變換公式，轉(zhuǎn)化成與角C相關(guān)的三角函數(shù)計算問題.

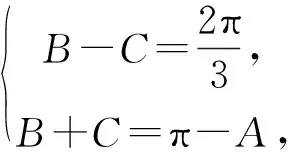
評注：本解法仍然是通過正弦定理把邊的關(guān)系轉(zhuǎn)化成角的關(guān)系，與解法一不同之處在于通過聯(lián)立角A,B,C的關(guān)系，把角B,C統(tǒng)一用角A表示，從而得到關(guān)于角A的三角關(guān)系式，體現(xiàn)了消元、方程思想在解三角形中的應(yīng)用.

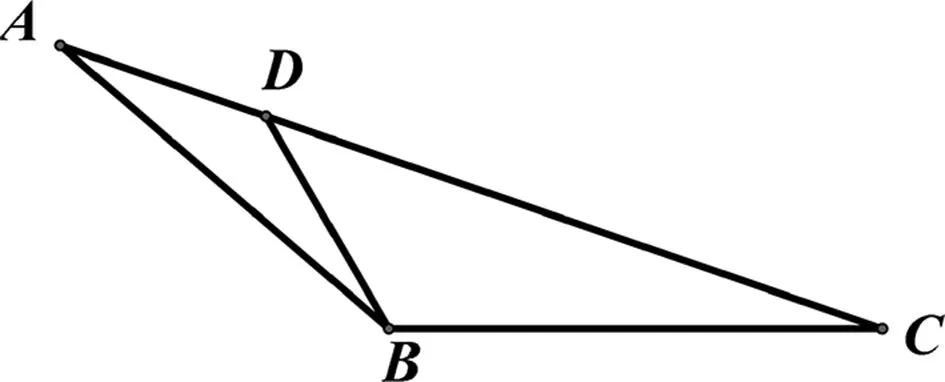
圖1

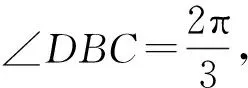
評注：本解法通過添加輔助線將角B分解為兩個角，從而構(gòu)造兩個三角形相似，利用余弦定理構(gòu)建邊a的方程，實現(xiàn)了面積的轉(zhuǎn)化計算.

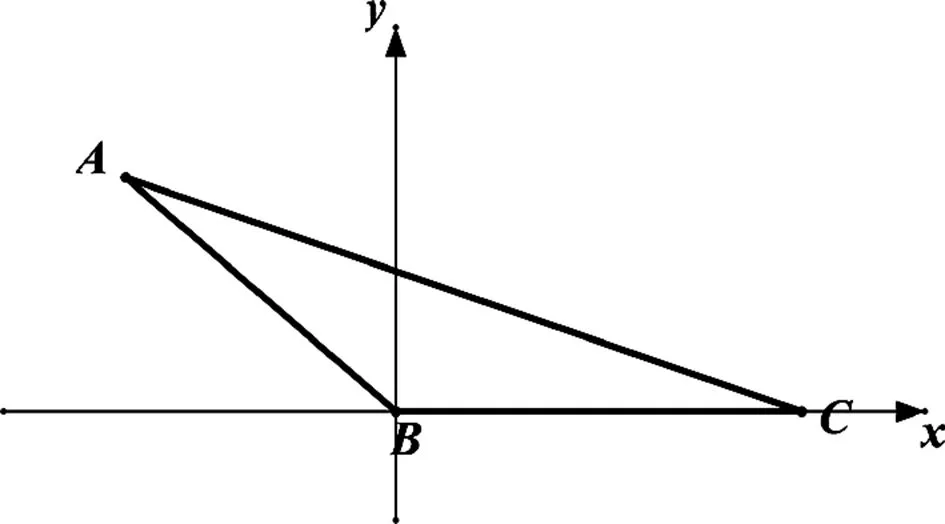
圖2

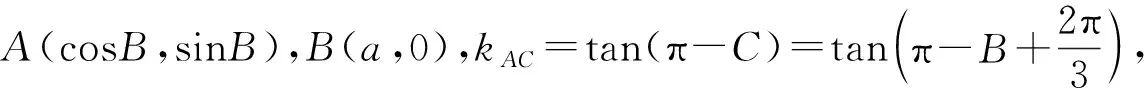
評注：本解法通過建立坐標(biāo)系實現(xiàn)把解三角問題運(yùn)用解析幾何知識來求解.關(guān)鍵是幾何條件代數(shù)化，其中，以B為原點的好處是可以根據(jù)AB=1把點A看單位圓上點，用角B巧設(shè)點A坐標(biāo)，利用直線AC斜率表達(dá)式，把邊a關(guān)系轉(zhuǎn)化成角B的三角函數(shù)，進(jìn)而通過AC距離公式計算sinB，最終轉(zhuǎn)化成面積.

3.試題推廣

借鑒解法二的證明，我們可以得到更一般的結(jié)論.

推廣在△ABC中，AB=c，AC=b，其中b>c且B-C=α>0，則△ABC的面積為