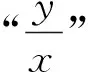構造齊次式巧解解幾中的斜率之和(積)問題

江蘇省如皋中學 (226500) 曹春茂

分析、解決直線與圓錐曲線交匯中，具有公共點的兩條直線的斜率之和或斜率之積問題時，我們經(jīng)常采用的就是“設而不求”技巧，對字母形式的代數(shù)運算以及推理能力的要求較高.為了簡化運算，優(yōu)化解題思維過程，現(xiàn)給出一種具有創(chuàng)新性的方法——在適當建立新的平面直角坐標系的基礎上，借助“構造齊次式”，可巧妙處理此類問題.這種創(chuàng)新方法能夠引導我們不斷探索新穎別致的解法，培養(yǎng)探索精神，同時可幫助我們提升數(shù)學核心素養(yǎng).

典型問題已知P是平面內(nèi)的一個定點，圓錐曲線C上有兩動點A,B，證明：直線PA與PB斜率之和(或積)為定值.

解題步驟：(1)在公共點P處建立新的平面直角坐標系(橫軸與原來的橫軸平行或重合，正方向相同；縱軸與原來的縱軸平行或重合，正方向相同)，則可將原問題等價轉(zhuǎn)化為在新系下，證明直線PA與PB斜率之和(或積)為定值.

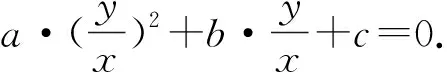
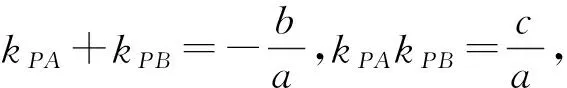
特別注意：若給定直線PA與PB斜率之和(或積)為定值，證明直線AB恒過定點.需要先在新系下，證明直線AB恒過定點；再在原坐標系下，具體分析定點的坐標.

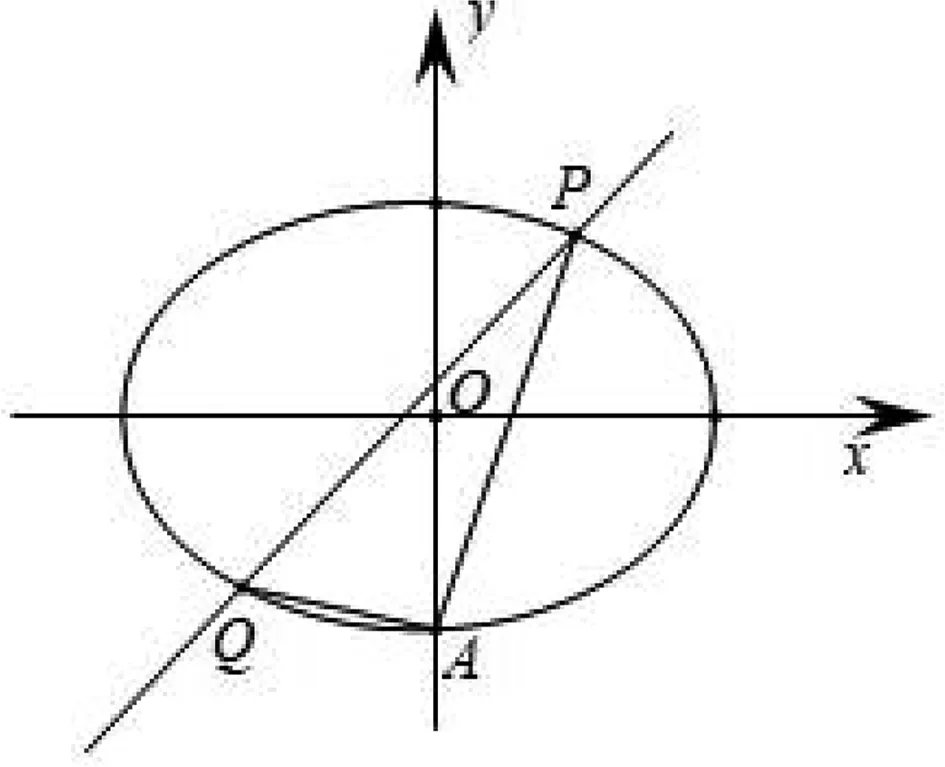
圖1

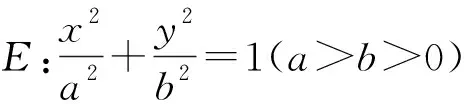
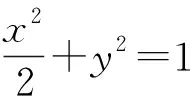
(2)當直線PQ經(jīng)過坐標原點時，易知直線AP與AQ斜率之和為2.

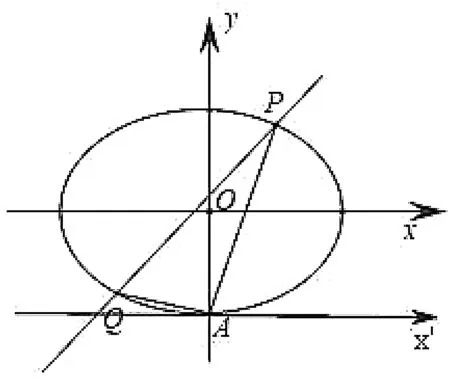
圖2

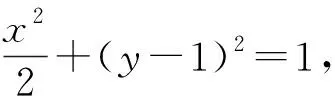
在新系下，設直線PQ的方程為mx+ny=1，則根據(jù)直線PQ經(jīng)過點(1,2)可得m+2n=1.

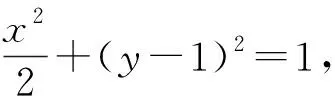
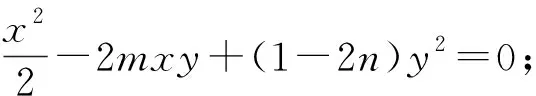
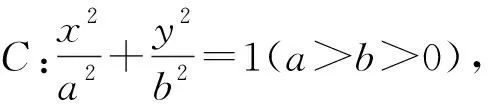
(1)求C的方程；(2)設直線l不經(jīng)過P2點且與C相交于A,B兩點，若直線P2A與直線P2B的斜率的和為-1，證明：l過定點.

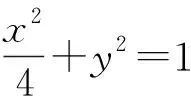
(2)先分析直線l不經(jīng)過坐標原點的情形.

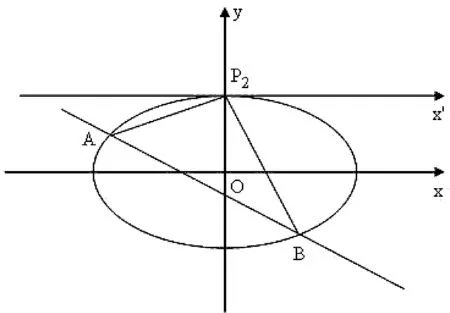
圖3

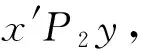
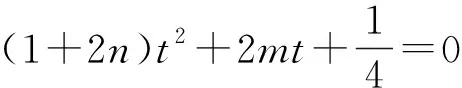
評注：第(2)問巧解，首先是在新坐標系下，通過“構造齊次式”，結(jié)合題設得到參數(shù)m,n滿足的關系式2m-2n=1，進而得到直線l過定點(2,-2)；然后回歸到原坐標系下，即可順利獲得直線l過定點(2,-1).

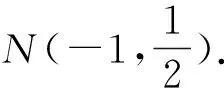
(1)求拋物線的方程；(2)已知C(0,-2)，若直線y=kx+2與拋物線交于A,B兩點，記直線CA,CB的斜率分別為k1,k2，求證：k1k2+k2為定值.

解析：(1)易得拋物線方程為x2=2y(過程略).

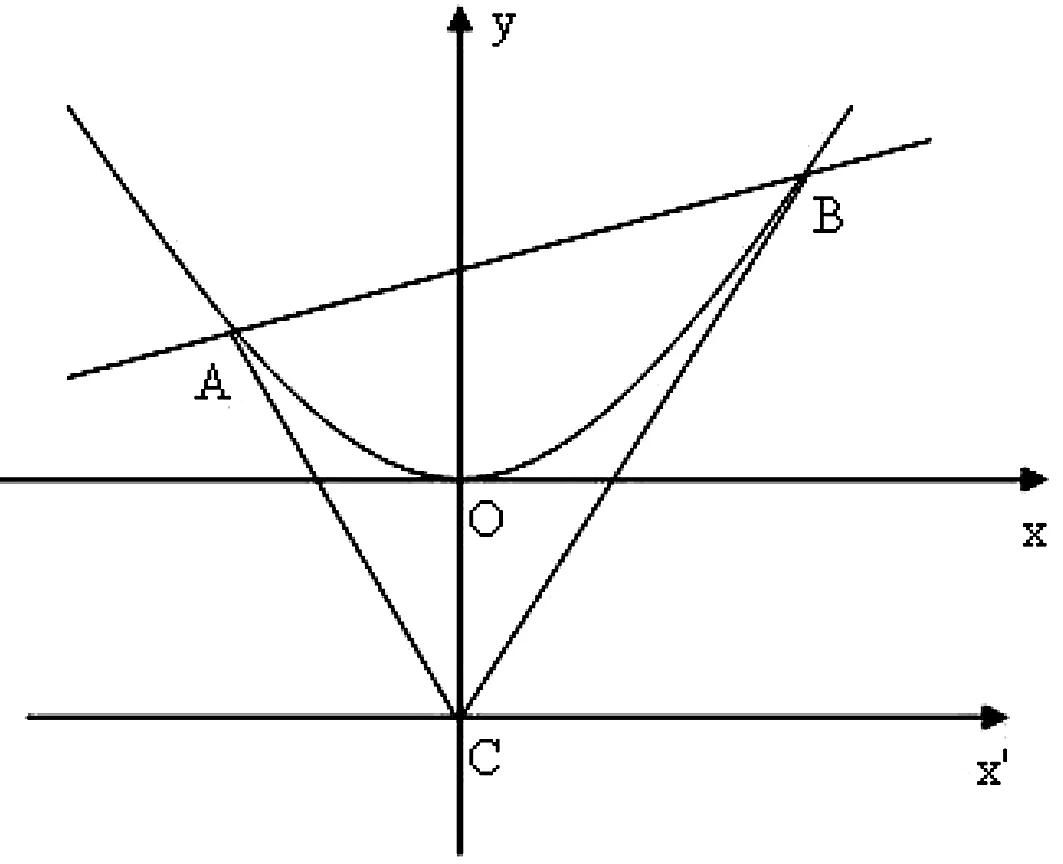
圖4

(2)如圖4，在點C處建立新的直角坐標系x′Cy，則在新系下拋物線方程為x2=2(y-2).易知直線AB不經(jīng)過坐標原點.

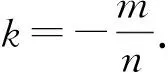
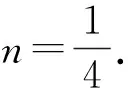
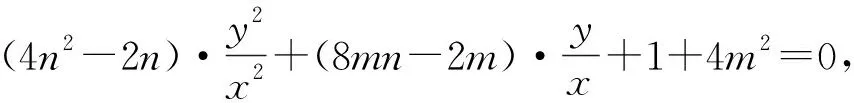
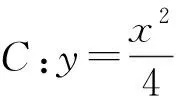
(1)求直線AB的斜率；(2)設M為曲線C上一點，C在M處的切線與直線AB平行，且AM⊥BM，求直線AB的方程.

解析：(1)直線AB的斜率為1(過程略).

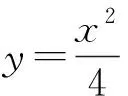
若直線AB經(jīng)過坐標原點，則易知A與B的坐標分別為(0,0),(4,4)，又因為點M(2,1)，所以易檢驗知此時AM⊥BM不成立，從而必有直線AB不經(jīng)過坐標原點.

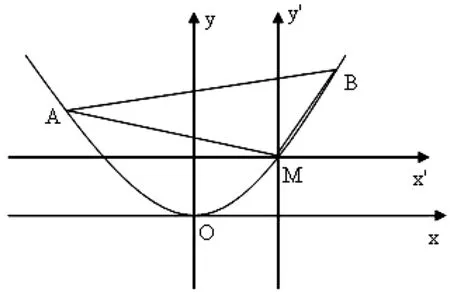
圖5

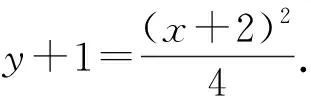
在新系下，設直線AB的方程為mx+ny=1.

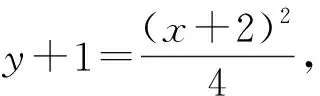
評注：一般地，若在點(a,b)處建立新的平面直角坐標系，則原來的拋物線x2=2py，在新系下拋物線的方程為(x+a)2=2p(y+b)；新系下的曲線方程f(x,y)=0，在xOy坐標系下曲線方程變?yōu)閒(x-a,y-b)=0.