地鐵扣件e型彈條受載特征分析

吳浩，韋凱，郭恭兵，薄棟乾，王平

(1.西南交通大學 高速鐵路線路工程教育部重點實驗室，四川 成都 610031；2.西南交通大學 土木工程學院，四川 成都 610031)

扣件系統是軌道結構中的重要組成部分，彈條作為扣件系統中的關鍵部件，起到固定鋼軌的作用。近年來，隨著列車運營速度的提高，彈條斷裂破壞的現象時有發生，且多伴隨有鋼軌波磨病害，嚴重危及行車安全。針對扣件彈條的受載特征分析，目前已有相關研究。陳憲麥等[1-4]計算分析了e 型彈條在服役條件下的受力狀態，發現mises 等效應力集中區域出現在小圓弧內側，且最大等效應力為小圓弧內側靠近彈條跟端位置。在此基礎上，尚紅霞等[5]采用有限元方法分析了e 型彈條安裝狀態下的受載規律，認為彈條異常斷裂的原因是彈條中肢插入鐵墊板孔長度過深，當彈條小圓弧與鐵墊板端部距離在2 mm 以內時，導致彈條與鐵墊板孔端部擠壓并產生應力集中。周華龍等[6]對某地鐵線路彈條安裝間隙的情況進行隨機抽樣檢測，發現安裝間隙在6～13 mm 之間，表明彈條過安裝可能是導致彈條異常斷裂的原因之一，但是經過現場調查發現，彈條安裝間隙在2 mm 以內的過安裝情況并不多見。因此，有必要對扣件彈條在正常安裝狀態下的受載特征進行深入研究。同時，考慮到彈條斷裂地段普遍伴隨鋼軌波磨病害的現象，目前已有學者進行了相關研究。王開云等[7]分析了扣件系統的垂向振動特性，并與實測結果進行對比驗證，發現鋼軌波磨對彈條的振動特性產生不利影響。肖宏等[8]采用時頻域響應分析方法研究了波磨對彈條的激振影響，研究結果表明，彈條固有頻率與波磨通過頻率一致引發共振，是導致彈條折斷的主要外因。金屬材料的斷裂損傷與應力狀態存在重要關系[9]，目前對于e 型彈條應力狀態的分析研究均是基于第四強度理論，然而基于第四強度理論判斷的彈條斷裂破壞危險點與現場斷裂位置不一致。隨著材料失效破壞的深入研究，許多材料宏觀脆斷的現象，對于傳統強度理論破壞準則的概念不再適用。人們在金屬材料斷裂機理的研究中，提出了應力狀態參數的概念。國內外學者基于應力狀態參數與材料失效的關系開展了大量試驗[10-16]，證明了材料的失效參量明顯依賴于應力狀態參數。鑒于此，本文作者應用應力狀態參數，反映彈條在服役條件下的受載特征，并在此基礎上計算分析彈條在第1階固有頻率共振時的應力狀態，科學探究e型彈條在鋼軌波磨激勵條件下發生異常脆性斷裂的原因。

1 現場調研

某地鐵線路設計時速120 km/h，線路涵蓋高架線與地下線，高架線鋪設DTⅢ型小阻力扣件系統，扣件彈條為e 型常阻力彈條；地下區間鋪設DTⅢ型小阻力扣件系統，扣件彈條為e 型小阻力彈條。該線自開通運營半年后出現了扣件彈條斷裂失效問題，并伴隨出現鋼軌波磨病害，為線路運營造成了安全隱患。根據彈條傷損情況統計結果顯示，斷裂多為脆性斷裂。折斷形式主要為前拱小圓弧和彈條中肢連接處斷裂，占比86%，如圖1(a)所示，也有部分彈條在前拱大圓弧與跟端連接處發生斷裂，占比14%，如圖1(b)所示。

圖1 現場彈條斷裂情況Fig.1 Fracture condition of clip on site

運營現場對波磨較為嚴重的區段進行了測試，測試結果發現，鋼軌波磨主要波長范圍為31～40 mm，對應的波磨通過頻率范圍715～923 Hz，與e 型彈條正常安裝狀態下第1 階固有頻率重合。扣件彈條在鋼軌波磨引起輪軌高頻激勵條件下發生共振，進而誘發彈條異常脆性斷裂問題。

2 應力狀態參數

在損傷斷裂機理研究中，應力狀態參數常用來描述金屬材料的塑性變形規律和損傷斷裂情況。它簡明的表達式也能方便地應用于有限元計算結果后處理中。本文應用3 種常見的應力狀態參數，分別為應力三軸度Rd，應力軟性系數α和羅德參數μd，如式(1)～(3)所示。

在針對脆性斷裂問題的研究中，SIH 等[17-18]提出最大周向應力理論和應變能密度因子理論。RICE[19]基于以上思想，定義了應力三軸度，即靜水壓力與等效應力之比，它通常被用作表征三軸應力狀態影響的重要參數，并且可以用來預測構件損傷斷裂的危險位置。對于金屬材料，應力三軸度增大的區域內易于產生裂紋，并且會導致材料延性降低。JOHNSON 等[20]提出了著名的J-C 斷裂準則，認為材料的斷裂應變隨著應力三軸度的增大而降低。在此基礎上，BAI等[21]考慮了羅德參數對斷裂應變的影響，提出了MMC 準則。羅德參數可以反映應變類型，羅德參數大于0的區域產生壓縮類應變,反之將產生伸長類應變[22]。軟性系數α[23]是描述應力狀態軟硬程度的參數。材料中軟性系數越小，表示應力狀態越硬，金屬易于產生脆性斷裂，反之，材料易產生塑性變形，發生韌性斷裂。

式中：σ1，σ2，σ3分別為第1，第2和第3主應力；μ為泊松比。

3 e型彈條有限元模型建立

3.1 有限元模型

e 型常阻力和小阻力彈條設計彈程均為13 mm，2 種e 型彈條幾何形態近似，經計算后發現2種彈條在正常安裝條件與共振條件下應力狀態基本保持一致，因此本文以e型常阻力彈條為例進行分析，基于地鐵常用扣件DTⅢ型扣件系統研究e 型彈條的失效斷裂問題，建立e 型彈條有限元精細化模型。

e 型彈條安裝狀態下邊界條件及其受力狀態復雜。因此有必要建立精細化三維模型并考慮扣件系統各部件之間摩擦接觸，以反映e型彈條扣件系統的真實受力情況。為了提高計算效率，只取單側e型彈條，軌距擋塊及其與彈條接觸的鐵墊板局部進行建模分析。有限元模型單元類型選用四面體實體單元。通過多次計算比較分析，確定e型常阻力彈條模型共劃分739 97 個網格和15 343 個節點，e 型小阻力彈條模型共劃分104 187 個網格和155 388 個節點，扣件系統精細化模型如圖2所示。

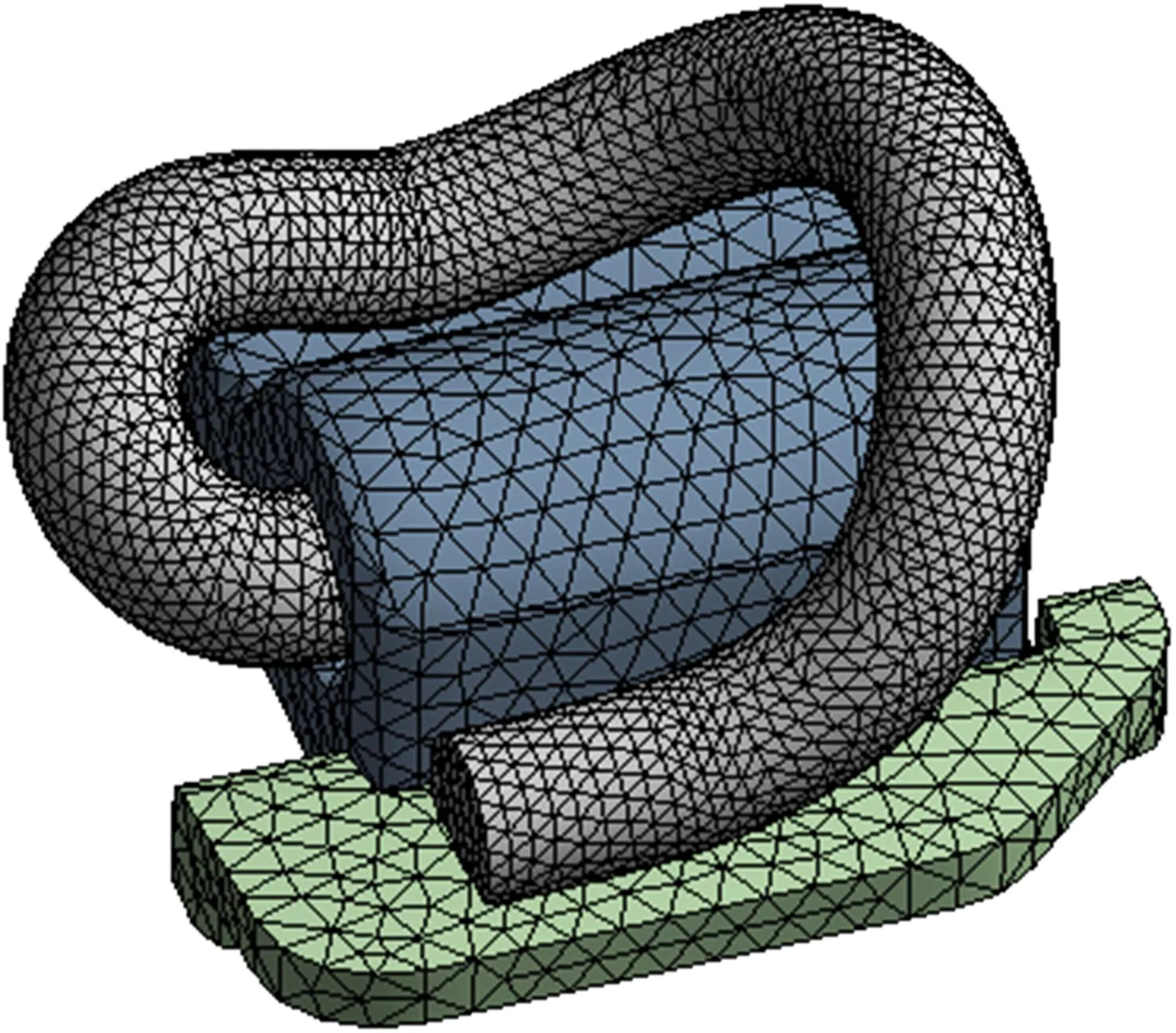
圖2 有限元模型Fig.2 Finite element model

鐵墊板底部采用固定約束以模擬真實邊界條件。通過在軌距擋塊的下表面施加向上的垂向位移荷載來模擬彈條的安裝過程，垂向位移13 mm為彈條的設計安裝彈程。應用非線性接觸理論準確模擬彈條與鐵墊板之間的復雜接觸狀態。接觸對類型選用摩擦接觸，具體接觸設置如表1所示。

表1 接觸設置Table 1 Contact settings

材料參數則根據實際扣件系統部件的材料進行設置。鐵墊板材料為QT450-10，軌距擋塊材料是玻纖增強聚酰胺66。彈條材料選用彈簧鋼，采用雙線性等強化模型來考慮彈條的彈塑性非線性屈服強度1 375 MPa，抗拉強度1 570 MPa。有限元模型各部件材料參數見表2。

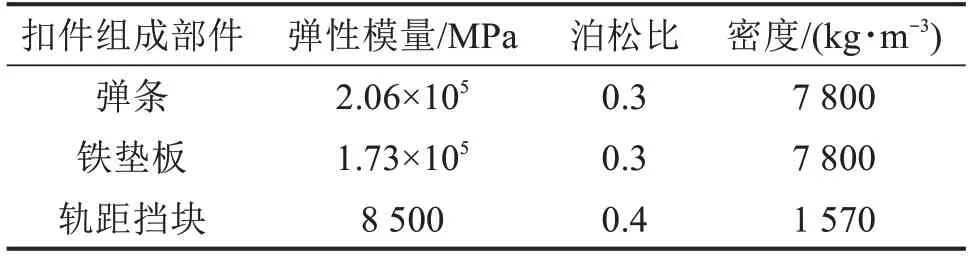
表2 材料參數Table 2 Material parameters

3.2 模型驗證

3.2.1 扣壓力驗證

取扣件安裝時彈條前拱小圓弧與鐵墊板支座之間的距離為9 mm，即彈條中肢插入深度為68 mm。圖3 是彈程和扣壓力關系圖。彈條扣壓力隨著彈程增大而線性增大，線性比值約為0.92 kN/mm。當彈條趾端變形達到安裝彈程13 mm 時，計算得到的常阻力彈條扣壓力為11.84 kN，滿足扣件設計初始扣壓力大于11 kN 的要求。

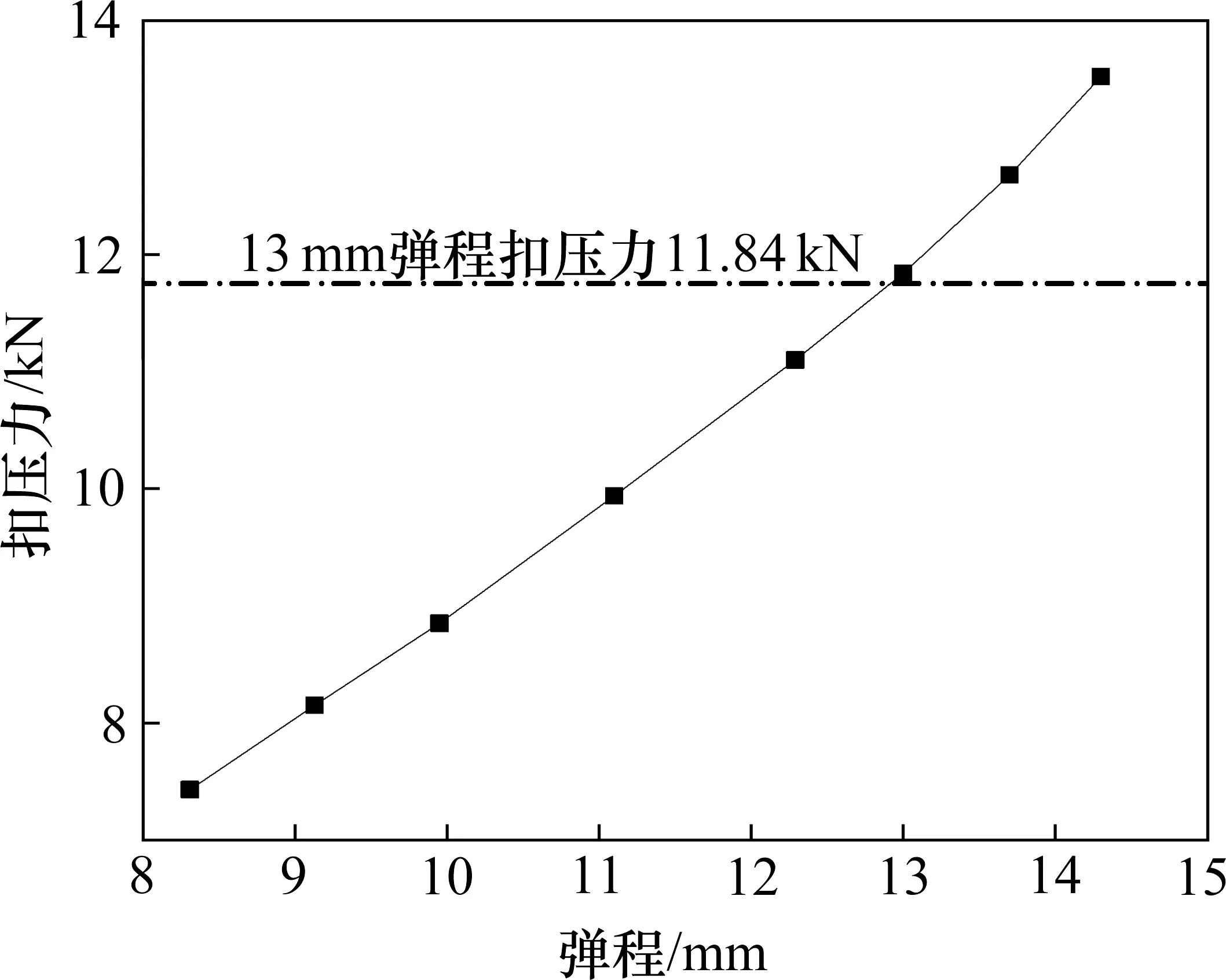
圖3 扣壓力與彈程的關系Fig.3 Relationship between the clip clamping force and clip displacement

3.2.2 Mises應力驗證

采用第四強度理論作為評價指標，彈條Mises等效應力如圖4所示。由計算結果可以看出，彈條正常安裝狀態下出現塑性區，彈條小圓弧內側區域處和大圓弧內側靠近鐵墊板區域處應力較大。最大等效應力為1 515.8 MPa，大于材料屈服強度(1 375 MPa)，小于材料破壞強度(1 570 MPa)。

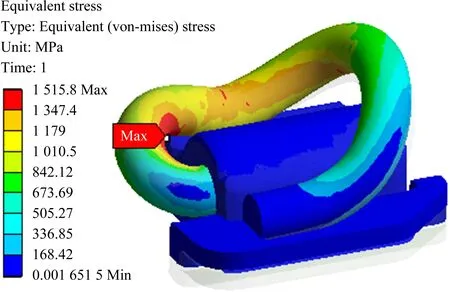
圖4 等效應力Fig.4 Equivalent stress

3.2.3 彈條自由狀態固有振動特性

為了得到彈條固有振動特性，本小節計算e 型彈條在自由狀態下0～2 000 Hz 范圍內彈條的固有模態頻率，各階模態如圖5所示，為了驗證彈條模型與固有頻率計算結果的正確性，將本文計算結果與既有文獻進行對比，具體振型描述與結果對比如表3所示。

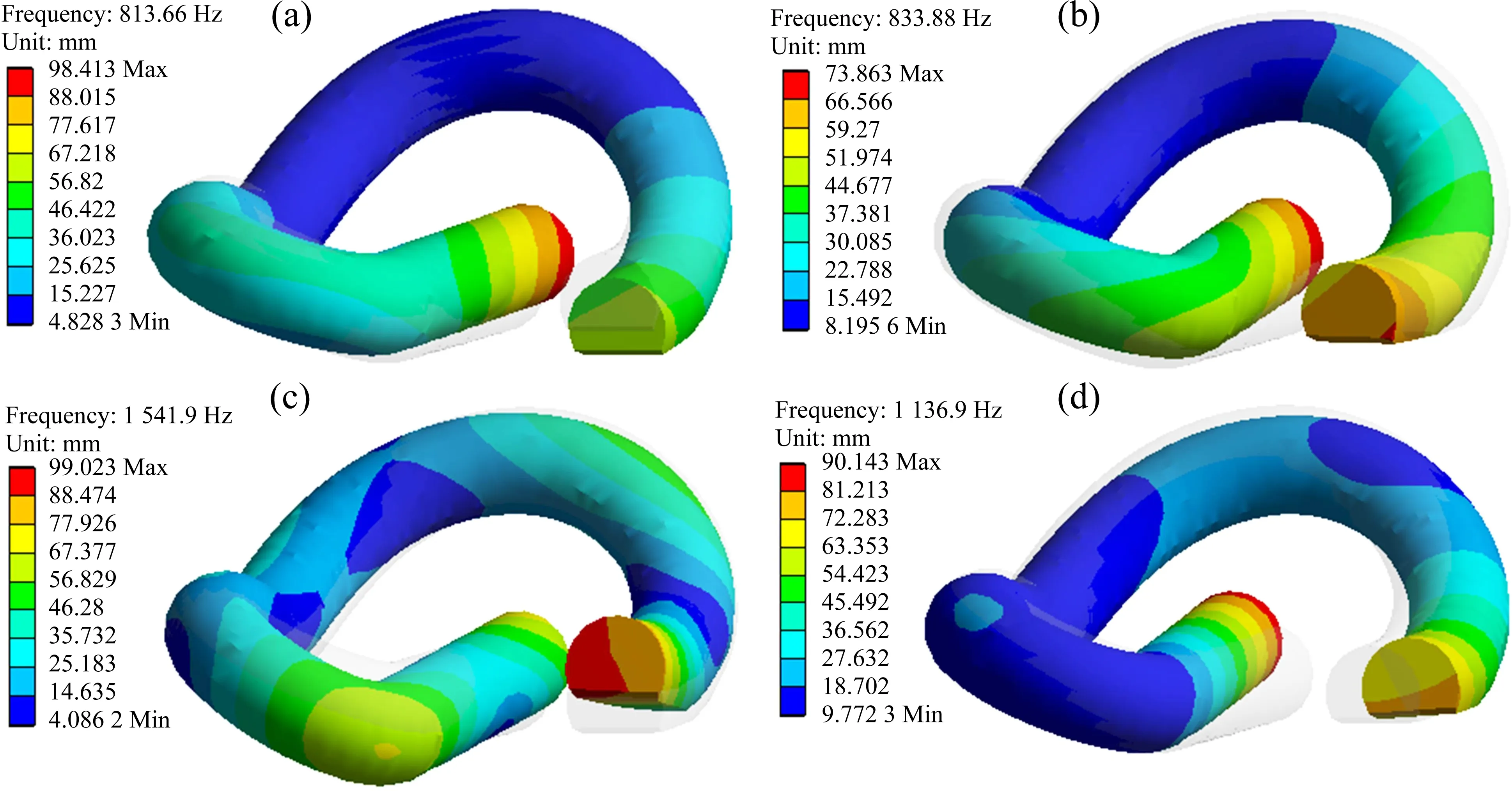
圖5 自由狀態彈條固有頻率Fig.5 Natural frequency of free spring

表3 振型描述Table 3 Modal description

4 e型彈條受載特征分析

e 型彈條斷裂失效問題與彈條受載條件下的應力狀態密切相關。為了分析研究e型彈條在真實受載條件下的斷裂危險點，首先計算正常服役條件下彈條應力狀態參數，在此基礎上，深入研究由鋼軌波磨引發的彈條共振條件下的彈條應力狀態。

4.1 彈條正常服役條件受載特征分析

圖6 是e 型常阻力彈條應力三軸度云圖。可以看出，在彈條正常安裝狀態下，彈條應力三軸度最大點為小圓弧內側與中肢連接處，彈條應力三軸度最大值約為0.65，表明此處是以拉為主的應力狀態，產生裂紋的幾率大，易引發彈條脆斷。e 型常阻力彈條應力軟性系數計算結果如圖7所示，彈條應力軟性系數最小點同樣出現在前拱小圓弧內側與中肢連接處，表明該位置應力狀態較硬，易發生脆性斷裂。

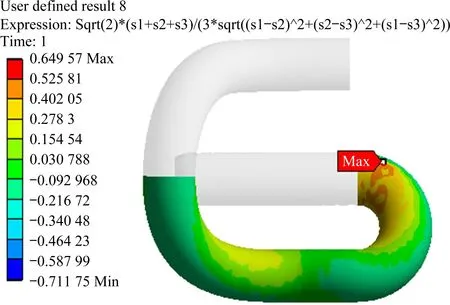
圖6 應力三軸度Fig.6 Stress triaxiality

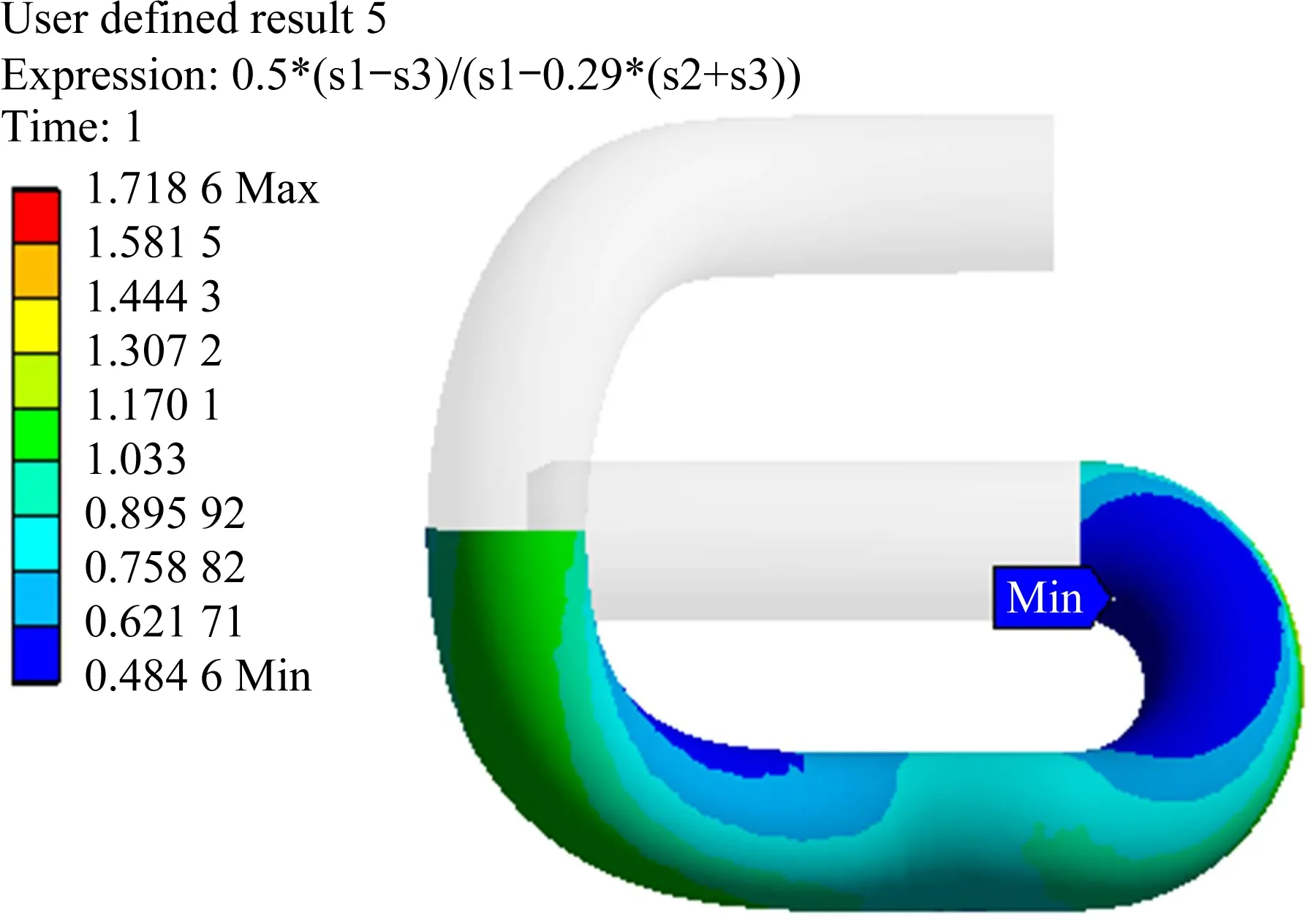
圖7 應力軟性系數Fig.7 Stress soft coefficient

通過圖8 羅德系數計算結果可以看出e 型彈條在安裝狀態下的受力狀態，小圓弧內側與中肢連接處羅德系數為-0.997 15，趨近于-1；外側羅德系數為0.995 9，趨近于1。這表明e 型彈條小圓弧內側為伸長類應變，外側為壓縮類應變。其中小圓弧內側與中肢連接處脆斷危險點處于三向受拉狀態，且為最大主拉應力點，對該位置裂紋的萌生與擴展產生不利影響，如圖9所示。

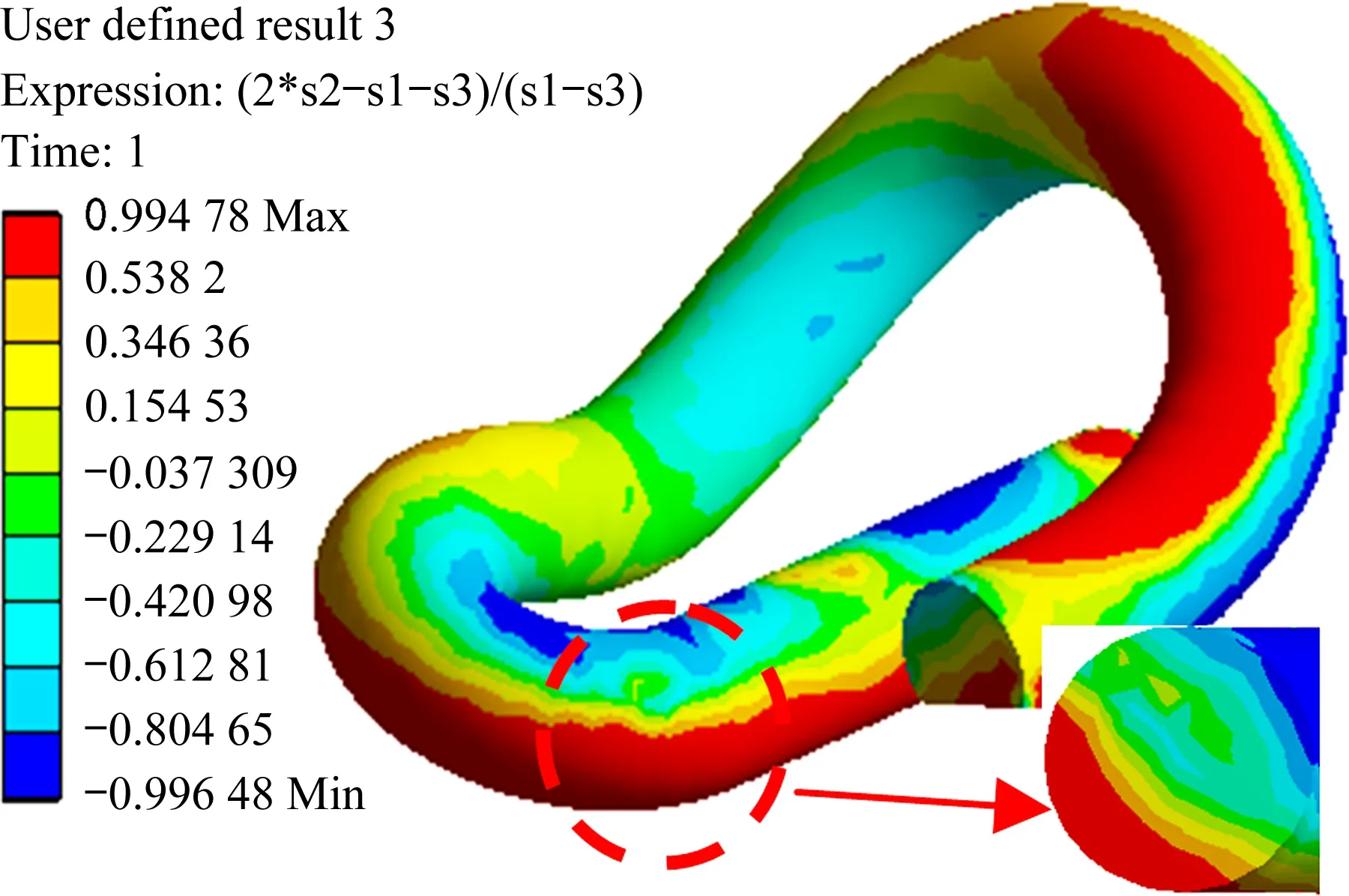
圖8 羅德系數Fig.8 Lode parameter

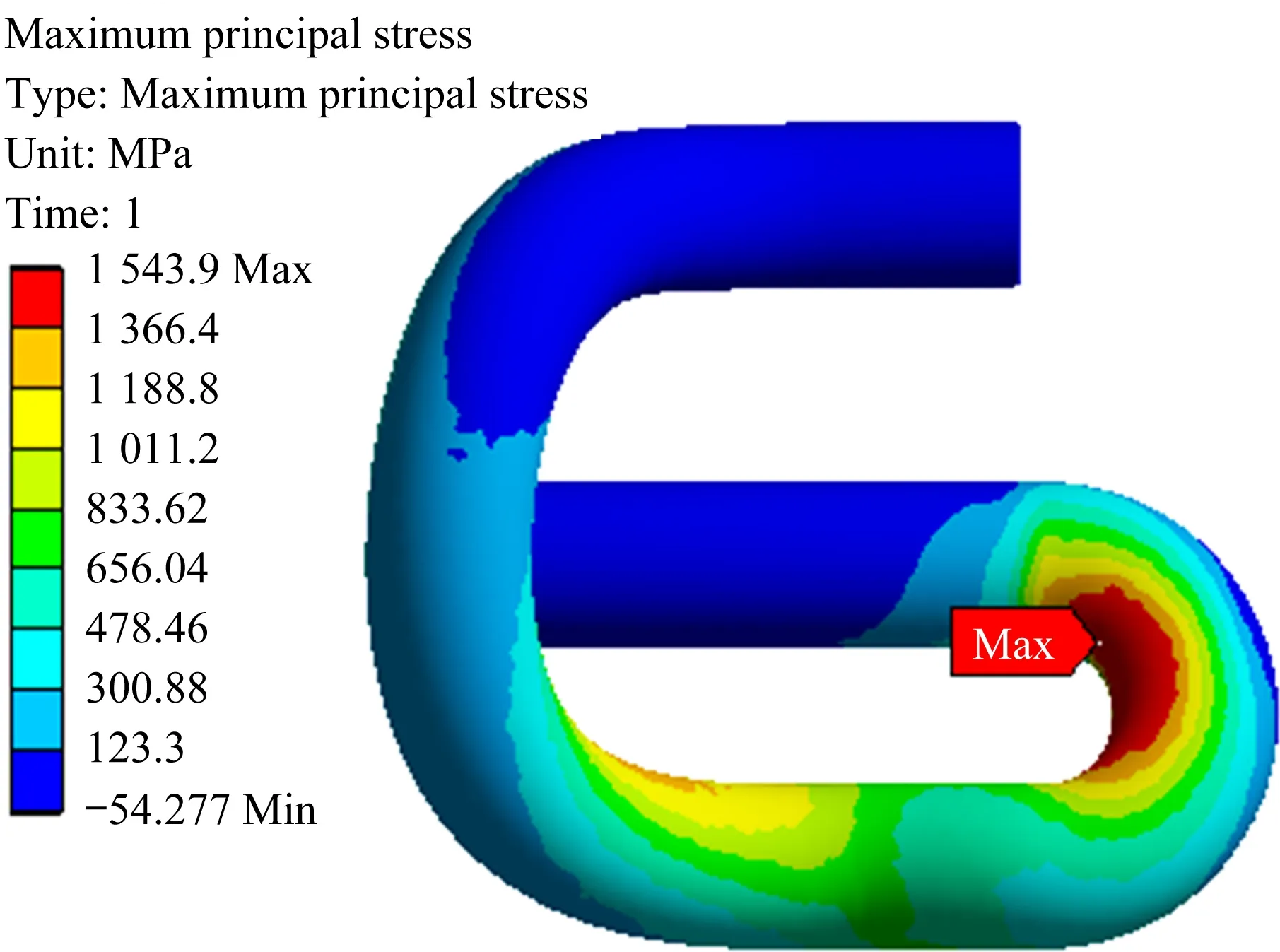
圖9 第1主拉應力Fig.9 First principal tensile stress

4.2 彈條共振條件下受載特征分析

鋼軌波磨通過頻率與彈條固有頻率一致引發彈條共振是造成彈條斷裂失效的重要外因。為了深入研究彈條在鋼軌波磨激振影響下的應力狀態，本節結合應力狀態參數概念，計算分析彈條在共振狀態下的斷裂危險位置。彈條在正常安裝條件下已經產生了趾端變形，此時彈條處于預應力狀態，在此基礎上計算得到彈條服役狀態下的固有頻率及其振動特性，如圖10 所示，對應振型描述見表4。

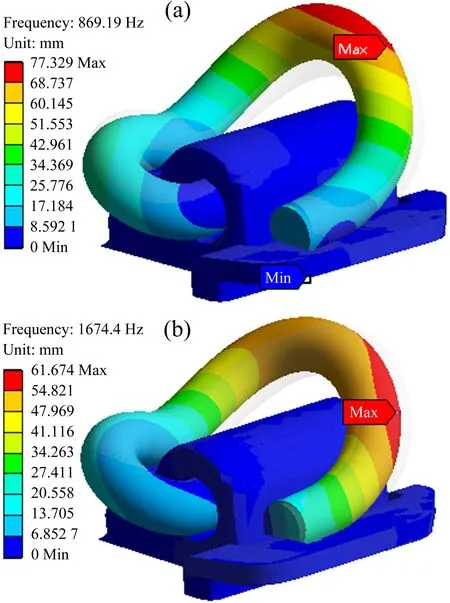
圖10 安裝狀態彈條固有頻率Fig.10 Natural frequency of clip in installation state

表4 振型描述Table 4 Modal description

DTIII型扣件系統e型彈條在服役條件下第1階固有頻率為869 Hz，與運營現場鋼軌波磨通過頻率范圍715～923 Hz 重合，彈條在鋼軌波磨高頻激勵條件下引發共振。彈條在共振狀態下的應力三軸度與應力軟性系數計算結果如圖11～12 所示。計算結果表明，彈條在第1階固有頻率共振時，彈條小圓弧與中肢連接處受到的三軸拉應力程度更高，更容易發生脆斷。彈條最大應力三軸度位置出現在彈條小圓弧與中肢連接處，最大應力三軸度為1.041 7，相比彈條在正常安裝狀態下增加63%。應力軟性系數最小值出現在彈條小圓弧與中肢連接處，最小應力軟性系數為0.459，相比彈條正常安裝狀態下減少5.4%。

圖11 應力三軸度Fig.11 Stress triaxiality

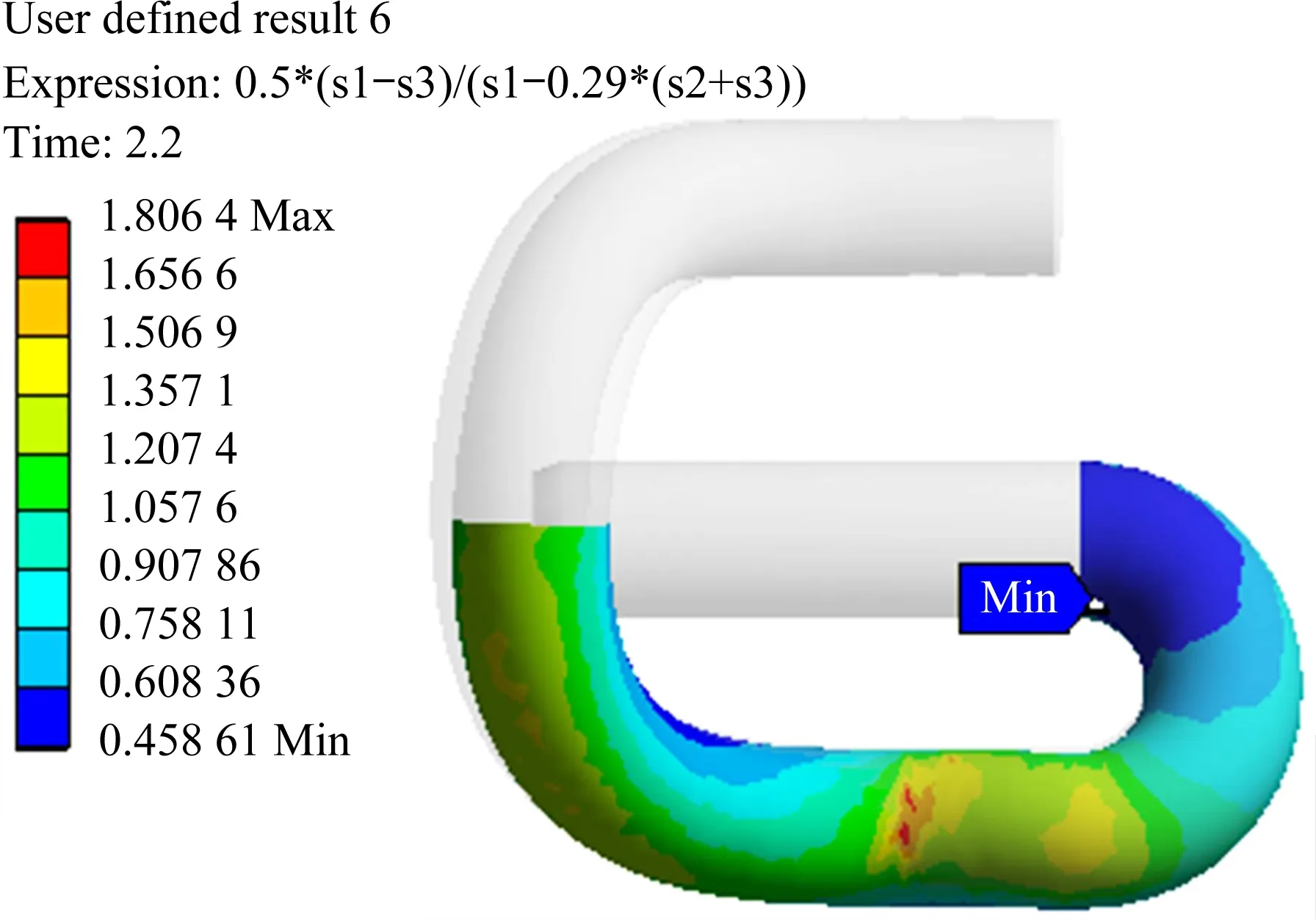
圖12 應力軟性系數Fig.12 Stress soft coefficient

為了進一步分析共振條件下彈條小圓弧與中肢連接處的受力狀態，圖13 給出了該位置處彈條橫斷面羅德參數計算結果與彈條最大主拉應力計算結果。可以看到，小圓弧內側羅德參數計算結果最小值約為-1，小圓弧外側羅德參數計算結果最大值約為1，這表明當彈條發生共振時，彈條小圓弧與中肢連接處橫斷面同樣是受到彎曲應力作用。彈條共振狀態下第1主拉應力最大值也出現在彈條小圓弧內側與中肢連接處，如圖14 所示，對于表面已經存在微裂紋的部件，裂紋尖端在拉應力場的作用下，其有效應力強度因子幅度必然增大，裂紋擴展速度非常快，進而導致彈條的突然脆斷，甚至飛濺打車，造成安全問題。

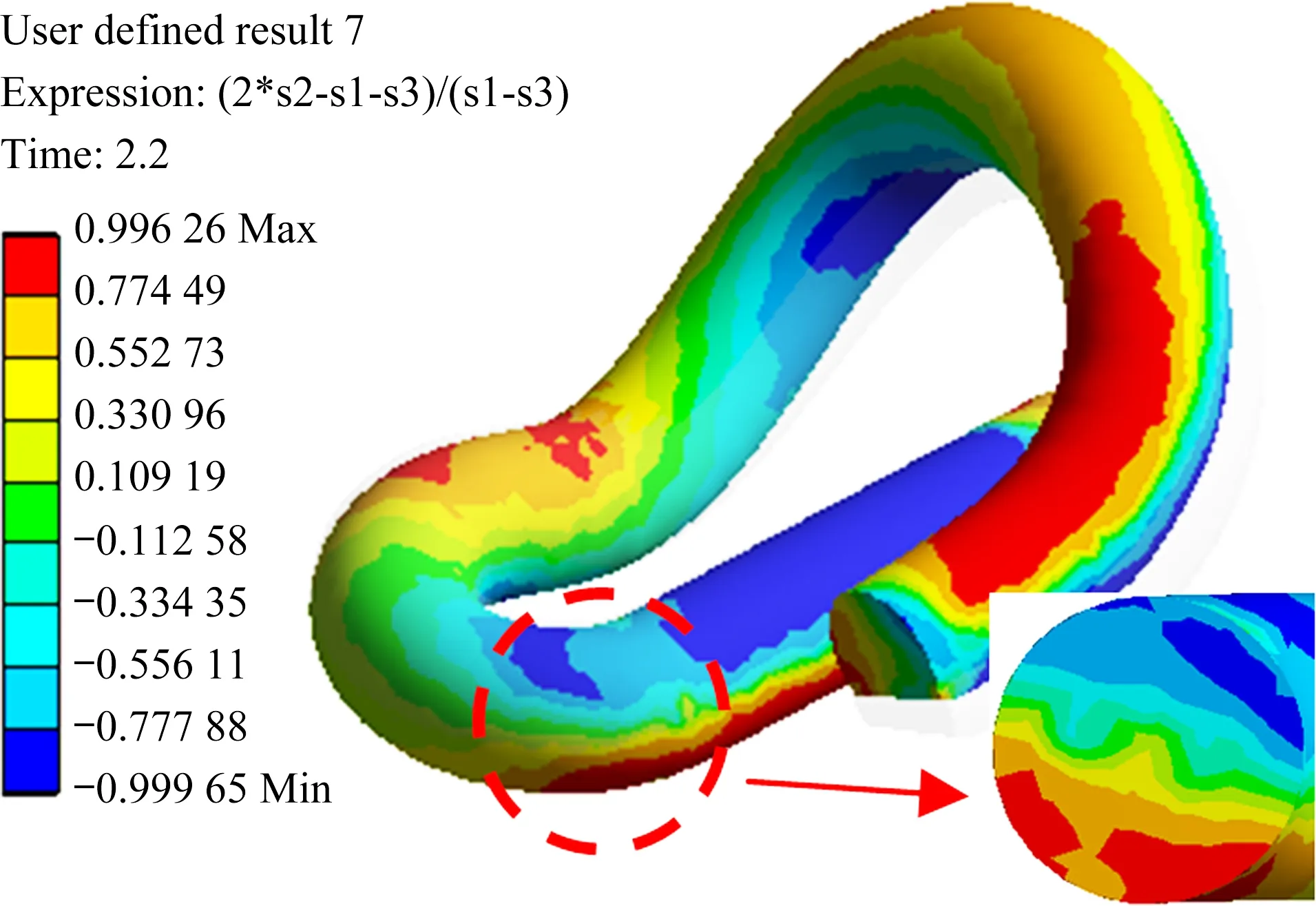
圖13 羅德系數Fig.13 Lode parameter

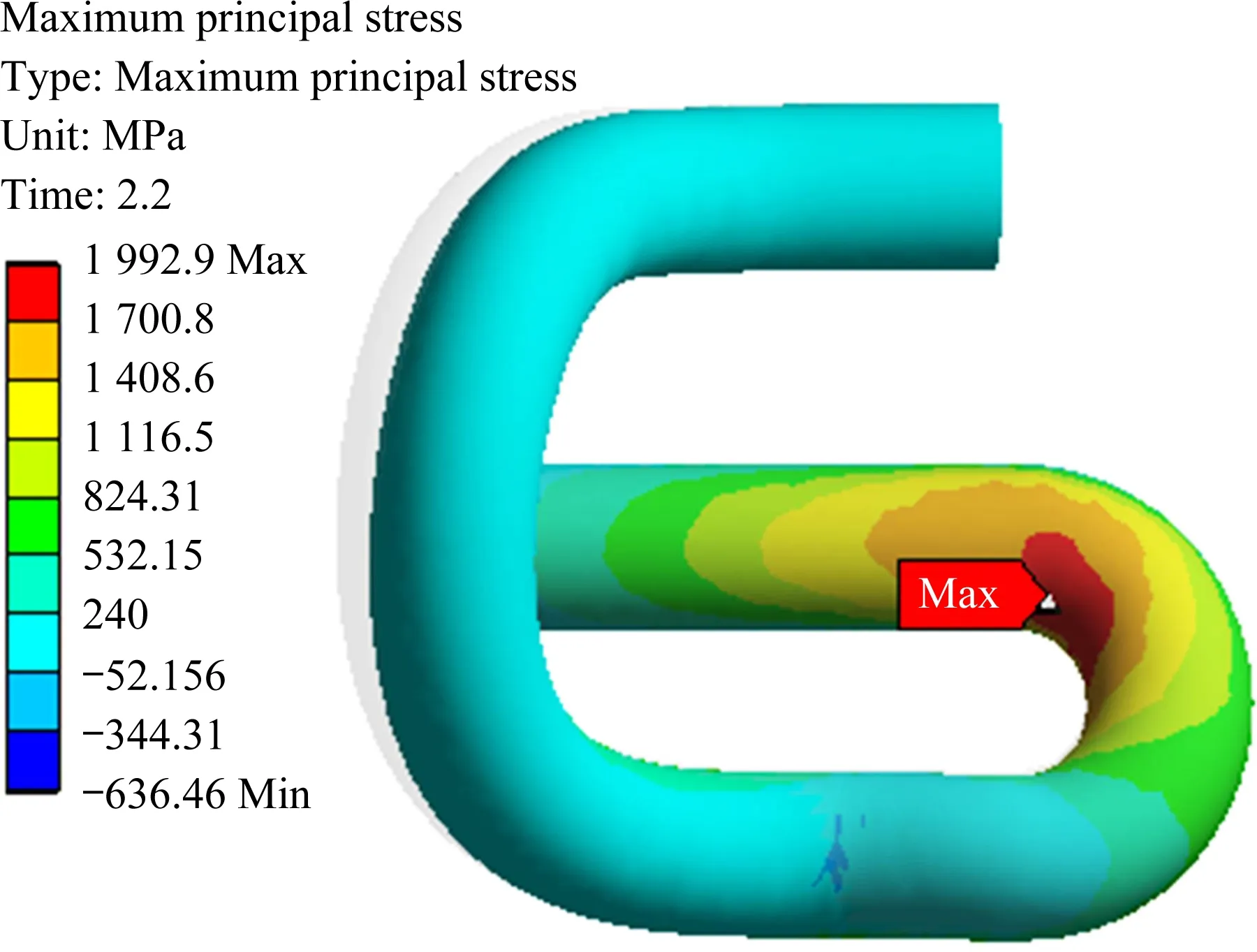
圖14 第1主拉應力Fig.14 First principal tensile stress

綜上所述，e 型彈條在正常安裝狀態與共振狀態下的斷裂危險位置均為彈條小圓弧與中肢連接處，本文計算結果與現場彈條斷裂位置高度吻合，如圖15 所示。尤其是在鋼軌波磨引發的共振條件下，彈條小圓弧內側與中肢連接處應力三軸度更大，應力軟性系數更小，彈條更易發生瞬間脆斷。

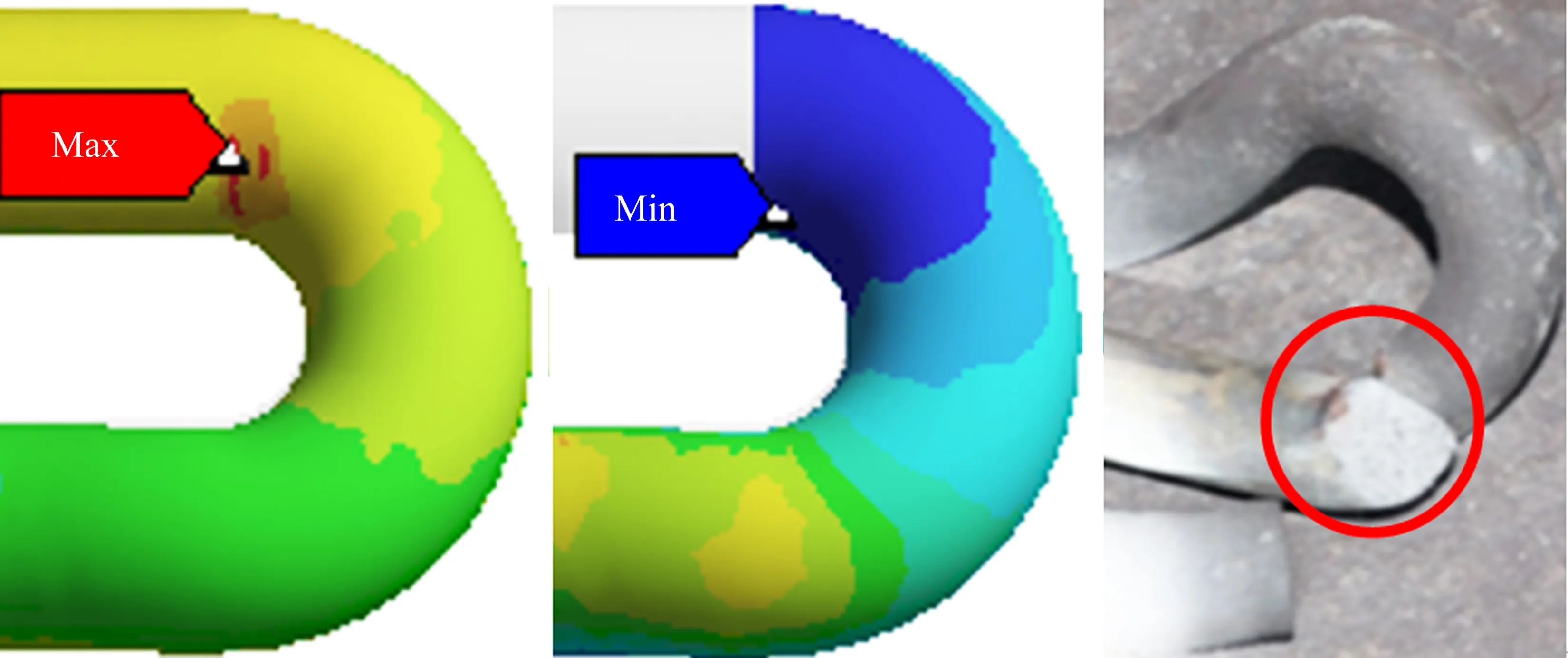
圖15 斷裂危險位置與現場實際破壞結果吻合Fig.15 Fracture risk points are consistent with the actual failure results

5 結論

1)e型彈條在安裝狀態下，彈程達到13 mm時，e 型彈條扣壓力為11.84 kN，彈條扣壓力滿足扣件使用條件，最大等效應力產生區域為小圓弧內側與彈條跟端連接處，最大等效應力為1 515.8 MPa。

2)e 型彈條在正常服役條件下應力三軸度最大值與應力軟性系數最小值均出現在前拱小圓弧內側與中肢連接處，表明該位置受到的三軸拉應力程度高，是彈條脆性斷裂的危險位置。通過提取e型彈條羅德系數分布云圖，可以看出，彈條小圓弧與中肢連接處橫斷面羅德系數內側約等于-1，產生伸長類應變，外側約等于1，產生壓縮類應變，橫斷面受到彎曲應力作用。提取該位置彈條主拉應力云圖可知小圓弧內側處于三向受拉狀態，并且為最大主拉應力點。

3)e 型彈條在第1 階固有頻率發生共振時，彈條應力三軸度最大值與應力軟性系數最小值出現在彈條小圓弧內側與中肢連接處。相比彈條在正常安裝狀態下，其最大應力三軸度增大60.3%，最小應力軟性系數減少5.4%，這表明e型彈條在共振狀態下彈條小圓弧內側與中肢連接處三軸拉應力程度加大，在波磨高頻激勵下更易發生脆性斷裂。由共振狀態下彈條羅德系數計算結果可知，彈條小圓弧與中肢連接處橫斷面同樣受到彎曲應力作用，第1主拉應力最大值也出現在該位置，在波磨引發的彈條劇烈振動條件下，彈條表面產生的微裂紋在拉應力場作用下會加速擴展，易于產生瞬間脆斷。