灰色系統預測模型在南京市物流需求預測中的應用*

□ 奚偉行,鄭 琰

(南京林業大學 汽車與交通工程學院，江蘇 南京 210037)

依托“一帶一路”經濟政策，我國的物流市場取得了一定規模的發展。平衡物流市場的供需對物流業的發展有著重要作用。通過查閱與瀏覽各種資料，發現國內對南京市物流需求的預測研究尚未有一個具體科學的預測方法，因此，本文通過建立灰色GM(1,1)模型，科學系統地分析南京市物流需求。

1 確立指標

要預測南京市物流需求，首先要明白南京市的物流市場主導需求。有很多指標可以用來研究物流需求，常見的有貨物運輸量、貨物運輸周轉量、倉儲量等，這些都是屬于事務量的范疇，還有一些價值體系的指標，常見的有物流活動產生的成本和收入等。由于這些指標難以統計和數據化，為了更好地對物流需求進行量化研究，本文通過貨物運輸量和貨物周轉量來表示南京市場流需求。

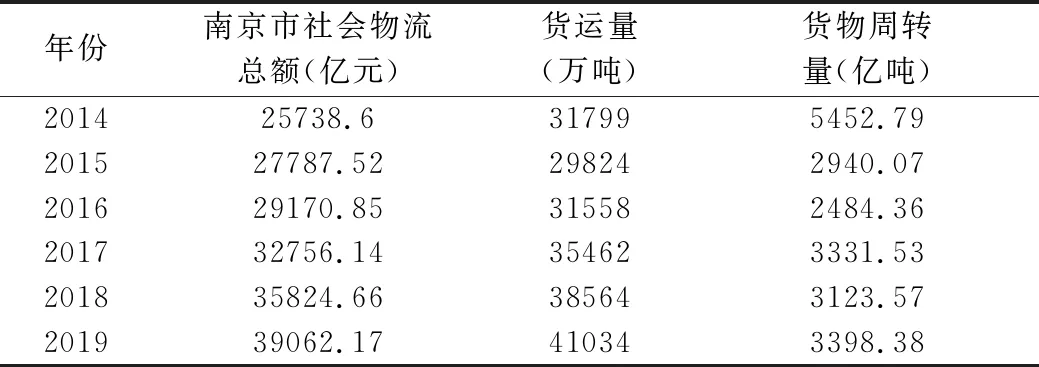
表1 2014-2019年南京市社會物流總額、貨物運輸量和貨物運輸周轉量

為了進一步確定物流需求的分析指標，本文基于能反應南京市物流市場需求的社會物流總額、貨物運輸量和貨物運輸周轉量進行關聯度分析，具體數據見表1。從表1中的各項數據整體來看，南京市物流需求呈現一定的增長態勢，但南京市物流需求的發展趨勢、需求變化與諸多因素有關，其中部分因素是未知且難以估計的，因此物流需求是一個“少數據、不完全信息”的灰色系統，用灰色關聯來進行分析無疑是一種有效的途徑[1]。下面就對貨運量、貨物周轉量和社會物流總額進行關聯分析。

1.1 設置參數

①以南京市社會物流總額為參考數列設

x1=(25738.6,27787.52,29170.85,32756.14,35824.66,39062.17)

②貨運量的數列為

x2=(31799,29824,31558,35426,38564,41034)

③貨物周轉量的數列為

x3=(5452.79，2940.07，2484.36，3331.53，3123.57，3398.38)

在建立的系統中，三個因素的實際意義并不相同，數據的量綱也不相同，貨運量單位為萬噸，貨物周轉量為億噸，不便于比較，因此，在進行灰色關聯度分析之前，要對表中數據進行無量綱化處理，本文采用了初始值法對三組數據進行處理[2]。

1.2 用初始值法處理數列x1，x2，x3

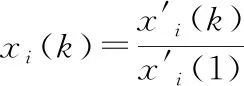
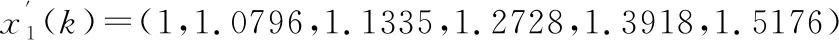
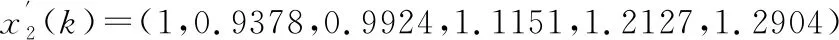
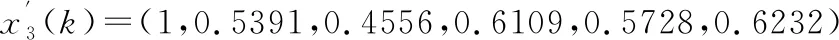
接著逐個計算每個被評價對象指標序列與參考序列對應元素的絕對差值，即

|X0(k)-Xi(k)|

(1)

得到的結果如表2所示[3]。

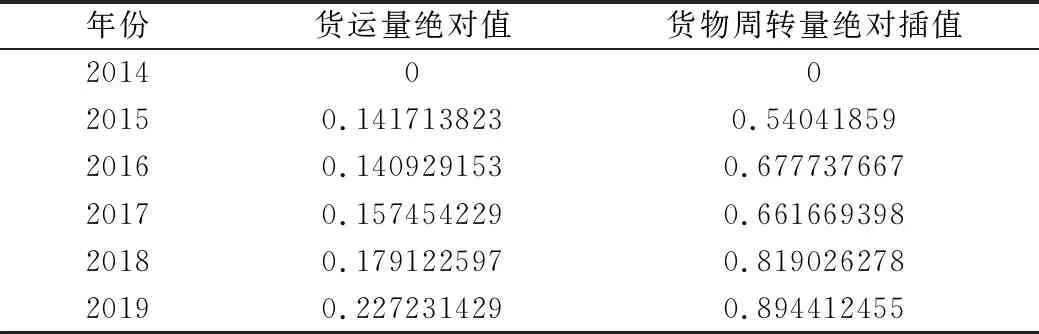
表2 2014-2019年南京市貨運量絕對值和貨物周轉量絕對值

1.3 計算關聯系數

關聯系數定義公式如下:

(2)

其中，ρ為分辨系數，0<ρ<1。若ρ越小，說明關聯系數間差異越大，區分能力越強。通常ρ取0.5。

最終計算關聯序，記為

(3)

通過計算得到南京市社會物流總額與貨運量的灰色關聯系數為R1=0.77,南京市社會物流總額與貨運周轉量的灰色關聯系數為R2=0.50,分析可得貨運量和貨運周轉量與南京市物流需求有比較好的關聯程度，并且貨運量的關聯程度大于貨運周轉量的關聯程度，因此本文選用貨運量為指標分析南京市物流需求。

2 貨運量的預測

2.1 貨運量

由上述分析可知，利用貨運量對南京市物流需求進行預測是具有一定準確性的，但單方面分析貨運量缺少條件因素影響，且對于南京市市場調控起不到指向作用，而對于南京市物流市場起到主要影響的是公路運輸，鐵路運輸，水路運輸，民航航空運輸。由于各種運輸的流量各不相同，分別預測再進行總量的相加會更加精準且全面。鐵路運輸、水路運輸、公路運輸、民航航空運輸具體數據如表3所示。

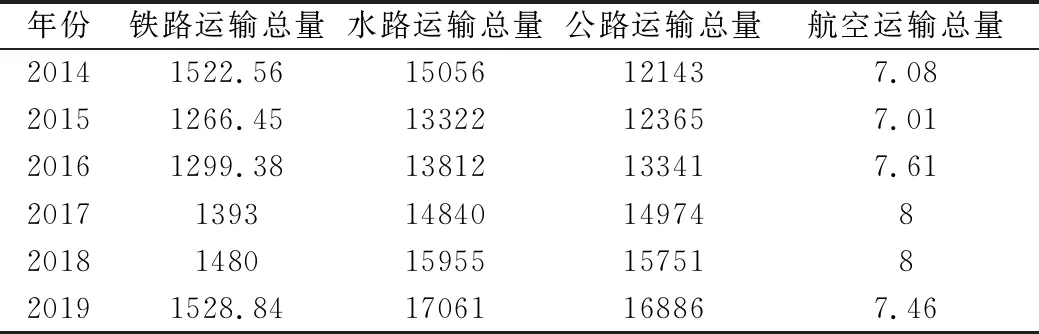
表3 2014-2019年南京市四種運輸方式的運輸總量

而在整個貨運量系統中，各種外界因素對其有很大的影響，系統信息的原始數據往往呈現離亂的情況，但灰色模型可以利用較少或模糊的數據進行處理，建立GM(1，1)一階微分方程，以揭示模糊系統內部的規律及發展變化。

2.2 建立GM(1,1)模型

①鐵路運輸總量數據序列：

②水路運輸總量數據序列：

③公路運輸總量數據序列：

④航空運輸總量數據序列：

對數列進行累加生成其AGO序列:

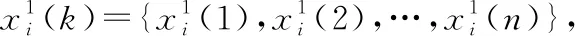
(4)

解得：

a1=-0.0506，u1=1147.067

a2=-0.0776，u2=11052.4

a3=-0.0646，u3=11726.7

a4=-0.01636，u4=7.1930

代入此方程可得時間響應模型：

(5)

可得：

①鐵路運輸貨物運輸量的響應方程為

X1=24165.92435e-0.05066(2014-t)-22643.36435

②公路運輸貨物運輸量的響應方程為

X2=154488.8493e-0.0776(2014-t)-142345.8493

③水路運輸貨物運輸量的響應方程為

X3=196538.9859e-0.0646(2014-t)-181482.9859

④民航航空運輸貨物運輸量的響應方程為

X4=446.8636822e-0.0164(2014-t)-439.7836822

算出累加量X(1)(t+1)，接著求出還原值：

X(0)(t+1)={X(1)(t+1)-X(0)(t)}

(6)

解得：

①鐵路運輸貨物量的灰色方程為

X1=(1-e0.05066)24165.92435e-0.05066(2014-t)

進行后驗差檢驗得c=0.139<0.35,小概率p=1符合一級精度。

②公路運輸貨物量的灰色方程為

X2=(1-e0.0077)154488.8493e-0.0776(2014-t)

進行后驗差檢驗得c=0.1196<0.35,小概率p=1符合一級精度。

③水路運輸貨物量的灰色方程為

X3=(1-e0.06462)196538.9859e-0.0646(2014-t)

進行后驗差檢驗得c=0.1083<0.35,小概率p=1符合一級精度。

④航空運輸貨物量的灰色方程為

X4=(1-e0.01636)154488.8493e-0.0776(2014-t)

因為量級為萬噸對其數據采取后驗差有一定誤差，對于這種數據我們采取了相對誤差檢驗，平均相對誤差小于5%，經過計算可得，灰色GM(1，1)模型對四種運輸量預測都有較好的擬合度，且四種運輸量均呈上升趨勢，與實際經濟發展情況相符，所以該預測還是較為成功的。我們將四個運輸量的8年后預測數據相加，得到南京市貨物運輸總量，如表4所示。

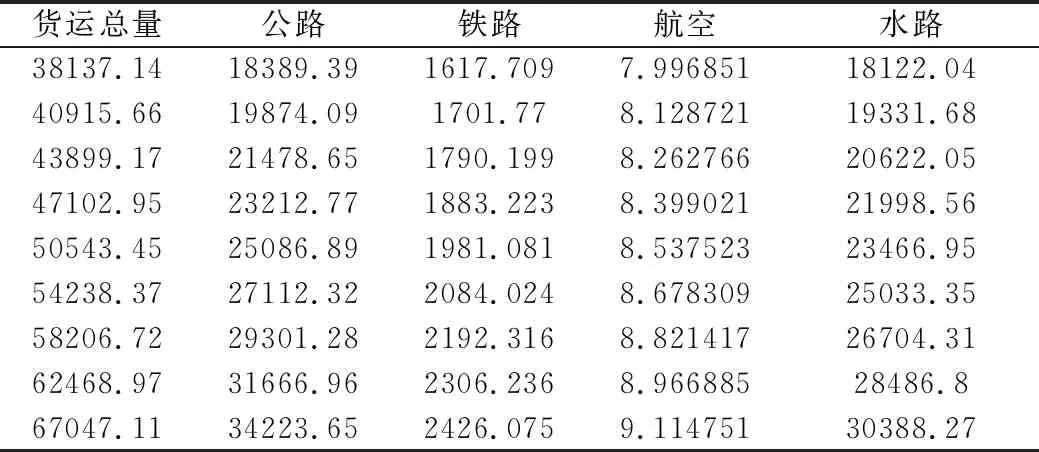
表4 2020-2028各年份數據預測數值

由表4我們可知，南京市貨運總量發展良好，且南京市物流市場需求呈增長趨勢，因此物流企業可以適當地擴大發展規模，以達到市場供需平衡，避免需求過大，對企業造成其他方面的損失。為了更有利于政府調控南京市物流市場，我們建立多元回歸模型，抓住對整體物流需求增長起促進作用的正相關因素，積極發揮企業和政府的生產力，投入資金和人力來發展關鍵因素，進一步擴大物流業規模。

2.3 多元回歸模型的建立

為了更好把握南京市物流市場的主導因素，本文通過四個變量的預測數據與貨運量建立數學上的線性關系，建立影響社會物流量變化的自變量與因變量之間的相關關系模型。本文將貨運總量設為因變量，將公路運輸量、鐵路運輸量、航空運輸量、水路運輸量設為自變量，建立多元回歸方程。

設公路運輸量、鐵路運輸量、航空運輸量、水路運輸量為Xi，i=1,2,3,4。

y=a1x1+a2x2+a3x3+a4x4

(7)

依據表4數據計算多元回歸方程得：

y=0.945x1+0.028x2+1.137x3+0.004x4

(8)

從該方程我們可以看出，各個因素都呈正相關關系，各個運輸行業都對物流需求起積極作用，水路和公路運輸量占貨物運輸總量比重較大，且影響因子很大，符合南京市公路和港口經濟發展規模的實際意義，參考意義較大，政府可擴大公路和水路的物流市場，也可全面發展其他行業的運輸產業。

3 結論與建議

首先我們通過灰色關聯度確立了貨運量為南京市物流需求的指標，關聯度較大，也符合實際意義，接著我們分別分析了公路運輸貨運量、鐵路運輸貨運量、水路運輸貨運量和民航航空運輸量四者預測值總和，求得南京市貨運總量，發現南京市貨運量呈現增長趨勢，符合經濟發展趨勢，且通過建立多元回歸模型，計算出四者作為自變量與南京市物流呈正相關，且公路和水路影響程度較大。為了利于南京市政府宏觀調控物流市場，本文提出如下幾點發展建議。

①由預測數據可知，公路運輸量在未來幾年增長趨勢較明顯，說明貨運量的發展規模占主導作用，也表明了第三方物流企業發展速度較快，第三方物流的主要市場為公路運輸，南京市政府可適當提出相關政策發展第三方物流，促進公路運輸的發展。

②南京處于長三角經濟帶，要充分發揮南京港的天然優勢，依托長江發展水運，協調各個區域港口，如江陰港、上海港等規模較大的港口，充分發揮水運貨運量大等特點。

③加強各區域物流樞紐的合作，產生物流企業聚集效應，加強物流企業之間的溝通，以節約物流企業成本，使物流業主要的運輸企業發揮其在不同運輸方式的優勢，以長補短，調節物流市場。