一種研究死區非線性對系統頻率特性影響的圖解方法

劉 鵬，李懷兵，楊超凡，陳 婷，劉 凱

(北京精密機電控制設備研究所， 北京 100076)

死區非線性廣泛存在于控制系統[1-3]，在電動伺服系統中也經常用死區非線性來描述傳動間隙。死區非線性會影響控制系統動態性能和穩態精度，并且會產生極限環振蕩，影響系統穩定性[4-7]。目前已有較多文獻研究死區非線性對系統穩定性的影響[8-11]，但研究系統性能的影響因素的文獻較少。綜合運用描述函數法，等M圓、等N圓，以電動舵機為研究對象，通過一種圖解方法分析了死區非線性對控制系統閉環頻率特性的影響。

1 電動伺服系統

1.1 電動伺服系統傳動機構

圖1為典型的驅動飛行器舵片的電動舵機結構示意圖。其運動傳遞過程為：電機轉動通過齒輪副傳遞給滾珠絲杠副，絲杠螺母上安裝有線位移傳感器，將位置信號反饋給控制器，形成閉環控制。此外，絲杠螺母通過銷軸與搖臂和連桿連接，通過舵軸最終驅動舵片偏轉，絲杠螺母到舵片的傳遞過程沒有進入閉環回路，屬于開環控制，但是可以通過負載效應影響到閉環性能。

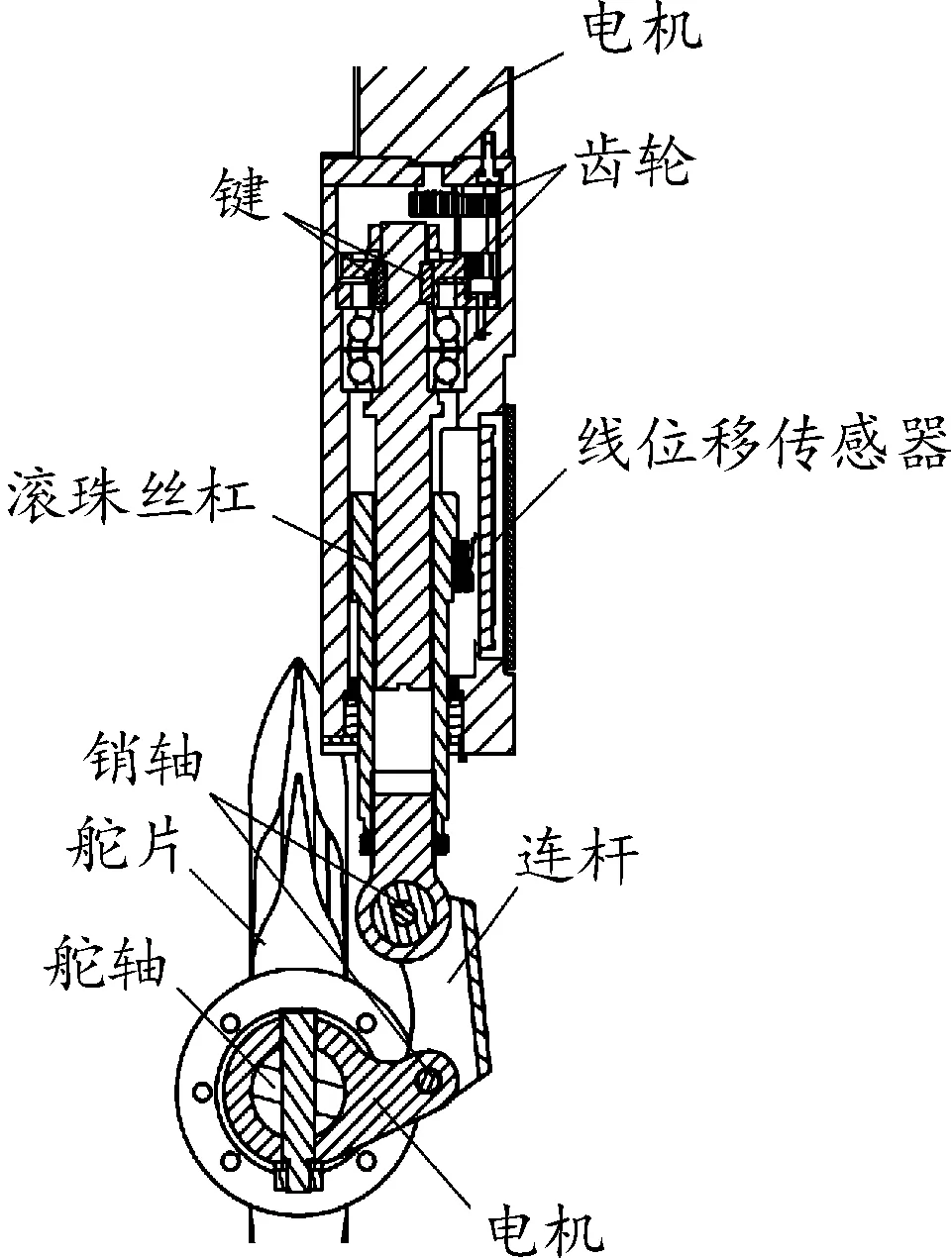
圖1 電動舵機結構示意圖

在閉環回路中，電機一般通過圓柱銷或平鍵與主動齒輪連接，從動齒輪一般通過平鍵與滾珠絲杠連接，圓柱銷一般為過盈配合，平鍵一般采用雙鍵，可有效消除間隙。滾珠絲杠副一般通過增大鋼球消除間隙。所以在閉環回路內部，傳動間隙主要存在于齒輪副中。

在閉環回路外部，由于搖臂和連桿必須要相對轉動，因此，銷軸與銷軸孔的配合需要有一定間隙，此傳動間隙屬于閉環外間隙，在本文中稱為負載間隙。

1.2 電動伺服系統中傳動間隙的數學模型

圖2為用死區模型模擬間隙的齒輪傳動數學模型，在該模型中，死區寬度代表齒輪間隙值，模型中各參數含義如下：K剛度為齒輪嚙合剛度；i齒輪為齒輪減速比；JT為從動部分轉動慣量；fT為從動部分粘性阻尼系數；KT為負載力矩系數。

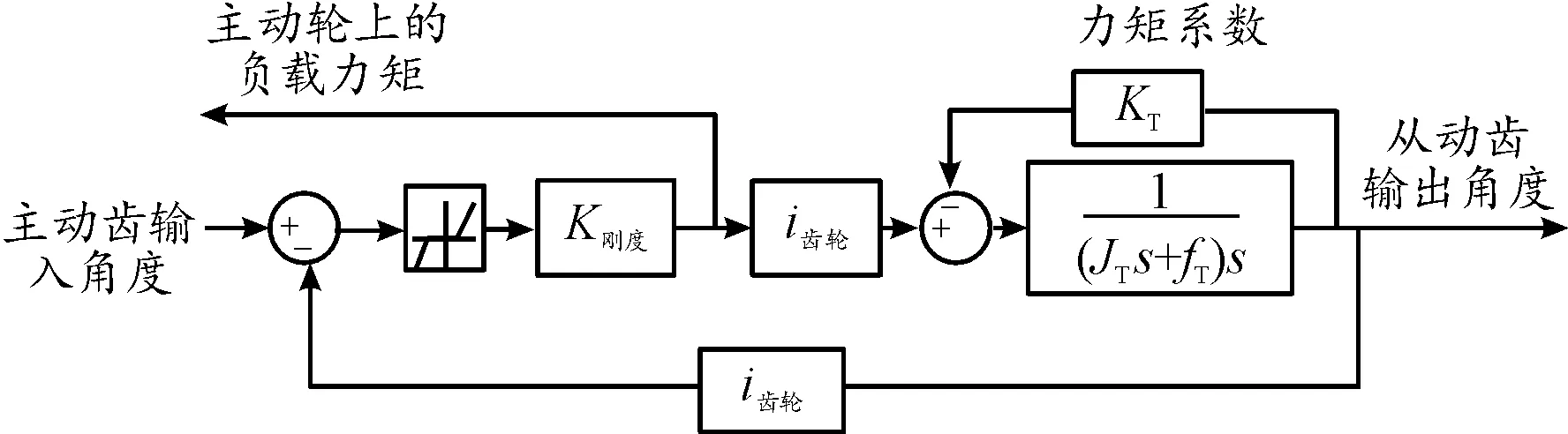
圖2 齒輪傳動數學模型示意圖

圖3為用死區模型模擬間隙的連桿搖臂機構數學模型，在該模型中，輸入為電動舵機中絲杠螺母的伸縮量，輸出為舵片轉動角度，死區寬度代表銷軸與銷孔的間隙值，模型中各參數含義如下：KW為負載等效剛度；L力臂為搖臂力臂長度；JW為負載轉動慣量；fW為負載粘性力矩系數；K弧角為弧度角度轉化系數；K角線=L力臂/K弧角，將舵片轉角折合為絲杠螺母伸縮量系數；i為負載到電機的總減速比；KT為負載力矩系數。

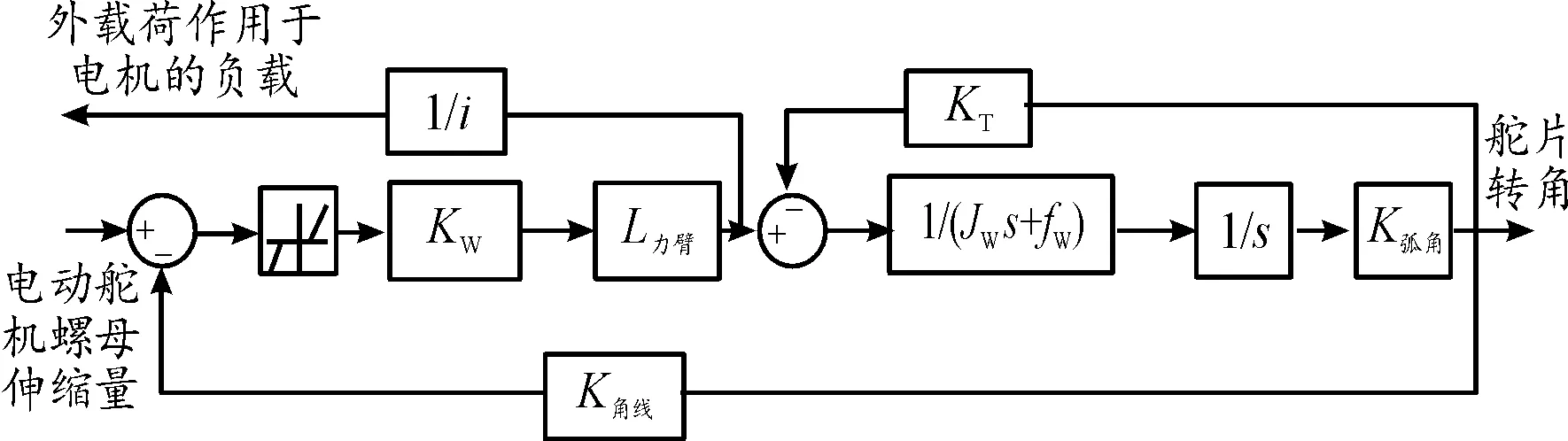
圖3 連桿搖臂機構數學模型示意圖

將上述模型放到系統中，可得到考慮間隙的電動舵機伺服系統數學模型。

2 負載間隙對伺服系統閉環頻率特性的影響

只考慮負載間隙，不考慮閉環回路內的齒輪間隙，可得伺服系統模型，如圖4所示。模型中參數定義如下：P為比例系數；U為供電電壓；L為電機等效電感；R為電機等效電阻；Cm為電機力矩系數；Ce為反電動勢系數；fd為電機粘性力矩系數；Jd為電機的轉動慣量；i齒輪為齒輪的減速比；i絲杠為絲杠的減速比；K線角為作動桿伸出長度轉化為舵軸轉角的轉化關系。

按圖4模型進行仿真，以控制角度為輸入，輸入信號為r=1°sin(ωt)，舵片轉角為輸出，負載間隙值分別取0、0.05、0.1 mm，求解不同頻率響應的幅值和相位[12]，系統的幅頻特性及相頻特性如圖5所示。典型頻率下的幅頻數值見表1，相頻數值見表2。

圖4 考慮負載間隙的伺服系統模型示意圖

表1 幅頻特性

表2 相頻特性

從仿真結果看，隨著間隙的增大，在低頻處，幅值會衰減，但隨著頻率的升高，幅值反而會增加；隨著間隙的增大，相位變化不大。為何會出現這種情況，傳動間隙是如何對系統頻率特性造成影響的，可用圖5中的圖解方法進行探究。

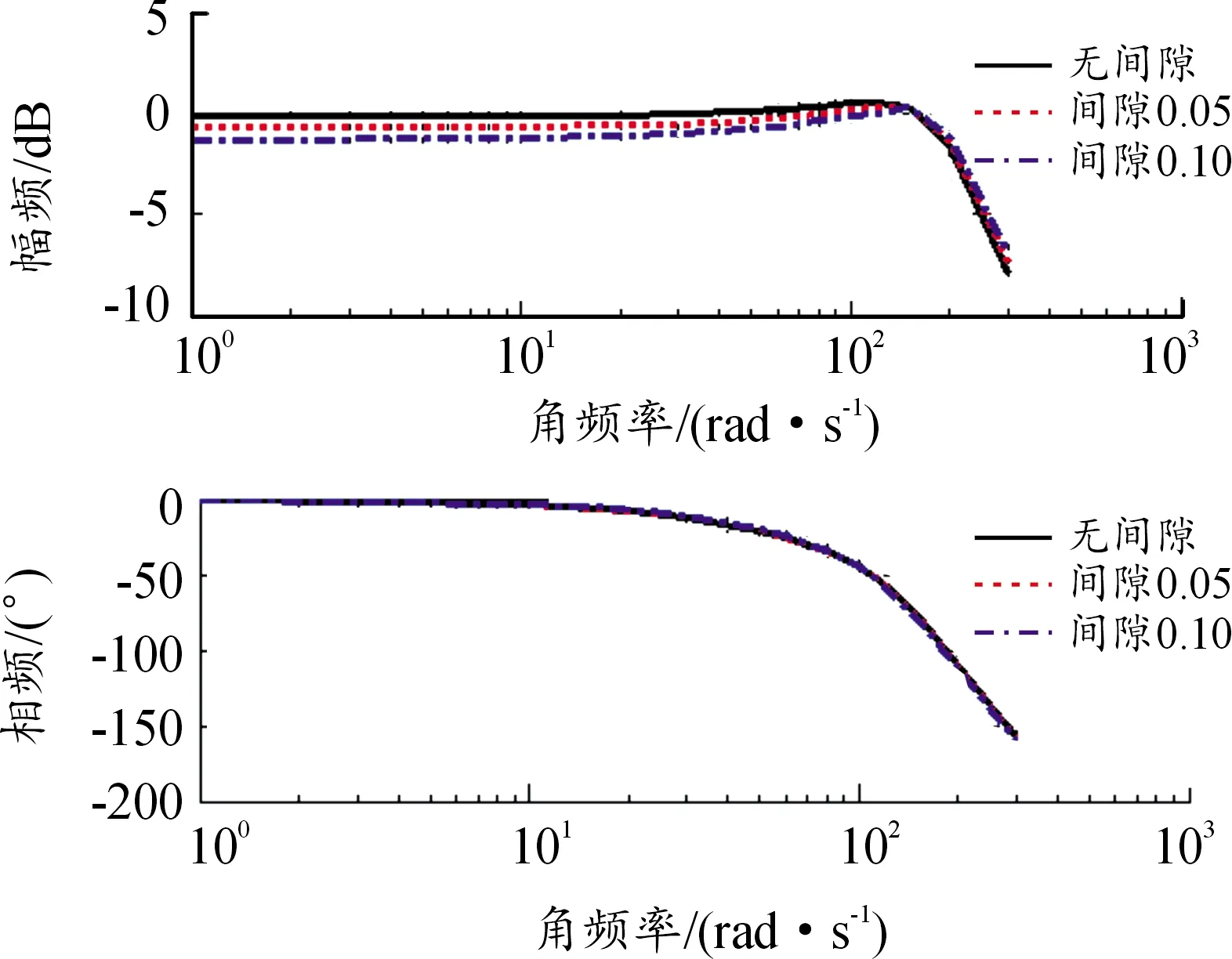
圖5 不同負載間隙下系統閉環bode圖

按描述函數的理論[13-15]，非線性環節可以看成一個變增益的環節，其增益值與輸入幅值有關。按如下思路分析負載間隙對頻率特性的影響：① 對系統等效變換以便于分析，為能通過開環頻率特性得出閉環頻率特性，需將研究對象轉化為單位負反饋系統；② 計算系統在不同頻率下非線性環節等效的增益值N(A)；③ 將不同的N(A)代入單位負反饋系統的開環傳遞函數，得到含間隙的開環傳遞函數；④ 通過等M圓可以在單位負反饋系統開環幅相曲線上直觀地讀出間隙對系統閉環幅值特性的影響，通過等N圓可以直觀地讀出間隙對系統閉環相位特性的影響。

按上述理論進行分析，先對模型進行等效變換，將死區環節替換為一個變增益環節N(A)，由于負載部分與舵機部分通過力的傳遞而產生耦合關系，通過移動比較點和引出點，將負載部分和舵機部分解除耦合關系，如圖6所示。從圖中可以看出，對于舵機部分而言，N(A)只會影響其內部回路的反饋系數，因此，認為N(A)對舵機部分頻率特性影響較小。

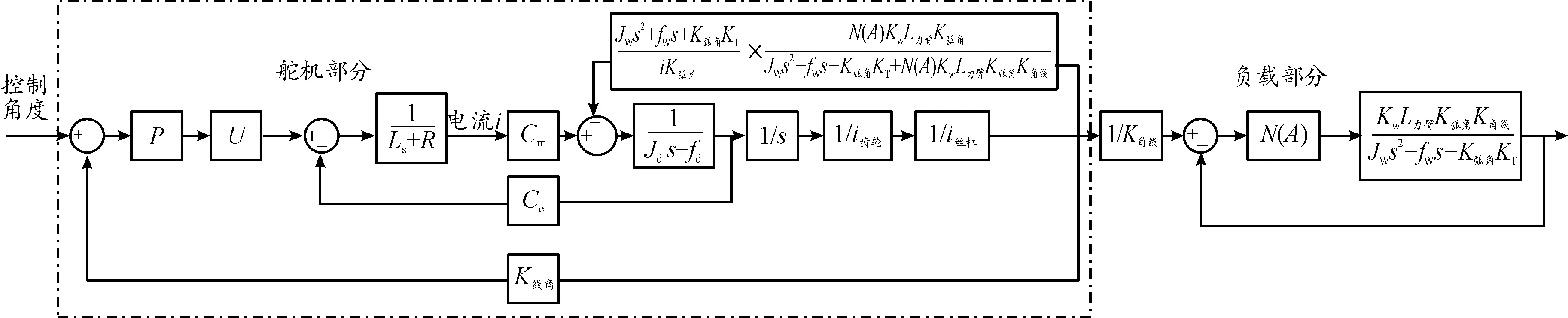
圖6 模型等效變換結果

圖6模型等效變換結果用圖4所示模型進行仿真，以控制角度為輸入，線位移傳感器作為輸出，分別計算不同間隙的線位移輸出。從圖7中可以看出，不同間隙值下，線位移幅頻和相頻曲線基本重合。因此，可以只研究負載部分。

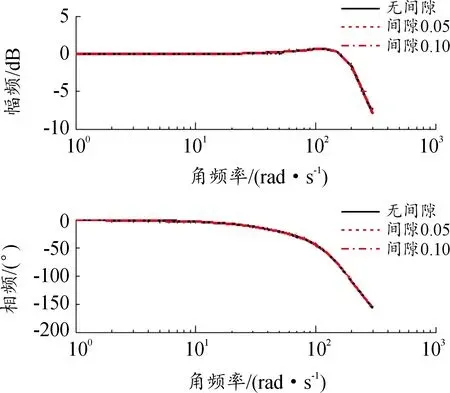
圖7 不同負載間隙下系統線位移傳感器輸出bode曲線

為使用等M圓、等N圓進行研究，將負載部分等效變換為單位負反饋系統，如圖6所示。由于單位負反饋回路與其他回路是串聯關系，間隙環節只對單位負反饋回路有影響，所以，間隙對系統的影響可以簡化為間隙對單位負反饋回路的影響。

2.1 單位負反饋回路開環幅相曲線

如圖6所示，單位負反饋回路的開環傳遞函數為

(1)

死區環節的描述函數為：

A≥Δ

式中：A為輸入信號幅值；2Δ為死區寬度。從公式中可以看出，N(A)不含虛部且值恒小于1。

計算死區環節的等效增益N(A)的取值有2種方法：① 計算處死區環節的輸入值，然后代入描述函數公式得到N(A)；② 分別對死區輸出和輸入信號進行數字傅立葉變換，幅值相除，即可得N(A)值。現采用第2種方法。表3為不同間隙、不同頻率下，計算出的N(A)值。

表3 不同頻率、不同間隙下的N(A)值

當N(A)=1時，得到無間隙時的開環幅相特性及開環幅相特性曲線。將不同間隙之下，不同頻率處的N(A)值代入式(1)，得到其開環幅相特性，畫在復平面上就可以得到不同間隙下的開環幅相曲線，如圖8所示。

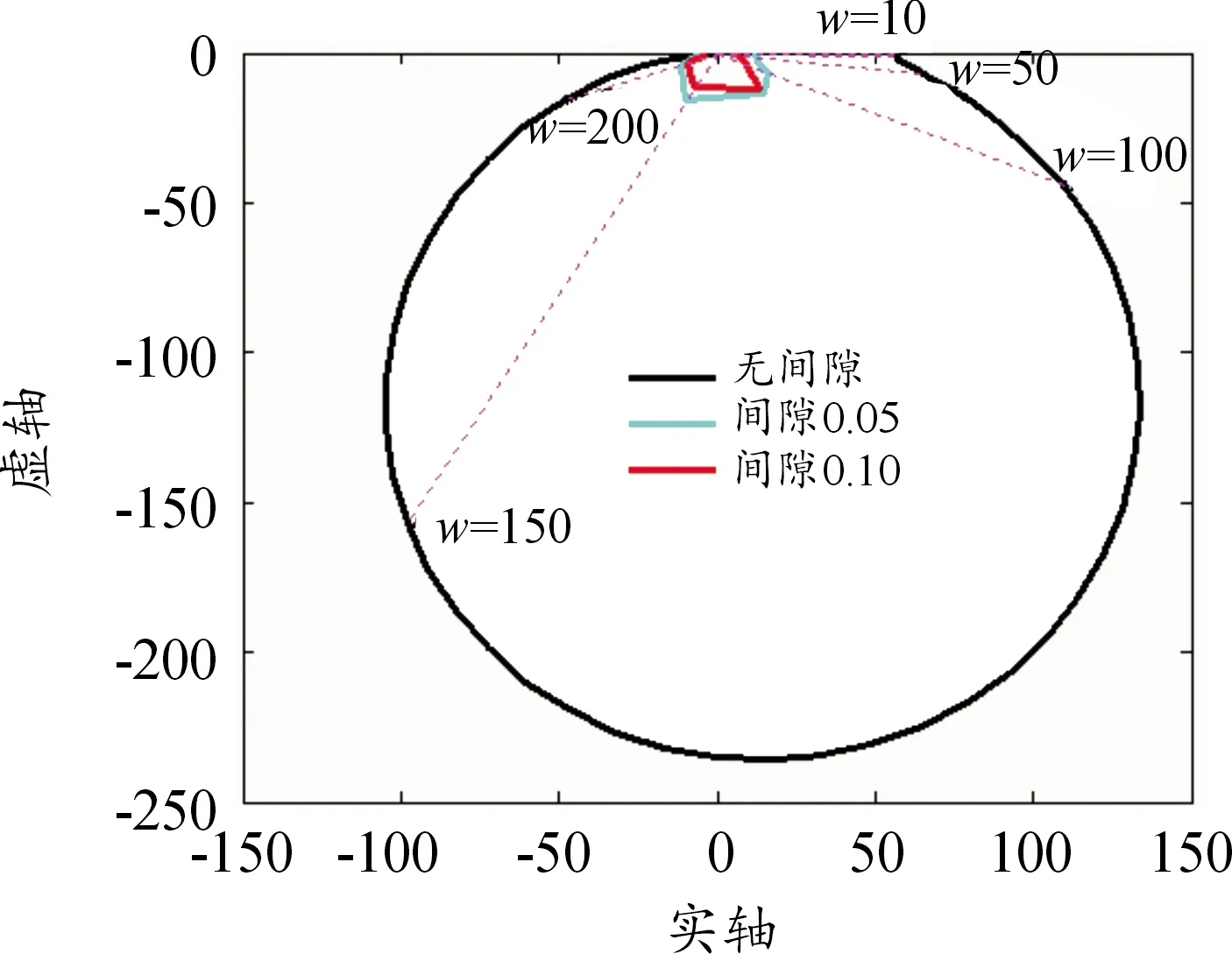
圖8 不同間隙值下的開環幅相曲線

由于將N(A)視為一個小于1的純比例環節，不影響相位，因此將各頻率下幅相特性在復平面上的點與原點連接起來形成一條直線，當N(A)變化時，同一頻率的幅相特性將在該直線上移動，死區環節的效果是使各頻率對應的點在復平面上沿直線向原點移動。

2.2 系統閉環幅值特性

對于單位負反饋系統，通過等M圓可以直接在開環幅相曲線上讀出閉環幅值特性。等M圓軌跡是一簇圓公式：

(2)

式中，M為系統閉環幅值特性。當M=1(0 dB)時，它是通過(-1/2，0j)點、平行于虛軸的一條直線。

當M>1(0 dB)時，隨著M值的增大，等M圓半徑越來越小，最后收斂于(-1，0j)點，且這些圓均在M=1(0 dB)直線的左側；

當M<1(0 dB)時，隨著M值的減小，等M圓的直徑越來越小，最后收斂于原點，且這些圓均在M=1(0 dB)直線的右側。

將等M圓畫在上一節的開環幅相曲線中，如圖9所示，從圖中可以直接讀出不同間隙下，單位負反饋環節各頻點的閉環幅值。由于w=1～100 rad/s開環幅相曲線位于等M圓0 dB線右側，因此隨著N(A)值的變小，閉環幅值也變小；w=150～200 rad/s開環幅相曲線位于等M圓0 dB線左側，隨著N(A)值的變小，閉環幅值增大，這與圖5及表1所示的仿真結果是一致的。

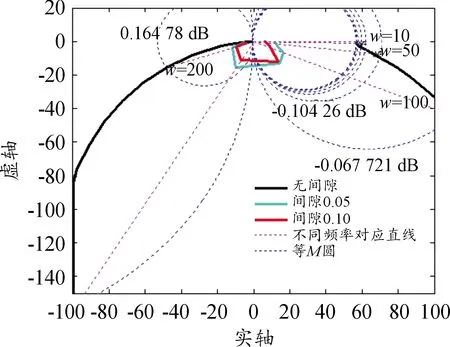
圖9 等M圓與開環幅相曲線

由于系統閉環幅值還需疊加其他部分，通過前文分析，其他部分不受間隙影響，因此，從圖中讀出單位負反饋的閉環幅值的相對變化量與整個系統的閉環幅值的相對變化量是一致的。以w=50 rad/s的頻點為例，如圖10所示，直虛線為系統在w=50 rad/s頻率下對應的直線，虛線圓即為等M圓，等M圓有無數個，每個等M圓對應一個閉環幅值。開環幅相曲線與頻率直線的交點會位于某個等M圓上，從該等M圓可直接讀出系統的閉環幅值。

在w=50 rad/s處，無間隙時，開環幅相曲線與-0.130 dB的等M圓相交，間隙為0.05 mm時，與-0.657 dB的等M圓相交，間隙為0.1 mm時，與-1.155 dB的等M圓相交。在不同間隙下，圖解法與仿真結果比較如表4所示。

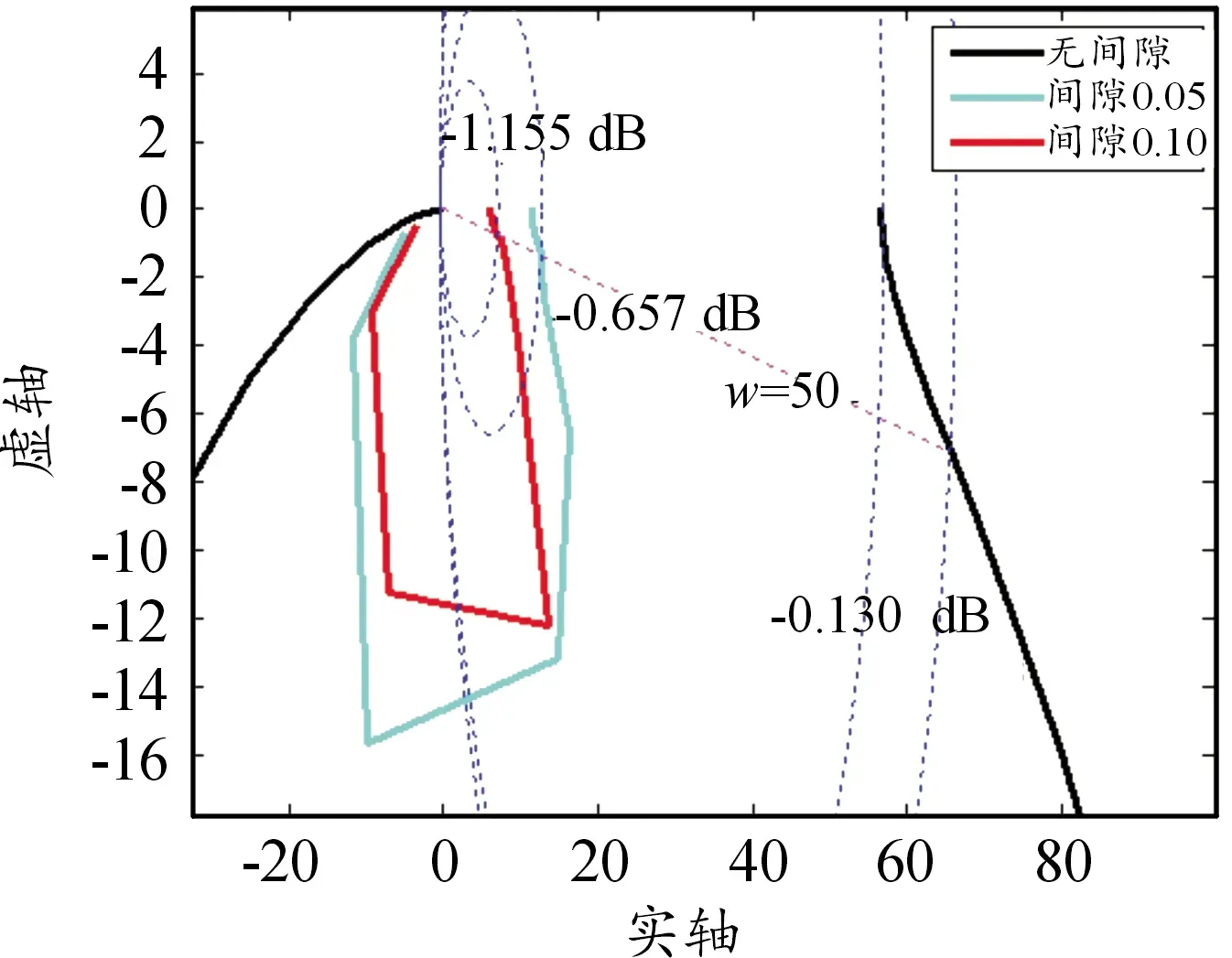
圖10 等M圓與開環幅相曲線相交情況

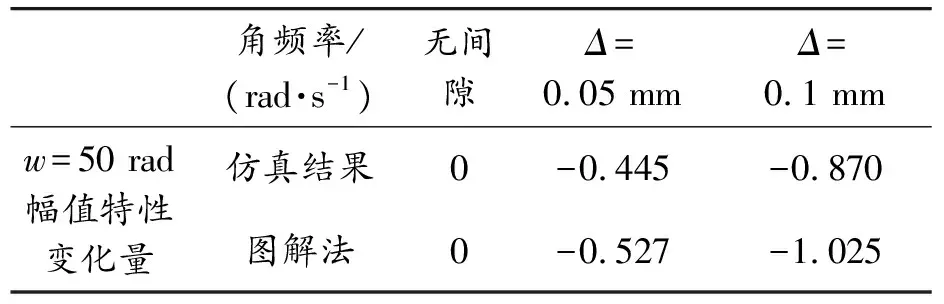
表4 w=50 rad/s幅值相對變化量比較

從表4可以看出，圖解法與仿真結果趨勢一致，具體數值稍有差異。這是由于描述函數是一種近似方法，忽略了高次諧波的影響，在實際系統中，死區環節的輸入并非理想的正弦函數。若只需快速估計出死區非線性對系統影響，圖解法的精度是足夠的。

在等M圓上讀數時有以下特點:

1)N(A)為純比例時，不同間隙，同樣頻率時，系統幅相特性在復平面上都在一條直線上。當該直線穿過較多的圓，即等M圓越密集時，幅值變化較為劇烈，由于等M圓在無窮遠處比較稀疏，在圓心處及靠近0 dB線處比較密集，因此當直線靠近圓心和0 dB線時，幅值變化較大，即開環幅值大時，閉環幅值變化小，開環幅值小時，閉環幅值變化大。

2) 當頻率對應的直線趨近于等M圓的法線時，幅值變化較大。

3) 當頻率對應的直線趨近于等M圓的切線時，幅值變化較小。

上述特點對用等N圓讀取閉環相位時同樣適用。

2.3 系統閉環相位特性

對于單位負反饋系統，通過等N圓可以直接在開環幅相曲線上讀出閉環相位特性。

等N圓也為一簇圓。其方程為

(3)

式中,N=tanφ，φ為閉環頻率特性的相角。

將等N圓疊加到開環幅相曲線上，可以直接讀出閉環相位，如圖11所示。由于頻率對應的直線趨于等N圓的切線方向，因此閉環相位特性變化不大，從圖5和表3的仿真結果也可以印證。

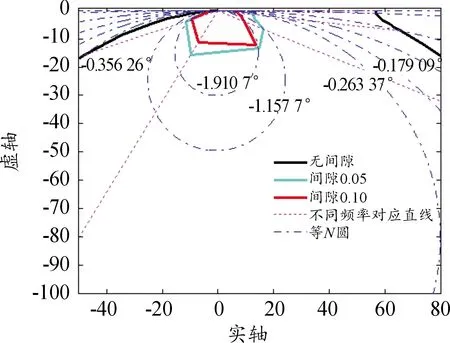
圖11 等N圓與開環幅相曲線

3 閉環內間隙對伺服系統閉環頻率特性的影響

作為圖解法的應用，分析閉環內齒輪傳動間隙對伺服系統閉環頻率特性的影響。圖12為考慮內部間隙的伺服系統模型，化簡為單位負反饋系統，如圖13所示。

取N(A)=1時，得到無間隙時開環幅相特性曲線，同時可得到每個頻率對應的直線，如圖14。與圖7相比，每個頻率的開環幅值均大10倍以上，根據前文總結的圖解法讀圖特點，可知當閉環內間隙變化時，系統閉環頻率特性變化不會很大。用圖12所示模型進行仿真，仿真結果如圖15所示，不同間隙下系統閉環幅值和相位特性基本重合。

圖12 考慮內部間隙的伺服系統模型示意圖

圖13 伺服系統模型等效化簡結果

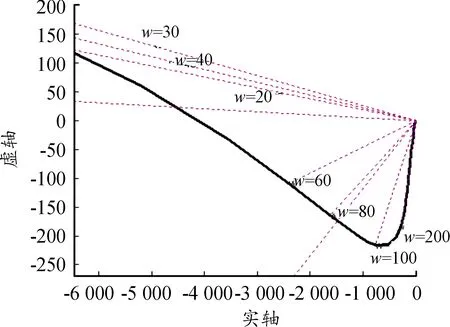
圖14 系統開環幅相曲線

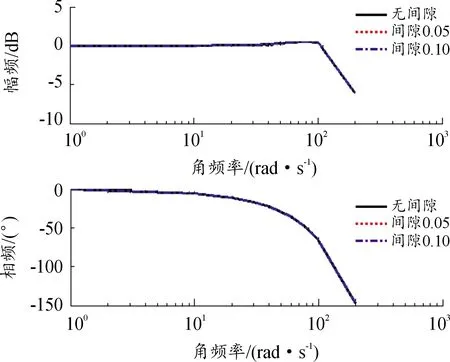
圖15 系統仿真結果曲線

4 試驗驗證

為了驗證仿真及分析結果，進行了電動伺服系統頻率測試試驗。加工尺寸不同的銷軸，使配合間隙分別為0.05、0.1 mm，將伺服機構安裝在負載臺上，試驗結果如圖16所示，其幅值和相位變化趨勢與圖5的仿真結果一致。由于仿真模型中只考慮了負載間隙帶來的死區非線性而未考慮其他非線性環節，因而仿真結果與試驗結果存在一定差異。

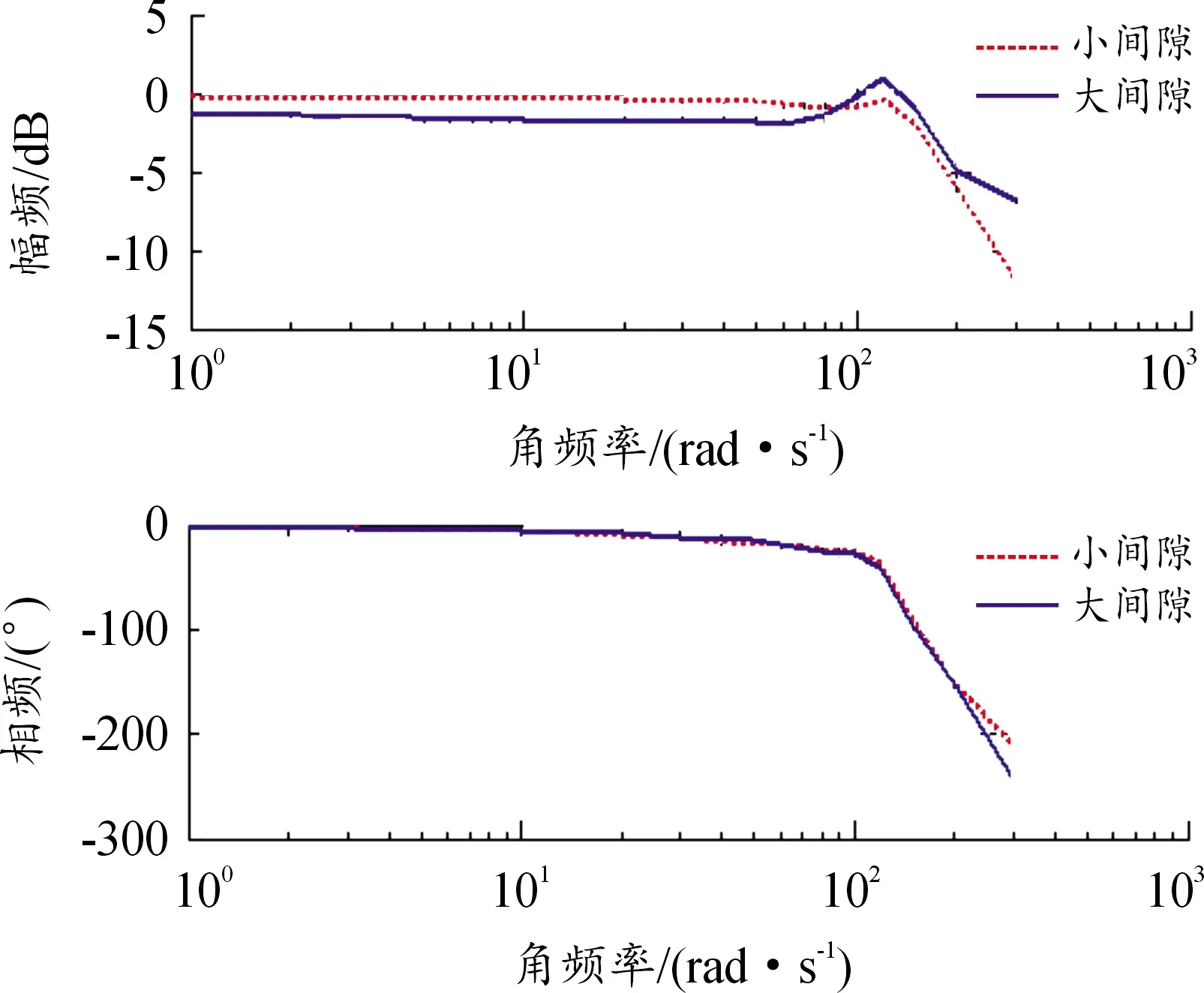
圖16 試驗結果曲線

5 結論

1) 通過等效變換將系統變換為單位負反饋系統，通過等M圓、等N圓及線性部分的開環幅相曲線直觀地觀測到間隙對系統頻率特性的影響。

2) 死區非線性對系統閉環頻率特性的影響取決于不考慮死區環節時的線性部分，將各頻率下幅相特性在復平面上的點與原點連接起來形成一條直線，死區環節的效果是使各頻率對應的點在復平面上沿直線向原點移動。

3) 從圖解法及仿真結果都可得出負載間隙比閉環內的間隙對系統閉環頻率的影響更大。