跨海大橋鋼箱梁內敷電纜夏季極端溫度模擬研究

侯云鴿，章李剛，陳小峰，吳 珂

(1.浙江大學 浙江省海洋巖土工程與材料重點實驗室，浙江 杭州 310058；2.浙江大學 平衡建筑研究中心，浙江 杭州 310007；3.浙江大學 海洋感知技術與裝備教育部工程研究中心，浙江 舟山 316021;4.浙江華云電力工程設計咨詢有限公司，浙江 杭州 310014)

0 引言

利用鋼箱梁內部空間隨橋敷設電纜作為一種新型的跨海輸電形式，因可降低海島地區電力輸送的難度，減少工程建設費用，便于進行搶、檢修工作，應用日益廣泛[1-2]。然而，由于大橋受到太陽的直接照射，夏季箱梁內部溫度極高(可達45 ℃以上)，加之內敷電纜釋放的熱量，使得其內部空氣溫度進一步升高。夏季箱梁內的極端溫度已成為限制電纜載流量提升的關鍵因素。

鋼箱梁內的溫度受外環境溫度、風速以及太陽輻射的共同影響，因而難以預測。針對鋼箱梁的溫度特征，丁幼亮等[3]基于珠江黃埔大橋結構健康監測系統1年的溫度數據，發現扁平鋼箱梁橫截面冬季溫度較低，夏季溫度較高，年溫度變化具有明顯的季節特征。陳一飛等[4]基于北方跨海斜拉橋長期監測系統的數據，發現頂板橫向溫差與頂底板縱向溫差顯著，底板橫向溫差非常小，頂底板溫度橫向分布呈明顯不對稱性，并推算50年重現期下的溫差值。胡堅鋒等[5]通過嘉紹大橋主航道橋典型高溫日鋼箱梁內部溫度測試，發現夏季鋼箱梁結構溫度可達50 ℃以上，大氣溫度、ERS鋼橋面鋪裝各層以及鋼箱梁斷面溫度的相關性較好。孫君等[6]進一步對比了斜拉橋和懸索橋鋼箱梁溫度場的差異。此外，顧穎等[7]采用數值模擬方法對太陽輻射作用下某混凝土箱梁的溫度場進行研究，溫度計算值與實測數據吻合良好。綜上可知，現有研究多是基于短周期內的溫度實測分析，尚缺乏針對鋼箱梁極端溫度特性的研究，而我國規范指出，橋梁的設計使用年限為100～120年[8]，因此研究橋梁全壽命周期內可能出現的溫度極值至關重要。同時，已有研究也并未考慮電纜發熱對箱梁溫度的影響。

采用Fluent、CFX等計算流體動力學軟件對橋隧等的速度場、溫度場進行模擬具有便捷、高效的優點，并可彌補實測數據密度有限、部分物理量測量難度大等不足，其準確性已得到諸多試驗結果的驗證[3, 9-12]。

本研究以舟岱大橋為例，采用計算流體動力學(CFD)模擬技術對鋼箱梁內敷電纜熱環境進行了數值仿真，研究了電纜發熱對鋼箱梁內部溫度場的影響規律，并基于舟山近60年的氣象數據，分析了夏季箱梁內部空氣的極端溫度條件，為確定電纜載流量、保證電纜運行熱安全提供了重要的技術依據。

1 數值仿真模型

1.1 CFD仿真原理

CFD的基本原理是數值求解控制流體流動的微分方程，得出流體流動的流場在連續區域上的離散分布，從而近似模擬流體流動情況。本研究針對鋼箱梁內外氣體的流動特點，基于雷諾平均思想，采用標準k-ε湍流模型進行計算，且流動過程滿足基本的物理規律，即質量、動量、能量守恒定律。模型中所求解的控制方程的通用形式為[13-14]：

(1)

式中，ρ為密度;φ為通用變量，可以代表不同的物理量;t為時間;u為速度;Γ為擴散系數;S是源項。上述微分方程中的4項分別是非穩態項、對流項、擴散項以及源項。

輻射傳熱作為鋼箱梁內外熱量交換的一種重要方式是不可忽略的。本計算采用S2S輻射模型，其公式如下[15]：

Qk=qkAk=(qout,k-qin,k)Ak,

(2)

(3)

式中，Qk為輻射換熱量；qout,k為輻射出去的網格單元k所在表面的熱流密度；qin,k為輻射進來的網格單元k所在表面的熱流密度；Ak為網格單元的面積；εk為網格單元k的表面發射率；σ為Stefan-boltzmann常數；Tk為網格單元k表面的溫度；ρk為反射系數。該模型可計算各個表面之間的輻射換熱，適用于鋼箱梁內敷電纜的仿真研究。

1.2 CFD模型構建

鋼箱梁內熱場分布受外界環境氣流溫度、風速和太陽輻射等因素的共同影響。為全面反映各影響因素的作用，計算域包含了鋼箱梁周邊的外環境區域。鋼箱梁結構分別按照舟岱大橋和嘉紹大橋進行建模，考慮鋼箱梁結構與表面瀝青路面鋪裝。利用六面體網格對整個計算區域進行剖分，如圖1所示，模型總網格數約為426萬。

圖1 全局網格劃分

外部大空間進口設為第1類邊界條件，直接按照氣象資料給定風速和氣溫；外部大空間出口設為第2類邊界條件，即認為物理量的法向梯度為0。開啟太陽輻射模型，以考慮太陽輻射對鋼箱梁內環境溫度的影響。鋼箱梁壁及電纜層設為無滑移、不可穿透壁面邊界條件。在舟岱大橋鋼箱梁模型中考慮布置220 kV，2 500 mm2的電纜，電纜采用三相兩回路，品字形布置，按照實際多層結構進行建模[11]。電纜載流量1 540 A，單根電纜發熱量為47.2 W/m。

1.3 仿真模型校核

將2015年8月3日現場實測環境溫度數據[5]、當地風速數據作為邊界代入嘉紹大橋計算模型，對鋼橋面鋪裝及鋼箱梁斷面溫度進行模擬。由圖2可見，箱梁頂板、底板、橫隔板溫度的模擬結果與現場實測數據均吻合良好。由于17:00大橋采取了人工灑水降溫措施，灑水作業使得路面溫度迅速下降，模擬中無法考慮該過程，因此17:00后模擬得到的瀝青表面溫度相比實測有所偏高。

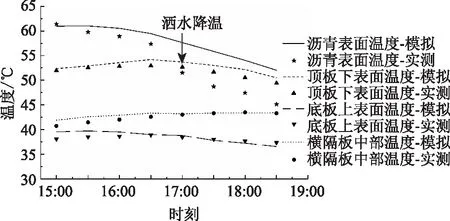
圖2 模擬結果與嘉紹大橋實測結果對比

2 分析與討論

2.1 鋼箱梁內敷電纜熱環境分析

選取主通道工程橋址區極端最高氣溫38.6 ℃作為環境溫度，取最低月平均風速4.0 m/s作為環境風速，并考慮夏至日太陽直射作為夏季典型高溫天氣條件。計算得到無電纜和有電纜敷設時鋼箱梁內部溫度分布，如圖3所示。

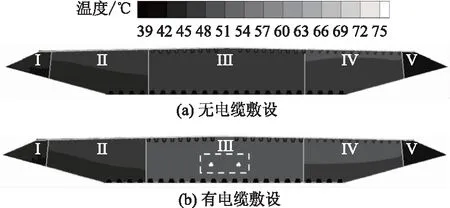
圖3 鋼箱梁內部溫度場

箱梁內部被縱隔板隔成5個腔體，由圖3可以看出，無論是否存在電纜，鋼箱梁內左右兩側腔體均存在較為顯著的溫度梯度，而中間腔體溫度分布較為均勻。左側腔體II相比右側箱體IV溫度稍低，這是由于箱梁外部氣流由左側向右橫掠箱梁，換熱邊界層變厚，換熱系數下降，同時氣流溫度逐步升高，路面對流換熱變差，路面溫度上升，從而使得腔內的溫度上升。

對比敷設電纜前后箱梁內部的溫度分布可以看出，敷設電纜后鋼箱內部平均溫度較無電纜時略大。表1匯總了典型高溫工況鋼箱梁各位置的溫度值。由表1可知，相較于無電纜工況，鋼箱梁內敷設電纜后內部平均溫度升高了2.76 ℃，而鋼箱梁頂板和底板溫度升高相對較少，兩者分別升高0.49 ℃和1.05 ℃。

表1 典型高溫工況鋼箱梁溫度

2.2 鋼箱梁內平均溫度極值重現期

為了進一步分析鋼箱梁內空氣平均溫度可能出現的極值，基于舟山定海58 477國家氣象站1960—2020年的氣象數據(部分年度數據缺失)進行分析。將舟山定海氣象站夏季的逐時氣象參數作為邊界條件代入計算模型，可獲得鋼箱梁內部平均溫度在過去60年中的夏季逐時變化規律，篩選出每一年中鋼箱梁內部平均溫度的小時最高值,如圖4所示。

圖4 鋼箱梁內部平均溫度的年小時最高值

由圖4可知，近60年中鋼箱梁內部空氣溫度的年小時最高值分布在48～57 ℃之間，其中大于52 ℃的有12年，大于55 ℃的有3年。最高溫度出現在1979年，當天晴朗少云，最高氣溫達到40 ℃，同時風速極低，小時平均風速僅為0.5 m/s。

由于氣象要素的出現具有隨機性，在實際應用中常基于統計分析，通過極限氣象要素重現期來描述其出現概率[16-18]。常見的分布函數有：皮爾遜Ⅲ型分布、對數正態分布、耿貝爾分布等[19]，其中皮爾遜Ⅲ分布(以下簡稱P-Ⅲ分布)在分析溫度重現期上的效果要明顯優于對數正態分布、耿貝爾分布[20]。因此，本研究采用P-Ⅲ分布來計算鋼箱梁內平均溫度極值的重現期。

P-Ⅲ分布具有廣泛的概括和模擬能力，其概率密度函數和保證率分布函數分別為：

(4)

(5)

式中,參數x0為隨機變量x所能取的最小值；xp為隨機變量x的p分位數，α為形狀參數；β為尺寸參數；Γ(α)是α的伽馬函數。用矩估計法[21-22]可得3個參數的表達式：

(6)

β=2/σcs,

(7)

(8)

式中,m為數學期望；σ為均方差；Cs為偏態系數；Cv為變差系數，其估計量分別為：

(9)

(10)

(11)

(12)

根據以上公式求得參數及估計量的值見表2。

表2 P-Ⅲ分布參數及估計量值

重現期與鋼箱梁內部平均溫度極值的對應關系如表3、表4所示。

表4 不同鋼箱梁內部平均溫度對應的重現期

結合表3和表4可知，50年一遇和百年一遇的鋼箱梁內部平均溫度極值分別為56.3 ℃和57.2 ℃；而鋼箱梁內部平均溫度達到55 ℃和60 ℃的重現期分別為19.3年和1 129年，可見在鋼箱梁正常服役年限內很難出現60 ℃以上的高溫。

3 結論

(1)利用CFD方法構建了含電纜的鋼箱梁全尺寸熱場數學模型，模型綜合考慮了外界環境溫度、風速和太陽輻射的共同影響，鋼箱梁橫截面的溫度模擬結果與嘉紹大橋的現場實測數據趨勢一致。

(2)鋼箱梁腔體溫度主要受外部氣象條件影響，電纜發熱對鋼箱梁腔體溫度的影響有限，采用雙回路電纜，在1 540 A額定載流量下，鋼箱梁腔體溫升<3 ℃。

(3)基于氣象站的長序列氣象資料可模擬獲取鋼箱梁內部平均溫度的年小時最高值，利用皮爾遜Ⅲ分布可獲得50年一遇和百年一遇的鋼箱梁內部平均溫度極值。