鋼-混凝土混合變截面連續梁橋鋼箱梁段合理長度研究

陳康明，楊洋，吳慶雄, 3，羅健平

(1. 福州大學土木工程學院，福建 福州 350108； 2. 工程結構福建省高校重點實驗室，福建 福州 350108；3. 福建省土木工程多災害防治重點實驗室，福建 福州 350108)

0 引言

鋼-混凝土混合梁橋將橋梁主跨跨中的部分混凝土梁段替換成鋼梁，混凝土梁段與鋼梁在連接部位通過特殊構造形成整體，共同構成橋梁主跨. 鋼-混凝土混合梁的發展始于斜拉橋，在連續梁橋中的應用僅有十幾年. 同預應力混凝土梁橋相比，鋼-混凝土混合梁橋可有效減小主梁的截面尺寸，減輕橋梁自重，提高橋梁跨越能力，同鋼結構梁橋相比，可減少用鋼量，增加結構剛度，提高全橋穩定性，降低工程造價[1-2]. 因此，鋼-混凝土混合梁橋具有較好的應用前景.

目前國內外學者對鋼-混凝土混合梁的研究主要集中于鋼混結合段的受力性能、傳力機理與改進方法等[3-8]. 對于鋼箱梁段合理長度方面的研究相對較少，主要包括：盧桂臣等[9]對鋼箱梁長度比例做了優化研究，確定了舟山桃夭門大橋結合段的合理位置. 張鵬等[10]通過研究結合段不同位置對實橋受力性能、施工難度和工程造價等的影響，確定了結合段的合理位置. 丁威等[11]以一座鋼-混凝土混合連續箱梁橋為背景，討論了鋼箱長度變化時恒、活載作用下結構的力學特征，得到了鋼箱長度與主梁反彎點的位置關系. 蘇慶田等[12]認為邊跨長度和中跨組合梁長度相互影響，并以橋梁結構在運營過程中邊支點不出現負反力作為限制條件，推導了最小邊中跨比和中跨組合梁長度占比之間的關系. 鄧力文[13]以某斜拉橋為研究背景，探討了鋼箱梁段長度比例對主梁受力性能的影響，驗證了結合段位置選取的合理性. 林濤[14]以主跨鋼箱梁長度為變化參數，探討其對恒活載比例分配和主梁恒活載受力特性的影響規律，在綜合考慮結構受力和經濟性基礎上得出了鋼箱梁長度最合理取值. 張少勇等[15]以相同長度的鋼箱梁段自重約為等效混凝土梁自重的30%為原則，比選了甌越大橋中跨的鋼梁段合理長度. 曾明根等[16]以泉州灣跨海大橋為背景，探討了鋼梁長度對混合梁剛構橋受力性能的影響，建議鋼箱梁長度比例取0.4～0.5. 劉曉鳴等[17]對一座混合梁鋼混結合段的具體位置提出了3種方案，綜合考慮了結合段位置處的內力及轉體過程中墩頂處的不平衡彎矩，確定了鋼混結合段位置的合理位置. 黃國紅等[18]基于中墩截面彎矩等效和邊支座支反力控制原則，推導了三跨混合連續梁橋中跨鋼梁長度占比的合理取值范圍.

綜上所述，現有研究主要是針對某一鋼-混凝土混合梁橋，采用有限元方法分析鋼箱梁段長度變化時恒、活載作用下主梁受力性能的變化而確定合理的鋼箱梁長度，因此，其相關研究結果常常不具有共通性，并且在橋梁初步設計階段采用有限元方法顯得較為繁瑣，通過公式進行合理鋼箱梁段長度擬定將更為方便快捷. 現有少量通過理論推導確定鋼箱梁段長度的研究中，主要以中跨鋼梁為等截面的混合梁剛構橋為對象，但變截面鋼梁的力學性能更符合混合梁剛構橋的受力需求.

鑒于鋼箱梁長度是鋼混混合梁的關鍵設計參數，其影響著鋼混混合梁的整體受力性能，合理鋼箱梁長度的確定是鋼混混凝土橋梁往大跨度方向發展時結構受力與經濟性能平衡的難點之一，本研究擬通過建立改進三彎矩法，提出基于改進三彎矩方程的變截面連續梁內力簡化計算方法，并以結構受力和經濟性作為平衡點，得出恒載作用下不同跨徑鋼-混凝土混合連續梁橋最合理的鋼箱梁長度比例，可為鋼-混凝土混合梁設計與應用提供借鑒和參考.

1 基于改進三彎矩方程的變截面連續梁彎矩簡化計算方法

1.1 改進三彎矩方程

三彎矩方程可簡便地用于預估連續梁內力，在結構力學中有著廣泛的應用. 三彎矩方程最早由法國的Clapeyon和Berto于1884年提出，但該方程僅適用于支座等高、跨徑相等并且承受均布荷載的連續梁的內力計算[19]. 后來，德國的Schaffler等將方程組推廣到適用于支座不等高的情況，法國的Blaise進一步將方程推廣到跨徑不等并且荷載任意分布的情況[20]. 三彎矩方程的基本假設為： 材料為彈性體，變形較小，不考慮剪切與軸向變形的影響，支座無沉降，且連續梁支座兩側截面的轉角相等. 三彎矩方程的表達式為：

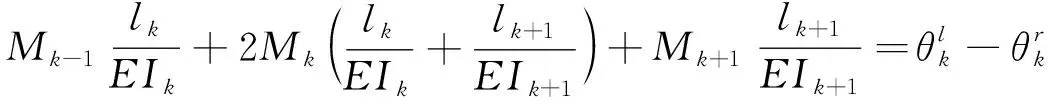
(1)

既有三彎矩方程的一般表達式可適用于不同跨內主梁截面不同，但同一跨內主梁截面必須相同的情況，因此，既有三彎矩方程無法用于常見的變截面連續梁橋的內力計算. 為此，本節基于現有的三彎矩方程一般表達式，推導適用于三跨變截面連續梁的改進三彎矩方程.

已知三彎矩方程本質是根據支座兩邊相對轉角為零的平衡關系建立的一個平衡方程. 對于三跨變截面梁，根據變截面類型分為Ⅰ型、Ⅱ型和Ⅲ型, 如圖1所示，分別代表左邊跨、右邊跨和主跨. 設面內抗彎慣性矩I(t)=I0×f(t)，可以得到不同類型的f(t)表達式：

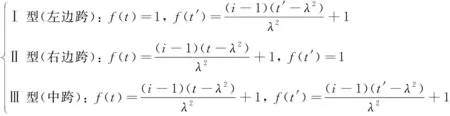
(2)

式中:λ為變截面懸臂長度;i=Imax/Imin，Imax為截面最大慣性矩;Imin為截面最小慣性矩.

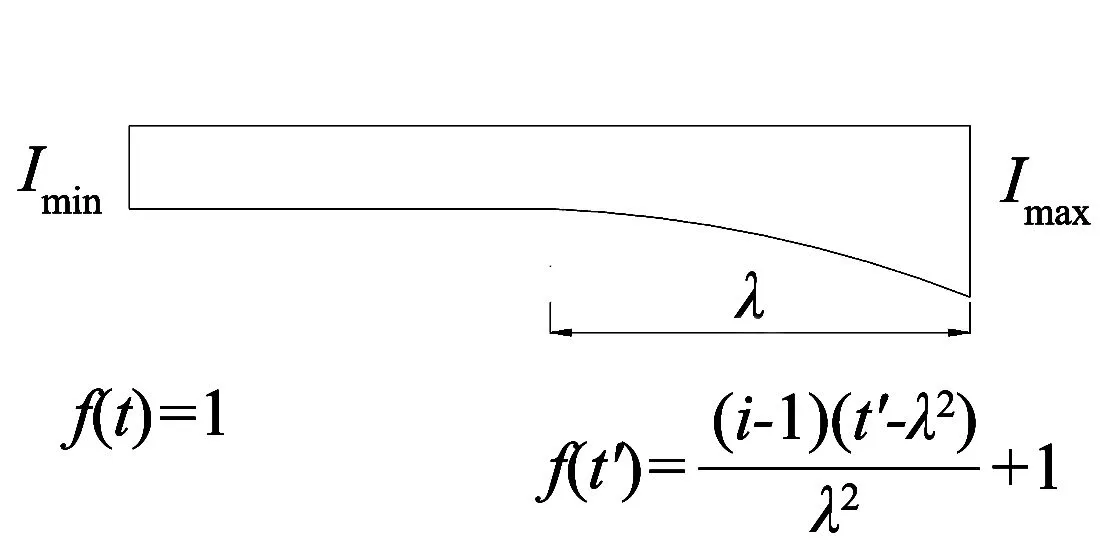
(a) Ⅰ型

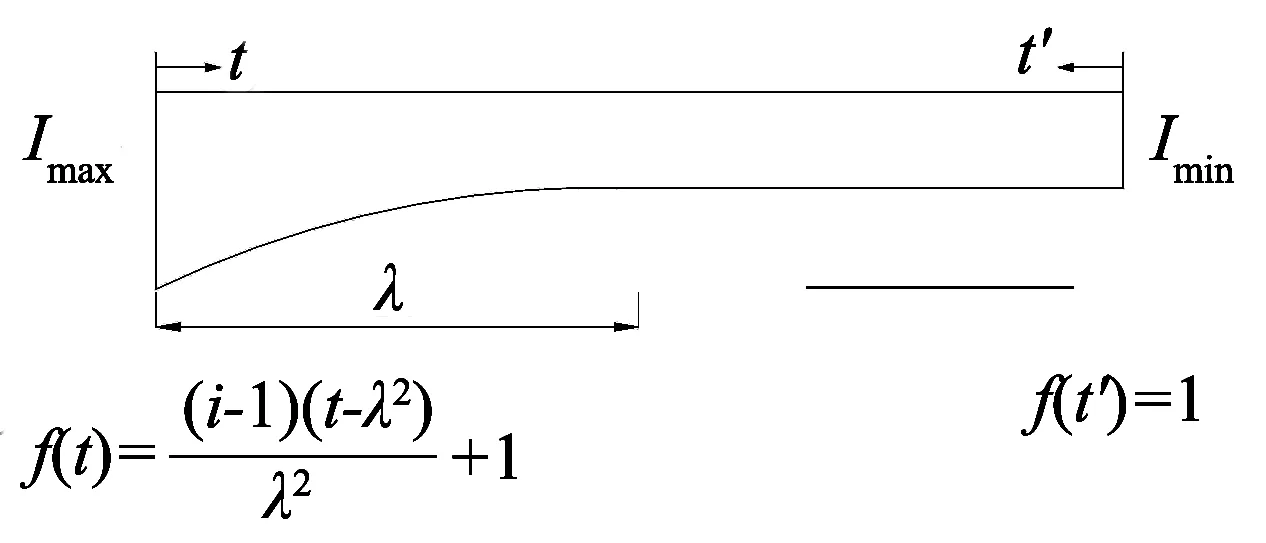
(b) Ⅱ型

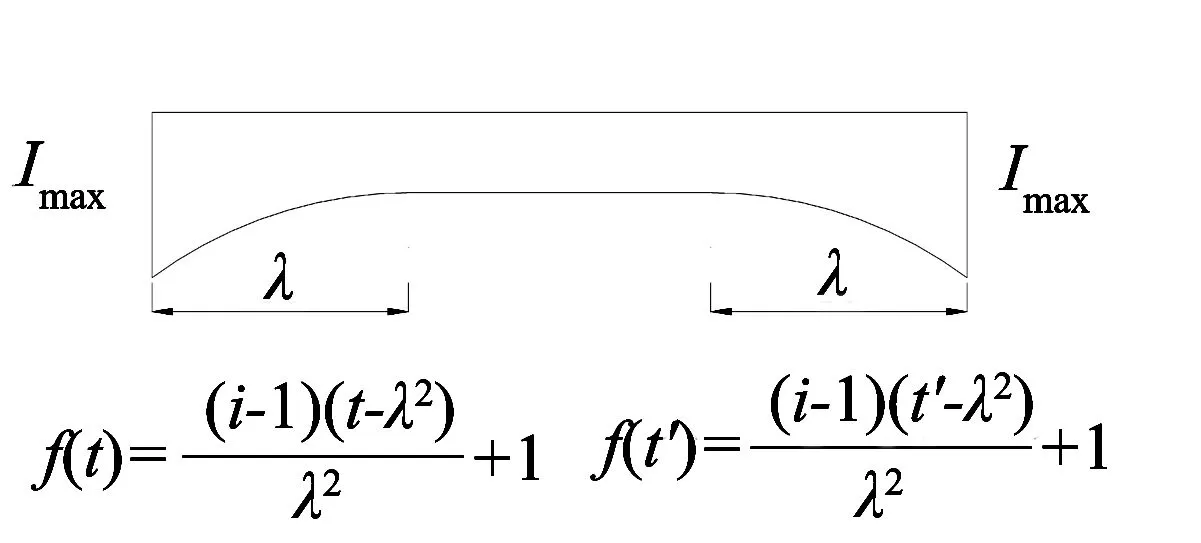
(c) Ⅲ型

由結構力學可以得到簡支梁支點截面A、B的轉角計算式為：

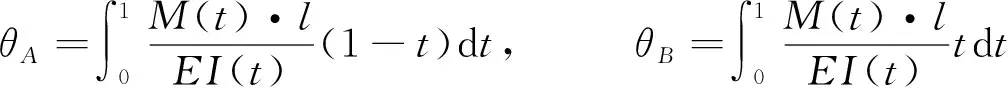
(3)

將變截面梁慣性矩方程式(2)代入下面的支座位置轉角計算公式，可以得到變截面梁在外荷載作用下支座處產生的轉角，從而得到改進三彎矩方程的表達式：

(4)

由于考慮了單跨內變截面梁抗彎慣性矩不同的影響，使得改進三彎矩方程適用于單跨內截面不同、不同跨內截面不同的變截面連續梁彎矩簡化計算.

1.2 基于改進三彎矩方程的變截面連續梁彎矩簡化計算方法

將如圖2所示的三跨變截面連續梁橋看成三個單跨有支點彎矩的簡支梁，根據三彎矩方程每相鄰兩跨可列出一個三彎矩方程，故三跨連續梁可以列出兩個三彎矩方程并聯立求解，見下式：

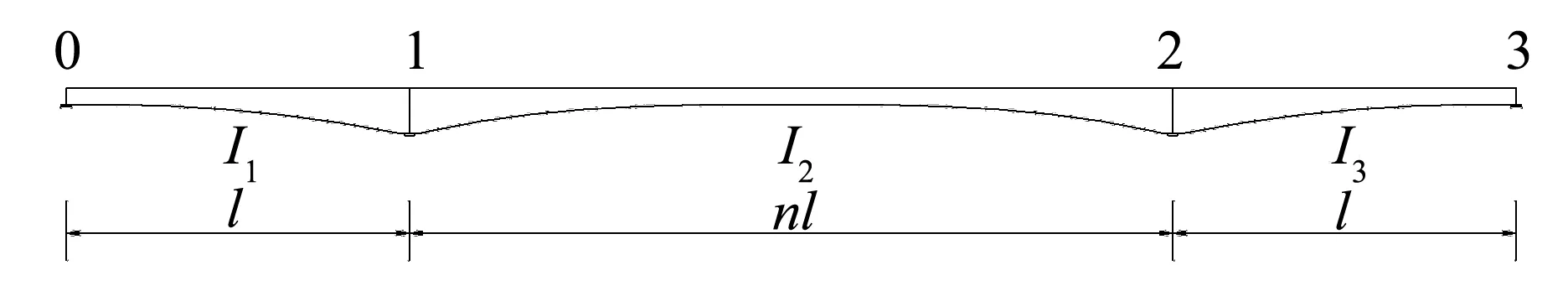
圖2 三跨變截面連續梁橋Fig.2 Three-span variable cross-section continuous beam bridge

式中:l為邊跨跨徑;nl為主跨跨徑;I1、I2和I3為左邊跨、主跨和右邊跨截面抗彎慣性矩.

根據連續梁結構特性和結構左右對稱，可以得到：

M1=M3=0，M1=M2

(6)

將式(6)代入式(5)，整理后可以得到支點彎矩計算公式：

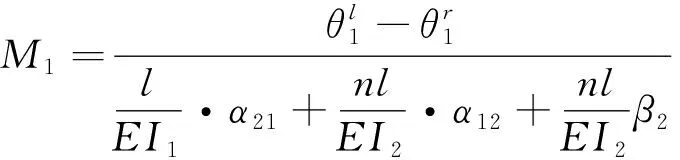
(7)

式(7)中各系數計算如下式所示.

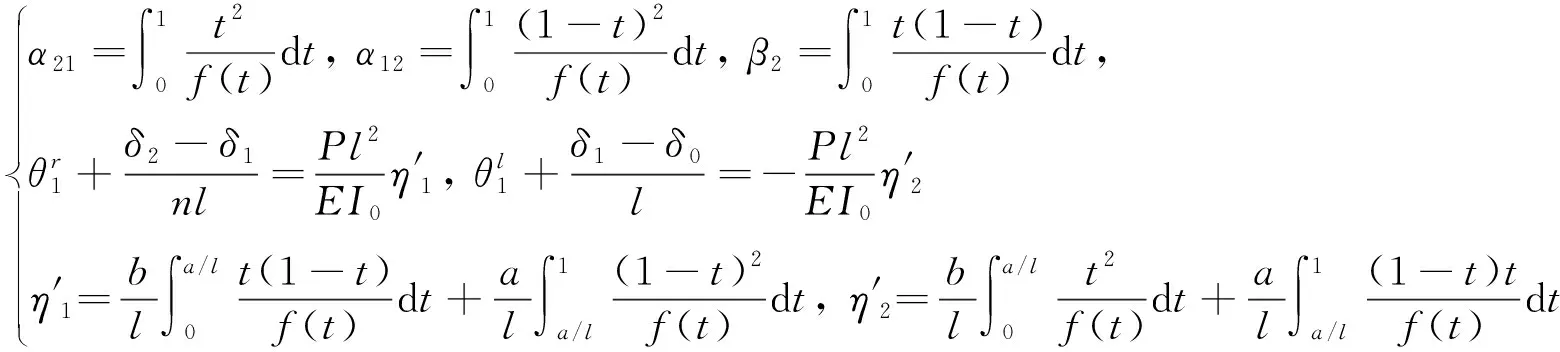
(8)

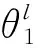
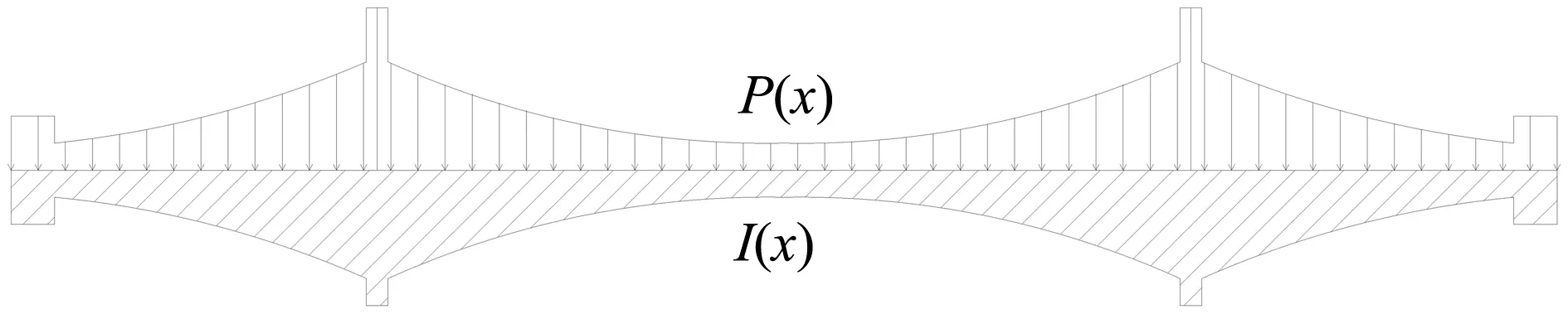
圖3 恒載作用和變截面梁抗彎慣性矩示意Fig.3 Dead load and moment of inertia of section

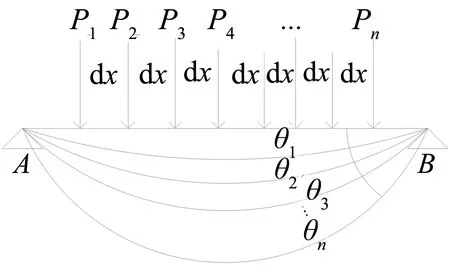
圖4 恒載作用下支點轉角疊加Fig.4 Superposition of rotation angles under dead load

1.3 精度分析

以一座三跨混凝土變截面連續梁橋和一座三跨鋼-混凝土變截面混合連續梁橋為對象，分別采用本研究提出的內力簡化計算方法和桿系有限元方法計算主梁墩頂彎矩和主跨跨中彎矩，通過與有限元計算結果進行的對比分析，驗證基于改進三彎矩方程的變截面連續梁彎矩簡化計算方法的精度.

混凝土變截面連續梁橋的橋跨布置為(65+110+65)m，采用單箱單室截面，跨中梁高2.8 m，支點梁高6.6 m，梁高采用二次拋物線規律變化，梁寬6.5 m，左右懸臂長各2.75 m. 箱梁跨中頂板厚30 cm，腹板厚60 cm，中支點根部底板厚150 cm，跨中底板厚30 cm. 主梁采用C50混凝土.

鋼-混凝土混合變截面連續梁橋的橋跨布置為(67.5+150+67.5)m，其中主跨跨中60 m梁段為鋼箱梁，其余梁段為混凝土梁. 混凝土梁采用單箱單室截面，鋼箱梁采用單箱雙室截面，跨中梁高3.3 m，支點梁高8.8 m，梁高采用二次拋物線規律變化，梁寬7.8 m，左右懸臂長各3.3 m. 箱梁跨中頂板厚28 cm，腹板厚度從根部71 cm變化至跨中48 cm，中支點根部底板厚100 cm，跨中底板厚30 cm. 混凝土主梁采用C50混凝土，鋼主梁采用Q345鋼材.

將跨徑、主梁截面尺寸以及材料等相關信息輸入自編的基于改進三彎矩方程的變截面連續梁內力簡化計算程序，得到的彎矩示于圖5. 同時，采用MIDAS/Civil軟件建立混凝土變截面連續梁橋和鋼-混凝土混合連續梁橋的有限元模型，求得的有限元計算結果也示于圖5.

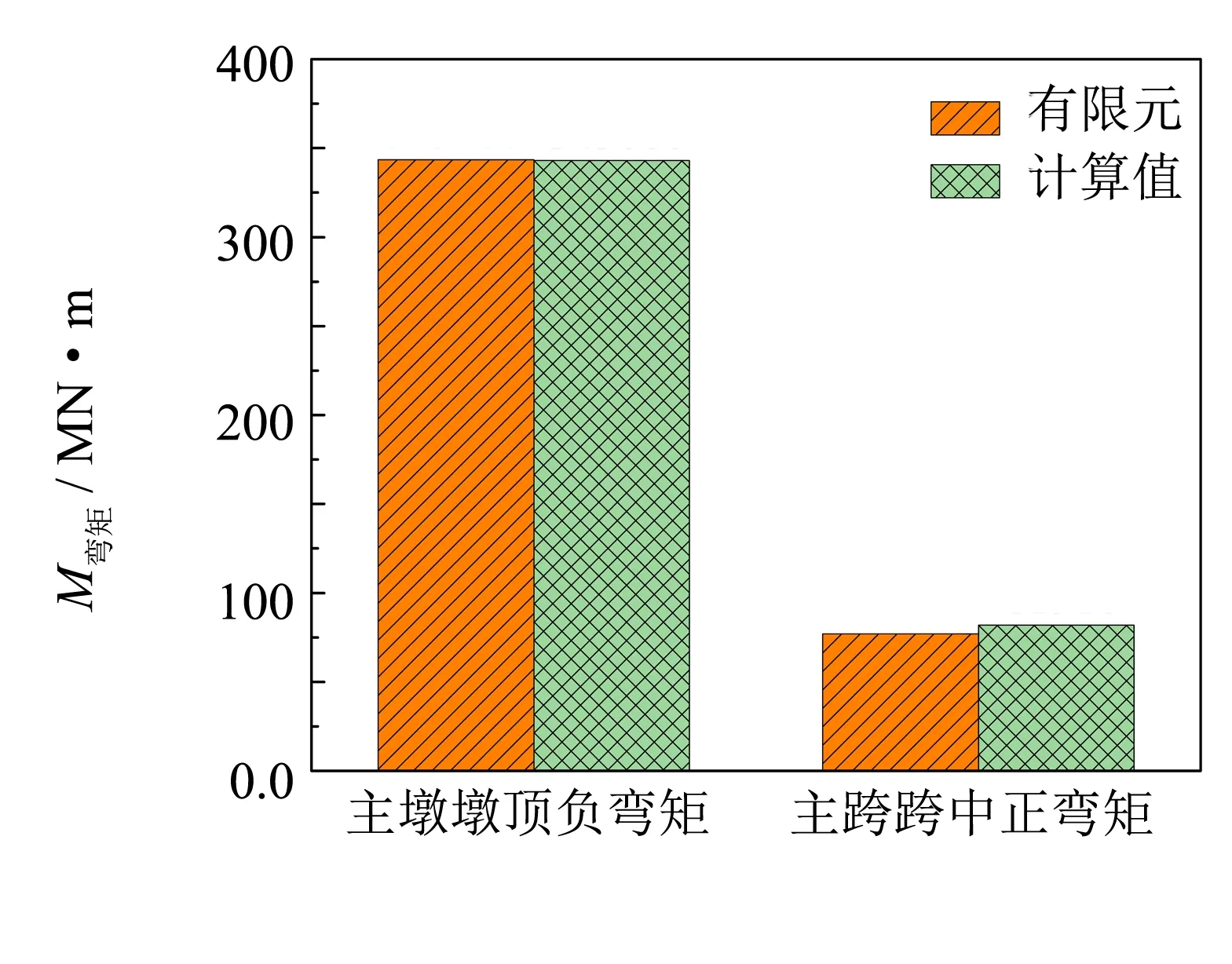
(a) 三跨變截面混凝土連續梁橋

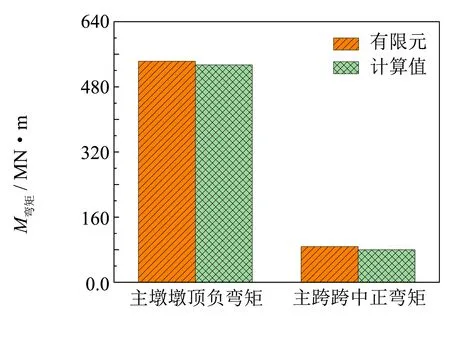
(b) 三跨變截面鋼-混凝土混合連續梁橋

從圖5可知，提出的簡化計算方法的計算結果與有限元計算結果吻合較好，計算精度在90%以上，因此，采用本研究提出的改進三彎矩方程可以便捷且準確地計算恒載作用下三跨變截面混凝土連續梁橋和三跨變截面鋼-混凝土混合連續梁橋的彎矩.

2 鋼-混凝土混合連續梁橋鋼箱梁段合理長度分析

2.1 三跨鋼-混凝土混合變截面連續梁橋標準結構的構建

為使混合連續梁橋鋼箱梁段合理長度分析結果更具代表性，共收集41座國內已建和在建鋼-混凝土混合連續梁橋相關資料[21]，將主跨跨徑分為125 m≤Lm<175 m，175 m≤Lm<225 m，225 m≤Lm<275 m，275 m≤Lm<325 m四個范圍，通過統計分析得到四個范圍內鋼-混凝土混合連續梁的主要構造參數，構建了150、200、250、300 m四個不同主跨跨徑的三跨鋼-混凝土混合變截面連續梁橋標準結構.

以主跨150 m的鋼-混凝土混合變截面連續梁橋標準結構為例，其邊中跨比為0.45，鋼箱梁段長度比例為0.40，跨中高跨比為1/45.6，墩頂高跨比為1/17.1，主梁梁高按二次拋物線變化. 混凝土主梁采用C55混凝土，截面形式為單箱單室直腹板截面，箱梁梁高從8.8 m變化至3.3 m； 頂板寬14.4 m，箱梁寬7.8 m； 頂板厚28 cm，翼緣厚度取50 cm，變厚度底板厚從根部100 cm變化至跨中30 cm，腹板厚度從根部71 cm變化至跨中48 cm(考慮到梗腋對結構受力影響較小，為簡化計算，不設置梗腋). 鋼箱梁主梁采用Q345鋼，截面形式為單箱雙室直腹板截面，交界處梁高根據整體梁高變化取4.192 m，加勁肋統一采用扁肋形式，厚度為20 mm，其余板厚為40 mm. 總體布置與標準斷面見圖6.

(a) 總體布置圖(單位：m)

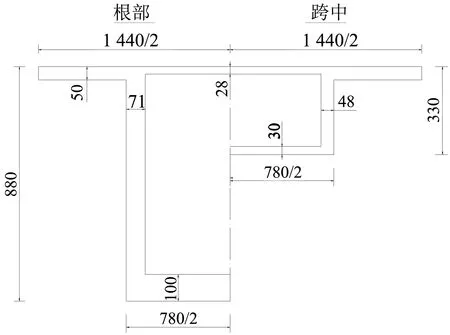
(b) 混凝土主梁橫截面(單位：cm)

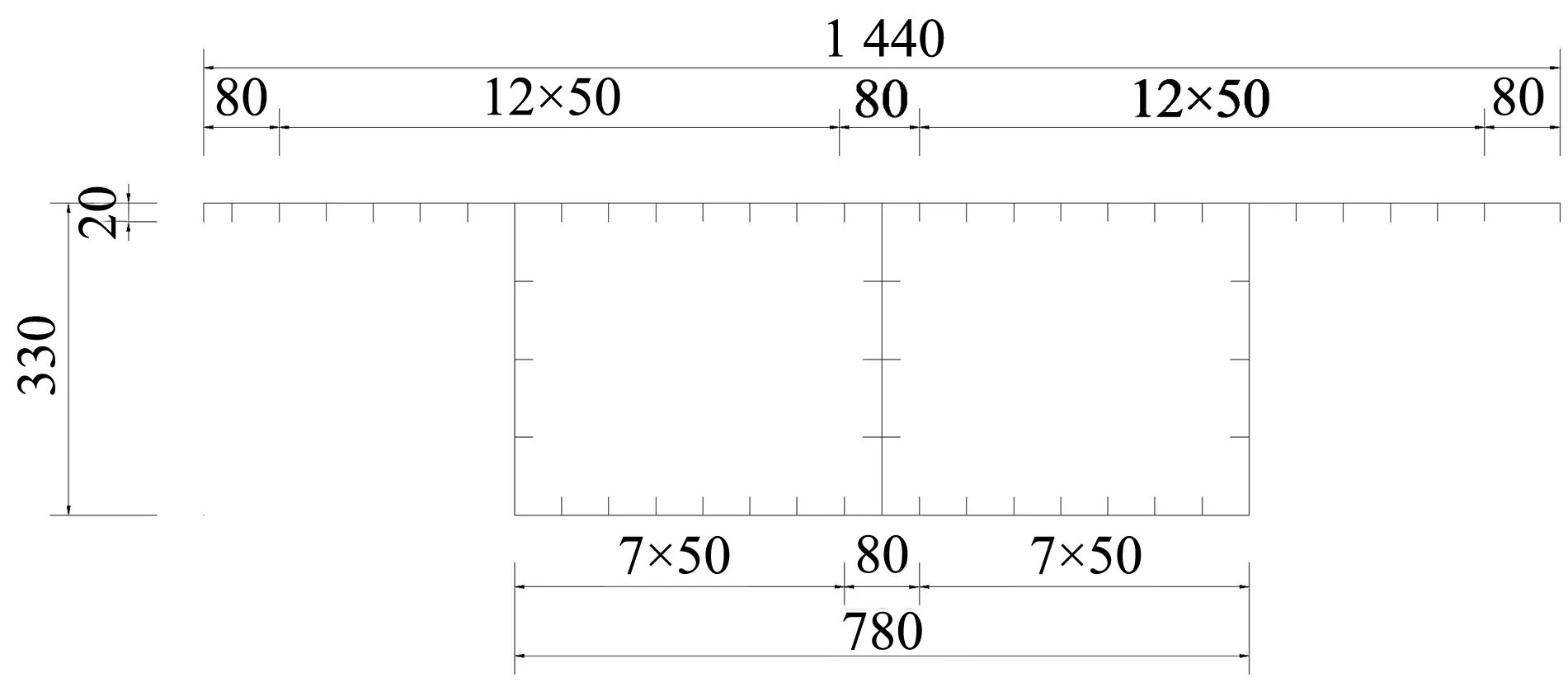
(c) 鋼箱梁橫截面(單位：cm)

2.2 鋼箱梁段合理長度分析

采用構建的主跨跨徑150、200、250和300 m的三跨鋼-混凝土混合變截面連續梁橋標準結構，通過改變鋼箱梁段長度與主跨跨徑的比例，變化范圍為0.2～0.5，采用改進三彎矩方程求得恒載作用下不同跨徑鋼-混凝土混合連續梁橋的主梁墩頂最大負彎矩和主跨跨中最大正彎矩，示于圖7.

從圖7可以看出，隨著鋼箱梁段長度比例的逐漸增大，鋼-混凝土混合梁主墩墩頂負彎矩和主跨跨中正彎矩均逐漸減小，且主跨跨徑150、200、250和300 m的鋼-混凝土混合梁在鋼箱梁長度比例分別為0.35、0.40、0.40和0.45時，主跨跨中正彎矩減小趨勢變緩. 鑒于同跨徑的鋼-混凝土混合連續梁橋的造價隨鋼箱梁段長度的增加而增加[10, 14, 21]，因此，從結構受力與橋梁造價上綜合考慮，主跨跨徑150、200、250和300 m的鋼-混凝土混合變截面連續梁橋鋼箱梁段合理長度與主跨跨徑的比例可取為0.35、0.40、0.40和0.45.

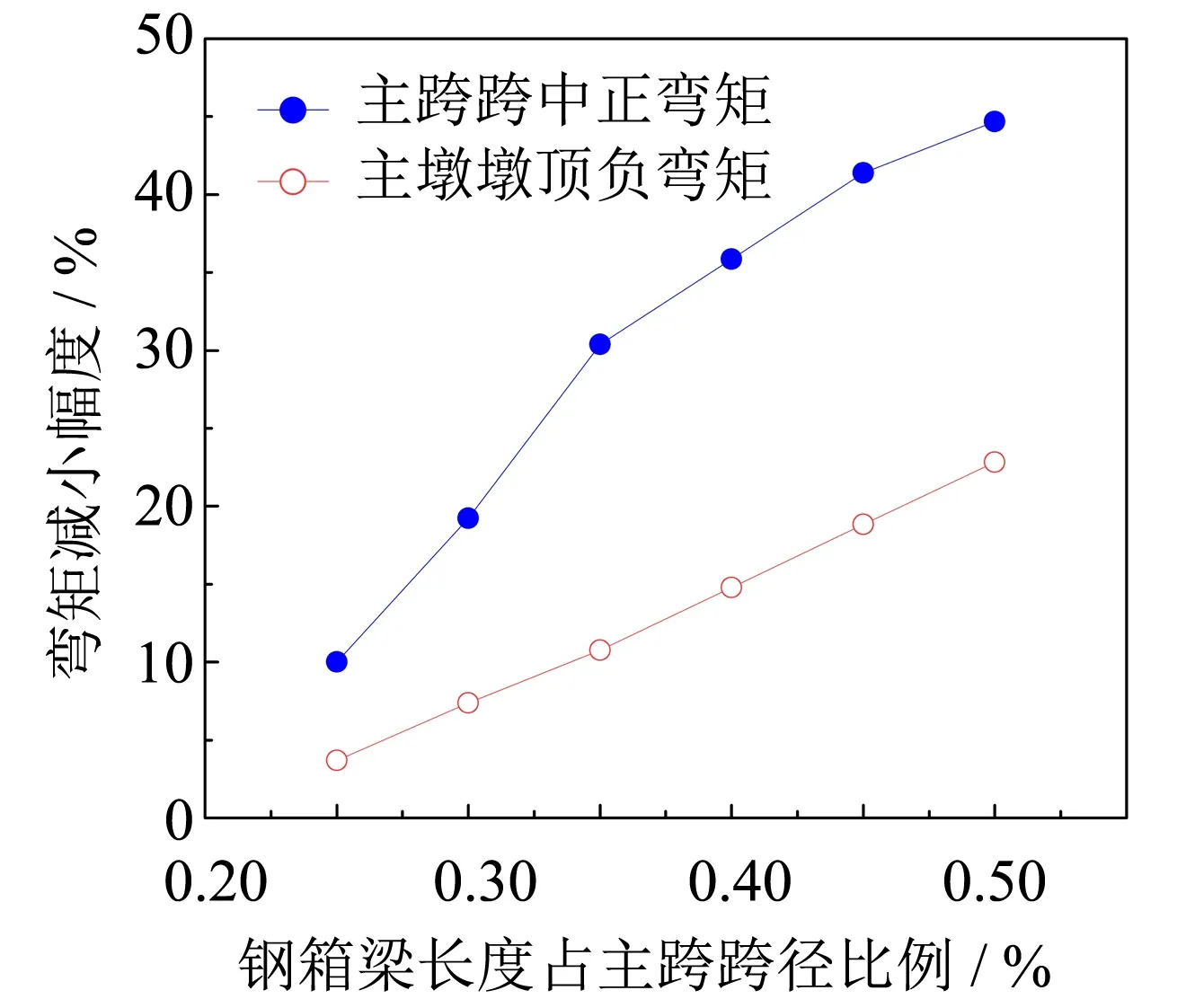
(a) 主跨跨徑150 m

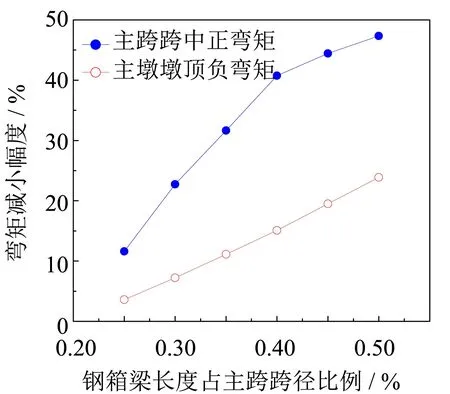
(b) 主跨跨徑200 m

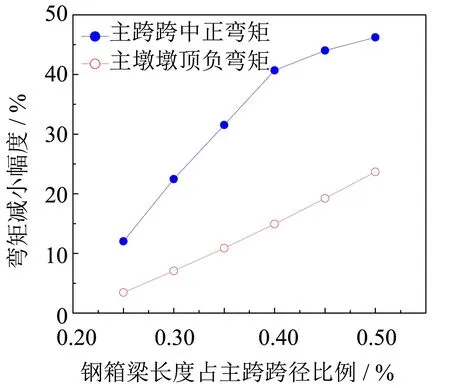
(c) 主跨跨徑250 m

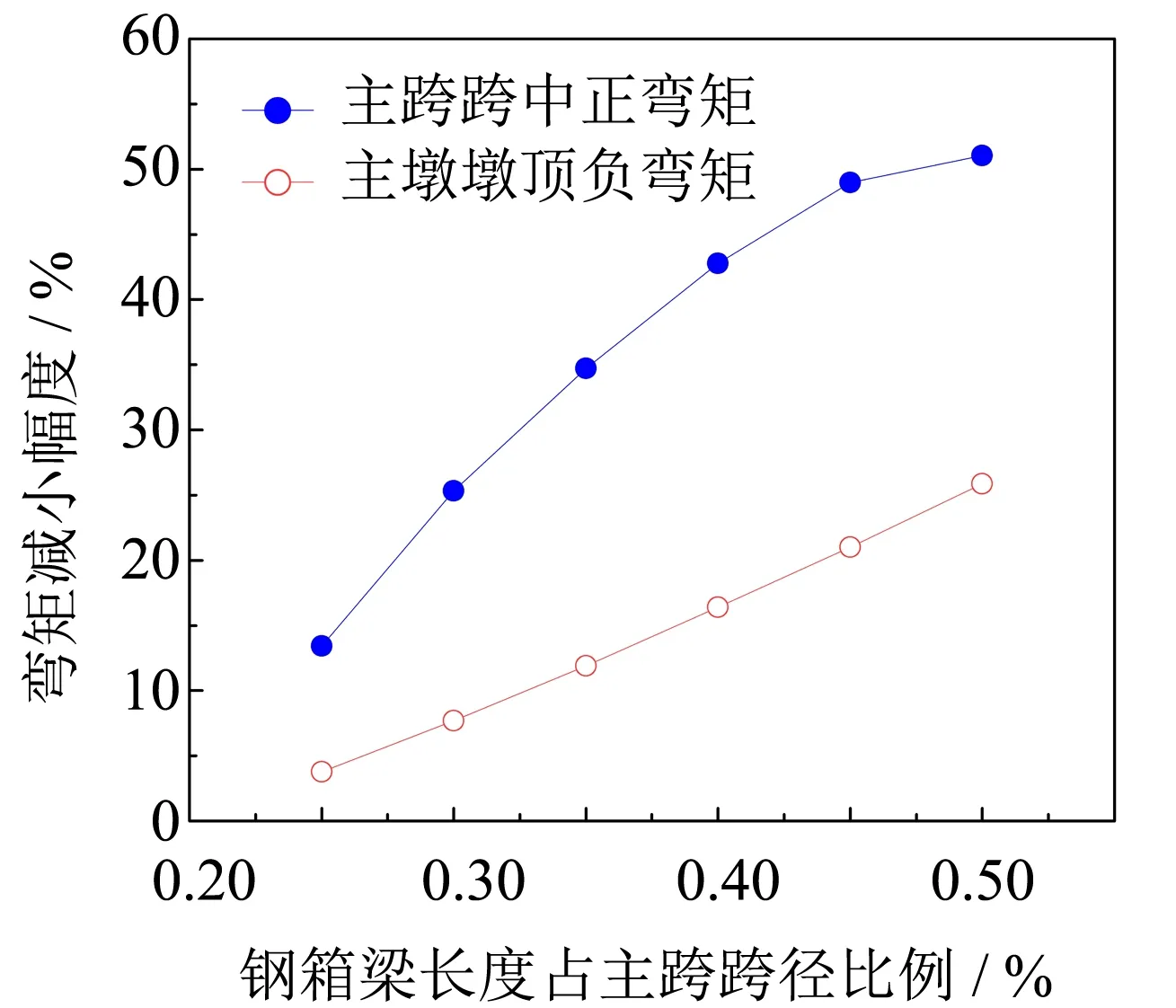
(d) 主跨跨徑300 m

將主跨跨徑Lm=150、200、250和300 m的鋼-混凝土混合變截面連續梁橋合理鋼箱梁段長度比例繪于圖8，通過擬合得到鋼-混凝土混合變截面連續梁橋鋼箱梁段合理長度Lm, s的預估公式：

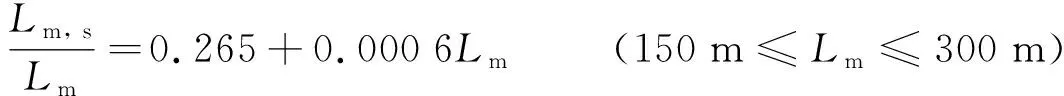
(9)

預估公式(9)的合理性分析如圖9所示，圖9中散點是以已建和在建鋼-混凝土混合連續梁鋼箱梁長度比例為縱坐標，以采用預估公式(9)求得的計算結果為橫坐標，線條代表不同的計算精度. 從圖9可以看出： 預估公式(9)的計算結果與實橋使用的鋼箱梁段長度之間的差在12.5%以內，具有良好的合理性.

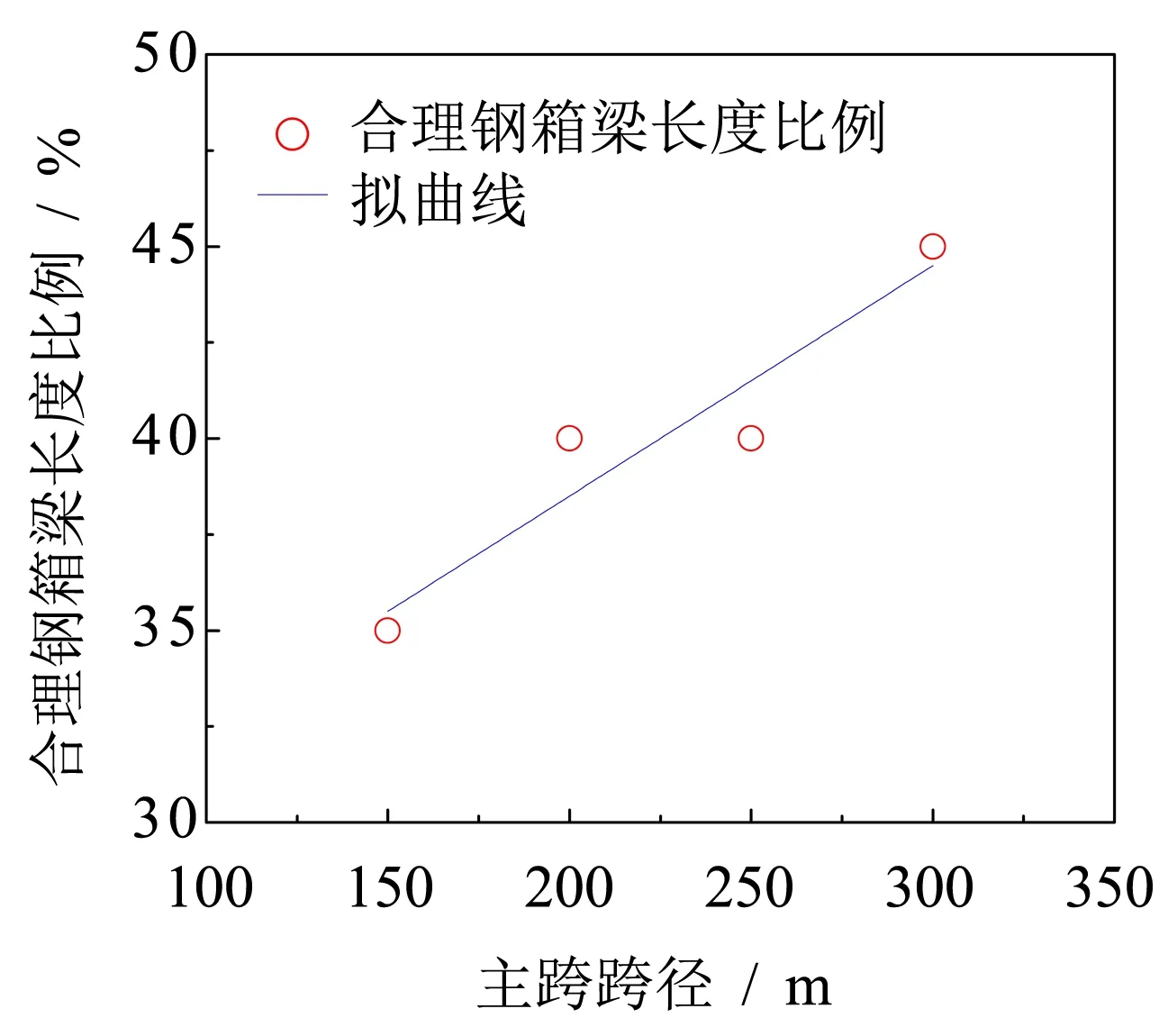
圖8 鋼箱梁段合理長度 Fig.8 Reasonable length of steel box girder

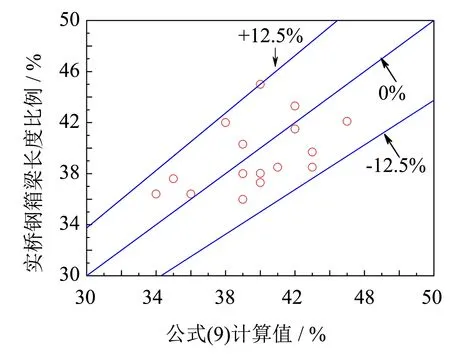
圖9 公式(9)合理性分析Fig.9 Rationality of formula (9)

3 結論

1) 在現有轉角平衡三彎矩方程的基礎上，推導了改進三彎矩方程，建立了基于改進三彎矩方程的變截面連續梁彎矩簡化計算方法. 與混凝土變截面連續梁橋和鋼-混凝土混合連續梁橋有限元計算結果相比，基于改進三彎矩方程的變截面連續梁簡化計算方法的精度在90%以上，可便捷且準確地計算變截面連續梁彎矩.

2) 構建了不同跨徑的鋼-混凝土混合變截面連續梁橋標準結構，混合梁墩頂負彎矩和主跨跨中正彎矩均隨鋼箱梁段長度的增大而減小，主跨跨徑150、200、250和300 m的鋼-混凝土混合梁鋼箱梁段長度與主跨跨徑的比例分別為0.35、0.40、0.40和0.45時，主跨跨中正彎矩減小趨勢變緩.

3) 建立了主跨跨徑在150～300 m間鋼-混凝土混合連續梁橋鋼箱梁段合理長度預估公式，與實橋使用的鋼箱梁段長度之間的差在12.5%以內.