借助GeoGebra軟件分析疑難物理問題
吳彬彬

在初中物理教學中,探究平面鏡成像特點是要求學生操作的實驗項目。實驗中,學生用茶色玻璃板代替平面鏡探究像距和物距的關系,得到像距略大于物距的結果。究其原因在于,教師往往將問題歸結于玻璃板厚度,認為玻璃板厚度與像距物距之差在數值上大致相等,而選用薄玻璃板供學生做實驗。其實,像距和物距的差值比玻璃板厚度要小很多。在玻璃板很薄的情況下,差值可以忽略不計,師生可以得出平面鏡成像實驗中像距與物距相等的結論[1]。為什么在實驗中像距和物距不等?像距和物距的差值到底和玻璃板的厚度有什么關系?筆者將運用GeoGebra軟件分析原因,并動態改變玻璃板厚度引導學生觀察像距和物距的差值變化情況。
一、利用光路圖分析人眼“透玻觀物”的情況
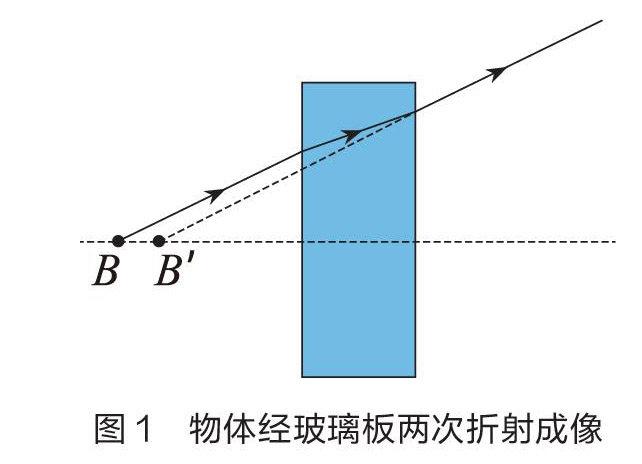
實驗中,學生將蠟燭B放在蠟燭A的像的位置,需要透過玻璃板觀察玻璃板后面蠟燭B的情況。當蠟燭B與蠟燭A的像重合時,蠟燭B的位置就是蠟燭A像的位置。實際上,當實驗者透過玻璃板觀察后面的物體時,看到的其實是經過玻璃板兩個表面折射后形成的虛像,此虛像的位置與物體的位置并不重合(如圖1)。
二、應用GeoGebra軟件動態分析像距和物距的差值
GeoGebra軟件是一款結合幾何、代數與微積分的數學軟件。筆者研究后發現,運用該軟件可分析疑難物理問題,將抽象的問題直觀、動態地呈現在學生面前,以提高實驗或者問題分析的可視化程度[2]。
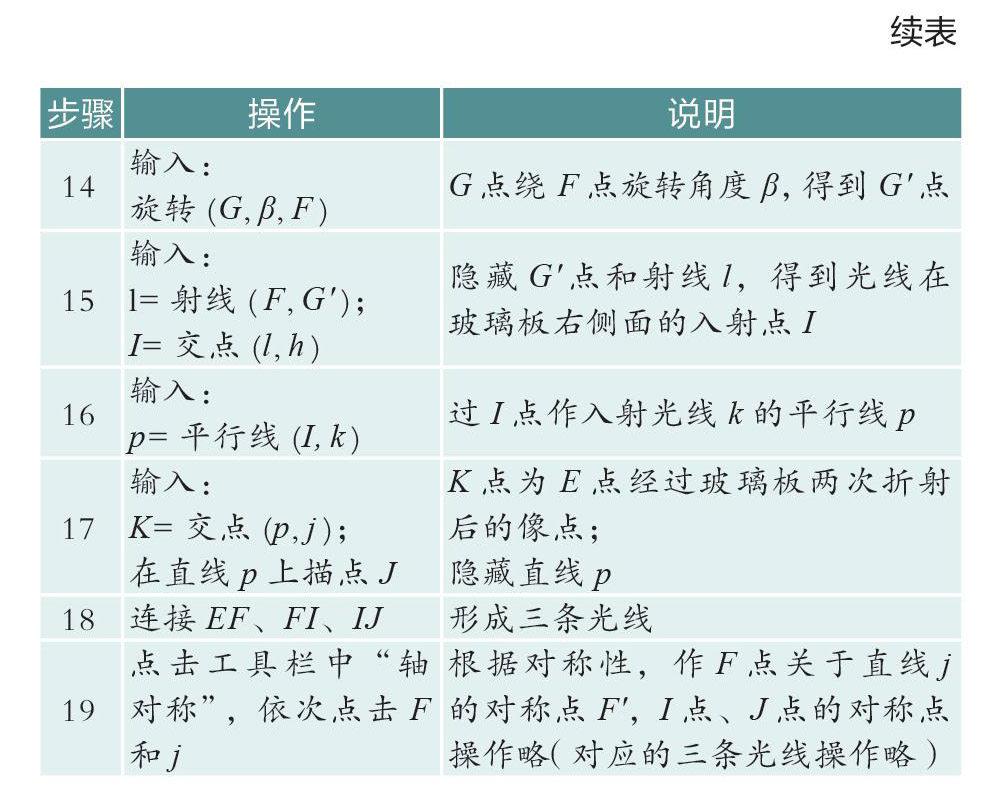
筆者打開GeoGebra軟件,按以下步驟演示和操作(見表1)。
師生通過一系列的操作,得到了成像圖(如圖2),其中K'點為蠟燭A的位置,K點為蠟燭A的像的位置,E點為蠟燭B的位置。實驗者站在玻璃板右側通過玻璃板觀察蠟燭A的像和玻璃板后面蠟燭B,當兩者重合時,可知蠟燭B到玻璃板右側的距離(像距)并不等于蠟燭A到玻璃板右側的距離(物距)。
為方便研究,筆者將所有點和線的標簽隱藏掉,重新命名,并將玻璃板厚度分別調為5、3、1,讓學生觀察對應的像距和物距的差值,分別為1.83、1.1、0.37(如圖3)。學生由此得出三個結論:(1)光的折射導致測得的像距與物距不等,且像距大于物距;(2)像距與物距的差值比玻璃板厚度小,當玻璃板的折射率為1.5時,前者大約是后者的0.37倍;(3)像距與物距的差值隨玻璃板厚度減小而減小。
學生推理得知,當玻璃板很薄時,像距與物距的差值可以忽略,繼而得出像距與物距相等的結論。在平時的實驗中,教師選擇較薄的玻璃板做實驗是有道理的。
為方便作圖,以上模擬中的入射角比較大,這與人眼觀察視角并不相符。筆者將入射角盡量調小,將玻璃板厚度調為1,得到像距和物距的差值為0.33。筆者保持入射角不變,逐漸增大玻璃板厚度,計算像距和物距的差值(見表2)。
根據表2中的數據,學生發現像距和物距的差值約為玻璃板厚度的1/3,兩者之間有明確的關系。
三、幾何證明像距和物距的差值與玻璃板厚度的關系
筆者進行如下設置:設玻璃板的厚度為d,玻璃的折射率為n,蠟燭A與玻璃板右表面的距離為物距u,蠟燭B與玻璃板右表面的距離為像距v,蠟燭B發出的光線經過玻璃板左表面折射的入射角和折射角分別為α和β(如圖4)。
根據幾何關系可得:
utanα-dtanβ= (v-d) tanα。
整理可得: (u-v+d) tanα=dtanβ。
實驗者在AB連線附近觀察時,入射角α比較小,此時滿足tanα≈sinα、tanβ≈sinβ,即 (u-v+d) sinα=dsinβ;將折射定律的關系式n=?????????代入可得v-u=d。
由于玻璃的折射率n一定,所以像距和物距的差值與玻璃板的厚度d成正比。玻璃折射率n取1.5代入時,兩者之間確實是成比例的關系,與之前運用GeoGebra軟件模擬的結果相符。
四、總結
學生探究光的折射問題被安排在平面鏡成像教學之后,在新授課過程中,教師無法給學生解釋其中原因。但是在復習過程中,教師完全可以利用這個“真實驗”中發現的“真問題”帶領學生鞏固相關知識。在初中物理教學過程中有許多抽象而復雜的問題,教師無法用現有的知識或利用現成的實驗器材為學生解答,此時可以借助GeoGebra等教學軟件進行模擬分析,引導學生觀察、探究和思考。教師只有在教學中不斷充實自己知識儲備,提高專業素養,優化教學方法,才能高效教學,科學育人。
注:本文系江蘇省教育科學“十三五”規劃2020年度立項課題“基于TPACK理念的中學物理微課設計策略研究”(課題編號:D/2020/02/151)的研究成果。
參考文獻
[1] 李琴,蔣長春.基于認知結構優化的復習課教學策略[J].中學物理,2021(14):54-56.
[2] 劉健智,程婷.GeoGebra軟件在物理可視化教學中的應用[J].物理教師,2021(6):70-73.
(作者系江蘇省蘇州市相城區春申中學教師)
責任編輯:祝元志

