LINGO軟件在高中數(shù)學建模中的應用研究

張峰，米永強

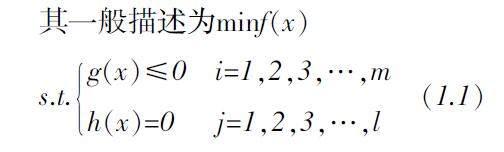
摘? 要：文章在對高中數(shù)學的六大核心素養(yǎng)之一的數(shù)學建模和高中數(shù)學建模中的優(yōu)化問題的研究基礎上，針對高中數(shù)學建模競賽中涉及的線性規(guī)劃問題和0-1規(guī)劃問題，給出了利用LINGO軟件求解農(nóng)場作物種植和大學生選課策略這兩個案例的基本方法，數(shù)值實驗結果表明，LINGO軟件在求解該類問題中所花費的時間短且精確度高的優(yōu)點，因此，高中數(shù)學建模愛好者可以將其應用于求解數(shù)學建模中的優(yōu)化問題。

關鍵詞：LINGO軟件；數(shù)學建模；線性規(guī)劃

一、國內(nèi)外高中數(shù)學建模的進展

美國教師聯(lián)合會在《中學數(shù)學課程和教學評估標準》中最早提出了高中數(shù)學建模。目前，國外高中數(shù)學建模競賽主要有美國高中數(shù)學建模競賽，該項競賽是結合中學生所具有的特點進行設計的，競賽隊通常是由４名學生，外加一名指導教師組成，時間多數(shù)在每年１１月第一周的星期五開始，由參賽隊從當年所給出的兩個實際問題中任選一個完成。荷蘭從１９９０年開始至今，每年舉辦一次稱之為Ａ－ｌｙｍｐｉａｄ的數(shù)學比賽來促進中學數(shù)學教育中應用數(shù)學的發(fā)展。為進一步普及數(shù)學建模教育，增強中學生的數(shù)學核心素養(yǎng)，美國數(shù)學及其應用聯(lián)合會聯(lián)合香港儒蓮教科文機構于２０１４年創(chuàng)辦了國際數(shù)學建模挑戰(zhàn)賽，旨在鼓勵各國的高中生積極主動地應用數(shù)學知識解決現(xiàn)實中的一些問題。

我國中學數(shù)學建模起源于１９９１年１０月上海市舉辦的“金橋杯”中學生數(shù)學應用知識競賽，在此影響和啟發(fā)下，北京市從１９９３年開始舉辦同類型的中學生數(shù)學知識應用競賽。為進一步改善我國基礎數(shù)學教育的應用不足，普通高中數(shù)學課程標準《（實驗）》（２００３年版）提出，“高中數(shù)學課程應當提供一些基本內(nèi)容的實際背景，以便更好地反映數(shù)學的應用價值，開展一些‘數(shù)學建模活動”。而隨著我國的《普通高中數(shù)學課程標準（２０１７年版）》的頒布，已經(jīng)非常明確地指出“數(shù)學建模”是高中數(shù)學的六大核心素養(yǎng)之一，并且將數(shù)學建模與數(shù)學探究活動作為主線之一。為更好地銜接高中數(shù)學與大學數(shù)學，提升高中生的團隊合作方式解決現(xiàn)實問題的綜合和創(chuàng)新能力，激發(fā)他們的應用數(shù)學的興趣，并為國內(nèi)外一流名校選拔數(shù)學專業(yè)有較大潛力的人才，清華大學聯(lián)合中國工業(yè)與應用數(shù)學學會于２０１５年創(chuàng)辦了“登峰杯”全國中學生數(shù)學建模競賽，該項競賽主要目的是考查參賽者如何將實際問題轉(zhuǎn)化成數(shù)學模型、并借助于計算機通過編程求解數(shù)學模型的能力以及論文寫作方面的能力。

二、優(yōu)化問題與ＬＩＮＧＯ軟件

人們在現(xiàn)實的生活、科學研究和生產(chǎn)等問題中經(jīng)常需要從眾多可行的方案中選擇出最好的方案，比如，在生產(chǎn)計劃中，如何做到既能提高產(chǎn)值，又能使獲利最大；在資源的分配問題中，如何分配既能保證各方面的要求得到滿足，又能使經(jīng)濟效益最大；在經(jīng)濟管理問題中如何做到使單位成本的產(chǎn)值最大或盈利最大等，一般把這類問題被稱為最優(yōu)化問題。

其一般描述為minf（x）

s.t.g（x）≤0? i=1，2，3，…，mh（x）=0? ?j=1，2，3，…，l? （1.1）

其中f（x）∶Rn→R為目標函數(shù)，gi（x）∶Rn→R為約束函數(shù)。因為max｛f（x）∶x∈S｝=-max｛-f（x）∶x∈S｝且gi（x）≥0=-gi（x）≤0。故求解最大值問題都可以轉(zhuǎn)換為最小值問題。

當問題（１．１）滿足所有的變量是連續(xù)的、目標函數(shù)又是單目標且f（x）和gi（x）均是線性函數(shù)，則該問題就稱之為線性規(guī)劃問題，其求解通常是先寫出滿足題設的目標函數(shù)和約束條件；再根據(jù)約束條件進一步確定可行域；最后，求出目標函數(shù)在可行域內(nèi)的最優(yōu)解和最優(yōu)值。但在實際問題中，當遇到的變量和約束條件都較多時，僅憑這樣的求解方法則很難以得出最優(yōu)解。當問題（１．１）中一部分變量取整數(shù)，另一部分取為實數(shù)就稱之為混合整數(shù)規(guī)劃問題；當變量都取為整數(shù)就叫整數(shù)規(guī)劃問題；特別是變量只取整數(shù) 或 時，將此稱為０－１規(guī)劃問題。

０－１規(guī)劃問題也是高中數(shù)學建模競賽中經(jīng)常會遇到的問題，因該問題對現(xiàn)實生活、生產(chǎn)有著重要的意義，它已被廣泛地應用于航班安排、人力資源分配和背包問題等。其求解方法除了分支定界法、動態(tài)規(guī)劃法和罰函數(shù)法等傳統(tǒng)算法外，還有元胞蝙蝠算法、蜂群算法和粒子群優(yōu)化算法等新型智能優(yōu)化算法。但這些算法對高中生而言，相當抽象，所以就很難理解，而求解這類問題就可以用運籌學中一款簡單、易于操作的數(shù)學軟件－ＬＩＮＧＯ來實現(xiàn)。

ＬＩＮＧＯ軟件是由美國的ＬＩＮＤＯ系統(tǒng)公司開發(fā)的一套專門用于求解規(guī)劃問題和方程組問題的數(shù)學軟件。該軟件的優(yōu)勢不僅在于可以求解整數(shù)規(guī)劃問題，而且程序編寫簡單、運行速度快。基于此，該軟件已被越來越多的學者應用于求解交通運輸，投資與決策，成本預算以及人力資源分配等各類優(yōu)化問題。運用ＬＩＮＧＯ軟件求解優(yōu)化問題的方案通常是先結合所研究的實際問題，建立起數(shù)學模型，再對模型進行求解。

三、應用案例

案例１：農(nóng)場作物種植問題

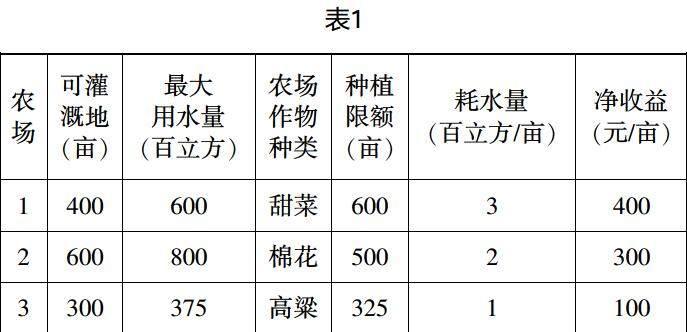
假設某一地區(qū)的一條灌渠可同時供就近的三個農(nóng)場使用，各農(nóng)場都可以種植甜菜、棉花和高粱三種作物，已知各農(nóng)場的可灌溉地、分配到的最大用水量、各種作物的用水量、凈收益及國家規(guī)定的該地區(qū)各種作物種植總面積最高限額如下表１所示：

三個農(nóng)場達成協(xié)議，他們的播種面積與其可灌溉面積相等，在上述限制條件下，如何制定各農(nóng)場種植計劃使本地區(qū)的三個農(nóng)場的總凈收益最大。

分析：不妨用x1，y1，z1，x2，y2，z2，x3，y3，z3分別來表示農(nóng)場１、農(nóng)場２和農(nóng)場３各自種植的甜菜、棉花和高粱的畝數(shù)，依據(jù)題意建立的模型如下：

Max=400（x1+x2+x3）+300（y1+y2+y3）+100（z1+z2+z3）

s.t.x1+x2+x3≤600y1+y2+y3≤500z1+z2+z3≤325x1+y1+z1≤400x2+y2+z2≤600x3+y3+z3≤3003x1+2y1+z1≤6003x2+2y2+z2≤8003x3+2y3+z3≤375x1，y1，z1，x2，y2，z2，x3，y3，z3≥0

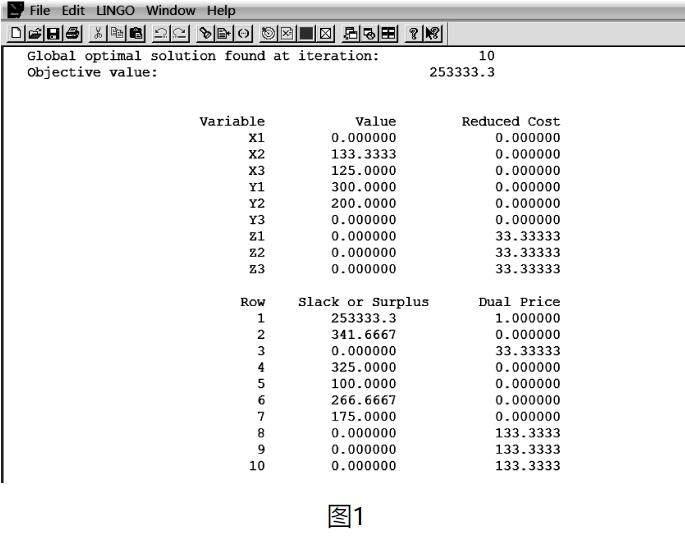
利用ＬＩＮＧＯ軟件求解程序如下：

ＭＯＤＥＬ：

max=400*（x1+x2+x3）+300*（y1+y2+y3）+100*（z1+z2+z3）;

x1+x2+x3<=600;

y1+y2+y3<=500;

z1+z2+z3<=325;

x1+y1+z1<=400;

x2+y2+z2<=600;

x3+y3+z3<=300;

3*x1+2*y1+z1<=600;

3*x2+2*y2+z2<=800;

3*x3+2*y3+z3<=375;

ＥＮＤ

由此可知，最大總凈收益為２５３３３３．３元。

案例２：選課策略問題

某大學數(shù)學與統(tǒng)計學院在運籌學專業(yè)的大學一年級新生中開設以下課程，如表２所示：

學院規(guī)定，大一年級的學生在學期末至少選兩門計算機課、兩門數(shù)學課和三門運籌學課，為了選修課程門數(shù)最少，應學習哪些課程？

該問題的數(shù)學模型：xi=1? 選中課號為i的課0? 未選中

Min=x1+x2+x3+x4+x5+x6+x7+x8+x9

利用ＬＩＮＧＯ軟件求解程序如下：

min=x1+x2+x3+x4+x5+x6+x7+x8+x9;

x1+x2+x3+x4+x5>=2;

x3+x5+x6+x8+x9>=3;

x4+x6+x7+x9>=2;

2*x3-x1-x2<=0;

x4-x7<=0;

2*x5-x1-x2<=0;

x6-x7<=0;

x8-x5<=0;

2*x9-x1-x2<=0;

@bin（x1）;@bin（x2）;@bin（x3）;@bin（x4）;@bin（x5）;@bin（x6）;@bin（x7）;@bin（x9）;

END

因此，該專業(yè)學生至少選修６門課程，學習微積分、計算機模擬、計算機編程、數(shù)學實驗課程、線性代數(shù)和應用統(tǒng)計。

該文研究了ＬＩＮＧＯ軟件求解農(nóng)作物種植計劃和大學生選課這兩個優(yōu)化問題的基本方法，從程序運行時間和數(shù)值結果可看出，ＬＩＮＧＯ軟件求解此類問題的速度和精確性較傳統(tǒng)算法有顯著的優(yōu)勢。因此，一線數(shù)學建模指導教師在數(shù)學建模培訓中可以將ＬＩＮＧＯ軟件作為培訓的數(shù)學軟件之一。

參考文獻：

［１］中華人民共和國教育部． 普通高中數(shù)學課程標準（實驗）［Ｍ］． 北京：北京師范大學出版社，２００３．

［２］中華人民共和國教育部． 普通高中數(shù)學課程標準（２０１７年版）［Ｍ］． 北京：人民教育出版社，２０１７．

［３］唐加冕，周京徽． 線性規(guī)劃問題在經(jīng)濟生活中的應用［Ｊ］． 商業(yè)時代，２０１１（１９）：１０－１１．

［４］陳寶林． 最優(yōu)化理論與算法［Ｍ］． 北京：清華大學出版社，２００５．

［５］朱光軍，譚潔群，王云． 線性規(guī)劃在數(shù)學建模競賽中的應用［Ｊ］． 廣西大學學報（自然科學版），２００８，３３（１２）：２２６－２２９．

［６］王熙照，賀毅朝． 求解背包問題的演化算法［Ｊ］． 軟件學報，２０１７，１（０１）：１－１６．

［７］李枝勇，馬良，張惠珍． ０－１規(guī)劃問題的元胞蝙蝠算法［Ｊ］． 計算機應用研究，２０１３，３０（１０）：２９０３－２９０６．

［８］謝金星，薛毅． 優(yōu)化建模與ＬＩＮＧＯ軟件［Ｍ］． 北京：清華大學出版社，２００６．

（責任編輯：莫唯然）