順逆共生：我的數學教學之道

摘 要：學生的數學學習是在“順逆共生”中不斷前行、深入的過程，其間有經驗的對接和沖突、求知過程中的“順境”和“逆境”，也有知識的建構和解構、局部化和整體化，以及思維的正向與逆向、聚合與發散等。課堂上，加強“順”與“逆”的對接，把握“順”與“逆”的坡度，調控“順”與“逆”的節奏，讓學生積累豐富的數學經驗，形成結構化的知識體系，淬煉靈動深入的思維，最終指向學科素養的培育。

關鍵詞：順逆共生；經驗；結構；思維；坡度

一、“順逆共生”的提出

初為人師時，辦公室窗前有一棵銀杏樹，歷經數十年風雨仍枝繁葉茂。我常常凝望著它，它伴隨我走過了工作初期的迷茫。而后的歲月里，雖然工作地點變動多次，但這棵樹仍給予我思想的養分，改革的勇氣。

開始時，我想讓自己長成一棵樹，讓學生在我的樹蔭下成長。在課堂上，我會考慮到每一個學生有可能產生的困惑，然后做足知識的鋪墊，搭好上行的階梯。如教學“9加幾”時，先進行三個層次的課前練習，第一層次進行“4=1+（ ）”這類練習，第二層次進行“10+3”這類練習，第三層次進行“9+1+2”這類練習，通過以上練習，學生就能夠更順利地研究出“9加幾”的計算方法。基于這樣比較扎實的鋪墊，學生學起新知來，自然能夠輕松不少，這不禁令我沾沾自喜。但在一次調研考試中我發現：面對一道平時沒有做過的題目，我們班的正確率明顯低于其他班級。為什么會這樣？我開始不斷地追問自己。

當我陷入迷惘，又想起窗前的那棵樹，在共同的生命季候中，年復一年，樹木經歷著發芽、開花、葉落、枝枯，經歷著陽光沐浴、風雨洗禮，經歷著順境與逆境，既向上長葉，也向下扎根。學生的學習也應該這樣，如果教學過程中的課前鋪墊過多、探索步驟過碎，學習過程看起來順暢了、輕松了，但實際上課堂是單向的、封閉的，剝奪了學生本該自己經歷的思維過程。學生獨自經歷完整的、有順有逆的知識探索過程，也許會成長得很慢，會有些艱難，但是這樣的學習才具有挑戰性，習得的知識才有生命力。

二十余年來，經過不斷地實踐和反思，我對數學學習過程的認識愈發清晰。其實，數學學習的過程曲折復雜，除了前述學習經歷中常出現的“順境”“逆境”，在數學學習的經驗、知識、思維等方面都普遍存在“順逆”雙向性，只有引導學生正確面對并有效處理真實的“順逆共生”現象，才能更好地開展數學學習。

二、“順逆共生”的內涵闡釋

（一）經驗的順逆共生

1.經驗的對接與沖突

數學學習過程中，學生已有的各種經驗有時能對接新知，在經驗的對接過程中自然產生新知，但有時也會與新知產生沖突，引發內心一時的矛盾。無論是經驗的順利對接還是矛盾沖突，最終都會實現經驗的自然生長。如學習“認識分米和毫米”前，學生對分米的認識并不完全為零。課堂上，先讓學生在臺階上把已經認識的3個長度單位排隊。一開始，學生對接已有經驗，自然想到根據樓梯的樣子從低到高把三個長度單位逐級排隊（如圖1），但他們注意到每級臺階的高度相等，而毫米與厘米之間的進率是10，厘米與米之間的進率是100，長度單位之間的關系與臺階高度的關系不吻合，由此認知沖突引發學生思考：如果這兩種關系要吻合。則需要把第三級臺階空出來，把“米”放在第四級臺階（如圖2），為在第三級臺階上創造出一個新的長度單位提供了可能。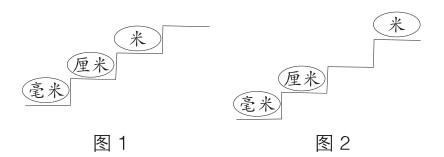

2.經歷的“順境”與“逆境”

學習經驗的積累需要經歷知識的產生過程、完善過程，其中的磕磕碰碰、曲曲折折，對于知識本身來說沒有意義，但是對于學習者來說，是一條積累新知學習經驗、產生深度理解的路徑。課堂中，教師還需給予學生一定的挑戰性任務，讓學生常經歷逆境，此間有時會出現暫時性后退的現象，實屬自然。要讓學生接受多元“考驗”，增添突破逆境的經驗，從而在今后的學習中走上更順的路。例如，教學“9加幾”，須要讓學生掌握“湊十法”，將不熟悉的計算轉化成為熟悉的計算，這對初學進位加法的一年級學生是有挑戰性的。在學習“湊十法”之前，學生對“9+3”這樣的算式往往有自己的計算方法，比如從9往后數3個數。當學生剛剛使用“湊十法”將新知轉化成舊知時，計算的正確率也許會出現暫時性下降，但這只是只暫時的、表面的現象。實際上，學生正由一開始的數數計算轉向運用轉化方法計算，能根據這種轉化的方法得出8加幾，7加幾等其他算式的計算方法，并進一步延伸到其他的計算。在此學習過程中，學生面對新算法的新經驗正在不斷生成，克服逆境的經驗也在不斷積累，變成后繼學習的寶貴經驗財富。

（二）知識結構的順逆共生

1.知識的建構和解構

知識的建構指新舊知識相互聯系、反復作用，形成意義、組建和調整知識結構的過程。知識的解構是指打破原有的知識結構，再進行重新整合。陳葆在《解構主義與建構主義的異質同一性》一文中指出：“從概念上看，解構主義理論強調在固有思維模式基礎上的‘破壞和‘粉碎；建構主義理論強調在原有認知基礎上的‘重新建構。從形式上看，一個是將‘已形成的思維整體分解成‘碎片，再進行創新性的‘整合。一個是將吸收的新信息與頭腦中現存的經驗‘同化、順應和平衡形成‘新的認知。”雖然建構和解構看起來是一對“立”和“破”的矛盾體，但是在知識學習的過程中，面對同樣的內容，無論是分解再整合，還是基于原有認知的重新建構，都產生于內在的不斷沖突與調和，從而形成新的認識的循環往復的過程。例如，教學“整數乘法”時，教師引導學生基于加法的結構，自主建構出乘法的意義：幾個相同的數相加。這樣，在教學“整數乘分數”時，教師就可以引導學生基于整數乘法的意義，自主建構出表示“量”的分數與整數相乘的意義，從中揭示出分數乘法的第一種意義：求幾個相同分數的和。還要超越學生原有的認知結構，教學表示“率”的分數與整數相乘時，揭示分數乘法的第二種意義：表示一個數的幾分之幾是多少。進一步拓寬原有的對“求一個數的幾分之幾是多少”的認識，理解求一個數的幾分之幾不僅可以利用“先除再乘”的方法去解決，還可以利用分數乘法去解決。這一過程，即對原有的認知進行解構，生長整合出新的理解，進而解決基于這兩層意義生成的新問題。

2.知識的局部和整體

知識的發生、發展伴隨著順逆關系：一方面要從知識點的學習到建立其間的聯系，從局部結構的構建到整體結構的形成，讓學生既見樹木又見森林；另一方面也要引導學生從整體結構的視角把握局部結構，居高臨下地認識各知識點或知識塊的意義和價值，從統一的觀點理解已學的零散知識。如教學“平面圖形的面積”時，由長方形的面積公式推導出正方形和平行四邊形的面積公式，再由平行四邊形的面積公式推導出三角形和梯形的面積公式，這是局部結構的自然生成。而后，通過回溯教學，引導學生從梯形面積公式的視角回看三角形、平行四邊形、長方形和正方形的面積公式。回過頭來重新理解這些平面圖形面積公式與梯形面積公式之間的關聯，從而發現梯形的面積公式是一個通用公式，并進一步聯系到數與代數領域中求等差數列之和也可以類比使用梯形的面積公式，將數與形結合，這是知識整體結構觀的體現。從局部結構到整體結構，從順向延伸到回溯性學習，打通了同一領域知識間、不同領域知識間的關聯，完善了學生的認知結構，在順遞共生中形成對數學知識的整體理解。

（三）思維的順逆共生

1.思維的正向與逆向

思維的方向性決定了思維過程常有與之相反的思維過程。如，加和減的互逆，乘和除的互逆，整數的乘法和因數分解，舉出正反例，公式的正向、逆向應用，分析與綜合，抽象化與具體化等，都是思維的正向與逆向的具體體現。數學學習正是在“正逆”思維的循環往復中從淺表走向深入，正逆向思維相輔相成，缺一不可，讓學生全方位、多角度地分析問題，有助于推動學生思維的發展。例如，教學“公因數與最大公因數”時，前面的學習過程中，都是先找到了兩個數的公因數，再從公因數中去尋找兩個數的最大公因數。接著可以引導學生逆向思考：能不能根據兩個數的最大公因數，想到它們所有的公因數呢？引發學生根據公因數和因數的關系，先找到最大公因數，然后找公因數，并且利用分解質因數的知識以及數與數組合的知識去理解其中的道理。這里運用正向和逆向兩種思維，學生可由此體會到數學知識之間的相互關聯。

2.思維的聚合和發散

聚合思維將所有思考集中于一點，發散思維則是從一點出發，沿多個方向或路徑達到思維目標。抽象化、一般化、形式化以及邏輯推理，多屬于聚合思維，而具體化、形象化以及聯想、類比、想象等，多屬于發散思維。數學思維需要綜合地運用聚合思維和發散思維這兩種總體上互為順逆的思維方式，才能有效地解決問題，增進知識理解，提高思維的深刻性、廣闊性。如計算新授課的教學，應著重鼓勵學生結合對數的認知經驗、對生活中數量關系的了解以及相關的計算經驗，借助直觀圖形、計算工具、聯想類比等，開展計算實驗，放飛思維，從多種途徑積極探索有效的計算方法，同時也要理解同伴的探索過程，進行交流比較，這是思維發散的過程。然后，在此基礎上及時反思總結，找出最佳計算方法，揭示計算規律、本質和原理，并及時提煉數學方法，積累探索算法的經驗，這是思維聚合的過程。數學學習也正是在“聚合和發散”的思維交融中從單一到多元再到優化，助力學生思維的發展。

三、“順逆共生”的教學實施

行走不止，思考不息。“順逆共生”既然在數學學習過程中如此普遍地存在，處理好“順逆共生”對學生積累經驗、探索知識、發展思維具有積極有效的作用，那在數學教學中可以從哪些方面具體實施呢？

（一）加強“順”與“逆”的對接

“順”與“逆”是對立統一的關系，數學學習中的“順”與“逆”相反相成，兩者之間也存在共生的關系，需要做好對接。

例如，抽象與具體是一對順逆關系，屬于聚合思維與發散思維的關系。兒童，尤其是低年級兒童是感性的精靈，其思維以具體的感性思維為主，而數學思維以抽象的理性思維為主，教學中應將抽象與具體相對接。一方面，要將理性的知識用感性的形式來表達，將抽象的知識具體化、形象化；另一方面，要助力學生逐漸從具體的感性思維過渡到抽象的理性思維，經歷數學化（如抽象概括、符號化）的過程。如此，從具體到抽象再到具體，讓學生經歷多次順逆對接過程，可以讓學生內在的理性精神得以萌發。

又如，運算中的加法和減法、乘法和除法，是兩對順逆關系。減法、除法源自加法、乘法，前者與后者的教學過程中，需要處理好兩者的對接關系。以思考、計算5-3為例，“5-3=？”相當于求“3+？=5”，這就需要基于加減法的順逆關系，將加法和減法進行有效對接、過渡。教學時，從學生熟悉的加法情境引入，再創設減法情境，使學生想到可以依據先前經驗列出加法算式。在此基礎上，讓學生體會形如“3+？=5”的加法也可以用減法來表示。然后結合具體背景說出算式的含義，感悟減法的含義，最后讓學生經歷多情境多層次的練習，引導學生進一步理解減法算式中各個量的含義，了解加法和減法之間的關系。

（二）把握“順”與“逆”的坡度

知識的學習要有一定的思維含量，要有適當的挑戰性，知識的生成和發展過程，常需逆勢而上、逆向思維，以此促進學生思維的進階。在一組“正向、逆向思維”中，往往“逆向思維”較難。因此，教學中需要處理好思維的正向與逆向、聚合與發散之間的關系，把握好“順”與“逆”的坡度。

比如，教學“兩步連乘解決實際問題”，學生根據條件提出兩步連乘的問題之后，可再要求學生倒過來，根據問題補充相應的條件，使之能用兩步連乘來解決。從由條件想問題到由問題想條件，對學生來說，無疑是一個挑戰，而我們出示的問題直接決定了學生是否能夠達成思維的生長。比較以下幾個問題：（1）3只燕子4天吃多少只害蟲？（2）燕子一共吃了多少只害蟲？（3）3只燕子一共吃了多少只害蟲？分別讓學生補充條件。很顯然，如果出示問題（1），學生會補充“1只燕子1天吃多少只”這個條件，思維顯得過于單一和封閉。如果出示問題（2），學生會陷入毫無頭緒的處境，思維顯得過于開放。而如果出示問題（3），學生的思考不僅有了范圍，而且能在這個范圍內提出多樣化的條件，這樣的問題才是比較適切的。因此，從“順”到“逆”的過程中，坡度太緩，學生會索然無味；坡度太陡，學生會望而生畏。只有設好適當的坡度，“讓學生跳一跳能夠得著”，才能促使學生思維不斷向高處攀爬。

（三）調控“順”與“逆”的節奏

著眼于具體的一堂課的教學，應當是有順有逆，如此才能有課堂節奏的變化，課堂才有張有弛。正如馮衛東老師說的那樣：“在‘順的時候，學生思維涌動、對話踴躍，課堂流程推進速度較快。在‘不順的時候，學生苦思冥想、糾結焦灼，教學行進放緩。在波動的變化中，學生既能體會‘勝任挑戰的欣悅，從而信心再增；也會品悟戰勝困難的艱辛，從而意志彌堅。”

著眼于整個數學知識體系，知識并不是勻速生長的，有時需要在“順向”知識處逗留一段時日，再教學“逆向”知識，有時則需要教完“順向”知識后即刻教學“逆向”知識。如學完整數乘法后，并未即刻教學整數除法，而是給了學生充分內化吸收“順向”知識的時間，做好乘除法“順逆對接”的準備、過渡。而學完長方形的面積公式以后，就緊接著進行已知面積和長，計算寬是多少等逆向的應用。知識體系中“順”和“逆”節奏的調控源自學生對“順向”知識的接受度。接受度高則節奏放快，接受度低則節奏放緩。

我期待，順逆共生的課堂能在適切的坡度、適宜的節奏中讓學生經歷學習的起伏、思維的波折，從而打通“順”與“逆”的關聯。讓學生在順逆共生的學習過程中，積累豐富的數學經驗，形成結構化的知識體系，淬煉靈動深入的思維，最終形成良好的數學素養。

參考文獻：

[1]陳葆.解構主義與建構主義的異質同一性.[J].教學與管理，2007（12）.

[2]馮衛東.“不太順”的課也許才是真正的好課.[J].初中生世界，2014（16）.

（陳晶，江蘇省南通市崇川小學，郵編：226014）