辨明真假，培養數據意識

《義務教育數學課程標準（2022年版）》指出，“數據意識”是小學階段學生核心素養的主要表現之一。隨著科技迅速發展和大數據時代的到來，從小培養學生的數據意識顯得尤為重要。數據意識有助于學生理解生活中的隨機現象，逐步養成用數據說話的習慣。教學時可以設計一些生活中與隨機現象和數據分析有關的數學問題，通過問題解決，引導學生正確認識、精準分析和準確表達數據，培養學生的數據意識。

【題目】

中央電視臺曾經有一檔電視節目《是真的嗎》，節目根據網友提出的問題，通過各大新媒體共同互動求證，運用調查、實驗、觀察、推理、計算、分析等手段，一起探求真相。下面讓我們來參加一場數學版的“是真的嗎”活動吧。

第1題 哪組均分高？

某次數學期末考試中一組和二組男、女生平均分如表1所示（設每位學生的分數只能是整數或小數部分為0.5的小數）。根據表格中的數據可知，一組男生的均分比二組男生均分高，一組女生的均分也比二組女生均分高，所以一組學生的均分比二組學生的均分高。這是真的嗎？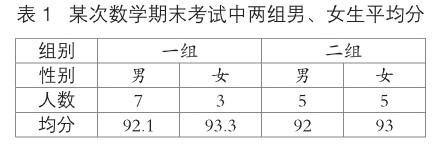

第2題 誰的進步大？

小麗和小敏最近勤加苦練跳繩，都取得了一定的進步，圖1、圖2是根據兩人最近5次1分鐘跳繩成績畫出的折線。已知第1次小麗跳120個，小敏跳123個。從兩條折線可以看出，小敏進步比較明顯，所以她的進步更大。這是真的嗎？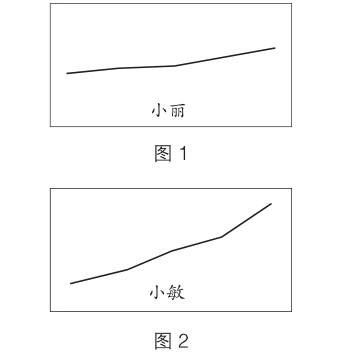

第3題 誰是專業籃球運動員？

A、B、C三人中有1人是專業籃球運動員，A的投籃命中率為50%，B的投籃命中率為60%，C的投籃命中率為54.5%。因為60%>54.5%>50%，所以B的投籃水平最高，專業籃球運動員應為B。這是真的嗎？

【解析】

第1題，由于一組的男女生均分都比二組高，學生易認為一組的整體均分也比二組高，也有學生會發現兩個組男女生人數不同，可能問題沒那么簡單，于是嘗試從計算的角度進行驗證。一組：（92.1×7 + 93.3×3）÷（7+3）=（644.7+279.9）÷10=924.6÷10=92.46；二組：（92×5+93×5）÷（5+5）=（460+465）÷10=925÷10=92.5。計算的結果顯示二組的平均分更高一些。還有的學生發現問題后將每個人的分數列出來比較總數，得出二組的總分比一組高0.4分，因此平均分高0.04分。不論是直接計算還是列出每個人的得分后再算，都得到同樣的結論，那就是二組的均分比一組要高。事實真的是這樣嗎？

第2題，學生學習折線統計圖時，都知道折線統計圖既能表示數量的多少，又能清晰地反映數量增減變化的情況。看到坡度平緩就想到數據變化較小，坡度較陡就想到數據變化較大。當第一眼看到題目所給的兩條折線時，容易根據折線的變化幅度認為小敏跳繩增長較快，進步較大。事實真的是這樣嗎？其實，要想將兩人的數據通過折線圖進行比較，就得將其折線圖置于坐標系中，并統一縱軸單位長度和起始數據值，形成規范、準確的折線統計圖，否則無法比較兩組數據。而原圖只給出兩條折線，根本無法表示每組數據的大小、變化快慢，容易產生錯覺，導致誤判。事實上，根據小麗和小敏最近5次跳繩的成績，在Excel表中分別生成兩幅折線統計圖（如圖3、圖4），從中可清楚地看出小麗進步更大。所以原來的說法是假的。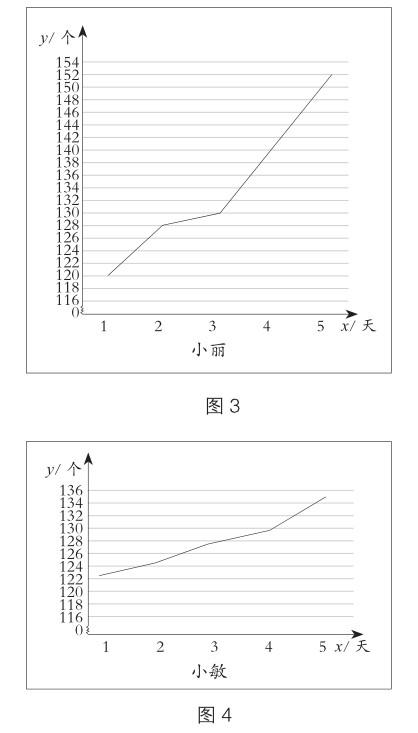

第3題，投籃命中率反映投中次數與投籃次數的關系。學生需要有這樣的基本認識，即只有收集了足夠多的數據，才能得到比較穩定可靠的命中率。表2是三人投籃的原始數據，從中可以看出，A和B只投了幾次，如果再進行一次投籃活動，A和B的命中率還能分別達到50%和60%嗎？不一定。C正是NBA球員庫里，據統計，庫里在11年的NBA生涯中共參賽527場，投籃4734次，命中2578次，命中率為54.5%。C的投籃命中率相當高，而且是通過大量數據計算所得，穩定性、可信度高。可見，C才是專業籃球運動員。所以“專業籃球運動員應為B”這一說法是假的。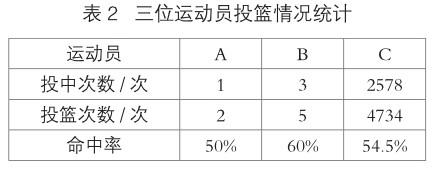

【設計意圖】

一、追根溯源，正確認識數據

面對數據，我們不能不假思索地直接使用，而要保持清醒的思考與判斷，其中首要的是追根溯源，正確認識數據。三道題都聚焦實際問題，試圖用數據說話，面對題目給出的數據，學生需要思考這些數據是如何得到的，正確認識平均數、百分數等統計量的意義。例如，第3題主要考查學生對投籃命中率這個統計量的意義理解。百分數是兩個數量倍數關系的表達，既可以表達確定數據（如利息、折扣等），也可以表達隨機數據（如某籃球運動員投籃命中率）。因為在隨機事件中，每次收集的數據可能不同，需要有足夠多的數據才能從中獲得穩定可靠的統計量，因此，我們需要追尋原始數據（若僅為理解統計概念，也可設置某些數據構建模型），如根據表2可以了解這三個投籃命中率的由來，讓學生從統計的角度想一想數據是否合理，能否從中作出正確的判斷。

二、深度思考，精準分析數據

生活在用數據說話的時代，除了正確認識數據，還需要我們具備以合理、專業的視角對數據進行解讀和分析的能力。平均數在數學中是一個常用的統計量，表示一組數據的集中趨勢。教學時教師通常注意到幫助學生感受平均數具有虛擬性、趨中性、敏感性等特征，但大都忽略了平均數還有近似特征，由此導致了誤差的產生，尤其是進行數據比較時可能出現錯誤的判斷。第1題中雖然一組的男、女生均分都比二組高，但通過計算發現二組的平均分更高一些。如果不考慮平均數的近似特征，分析到此戛然而止，就會產生誤判。因此，第1題的設計旨在引導學生在分析數據時要深度思考，全面考慮數據的相關特性，發現數據背后隱藏的信息，從而做到精準分析，并根據實際情況正確判斷。實際上，由于本題中一組男生和女生的平均數都是近似值，導致了一組總分的不確定，最終二組的平均分可能比一組高，也可能和一組相等，結論會出現反轉。

三、合理選擇，準確表達數據

由于統計圖既能直觀、形象地表示數據，又能以很小的篇幅給人們提供大量的信息，因此，統計圖已成為表現數據的主要形式之一，在報刊、網絡等媒體中經常出現。但如果這些數據的表達不恰當，例如在繪制統計圖的過程中故意夸大效果，歪曲事實，制造假象，則會導致人們的思考與實際情況發生偏差，使一些人上當受騙。第2題旨在考查學生對折線統計圖要素的理解和把握。圖1、圖2實際上是不完整、不規范的折線統計圖，縱軸起始數據和單位長度設置可能不一致，所反映出來的信息就會和實際完全不符，造成假象和錯判。一些商家會利用不規范的統計圖引誘消費者進行消費，例如一商品打折降價，從2800元降到2520元，如果將折線統計圖縱軸起始數據設為2500，單位長度設為25，就會呈現出降價幅度很大、價格已快要到底線的假象，事實上從2800元到2520元只下降了10%而已。這樣的問題可以幫助學生識別統計圖的真偽，體會準確表達數據的重要性，認識到在生動直觀地表示數據的同時，還要依據合理規范的圖表，才能作出正確判斷。

（劉艷，江蘇省南京市建鄴區教師發展中心，郵編：210017）