以學生為中心的高中數學課堂設計
——“直線與圓的位置關系”復習課

江蘇 段賽花

習總書記在黨的十九大明確提出加快建設創新型國家.本文以學生為中心設計高中數學課堂，嘗試讓學生站在系統高度上俯視數學，讓課堂更開放、更多元、更創新.以學生為中心的課堂設計采用“三看一注意”：一看，幾何問題代數化(解析幾何本質)；二看，幾何問題幾何化(看圖秒殺)；三看，幾何問題向量化(2008年引入教材)；一注意：數形一體，動靜結合.從一題多解到多題一解，始終以學生為中心展開變化.

筆者的課堂每一道題都有甲乙兩名學生與一名老師討論，解題應當自出機杼，想出自己的解法.首先，要不斷總結，琢磨已有解法，從細微處開始留心，看看能不能省去一兩步？能不能換一個角度？能不能將條件減弱或結論加強？很多時候，遞進式命題會拿去第一問，直接讓學生思考第二問，倘若學生毫無反應，再把第一問添加上去.整個習題解完以后一起回頭再看.變一變，編一編，解一解.最高境界，一堂課只解一道題，一道題包含整個單元知識.有時候循著學生的思路前進，得出新的解法，當然很好，如果走下去，發現此路不通，到不了目標，那也很好，知道了這條路走不通，不再堅持也是一種收獲.

筆者班級內有一個特別喜歡鉆牛角尖的學生，首先需要肯定他的想法，鼓勵他找到簡單而一般的解法，即使已有好的解法，也應注重研究其他思路：還可以從何入手？有哪幾個關鍵步驟？解決問題的辦法之一就是不斷變更問題，直到它變得容易處理.如若將結論當做已知，雖然原命題成立，逆命題不一定成立.但在有某種唯一性時，可以同時成立，這種方法是同一方法.有時候還會用原命題的等價條件逆否命題來研究問題，獲得一種嶄新境界.本文中的“秒殺”法在填空、選擇題中讓學生能夠高屋建瓴、一眼看穿.

一、課堂以學生為中心，如何選擇經典題

有效的數學教學需要學生積極地參與自己的學習過程，也就是要求學生扮演一個主動學習者的角色，通過事物的本質可以知道這在整個事件中的作用和運作規律.首先，教師要擔當學生數學學習促進者的角色，不斷激發學生與生俱來的自主數學學習的意識；其次，教師要促進學生自主“守法”“用法”“立法”，讓學生逐步形成“自適應”的數學學習策略與方法.選題要吻合“三看一注意”.

拋出問題：已知圓M:x2+(y-6)2=16,點P是直線l:x-2y=0上的一個動點,過點P作圓M的切線PA,PB,切點分別為A,B.

(2)若△PAM的外接圓為圓N,試問:當點P在直線l上運動時,圓N是否過定點?若過定點,求出所有的定點的坐標;若不過定點,說明理由;

(3)求線段AB長度的最小值.

解析：(1)學生1：由題意知,圓M的半徑r=4,圓心M(0,6),

∵PA是圓的一條切線,∴∠MAP=90°，

(2)學生2：圓N過定點.

設P(2a,a),∵∠MAP=90°,∴經過A,P,M三點的圓N以MP為直徑,

即x2+y2-6y+a(-2x-y+6)=0,

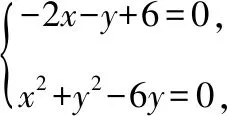
學生3：直徑式方程更快，從嚴謹性角度，需要用向量證明一下.

即x2+y2-2ax-ay-6y+6a=0 ①,

圓M:x2+(y-6)2=16,

即x2+y2-12y+20=0 ②,

②-①得2ax+(a-6)y+20-6a=0,

即為直線AB的方程.

學生5：等面積法

至此，初步達到“三看一注意”，學生的解法殊途同歸，都轉化為與|MP|有關的問題，實現兩個動點化歸為一個動點的問題，以靜制動.一題多解，為變題鋪墊，更為學生編題埋下伏筆.

二、課堂以學生為中心，如何建構深度學習

一是要強調過程性學習；二是要強調挑戰性學習；三是要強調創造性的學習.“數學教育是數學的再創造.”數學學習實際上是一種通過不斷質疑與探究，發現、理解、消化、應用、整合、創生新知的過程.

從變題開始，用“三看一注意”引導，實現多題歸一.

學生8：求切線長|AP|的最小值.

有學生9追問了為何不是求最大值.通過學生8的解答，恍然大悟.

學生10：求S四邊形AMBP的最小值.

因為學生9的追問，此處不再有學生提出求最大值的問題.

學生10說，是學生5給了他靈感.

學生11：求∠APB的最大值.

師：“你是怎么想到的？”

學生11展示點P在直線上的運動，看張角變化.先猜想再論證，把“三看一注意”的第二看演繹地很完美.解析幾何本質上還是幾何問題.

編題需要反復推敲，數字的設計，答案的美麗，知識點的融會貫通均需考慮在內.倘若學生能掌握“三看一注意”，能夠站在命題人的角度思考問題，一定能夠高屋建瓴，從系統的高度俯視數學.開放題的編題更具挑戰性，編一編，解一解，再修一修.遠離題海才能更勝一籌.把學生往前推，老師慢慢往后退，課堂是屬于學生的.

學生15：求直線AB過定點問題.他用兩圓方程相減得到直線AB方程，再轉化為恒成立問題.此處，教授“秒殺”方法，用類比推理.

問題由學生提出，教師需提升“三看一注意”的第一看，突出解析幾何的本質：幾何問題代數化.

三、課堂以學生為中心，如何注重知識的整體性與關聯性

利用“三看一注意”，以相關關系的視角審視數學知識的發展，以關聯的方式去學習，在似乎沒有關系的知識之間架起一座座橋梁，在相關性中拓展學生的思維，引導學生完整地經歷問題的提出和問題解決及數學思想方法的提煉和概括過程.

挑戰題：(2012·蘇州大學高考預測卷)若實數a,b,c成等差數列，點P(-1,0)在動直線ax+by+c=0上的射影為M，點N(3,3)，則線段MN長度的最大值是________.

傳統解法消參，找出定點A(1,-2)，尋找到AP為直徑的隱形圓，轉化為定點到圓上點的距離問題，找到圓心不動是關鍵，以靜制動.學生16從結構a-2b+c=0中比較直線方程直接看出定點A，值得肯定，這便是數學的直覺.進一步揭秘命題人的意圖，為他們自己編出高質量的習題埋下伏筆.幾何畫板的運用，提升學生深刻領悟“三看一注意”的注意：數形一體，動靜結合.

一節課的總結特別重要，圍繞點在圓上運動和點在直線上運動，從點到線再到面，拓展到兩圓問題，運動中蘊含不變，最后回歸到2019版人教版A選擇性必修第一冊99頁的15題：已知點P(-2,-3)和以點Q為圓心的圓(x-4)2+(y-2)2=9.

(1)畫出以PQ為直徑，點Q′為圓心的圓，再求出圓Q′的方程；

(2)設圓Q與圓Q′相交于A，B兩點，直線PA，PB是圓Q的切線嗎？為什么？

(3)求直線AB的方程

第三問中再試一次“秒殺法”，讓數學直覺來得更猛烈一些.學生編題不能全面總結，可以再添如下經典,

已知圓C:(x-1)2+y2=r2(r>0)與直線l:y=x+3.

(1)若直線l上有唯一的一個點P，使得過P點作圓C的兩條切線互相垂直，求r；

(2)若r=2，且直線l上存在點P，過點P作圓C的兩條切線夾角為60°，求點P的橫坐標.

答案：(1)2;(2)P(-3,0)或(1,4)

本節課緊緊圍繞“三看一注意”，激發了學生提出問題，研究問題的興趣.演繹數學本質：大膽猜想，小心求證.研究解析幾何最重要的方法是坐標法、綜合法、向量法.在千差萬別之中，存在著保持固定不變的形態的事項.抓住本質，就能以學生為中心設計出創新型的數學課堂.正如蘇東坡面對奔流不息的江水和永不休止的月亮圓缺交替變化，在《赤壁賦》中唱到：逝者如斯，而未嘗往也；盈虛者如彼，而卒莫消長也.宇宙萬物，若既從變化的方面去看它，同時又從不變的方面去看它，就會看到如蘇東坡所說的那種情形.從一方面去考查它，會看到它是瞬息萬變的，而若從另一方面去考查它，只會看到這種變化的內部，卻儼然存在萬世不變的實體.

老師眼中心中都要有學生，專業能力極強的老師，課堂設計特別完美，若一個人講得滔滔不絕，眼中能看到學生，但不太理會學生的思維，按照自己設計的程序行云流水，一氣呵成，這課是講給專家聽的，倘若來個外行呢？講得外行也明白，才是本事.淺入深出，層層遞進，等一等學生的靈魂.課堂的關鍵是學生領悟，哪個來聽課，都要初心不變.老師是為學生服務的，心中有學生，站在他們的角度，慢一點又何妨？學生想不出，等；學生算不出，等.學生的潛能無限.課堂上，等一等，就有很多新的發現；有學生想出各種解法，有學生計算卡住，點撥一下，老師幾乎不用講，學生興致勃勃來板演，問題就暴露出來了.