一種智能化排課算法的設計

張宗飛

（1.臺州職業技術學院信息技術工程學院，浙江臺州 318000；2.臺州中小企業信息化應用技術協同創新中心，浙江 臺州 318000）

排課是一個教學資源分配問題，由于各種教學資源在分配過程中的制約與沖突，使排課成為了多約束組合的優化問題[1-2]。

自從Gotlieb C C 在1962 年提出了排課問題的數學模型、Even S 等人在1976 年證明了排課問題屬于NP 完全問題之后[3-4]，對該問題的求解都集中在啟發式算法上，目標是在可接受的時間內搜索獲得最優的課表[5-8]。其中比較有代表性的是采用遺傳算法的解決方案，如文獻[5]從教室調度、沖突檢測和時間規劃3 個方面著手，使用遺傳算法設計了排課系統，實現了自動化排課；文獻[6]按照遺傳算法對排課問題編碼，并進行選擇、交叉操作，采用禁忌搜索算法進行變異操作，實現了比單純遺傳算法更優化的高校排課方案。對于排課問題，雖然采用遺傳算法已取得了一些比較好的成果，但是由于排課問題的復雜性和遺傳算法本身的缺陷，致使基于遺傳算法的求解始終無法達到解的下界，對最優課表的探索仍在進行。

量子進化算法(Quantum Evolutionary Algorithm，QEA)是一種新型的智能化啟發式算法[9-10]，自從提出之后就得到廣泛關注和不斷改進，在早熟收斂和全局尋優的平衡上優于其他啟發式算法，成為求解組合優化問題的一種通用計算框架[11-15]。

為此，該文使用QEA 來求解排課問題，通過設計一種基于QEA 的排課算法，實現自動排課功能。

1 排課問題模型構建

1.1 排課的沖突要素

該文將制約排課的5 種教學資源：班級、課程、教師、上課時間、教學場所稱之為排課的5 個沖突要素。為了合理解決排課過程中這5 個要素之間的沖突，將5個沖突要素進行分解，用相應的屬性來描述。

1）班級：班級編號、班級名稱、學生人數、所屬學院、所屬專業。

2）課程：課程編號、課程名稱、開課班級、任課教師、場所要求、周課時、起止周、課程性質、課程類型。

3）教師：教師編號、教師姓名、所屬學院、所屬專業、職稱。

4）教學場所：場所編號、場所類型、場所容量。

5）上課時間：用時間元來表示上課時間，每個時間元為2 課時。

1.2 排課的約束條件

排課過程中的約束條件可以分為硬約束和軟約束。

硬約束是指排課時不能違反的原則，用來約束排課方案的可行解。該文定義了如下4個硬約束條件：

1）一位教師在一個時間元最多只能安排一門課程，即：

2）一個班級在一個時間元最多只能安排一門課程，即：

3）一個教學場所在一個時間元最多只能安排一門課程，即：

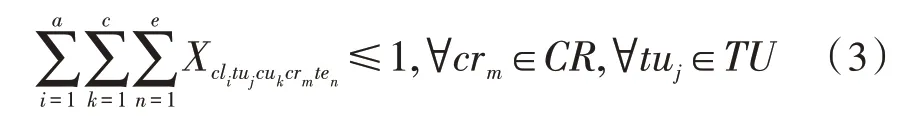
4）為課程cuk分配的教學場所crm可容納人數ym要大于等于上課班級cli的學生人數xi，即：

軟約束是指排課時人為的主觀要求，用來逼近排課方案的最優解，軟約束會因不同的要求而產生不同的約束條件。該文從時間元、班級課程分布、教師課程分布3 個指標要求來定義軟約束條件。

1）時間元指標要求：一個班級的課程要盡量安排在較好的時間元上。

2）班級課程分布指標要求：一個班級的同一課程如果在一周中有多個時間元則要盡量均勻安排。

3）教師課程分布指標要求：一個教師的任教課程如果在一周中有多個時間元則要盡量均勻安排。

針對上述3 個約束條件，對學生和教師展開調查，根據調查結果定義了對應的罰值表，如表1、表2、表3 所示。

表1 時間元評價罰值表

表2 班級課程分布評價罰值表

表3 教師課程分布評價罰值表

1.3 排課的數學模型

如果高校的班級數為i，一周的時間元數目為j，課程門數為k，教學場所數目為m，任課教師人數為n，則可以定義如下集合。

1）班級集合：CL={cl1,cl2,…,cli}，各班級的學生人數為{x1,x2,…,xi}

2）時間元集合：TU={tu1,tu2,…,tuj}

3）課程集合：CU={cu1,cu2,…,cuk}

4）教學場所集合：CR={cr1,cr2,…,crm}，各教學場所可容納的人數為{y1,y2,…,yd}

5）教師集合：TE={te1,te2,…,ten}

此時，排課問題的求解就是在滿足相應的約束條件下，尋找課程的如下映射關系：

2 基于QEA的排課算法設計

按照QEA 求解組合優化問題的步驟，設計基于QEA 的排課算法，記為TA-QEA。

2.1 量子染色體構造

根據課表的結構，以[班級*時間元]的向量矩陣形式來構造染色體，一個染色體表示一種排課方案。根據1.3 節對班級和時間元集合的定義可得到一個如式（5）結構的a行b列矩陣，每一行代表一個班級的課表。矩陣元素作為染色體的基因，由1.1 節所描述的班級、課程、教學場所、教師4 個排課要素構成，提取這4 個要素的編號屬性組成的向量按照式（6）結構進行編碼，一個屬性編號稱之為基因段，每個基因段與對應的排課要素關聯。

根據上述編碼，結合QEA 中量子染色體的結構，構造TA-QEA 的量子染色體結構如下：

2.2 種群初始化

首先，隨機生成一組如式（7）結構的量子染色體構成初始種群（n為種群的大小），然后，將染色體的各量子比特概率幅(αi,βi)初始化為。

2.3 種群觀測

對染色體的每一個量子比特進行測量，隨機產生[0,1]之間的一個常數r，若(αi為染色體第i個量子比特的概率幅)，則該量子比特(xi) 取1，否則取0。對量子態種群Q(t) 觀測后，就得到了觀測態種群其中，觀測態個體是長度為m的二進制串(x1x2…xm),xi∈{0,1}。

2.4 沖突檢測

觀測態種群中的個體就是TA-QEA 解空間中解的集合，一個個體代表一種排課方案，由1.2 節中的約束條件可知，這些個體都必須滿足硬約束條件，因此需要對觀測態種群中的各個體按照式（1）、（2）、（3）、（4）進行檢測，將不滿足這4 個約束條件的個體刪除。

2.5 適應度函數設計

分析1.2 節中的約束條件可知，硬約束是排課原則，算法中的每一個隨機解都要求必須滿足，而軟約束是排課方案的優化目標，最接近軟約束條件的解可視為最優解，因此排課問題的目標函數只需考慮軟約束。根據1.2 節中定義的軟約束條件設計TAQEA 適應度函數的步驟如下。

Step1 為軟約束指標分配權重得到排課的目標函數：

式中，δtu、δcl、δte分別為時間元評價罰值、班級課程分布評價罰值、教師課程分布評價罰值，ωtu、ωcl、ωte分別為對應評價罰值的權重。

Step2 采用比例放大方法將目標函數轉換成適應度函數：

式中，ρ為放大系數。

2.6 種群進化

種群進化包含染色體的更新和交叉過程[16]。染色體更新使用式（10）所示的量子旋轉門作為更新算子，按照式（11）所示將量子旋轉門作用于染色體的量子比特，使量子比特朝著目標方向偏轉，從而實現染色體的更新。

式中，θ為旋轉角度。

式中，θi=s(αi βi)·Δθi,Δθi、s(αi βi) 分別表示旋轉角的大小和方向，可以通過查表獲得。

為了維持種群的多樣性，避免算法陷入早熟收斂，需要對更新后的染色體進行交叉操作。為了減少沖突檢測的計算量，以矩陣的行為斷點進行全干擾交叉方式實現染色體的交叉操作。

2.7 循環停止設定

算法通過循環，使個體的適應度不斷增大，達到進化的目的。為了使算法能夠在可接受的時間內獲得滿意解，設置一個最大進化代數T作為TA-QEA的循環停止條件。

3 實驗驗證

3.1 實驗方案設計

實驗數據：實驗所用數據來源于某職業技術學院2019-2020 學年第一學期的開課任務表，共有學生9 871 人、開課教師521 人、班級249 個、開課課程984 門（同一門課程不同教師上課編號不同）、教學場所237 個，可安排的上課時間為星期一到星期五，每天8 課時（上午4 課時、下午4 課時），時間元為20 個。

實驗環境：為了驗證該文排課算法的性能，選取文獻[6]算法（記為TA-GA）作比較，兩者使用相同的染色體編碼方案和適應度評價函數。實驗在一臺Intel(R)Pentium(R)4 CPU 2.60 GHz、1.00 GB Memory、Microsoft Windows XP Professional SP2 OS 的單機上進行，在Eclipse 集成開發工具中使用Java 語言完成算法代碼。

實驗中各參數設置：種群大小n為200，最大進化代數T為1 000，排課軟約束指標的權重ωtu、ωcl、ωte分別為0.5、0.3、0.2，適應度函數的比例放大系數ρ為100。

3.2 實驗結果與分析

分別運行TA-QEA 和TA-GA 進行排課測試，以算法的優化能力和優化效率為評價指標，每進化100代記錄一次，實驗進行了10 次排課測試，TA-QEA 和TA-GA 均成功了8 次，分別取這8 次測試的平均值進行統計。算法優化能力的統計結果如圖1 所示，算法優化效率的統計結果如圖2 所示。

從圖1 數據可以看出，從第400 代開始，TA-QEA獲得的最優個體適應度值就超過了TA-GA，而且TAQEA 從第800 代開始最優個體適應度值就趨于穩定，先于TA-GA 100代左右。從圖2數據可以看出，在10次記錄點上，TA-QEA 的運行時間均要少于TA-GA，而且在進化后期，這種優勢更加明顯。分析圖1、圖2 的數據，可以得出結論：對于文中的排課問題，TA-QEA的尋優能力和尋優速度均優于TA-GA，表明TA-QEA在完成排課的質量和效率上都優于TA-GA。

圖1 算法優化能力的統計結果比較

圖2 算法優化效率的統計結果比較

4 結束語

針對高校排課工作的重要性與復雜性，將量子進化算法應用到排課問題中，使用優化的方法進行求解，在獲得可行課表后進一步優化逼近最優排課方案。實驗結果表明，該文算法能夠自動完成排課過程，排課的質量和效率都比較好。但是，算法生成的課表是在設置3 個軟約束條件下得到的滿意解，如果排課的人為要求更加復雜時，就可能需要對算法生成的課表進行人工修正。