木結構組合墻體自動裝配系統的研究

陶承宗，陳海衛,2*，陳延斌

（1.江南大學 機械工程學院，無錫 214122;2.江蘇省食品先進制造裝備技術重點實驗室，無錫 214122)

0 引言

近年來，隨著生活水平的提高及全球低碳環保理念的盛行，人們更加追求建筑材料的環保性和建筑物功能的多樣性[1]。現代木結構建筑憑借抗震性好，藝術表現性強，較其它建筑材料有噪音低，塵土少，廢水污染小等優點[2]，一直受到人們的關注。木結構組合墻體作為木建筑的主體，在載荷承受、防潮、保溫、隔音等方面有很高的要求[3]，因此生產商對墻體的生產加工裝配過程格外重視。目前，墻體生產過程存在自動化程度低、裝配路線規劃不合理的局面，亟需研制一款以裝配序列規劃為核心的自動化裝配系統去改善這樣的生產現狀。國內外在該領域有很多深刻的研究，美國VRCIM實驗室與美國NIST合作開發的虛擬裝配環境VADE[4]能自動從CAD系統中自動提取模型的幾何、物理屬性，通過戴頭盔人機交互的方式實現產品的自動裝配工藝規劃。秦鍇[5]利用拆卸法思想對裝配模型進行裝配序列規劃，用全回轉推進器的實例驗證了所開發裝配系統的有效性。張強[6]通過利用實時拆卸運動仿真跟實時干涉檢驗的方式求得裝配序列，成功實現HCW軋機的虛擬裝配。彭敏[7]利用SW的二次開發提取出裝配體模型矩陣信息，結合干涉矩陣的特性自動生成裝配順序，最后成功實現一級圓柱齒輪減速器的自動化裝配。Remeo M.Marian[8]等對改進型液壓直線電動機建立連接表，干涉表模型，利用GA算法對序列群優化，實現了電機的裝配工藝的改良。李慧[9]針對機器人自動化作業的需求，設計了機器人自動裝配系統，實現了產品的裝配信息建模、裝配序列規劃及裝配路徑規劃的功能。

本文針對墻體的生產裝配環節，首先設計了墻體的柔性裝配方案，之后對墻體模型進行底層分析和數字化建模，之后基于拆卸法思想進行墻體的裝配序列規劃；而后構建了基于機器人運動行程的評價指標數學模型，對序列群綜合評價篩選出了最優序列，使墻體的裝配任務得到了優化。

1 墻體模型的分析

本文研究的木結構組合墻體，主要是由托梁、底板、頂板、帶板、過梁等橫截面相同，長度不同的木板構成，如圖1(a)所示，零件木板沒有凹槽，卡口部件，采用的裝配方式是傳統的多塊木板的直接釘釘。根據墻體裝配圖以及墻體裝配的技術要求，由研究人員設計，得到如圖1(b)所示的墻體模型。

圖1 墻體組成零件及設計圖

墻體的裝配過程主要分為上料、運料、定位、裝配幾個環節，而系統主要由龍門機床、工業機器人，運料傳送帶、光纖傳感器、PLC控制器以及一些非標設備構成。首先搬運機器人將木板由載物臺運送到傳送帶，之后采用運料傳送帶實現木板運料，利用龍門平臺將木板零件運送到工作臺，利用三臺工業機器人跟龍門平臺配合完成整個打釘操作。裝配方案如圖2所示。

圖2 墻體的裝配系統圖

裝配系統建立之后，需要對墻體模型本身進行底層分析，采集出模型基本信息，從而為裝配工藝生成奠定基礎。對于給定的墻體模型，由于初始模型只是木板布局圖，并沒有給明打釘的情況，所以首要工作就是判定打釘的狀態，因兩板貼合是兩板可打釘的必要不充分條件，第一步也就是分析板與板的貼合狀態，從而初選出打釘位置。

對于兩面貼合，有如下充要條件：

1）面與面的距離為0，即兩面重合；

2）實體中面與面的外法向量方向相反，或者面與面的不包含邊界的矩形區域存在交集；

本文采用重合跟面面區域存在交集的方法判斷貼合。設存在面S1與S2，它們位于XOY平面且位于不同的部件：

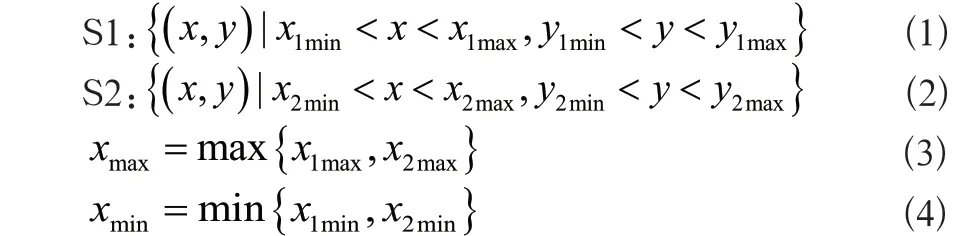
ymin跟ymax定義類似x，則兩面貼合的充要條件為：

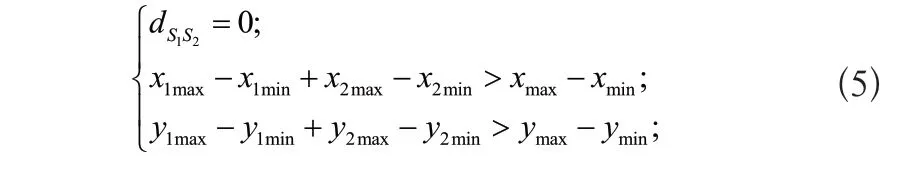
通過solidworks的API進行二次開發，完成裝配體信息的提取。利用Feature：：FirstFeature()和Featu -re：：GetNextFeature()按特征樹順序遍歷零件，通過Component2：：GetBodies2獲取對象的實體，再通過實體跟Face2：：GetFaces()獲得所有面信息，利用Assem -blyDoc：：ClosestDistance篩選出不可能貼合的部件，利用Measure：：NormalDistance測量面面距，結合Measure：：IsPerpendicular進行篩選出垂直面，再通過Face2：：GetEdges()獲得面的邊信息，通過邊信息跟Edge：：IgetStartVertex()就可以獲得邊的起始向量信息，通過Vertex：：GetPoint()獲取局部坐標系下的點坐標，再通過 MathPoint：：MultiplyTransform的方法去實現變換，從而轉換成全局坐標系下的坐標，進行坐標的冒泡排序后再根據(5)設計貼合程序，從而提取出相應的貼合信息。

在貼合信息提取完成的基礎上，需進一步分析墻體的打釘面的位置，打釘的位置及打釘的個數，完成整個墻體模型的打釘附屬工藝的初步規劃，從而為裝配序列規劃奠定基礎。

在貼合面的基礎上，與貼合面間隔一個板厚距離的面即為打釘面。當僅存在一個打釘面時，打釘面即為此面。當存在二個打釘面時，根據裝配體的方位選擇打釘面，打釘區域位于整個裝配體左側，那打釘方向往右邊，若在裝配體右側則往左邊打釘，若為上邊則往下打釘，若為下邊則往上打釘。而打釘位置則在貼合面交集區域形心的基礎上，根據貼合面交集區域的面積大小，設置合理的長、寬方向間隔進行網格化打釘。

如圖3所示，設兩面在XOY平面下貼合，兩貼合面的z坐標相同，令z=zsame，

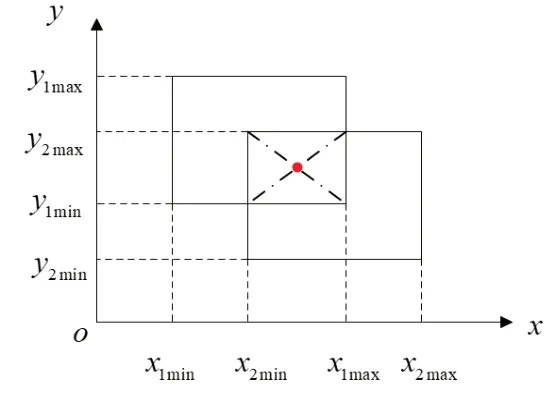
圖3 貼合面交集區域形心圖

ypamx與ypmin的定義類似xpmax與xpmin，則形心坐標(x0，y0，z0)可表示為：

若x方向設定打釘間隔為Δx，y方向為Δy，那么該貼合區域打釘個數N可以表示為：

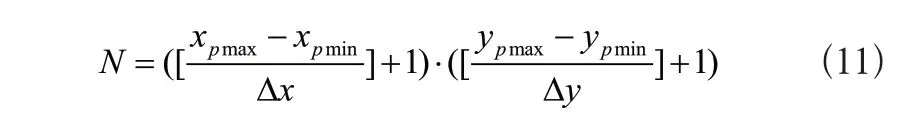
結合Assembly：：AddMate5和Assembly：：AddC -omponent5的API，設計程序可以自動完成墻體打釘分析，生成打完釘后的墻體模型。

2 墻體的裝配序列規劃及評價

針對打完釘后的墻體模型，做適當編碼處理后，便要尋找合理的表達方式充分表達該墻體的模型信息，從而便于生成裝配序列。常用的模型有AND/OR圖，節點圖等表達方式，但便于計算機處理的仍然是矩陣模型。

針對多緊固件裝配體模型，這里給出了緊固件連接矩陣模型和緊固件阻擋矩陣模型來表達模型。設打釘后的墻體有n個木板零件，m個緊固件，行代表緊固件，列代表木板零件，編碼規則是裝配體所有零件號碼為1∶n+m，1∶n代表木板零件，n+1∶n+m代表緊固件，緊固件號=矩陣行號+n；則緊固件連接矩陣FAM中的元素aij：

緊固件阻擋矩陣FAM中的元素bij：

裝配序列規劃(Assembly Sequence Planning)，即在裝配體幾何約束的條件下找出一條或多條滿足幾何可行性和在建立一系列評價準則后經綜合評價并篩選出評價值最好的裝配路線過程。而拆卸法的思想只需考慮單方面的約束，因為已拆卸的零件不會干涉后面零件的拆卸，相比于裝配的雙向約束，拆卸法一定程度上簡化了ASP問題的求解難度[6]。緊固件作為特殊的零件，如果在ASP問題中忽略緊固件而單純的研究零件的裝配序列，這樣會忽略重要的模型信息，導致求解出來的序列解不一定滿足幾何可行性，如果考慮所有的緊固件將會導致理論解為n+m個，將會產生組合爆炸問題導致求解速度很慢[10]，因此需要對緊固件進行特別處理。緊固件跟其連接的零件存在一種內在的隱藏優先關系，在實際工程經驗中，一般先拆卸緊固件，在拆卸緊固件所連接的零件，通過建立緊固件與跟其連接零件的內在綁定關系，將大大縮減ASP問題的規模，節省規劃時間。

在已知FAM和FCM條件下求解ASP問題的步驟如下，定義存放序列的數組xulie初始等于φ：

Step1：根據FAM找出未被阻擋的緊固件qi，qi對應的零件號為Si，將所有的qi存放于數組k1；

Step2：遍歷k1數組的元素，根據qi代表的行號搜索矩陣FCM，在該行存在所有為1的列Aj中，對FCM的Aj列求和，若值等于1，將所有的Aj存入數組k2，按順序取出k2中Aj，Aj對應的零件號為Sj，則分別將Si和Sj加入xulie，若不存在和等于1，則返回k1數組的下一個元素，重復Step2；

Step3：刪除矩陣FCM和FAM中qi和Aj對應的行或者列；

Step4：重復Step1，Step2，Step3，如果FAM的行數等于零，則輸出xulie，否則繼續重復；

Step5：遍歷所有數組k1跟k2元素，輸出所有xulie解，將xulie倒序，即為裝配解。

在生成滿足幾何可行性的序列后，需要建立合理的評價指標對序列群進行綜合評價，選出最節省裝配時間的裝配工藝指導生產實際。

傳統的裝配序列評價指標包括幾何可行性、裝配方向改變次數、裝配工具的改變次數，裝配體穩定性、聚合性等。在墻體生產過程中，影響最重要的因素就是墻體的裝配時間。研究表明：產品裝配所需工時占產品生產制造總工時的40%～60%[5]。由此可見裝配時間的提高對產品的高效率生產有著至關重要的影響。所以對于本墻體，擬采用機器人的運動行程作為評價指標。

機器人的運動行程包括龍門平臺運料行程、機器人打釘行程、機器人輔助定位行程。而機器人的運動行程具體可以表征為距離。常用的距離模型包括歐氏距離、曼哈頓距離、閔可夫斯基距離、馬氏距離等，本文利用歐式距離衡量機器人的運動行程。

對于生成的各個裝配序列，由于墻體各個零件的安裝位置固定，所以每個序列的龍門平臺從開始運料到擺放木板零件到相應位置的運動行程和都是相等的；同理，機器人的輔助定位行程和也是相等的，最關鍵的因素即機器人的打釘行程。該打釘行程優化模型類似于TSP旅行商問題，即一個郵遞員如何找出最短路徑，使得他從郵局出發，給n個城市送完信件以后再返回郵局所走的路徑最短。而本文的距離模型就是4個機器人在若干個打釘位置跟機器人原點之間的TSP問題。

設D(Pi，Pj)為點Pi和Pj的歐式距離，假設有n個打釘位置，P={P1，P2，...，Pn}為一條訪問路徑，Pn+1=P1為初始位置[11]，則每一條序列的打釘行程f(x)可以表征為：

其中i≠j；i，j∈{1，2，3，...nk}。

則本優化的模型可以表征為：

優化目標：minf(x)

優化條件：x∈Ω，其中Ω為所有滿足幾何可行性的序列集合。

3 實例分析

貼合信息為打釘信息奠定了基礎，通過貼合信息進一步能得出打釘的位置，初步反映零件之間的位置關系，不僅表達兩部件是貼合的，還能高亮顯示貼合面，如圖4所示。貼合信息的提取為打釘信息的生成墊底基礎。

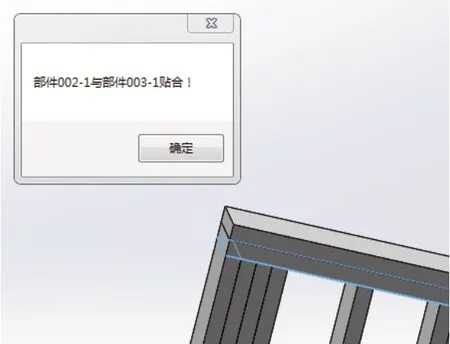
圖4 零件貼合信息提取

貼合信息提取完成后，就要分析墻體的打釘信息。墻體打完釘后的效果如圖5所示，能清晰地反映出打釘的面、打釘的位置及每一個打釘面打釘的個數等信息。

圖5 不同貼合面積打釘情況圖

針對打釘后的模型進行并行簡化、編碼等處理，如圖6所示（括號內數字代表個數），從而方便裝配序列規劃工作。

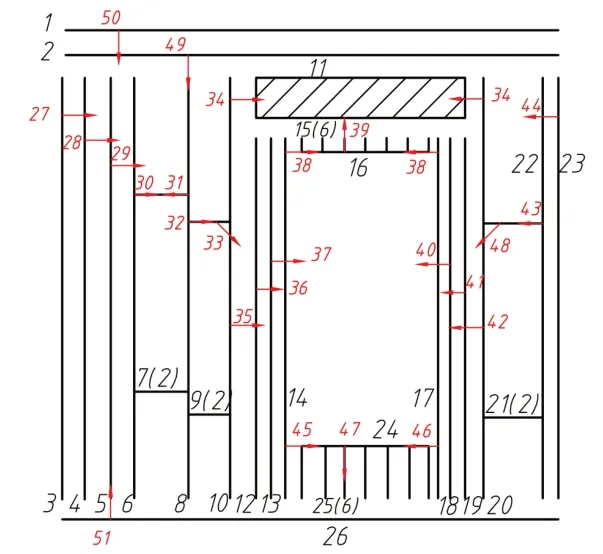
圖6 打釘后模型編碼后圖片

在MATLAB環境下編程，對墻體采用第2節的方法進行裝配序列規劃，取零件24為初始裝配件，通過實驗共得到2412902個可行解，通過評價計算后共得到16組最優序列解，評價函數值為47.1293，綜合裝配資源等因素在16組解中選一組最優解如下：

24 14 45 17 46 25 47 16 38 18 40 19 41 20 42 21 48 22 43 23 44 15 39 13 37 12 36 10 35 9 33 11 34 8 32 7 31 6 30 5 29 4 28 3 27 2 49 1 50 26 51。

針對該最優裝配序列進行演示，演示結果如圖7所示。

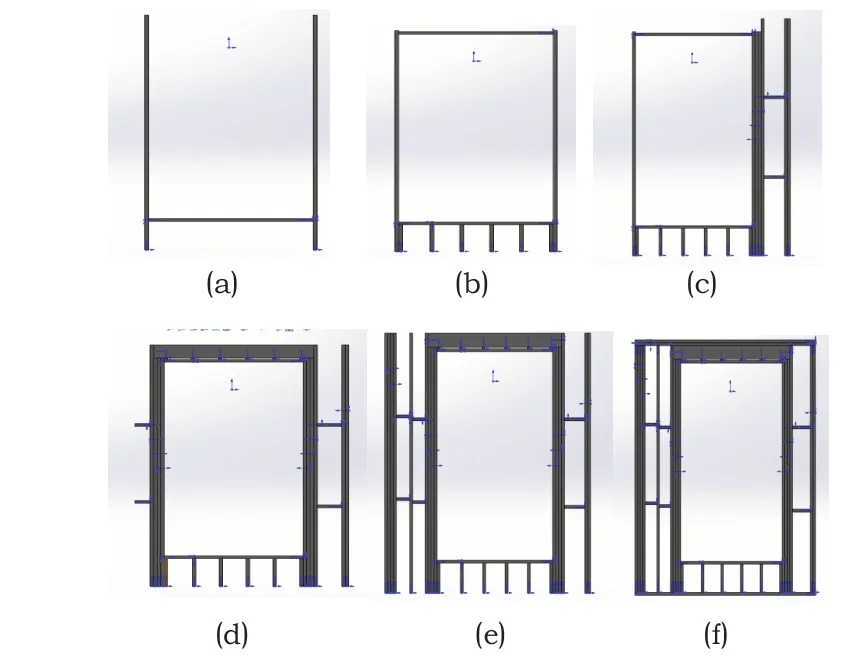
圖7 最優序列的裝配過程

4 結語

本文針對木結構組合墻體的產品報廢率高，自動化程度低的生產現狀，設計了一套包含裝配方案、信息提取、裝配工藝生成、工藝評價等模塊的自動化裝配系統、核心在于利用裝配序列規劃去改進墻體的裝配工藝，產生的裝配序列不僅滿足幾何可行性要求，而且經優化后的序列一定程度上減少了裝配時間，提高了墻體的生產效率。并且從裝配體底層分析、裝配信息提取到裝配序列規劃、評價全由計算機完成，大大提高了木結構組合墻體生產的智能程度，為智能制造行業提供了一個典型范例。