基于變論域模糊PI的三相PWM整流器控制策略設計

姚 強，曾國輝，黃 勃，劉 瑾，韋 鈺

（上海工程技術大學 電子電氣工程學院，上海 201620）

0 引言

三相PWM整流器具有電網側功率因數高、諧波含量少、能量可雙向流動等優點，因而在微電網、超導儲能、電機驅動調速和大功率直流充電樁等領域有著非常廣泛的應用[1，2]。近年來由于能源互聯網概念的提出，傳統電網逐漸進行了一系列的改革升級，使電網更加的智能化，同時也對電力電子控制器的性能提出了更高的要求。但隨著PWM整流器研究的深入，傳統控制策略已經很難在動態和穩態控制性能取得進一步突破，智能控制和新興控制策略研究已成為眾多學者關注的熱點[3]。

由于三相PWM整流器是一個非線性系統，當系統參數發生變化或負載出現擾動時，傳統控制策略因控制參數設置固定，不能夠隨著系統運行狀態的變化而實時改變，因此PWM整流器直流側輸出電壓難以獲得較好的控制效果[4，5]。文獻[6]將滑模變結構引入到PWM整流器電壓外環控制系統中，電流內環采用前饋解耦控制策略，提高了系統的抗干擾能力，但滑模控制自身存在抖振，該文并沒有有效解決這個缺陷。文獻[7]利用三相PWM整流器開關狀態有限的特性，提出了模型預測控制策略，提升了系統的控制精度，但需要對所有開關狀態作用下的預測結果進行在線評估，在線計算量大，對硬件系統要求較高，難以實現實時控制。文獻[8]利用模糊邏輯對PWM整流器的傳統雙閉環PI控制進行改進，模糊控制不需要獲得被控對象的精確數學模型，因此它可以很好地解決非線性問題，并且模糊控制可以實時對三相PWM整流器的PI參數在線調整，但在模糊規則確定的情況下，系統調整的精度不高，自適應能力比較有限。

針對常規模糊PI控制存在的局限性，本文引入一種基于變論域的自適應模糊PI控制方法。該控制策略是將模糊控制與伸縮因子相結合，伸縮因子根據三相PWM整流器輸出電壓誤差大小在線調整論域的范圍，從而使規則的適用范圍得到增加，保證了系統運行時具有較好的動態性能。

1 三相PWM整流器數學模型

三相電壓型PWM整流器的主電路拓撲結構如圖1所示。ea、eb、ec為三相電網電壓；ia、ib、ic為三相交流側電流；L和R分別為交流測濾波電感和等效電阻；C和RL為直流側穩壓電容和負載電阻；iL為負載電流；Udc為直流側輸出電壓。

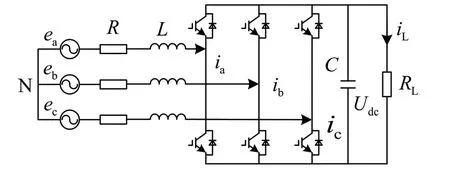
圖1 三相PWM主電路拓撲結構圖

確定整流器等效模型的開關函數如式(1)所示：

根據電壓回路和電流節點方程，在三相電壓對稱的情況下，建立數學模型：

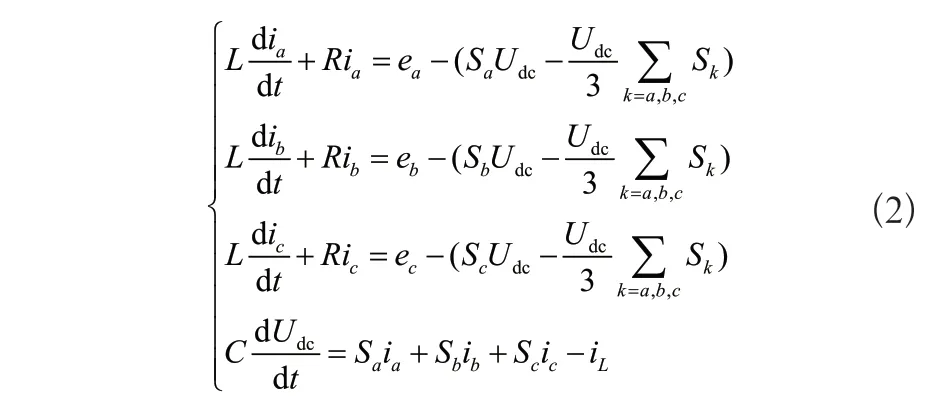
由于交流側電量為正弦變化的交流量，為了使控制策略設計方便，將正弦交流變量轉換成直流變量。因此對式(2)進行坐標變換，建立同步旋轉dq坐標系下的數學模型：

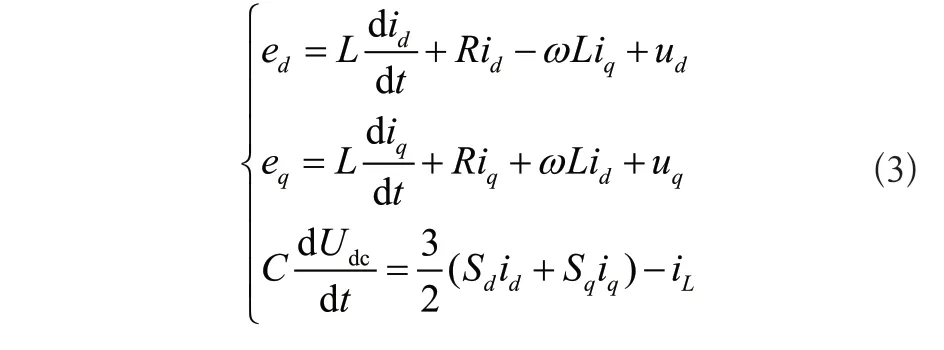
式(3)中，ω為角頻率；ed、eq和id、id分別為網側電壓和電流的d、q軸分量；Sd、Sq分別為開關函數的d、q軸分量。

2 三相PWM整流器控制策略設計

2.1 控制系統結構

本文以傳統雙閉環PI控制策略為基礎，對三相PWM整流器電壓外環控制方式進行改進，將電壓外環的傳統PI控制器替換為參數可實時在線調整的變論域模糊PI控制器，通過伸縮因子對初始論域的自整定，實現外環控制參數的自適應與自調整。電壓外環通過變論域模糊PI控制為電流內環提供有功參考電流i*q，為實現輸入側單位功率因數，通常設參考電流無功成分i*q=0，電流內環將dq坐標系下的采樣電流與參考電流通過內環算法產生SVPWM調制算法所需的輸入電壓參考值。對式(3)進行前饋解耦[10]，控制結構如圖2所示。

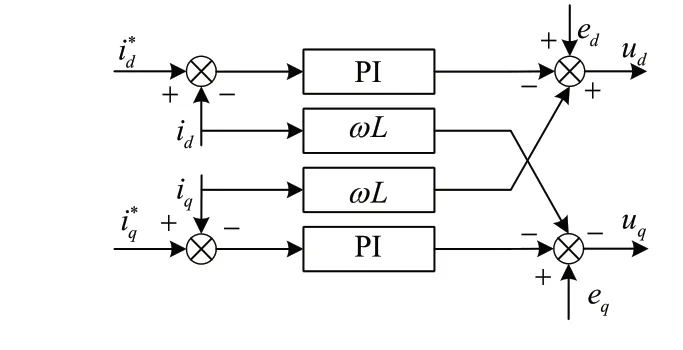
圖2 前饋解耦控制策略結構

控制方程如式(4)所示：

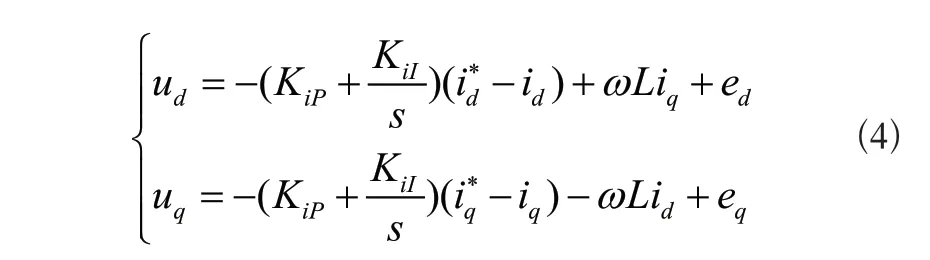
式(4)中，KiP，LiI分別為電流內環比例、積分參數。將式(4)代入式(3)，整理可得下式：

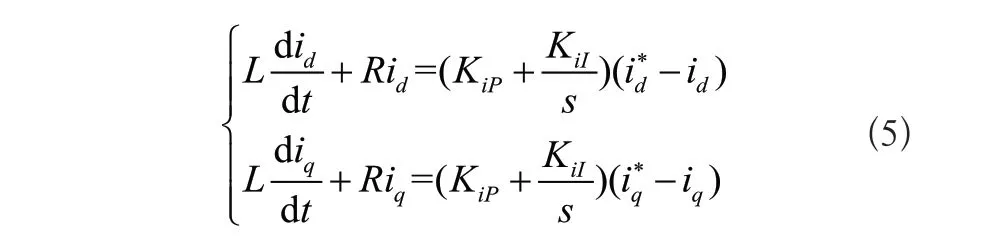
三相PWM整流器電流內環實現了前饋解耦控制，電壓外環采用變論域模糊PI控制，整體結構框圖如圖3所示。

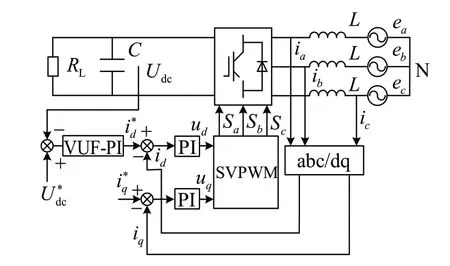
圖3 控制系統結構框圖

2.2 變論域模糊PI控制結構

模糊PI控制雖然在一定程度上了解決了傳統PI控制參數不能實時變化的問題，但由于模糊規則有限，論域范圍不能改變，因此利用伸縮因子實時改變論域范圍，其控制結構如圖4所示。

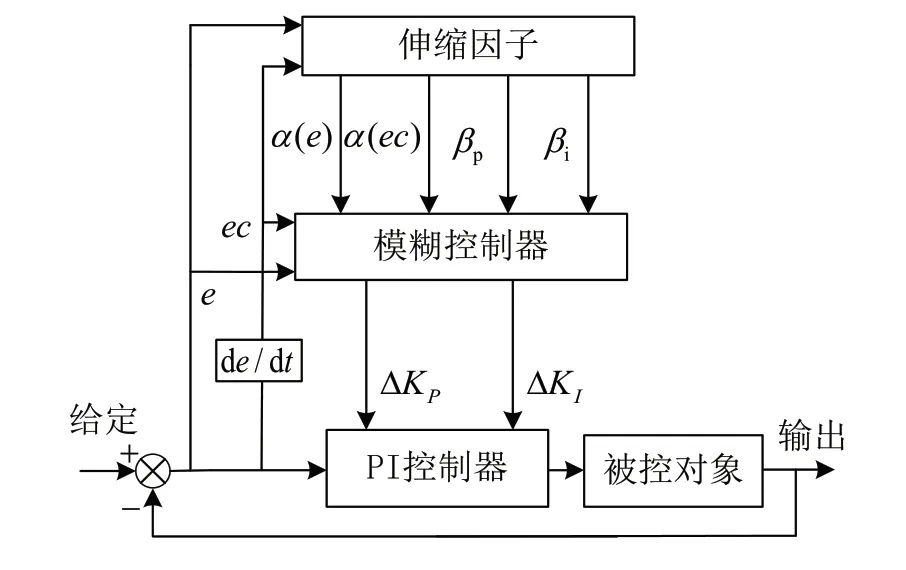
圖4 變論域模糊PI控制結構

圖4中，α(e)、α(ec)分別為輸入變量誤差e、誤差變化率ec的論域伸縮因子，βp、βi分別為輸出變量ΔKP、ΔKI的論域伸縮因子。

2.3 模糊PI控制器設計

本文中設計的模糊PI控制器為雙輸入雙輸出模式，兩個輸入量為直流側輸出電壓實際值與輸出電壓期望值之間的偏差量e以及其偏差變化率ec，兩個輸出量分別為比例系數的修正量ΔKP和積分系數的修正量ΔKI，控制系統對直流側輸出電壓誤差實時檢測，經過模糊控制器處理后得到ΔKP和ΔKI值，從而實現在線實時調整電壓外環PI參數[11]。

輸入輸出變量e、e c、ΔKP、ΔKI的模糊論域均為｛-6，-4，-2，0，2，4，6｝，模糊集合｛NB，NM，NS，ZO，PS，PM，PB｝，對應記作{負大，負中，負小，零，正小，正中，正大}，輸入和輸出狀態變量均采用對稱劃分，隸屬度函數采用三角型隸屬度函數，如圖5所示。

圖5 輸入變量和輸出變量隸屬度函數

根據PI參數調整的經驗及系統分析來構造ΔKP和ΔKI的控制規則，如表1和表2所示。

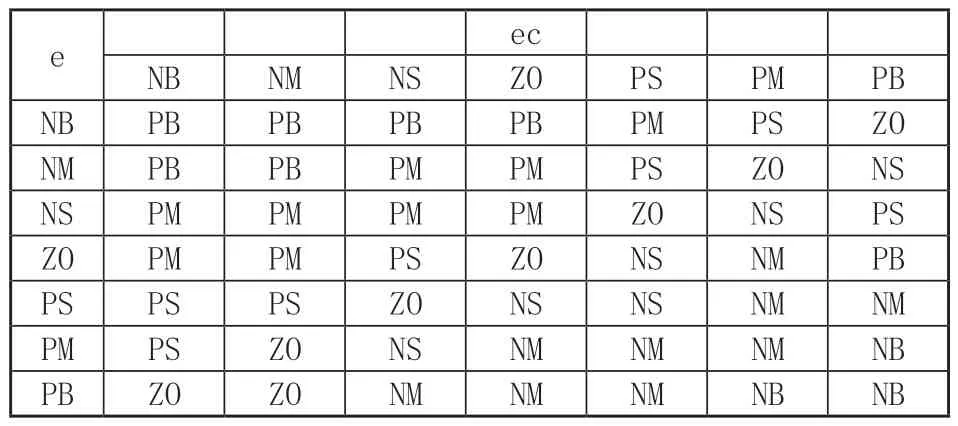
表1 ΔKp模糊規則表

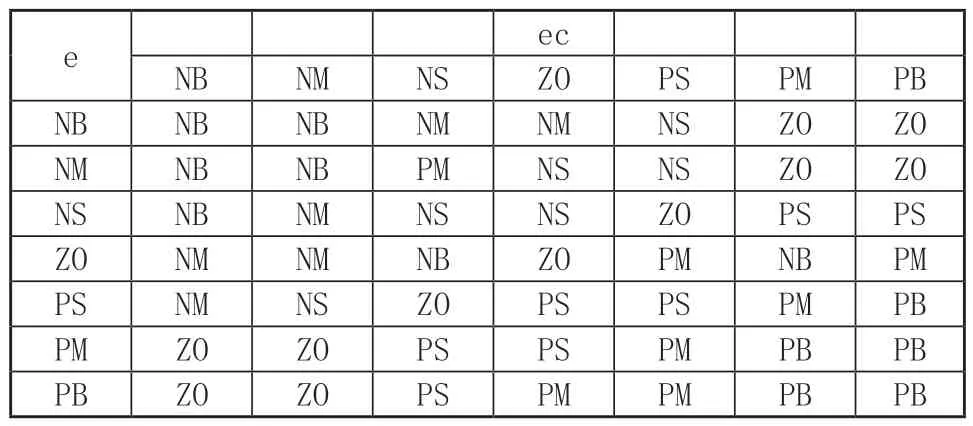
表2 ΔKI模糊規則表

模糊推理采用Mandani最大最小值推理法運算，逆模糊化計算采用重心法[12]。根據以上模糊規則，輸出ΔKP和ΔKI，三相PWM整流器電壓外環PI參數通過模糊控制器完成自調整，其調整式(6)為：

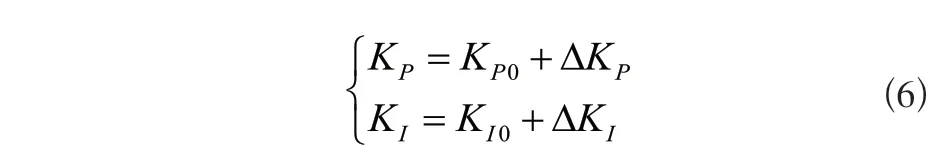
式(6)中，KP0和KI0為三相PWM整流器系統初始PI參數值，Kp和KI為調節后的PI參數。

2.4 論域調整策略

模糊論域范圍大小直接影響三相PWM整流器系統的控制效果，當論域范圍較小時，會導致輸出電壓發生超調，影響系統性能；當論域范圍較大時，控制系統的精度會降低，達不到系統控制要求[13]。為了使系統控制效果得到進一步提升，當系統的運行狀態發生改變時，需要將論域實時調整到適當范圍。

變論域本質思想就是使論域范圍能夠隨著e和ec的變化而實時改變，當整流器輸出電壓誤差較小時，論域應隨之壓縮，減小論域范圍，提高控制精準性；當整流器輸出電壓誤差較大時，論域應隨之擴張，增大論域范圍，提高整流器系統響應速度[14]。論域范圍是通過伸縮因子的改變而進行變化的，因此對于變論域模糊PI控制器的設計核心就在于設計合適的伸縮因子，而伸縮因子對基本論域調節方式如式(7)所示。

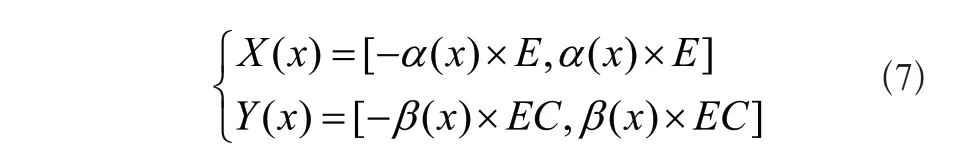
式(7)中，α(x)和[-E，E]分別為輸入變量的伸縮因子和初始論域；β(x)和[-EC，EC]分別為輸出變量的伸縮因子和初始論域，論域的伸縮變化如圖6所示。

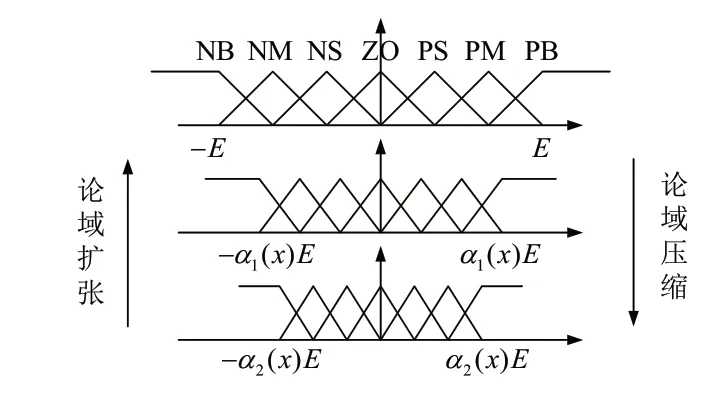
圖6 論域的伸縮變換示意圖

伸縮因子有模糊推理設計和基于函數設計兩種方法[15]。基于函數設計的方法相對簡單，不用設計伸縮因子的模糊規則，簡化了控制系統的設計。輸入輸出伸縮因子常用函數如式(8)所示。

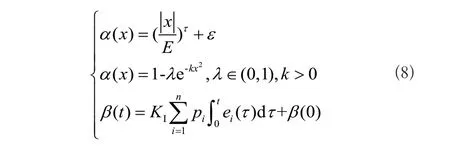
式(8)中，ε為充分小的正數；ei(τ)為輸入變量誤差；pi為輸入變量權重系數；β(0)為輸出論域伸縮因子初值。本文選取輸入輸出伸縮因子如式(9)所示。

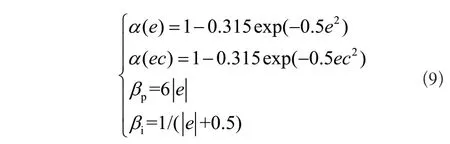
3 仿真驗證

為驗證本文所提控制策略的正確性，在MATLAB/Simulink中對系統進行仿真分析。系統仿真參數如表3所示。

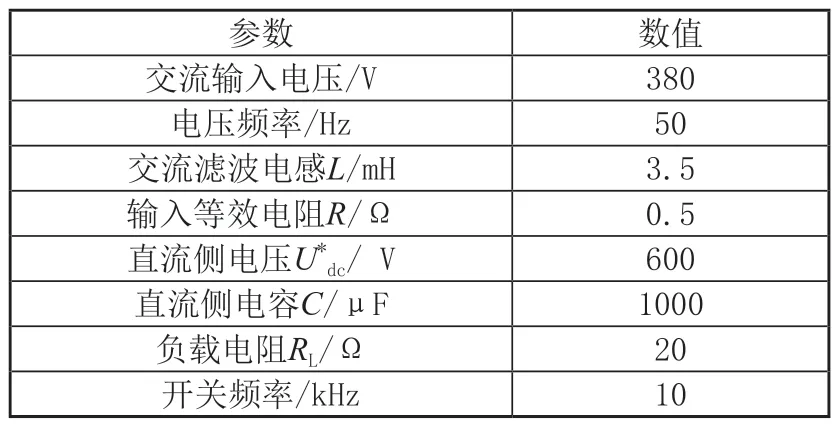
表3 系統仿真參數

三相PWM整流器電壓外環分別采用傳統PI控制、常規模糊PI控制以及變論域模糊PI控制，電流內環均采用前饋解耦控制策略，并且在0.4s時并入一個20Ω電阻，即負載電阻突變為10Ω，其輸出直流電壓仿真波形如圖7所示。

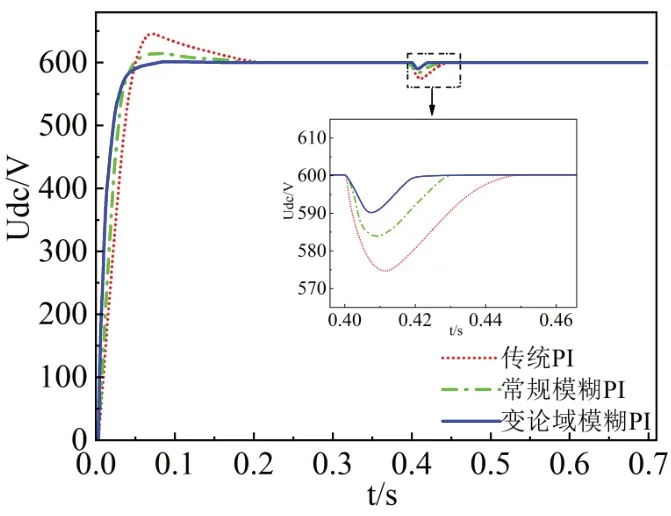
圖7 輸出直流電壓仿真波形

由圖7仿真結果可知，在PWM整流器啟動階段，傳統PI控制和常規模糊PI控制均存在超調量，傳統PI控制超調量為8%，在0.19s達到電壓穩態值；常規模糊PI超調量為3%，在0.18s達到電壓穩態值，而采用變論域模糊PI控制沒有超調量，輸出電壓能在0.12s達到穩態。為了驗證三相PWM整流器的抗干擾能力，在0.4s時負載突變，三種控制方式下的整流器輸出電壓均發生了波動，傳統PI控制方式的直流側電壓最低為574V，經過0.05s重新穩定在600V；常規模糊PI控制的直流側電壓最低為583V，經過0.03s恢復到電壓期望值；變論域模糊PI控制的直流側電壓最低為590V，經過0.02s恢復到電壓期望值。

變論域模糊PI控制相比其它兩種控制方式，系統無超調，具有較快的響應速度；受到負載擾動時，調節時間最短，直流側電壓波動最小，具有較強的抗負載擾動能力，動態性能得到了有效地提高。

4 結語

本文對三相電壓型PWM整流器數學模型進行了分析，針對傳統控制方式的不足，提出一種變論域模糊PI控制策略，將其應用在三相PWM整流器的電壓外環上。通過仿真驗證，與傳統PI控制、常規模糊PI控制方法相比，所提的變論域模糊PI控制策略在動態響應以及抗干擾能力上都具有更好的控制效果，有效地抑制系統超調，減小負載擾動時直流輸出電壓的波動，改善了系統性能。