SCR脫硝系統的強化學習復合串級控制

陳皓煒， 賈新春， 孫小明， 侯鵬飛

(山西大學 自動化與軟件學院，太原 030013)

火電機組運行過程中會產生NOx、粉塵等污染物，對環境造成不同程度的危害。隨著我國相關政策的發布以及對大氣污染物排放要求的日趨嚴格[1]，對火電機組進行超低排放改造已經刻不容緩。目前，由于成本低、效率高、運行可靠等優點，選擇性催化還原(SCR)技術在工業現場應用廣泛，已經成為一項成熟的技術。近年來，雖然在脫硝系統噴氨量控制方面已有大量的研究，但其仍有很大的改進空間。趙海濤等[2]采用神經網絡優化比例積分微分(PID)參數來控制SCR脫硝系統，與傳統PID相比抗干擾性能更好，適應能力更強。白建云等[3]將多模型切換串級控制器用于脫硝系統的控制中，實驗表明該方法的魯棒性好，更加適合變工況的工業過程控制。邢波濤等[4]將神經網絡與動態矩陣控制算法相結合對SCR噴氨量進行控制，結果顯示該算法有更小的波動和更好的控制性能。李健等[5]對線性自抗擾控制進行改進并結合了擴張狀態觀測器，在脫硝系統仿真中取得了滿意的控制效果。

近年來機器學習受到了越來越多學者的關注，其中強化學習策略已成為控制領域的熱點，已廣泛應用于機器人控制[6]、游戲控制[7]、自動駕駛控制[8]等領域。強化學習可以與周圍環境進行互動反饋并對環境產生影響，因此也可以應用到工業過程控制中[9]。在SCR脫硝系統控制方面強化學習的應用較少，PID的應用較多，然而傳統的PID控制在應對脫硝環境多擾動、大慣性等特性時無法取得滿意的控制效果。

針對上述問題，筆者提出一種改進的雙延遲深度確定性策略梯度(ITD3)-比例積分(PI)復合串級控制方法并將其用于SCR脫硝系統控制中。首先，借鑒PID控制思想提出了一種ITD3算法，通過對出口NOx質量濃度設定值與測量值之間的誤差進行微分和積分運算生成新的環境狀態，并將新的狀態與測量值、誤差同時儲存在經驗池中；然后，利用擾動觀測器(DOB)來估計脫硝過程的擾動，并進行前饋補償；最后，對所提出的方法進行仿真對比實驗。該方法為強化學習在脫硝系統噴氨量控制中的應用提供了借鑒。

1 SCR脫硝系統復合串級控制

1.1 SCR脫硝技術

SCR煙氣脫硝是火電機組中最常見的一種脫硝工藝方法。脫硝反應所需溫度一般在300～600 ℃，液氨儲罐中的液氨經過氨蒸發器形成氨氣儲存于氨緩存器中，氨緩存器中的氨氣與空氣混合后經噴氨格柵進入煙道，氨氣和NOx在催化劑(一般為V2O5/TiO2)的作用下轉化為氮氣和水。圖1為SCR脫硝系統在正常情況下的工藝流程。

圖1 SCR脫硝系統

噴氨量過低，SCR脫硝系統出口NOx質量濃度會增加，不僅無法滿足排放最低標準指標，還會污染環境。噴氨量過高可以減少出口NOx質量濃度，但會造成氨逃逸，堵塞SCR下游設備。噴氨量一般由噴氨閥門控制，噴氨量控制過程的平穩對噴氨閥門的壽命有很大影響，因此噴氨量以及噴氨閥門的控制是SCR脫硝系統中至關重要的環節。

1.2 復合串級控制系統

在SCR脫硝系統中，如果只采用簡單的直接控制會使氨氣閥門長期震蕩，影響閥門壽命，因此火電機組現場常常采用串級控制。強化學習復合串級控制系統如圖2所示，Gv(s)為閥門開度到噴氨量的內回路模型；Gp(s)為噴氨量到出口NOx質量濃度的外回路實際模型；din(s)為作用于噴氨量的內部擾動；dout(s)為作用于出口NOx的外部擾動；Gd(s)為外部擾動通道；r為出口NOx質量濃度設定值；y為出口NOx質量濃度測量值;u(s)為噴氨量；c(s)為DOB修正前的噴氨量。在脫硝過程中，噴氨量到出口NOx質量濃度這一階段會受到大量擾動，為了更好地抑制此過程的干擾，引入DOB估計擾動并進行前饋補償。DOB位于圖中虛線框內，其中gn(s)為外回路名義模型Gn(s)的最小相位部分，e-θns為外回路名義模型的純滯后部分，其中θn表示滯后時間；Q(s)為低通濾波器[10]。從圖2可以看出，系統的總擾動為：

圖2 SCR脫硝系統復合串級控制

Dtol(s)=Din(s)+Dout(s)+Dm(s)=

Gn(s)din(s)+Gd(s)dout(s)+[Gp(s)-

gn(s)e-θns][u(s)+din(s)]

(1)

式中：Dtol(s)為系統總擾動；Din(s)為內部擾動；Dout(s)為外部擾動；Dm(s)為模型不匹配造成的擾動。

因此系統輸出為：

y=gn(s)e-θnsu(s)+Dtol(s)

(2)

(3)

(4)

假設系統穩定時總干擾的時域原函數dtol(t)有界，根據定義可知：

Dtol(s)-Q(s)e-θnsDtol(s)=

[1-Q(s)e-θns]Dtol(s)

(5)

根據終值定理可得：

(6)

當選擇Q(s)為低通濾波器時，由于其穩態增益為1，因此有e(∞)=0，說明DOB可以有效地抵消干擾[10]。

2 強化學習基礎

2.1 強化學習原理

在機器學習的分類中，強化學習與監督學習和非監督學習之間有著明顯的差異，其完全不需要事先準備任何數據，而是通過智能體與環境之間進行交互產生動作、狀態以及對動作的獎勵，通過收集這些與控制相關的數據學習得到最優的控制策略，并不斷對模型參數進行更新[11]。

幾乎所有的強化學習算法都是基于馬爾可夫決策過程構建的[12]，一般情況下可以用一個五元組(S,A,R,p,γ)來描述，五元組分別為環境狀態的集合、策略產生動作的集合、執行動作后獎勵的集合、狀態的轉移概率和折扣系數[13]。智能體(agent)通過計算累積獎勵期望的最大值來獲得最佳的控制策略μ*。策略μ產生動作后在狀態s下的獎勵期望如下：

Qμ(s,a)=Eμ[Rt|s,a]

(7)

式中：Qμ為動作價值函數；s為當前狀態；a為狀態s下采取的動作；Rt為累計獎勵。

將式(7)轉化為Bellman公式來計算未來的累計獎勵期望，具體公式如下：

Qμ(s,a)=Eμ[Rt+γQμ(s′,a′)|s,a]

(8)

式中：s′為下一時刻的狀態；a′為下一時刻的動作。

當采用無模型強化學習算法時，不需要計算狀態轉移概率，而是通過迭代Bellman公式獲得近似的最優策略[11]。

(9)

以上函數求解方法雖然簡單，但無法控制復雜的連續系統，因此需要采用神經網絡擬合復雜的函數，并采用梯度下降的方法求解以獲得最優策略。

2.2 深度確定性策略梯度算法描述

谷歌團隊借鑒深度Q學習算法提出了可以用于連續動作控制的深度確定性策略梯度(DDPG)算法，因此筆者以DDPG算法為基礎對SCR脫硝系統的控制進行研究。

DDPG算法在與SCR脫硝系統進行交互后會產生動作、狀態和獎勵值，將這些經驗數據儲存于經驗池中，當DDPG算法進行策略學習時，隨機從經驗池采樣數量為M的(st,at,rt,st+1)樣本,其中st、at和rt表示t時刻的環境狀態、策略產生的動作以及獎勵，st+1表示t+1時刻新的環境狀態。DDPG算法的深度學習部分由Actor網絡和Critic網絡組成，該算法將策略梯度和隨機梯度相結合，因此Actor網絡和Critic網絡均由2套神經網絡——target網絡和online網絡組成。target網絡采用軟更新，online網絡采用梯度更新。這種雙網絡機制減少了數據的相關性，有利于網絡的進一步收斂。Actor網絡和Critic網絡分別用來產生動作決策以及對動作決策進行評價，對動作決策的評價指導著動作決策的更新方向。各網絡的更新方式如下。

Q(s,a|θQ)為Critic online網絡的輸出Q值。Actor online網絡對策略參數θμ進行更新，并根據輸入的矩陣狀態s選擇使輸出Q值最大化的動作輸出a，a=μ(s|θμ)+N，其中N為隨機噪聲。在與環境交互后會產生下一時刻的狀態和獎勵。Actor網絡的更新公式[14]如下：

?θμJ(θμ)≈

(10)

式中：?θμJ(θμ)為性能指標對Actor online網絡參數θμ的梯度；?aQ(s,a|θQ)為輸出Q值對動作a的梯度；μ(s|θμ)為Actor online網絡學習到的策略；?θμ(s|θμ)為μ(s|θμ)對參數θμ的梯度；上標μ表示Actor online網絡。

Critic online網絡根據輸入的狀態s和動作a計算輸出Q值，具體更新公式[15]如下：

(11)

yt=r(st,at)+γQ′[st+1,μ′(st+1|θμ′)|θQ′]

(12)

式中：L為Critic online網絡的損失函數，通過最小化L來更新網絡參數；yt-Q(st,at|θQ)為時序差分(TD)誤差，其中yt為TD目標值；上標Q′表示Critic target網絡,μ′表示Actor target網絡。

target網絡根據online網絡的賦值對參數進行軟更新。公式如下：

θQ′←τθQ+(1-τ)θQ′

(13)

θμ′←τθμ+(1-τ)θμ′

(14)

其中，τ為軟更新系數，τ越小，網絡更新的幅度越慢，算法越穩定，但學習速率也越慢。

3 強化學習控制器設計

3.1 TD3算法

DDPG算法雖然在連續任務中有優勢，但其在獲得錯誤動作后很容易朝著錯誤的方向進行，在有限時間內會造成低效率學習，DDPG算法還存在Q值過高、探索能力較差和控制不穩定等問題，針對這些缺點，Fujimoto等[16]對DDPG算法進行改進，提出了雙延遲深度確定性策略梯度(TD3)算法。TD3算法相比DDPG算法主要改進了以下3點：

(1) 雙Critic網絡[17]。在DDPG算法的基礎上增加了一套完全獨立的Critic網絡，使用min函數比較2套Critic target網絡的Q′，選取最小Q′值并將此值作為更新目標進行更新，用來解決Q值估計過高的問題。改進后的公式如下：

(15)

(2) Actor網絡延遲更新[18]。Critic網絡估計誤差較大時，Actor會朝著錯誤的方向產生新動作，錯誤次數的增加會大大降低訓練效率，嚴重時會產生局部最優，因此Actor網絡需要在Critic網絡進行多次更新后再進行更新，降低Critic錯誤更新造成的危害，提高Actor網絡的收斂速度。

(3) 目標策略平滑[19]。在Actor target網絡中添加隨機噪聲，防止Q值出現過擬合，增加算法穩定性。具體公式如下：

(16)

3.2 ITD3算法

SCR脫硝控制系統已知的環境狀態有出口NOx質量濃度測量值以及設定值與測量值之間的誤差，TD3算法單單依靠這2個環境狀態變量很難獲得較好的控制策略。PID是實際工業過程控制中使用最普遍的控制器，因此借鑒PID控制思想提出了一種ITD3算法，算法原理如圖3所示。ITD3算法在收集狀態信息后計算出口NOx質量濃度設定值與測量值之間誤差的微分和積分，將誤差的微分和積分作為SCR脫硝系統新生成的環境狀態，與出口NOx質量濃度測量值、誤差同時儲存于經驗池中，大大增加了策略學習的數據量。通過與PID控制思想的結合，使ITD3算法可以更好地應用于工業過程控制。

圖3 ITD3算法原理圖

3.3 獎勵機制設計

強化學習的獎勵機制是實現有效控制的關鍵，離散的獎勵機制有助于控制系統快速遠離較差的策略，但離散獎勵過多會增加算法的復雜性。而連續的獎勵機制可以加快算法收斂，使控制過程更加流暢平滑[20]，因此將離散獎勵機制與連續獎勵機制相結合，具體獎勵公式如下：

(17)

式中：e為出口NOx質量濃度設定值與測量值之間的誤差;λ為為了防止獎勵值過高而造成策略過度更新的系數，取0.1。

3.4 Actor網絡和Critic網絡設計

在ITD3算法中，Actor網絡和Critic網絡均使用全連接神經網絡來表示，神經網絡的結構圖見圖4。Actor online網絡和Actor target網絡輸入為收集到的環境狀態，輸出為作用于環境的動作。Actor網絡共有2個隱含層，神經元個數分別為50和20，2個隱含層激活函數分別為softplus和tanh，softplus相當于relu平滑后的函數，其導數一直存在，可以有效防止relu函數出現神經元死亡的問題。Critic online網絡和Critic target網絡輸入為環境的狀態和決策產生的動作，狀態路徑有3個隱含層。第一個隱含層包括100個神經元，選取softplus作為激活函數，第二個隱含層包括50個神經元，選取relu作為激活函數，第三個隱含層包括25個神經元。動作路徑有2個隱含層，神經元個數分別為50 和25，第一個隱含層的激活函數選用softplus。之后將狀態路徑和動作路徑的最后一層通過add層進行合并，add層的激活函數采用relu，最后輸出Q值。

圖4 神經網絡結構圖

4 仿真結果與分析

4.1 實驗準備

將線下訓練好的ITD3控制器作為主控制器對外回路進行實時控制。為了防止閥門調節過大采用PI控制器控制內回路。PI控制器的參數設置為：比例系數Kp=4.25，積分時間常數Ti=2.24。內回路選取540 MW下閥門開度到噴氨量的傳遞函數：

(18)

外回路選取540 MW下噴氨量到出口NOx質量濃度的傳遞函數[21]：

(19)

根據SCR脫硝系統的模型階次選取合適的低通濾波器：

(20)

ITD3控制器在線下訓練時每次迭代隨機生成出口NOx質量濃度的設定值和初始值，通過在隨機空間內進行不同控制目標的試錯來完成與環境的交互以及策略的學習，隨機生成的設定值和初始值的范圍均為(20，60)mg/m3。ITD3算法與TD3算法參數設置相同，具體如下：最大迭代次數為1 200，折扣系數γ=0.99，采樣時間Ts=1 s，仿真時間Tf=150 s，Critic學習率為10-3，Actor學習率為10-4，梯度下降使用的優化器為adam，加載預訓練模型=true;神經網絡L2正則化系數均為10-4;誤差積分的下邊界設置為0，其余狀態邊界均設置為∞;批次樣本數量為128，軟更新系數τ=10-3，經驗池大小為106次，策略延遲更新頻率為4，策略噪聲方差為1.2，策略噪聲方差衰減率為10-5，動作噪聲方差為0.8，動作噪聲方差衰減率為10-5。

4.2 工況對比

為驗證控制性能，對ITD3-PI復合串級控制與TD3-PI復合串級控制、復合串級PID控制和串級PID控制進行對比實驗，其中復合串級PID控制除主控制器與ITD3-PI復合串級控制不同外，其余均相同。

工況一，在450 s時將控制器輸入端(圖2)的出口NOx質量濃度設定值從50 mg/m3調整為30 mg/m3，仿真結果見圖5。從圖5可以看出，由于沒有加入任何擾動，復合串級PID控制和串級PID控制性能完全相同。未改進的TD3-PI復合串級控制只能將出口NOx質量濃度測量值以及設定值與測量值之間的誤差這2項數據作為環境狀態進行策略學習，由于策略學習數據不足導致無法對大遲延、大慣性的SCR脫硝系統進行有效控制。ITD3-PI復合串級控制到達設定值50 mg/m3的上升時間和峰值時間最快，調節時間與復合串級PID控制相當，超調量要小于復合串級PID控制，控制動作更加平滑；ITD3-PI控制在設定值改變后的上升時間與其他控制算法相差不大，峰值時間、調節時間和超調量小于其他控制算法，控制動作整體要比其他控制算法更平穩。綜上所述，在設定值改變前后ITD3-PI復合串級控制器均可以達到更加快速穩定的控制效果。

圖5 工況一控制策略對比曲線

工況二，在控制器的設定值輸入端加入連續的噪聲干擾，噪聲服從標準正態分布，頻率為0.1 Hz。仿真結果見圖6，由于TD3-PI復合串級控制效果太差將不再進行對比實驗。由圖6可知，ITD3-PI復合串級控制算法在噪聲存在的情況下基本沒有波動，由于擾動加在控制器之前，復合串級PID控制和串級PID控制性能完全相同，會受設定值輸入信號噪聲的影響而波動，表明ITD3-PI復合串級控制器在應對控制器輸入信號的噪聲干擾時控制性能更好。

圖6 工況二控制策略對比曲線

工況三，450 s時在噴氨到NOx模型輸入端之間加10%階躍擾動，仿真結果如圖7所示。從圖7可以看出，在加入階躍擾動后ITD3-PI復合串級控制算法的調節時間小于其他2種控制算法，超調量小于復合串級PID控制，比串級PID控制小很多，ITD3-PI復合串級控制算法在加入內部擾動后可以快速穩定地恢復到之前位置，抗干擾性能更好。

圖7 工況三控制策略對比曲線

工況四，450 s時在NOx模型輸出端之后加入10%的階躍擾動，取擾動通道模型為：

(21)

仿真結果如圖8所示。從圖8可以看出，在加入階躍擾動后ITD3-PI復合串級控制算法的調節時間小于其他控制算法，超調量略小于其他控制算法，可以快速穩定地恢復到之前位置。表明DOB在擾動抑制方面起到較好的作用，ITD3-PI復合串級控制算法在加入外部擾動后抗干擾性能更好。

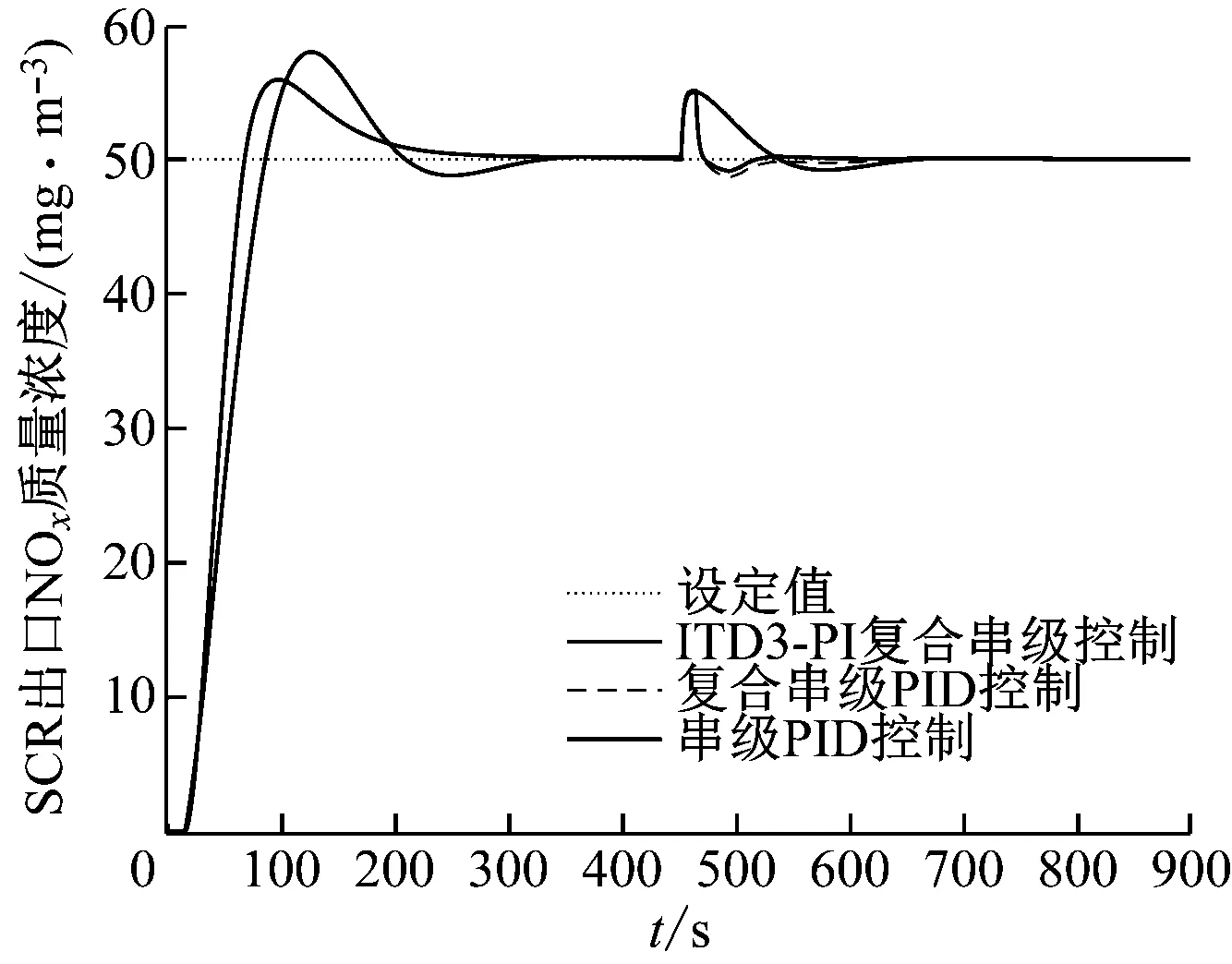
圖8 工況四控制策略對比曲線

為了進一步驗證ITD3-PI復合串級控制算法的控制性能，計算4種工況下各控制算法的絕對誤差積分(IAE)，結果見表1。由表1可知，本文所提方法在4種工況下的IAE值均小于其他控制算法，證明了本文方法具有更好的綜合控制性能。

表1 各工況下的IAE值

5 結 論

針對SCR脫硝系統的特點，提出了一種ITD3-PI復合串級控制算法。首先，借鑒PID控制思想提出了一種ITD3算法，通過對出口NOx質量濃度設定值與測量值之間的誤差進行微分和積分運算生成新的環境狀態，并將新的狀態與測量值、誤差同時儲存于經驗池中，經過改進大大增加了策略學習所需的數據量，使ITD3算法可以更好地用于工業過程控制；然后，利用DOB來估計脫硝過程的擾動，并進行前饋補償；最后，對所提方法進行仿真對比實驗，仿真結果表明本文所提方法控制速度快、超調量小、抗干擾能力強,該控制方案可以為強化學習在SCR脫硝系統中的應用提供新的思路。