淺析如何設計“以生為本”的課堂提問

?甘肅省臨澤縣第一中學 武紅星

1 引言

課堂提問是教師實施下一階段教學計劃的重要參考依據，是教師組織教學的常用手段之一.然而根據教學調研分析發現，教師課堂提問的質量不高，課堂提問往往流于形式.要知道課堂提問并不是簡單的“會不會”“能不能”，這樣的提問過于機械和隨機，難以真正調動學生參與的積極性.課堂提問是一種藝術，只有把握好“度”，控制好“量”，才能用問題點燃課堂的星星之火，讓學生迅速進入狀態，高效完成教學目標[1].那么，什么樣的課堂提問才是有價值的呢？

首先，問題應該是符合學生最近發展區的，可以接受的.問題的設計應帶有一些難度，讓學生“跳一跳”又能夠得著，這樣的問題才能真正激發學生的潛能，提升學習信心，從而引導學生超越現有認知水平，順利過渡到下一個發展區，進而讓學生的學習能力梯度上升.

其次，問題應該是分層的，可促進全體全面發展的.個體差異是不可避免的，為此，教師在問題的設計上也要兼顧學生差異，通過設計分層問題，既讓學困生“夠得著”，又要讓學優生“吃得飽”，從而促進共同進步.

最后，問題應該具有一定的探究性.設計探究性問題，目的是立足于學生，充分調動和發揮學生的潛能，打破傳統“灌輸”教學模式的束縛，為學生提供一個大膽質疑、勇于創新的良好學習氛圍，從而讓學生在探究中不斷突破和發展.同時，在探究中體驗合作的價值，進而培養合作意識.

總之，問題的設計要堅持“以生為本”，為此，教師要足夠了解學生，并依據學生學情合理地創設符合學生“最近發展區”的問題，從而發揮課堂提問的價值.那么，在教學中又應該如何設計問題呢？筆者就如何設計課堂問題淺談了幾點自己的認識，僅供參考！

2 設計激趣性問題

數學的學科特點決定了有些數學教學內容是抽象的、枯燥的，為此，在教學中，若想讓抽象的、枯燥的內容生動起來，不妨引入一些妙趣橫生的教學情境，或者提出一些新穎別致的問題，以此激發學生的好奇心和求知欲，讓學生在問題的驅動下迅速進入學習狀態，誘發學生思維的積極性，促進知識生成.

例如，在講授“數列”前，教師先引入了“米粒”的故事：在古印度有個叫錫塔的大臣，他聰明過人，發明了一種棋子，國王百玩不厭，決定重賞錫塔，于是問：“你想要什么？”聰明的錫塔并沒有要什么金銀珠寶，而是要一些米粒，他說：“我只要第1格放1粒米，第2格放2粒米，第3格放4粒米，第4格放8粒米……只要放滿棋盤上這64個格子就可以.”國王聽后感覺不解，心想：“怎么會有這么傻的人.”你們認為錫塔是真傻嗎？

故事引入后，學生很想知道64個格子里到底可以放多少米粒，自然迅速地進入等比數列的探究中.這樣通過故事情境的引入，為學生創設了輕松愉悅的學習氛圍，有效地化解了數列公式的抽象感，為枯燥的公式探究注入了新的活力，誘發了學生探究的積極性，活化了數學課堂.

3 設計激疑性問題

在數學教學中，當學生思維受阻時，當思考難以深入時，教師可以有意識地創設一些疑問，誘發學生主動探究、深入思考，從而在釋疑的過程中使思維得以深化，學習能力得以加強.另外，學生在學習過程中時常會遇到一些似懂非懂、模棱兩可的問題，若教師能及時捕捉到這些疑點，精準設疑，勢必會在解疑中促進學習能力提升.

例1理解“指數函數”.

師：什么是指數函數？

生(齊)：函數y=ax(a>0，且a≠1)叫作指數函數.

師：很好，現在請大家思考這樣幾個問題：

(1)指數函數中為什么要規定a>0，且a≠1呢？

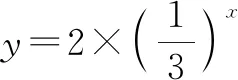
(3)若函數y=(a2-3a+3)ax是指數函數，則實數a的值是什么呢？

指數函數的定義內容很簡單，然而定義中卻隱藏著豐富的內涵，若教學中僅讓學生機械地記住定義，勢必會影響后期的綜合應用，為此，教師通過幾個問題引發了學生對定義的深度思考.學生通過爭論、辨析，不僅深化了對概念的理解，而且教會了學生如何提問，如何思考，有利于培養學生思維的深刻性.

4 設計開放性問題

若要培養學生的獨創能力，就要為學生營造一個開放性的學習環境，讓學生在開放性問題的引導下，從多角度去分析和思考，從而提出自己的新思路和新想法，以此培養學生的創新意識.

例2求證：拋物線y=(a2+1)x2-2ax+1(a為實數)與x軸沒有交點.

本題的證明過程并不復雜，大多學生都可以輕松完成，為了引導學生在此基礎上可以“跳一跳”，發散思維，在本題探究后，教師不妨設計這樣幾個問題：

(1)例2是否可以改編成與二次函數、方程或不等式等相關題目呢？

(2)是否可以對拋物線的方程進行改編，使得在探究與x軸的交點時需要討論a的取值范圍呢？

這樣通過幾個開放性問題引導學生進行創造和改編，幫助學生將方程、函數、不等式等相關知識進行串聯，形成一個縱橫交錯的知識脈絡，便于知識的轉化和遷移.

5 設計探究性問題

在傳統教學的束縛下，為了節省課堂時間，教師在新知授課中大多以“灌輸式”教學模式為主，習題也是為了鞏固新知或應用新知而設計的，公式、定理的記憶靠“死記硬背”，問題求解靠“生搬硬套”，極大程度上限制了學生創新能力的提升.因此，在教學中，必須打破傳統的束縛，給學生一些空間，讓學生經歷一些過程，在探究性問題的引導下培養和發展學生思維的創造性.

例3斜率為1的直線l經過拋物線y2=4x的焦點，且與拋物線相交于A，B兩點，求線段AB的長.

本題的求解并不是很困難，大部分學生將直線l與拋物線y2=4x的方程聯立，求出A，B兩點的坐標，從而求得AB的長；當然，也有部分學生求出A，B兩點的橫坐標，利用定義求解.為了充分發揮本題的價值，教師并不局限于就題論題的講解，通過創設探究性問題來發散思維，提升學生的數學應用能力.

探究1：若不求A，B兩點的坐標，是否能求線段AB的長？

探究2：若將例3改編成：斜率為k的直線經過拋物線y2=2px的焦點F，且與拋物線相交于A，B兩點，是否可求線段AB的長？

通過探究性問題的設計，帶領學生體驗了方程思想的重要應用.另外，探究2中，化特殊為一般，引導學生推理出了過拋物線焦點的弦長公式，讓學生在探究中體驗到了數學學習的快樂，增強了學習信心.

6 設計鋪墊性問題

在新知授課時，教師常設計一些問題讓學生回憶與新知相關聯的舊知，為新知的引出鋪路；在遇到一些較為復雜的、較為抽象的題目時，教師也會設計一些梯度問題幫助學生化繁為簡，為順利求解架橋鋪路；等等.在教學中，借助鋪墊性問題可以引導學生從最熟悉的內容出發，逐層化解，各個擊破，從而提高學生解題的信心，提升解題能力.

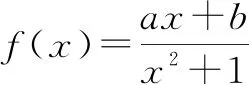
從練習反饋上看，因題設信息量較大，學生感覺無從下手，為了幫助學生掃清思維障礙，教師可以設計幾個鋪墊性的問題，讓學生通過小問題的探究，發現本題的解題思路.

(1)求出f(x)的解析式；

(2)判斷并證明g(x)的單調性；

(3)判斷△ABC的形狀；

(4)判斷△ABC中最大角的余弦值符號；

(5)比較式子2sin2A+sin2C與2sin2B的大小.

通過一層層分解，一層層鋪墊，學生圍繞g(2sin2A+sin2C)與g(2sin2B)的大小關系積極思考，最終順利求解.通過鋪墊性問題的創設啟發學生遇到復雜的問題時不要急于求成，要細心分析，逐漸挖掘出解題的關鍵點，從而圍繞關鍵點逐層剖析，耐心尋找解題的突破口，以此培養學生良好的邏輯分析能力和解題習慣.

總之，教師在教學中應認真籌備，多結合學生實際設計出一些帶有趣味性的、開放性的、能激發學生探究熱情的問題，從而進一步培養學生的思維能力，促進解題能力提升.