NAM降雨徑流模型的參數全局敏感性分析

趙然杭，伍 謀，王興菊，齊 真，周 璐，顧士升

（1.山東大學 土建與水利學院，山東 濟南 250061；2.山東省防汛抗旱物資儲備中心，山東 濟南 250013）

NAM模型由丹麥學者Nielsen和Hansen于1973年首次提出［1］，后經丹麥水力研究所逐步完善，是用于模擬流域范圍內由降雨產生的徑流過程的集總式概念性水文模型［2］。由于NAM模型結構簡單、模型參數較少，因此在我國的流域降雨徑流模擬中得到較為廣泛的應用［3］。NAM模型不僅可以單獨用于流域降雨徑流模擬，也可以與MIKE11水動力模型耦合進行河道洪水過程模擬［4］。

模型概化使得模型與實際的物理過程差異較大，且NAM模型中很多參數難以通過實測方式獲取，需要通過模型率定獲得，導致參數值存在一定的不確定性，從而影響模擬預測結果［5-6］。參數敏感性分析是水文模型構建與應用的關鍵環節，其目的在于定性或定量評估模型參數對模擬結果的影響，確定參數的重要程度，從而識別敏感參數，以提高模型參數率定的效率，降低參數值的不確定性影響［7］，避免出現異參同果現象［8］。參數敏感性分析方法可根據作用范圍分為局部敏感性分析方法和全局敏感性分析方法，局部敏感性分析方法只分析單個參數對模型輸出結果的影響程度，而全局敏感性分析方法檢驗多個參數及參數間相互作用對模型輸出結果產生的影響［9］。常見的全局敏感性分析方法有偏相關法［10］、Sobol法［11］、FAST法［12］等。

近年來，國內外學者對水文模型的敏感性進行了相關研究。劉松等［13］聯合運用Morris和Sobol法對三水源新安江模型進行了全局輸出結果分析，研究了參數間的相關性對模型參數敏感性的影響；溫婭惠等［14］基于單目標與多目標GLUE方法研究了新安江模型參數的不確定性和敏感性，表明多目標函數條件下的模型參數不確定性范圍較大；于永強等［15］基于LH-OAT敏感性分析方法分析了MIKE11模型參數的全局敏感性，表明降雨強度、雨型和評價目標不同會影響模型參數的敏感性；Werkhoven等［16］對SAC-SMA模型參數進行全局敏感性分析，優先考慮敏感參數，降低了模型維數。Liu等［17］通過耦合Morris分析方法與NSDE算法對MIKE／NAM降雨徑流模型進行參數敏感性分析與率定，篩選了模型敏感參數，提高了模型率定的效率；Zaghloul等［18］利用人工神經網絡研究了SWMM模型參數的全局敏感性，并與重復試驗結果進行對比分析。目前對NAM模型的參數敏感性分析較少且主要針對其中部分參數的局部敏感性，如李磊等［19］利用擾動分析法，分析了NAM模型中5個不同參數的局部敏感性；王振亞等［20］基于灰色系統關聯度分析方法研究了NAM模型中地表蓄水層最大含水量、淺層蓄水層最大含水量、地表徑流系數、壤中流系數、匯流時間常數對徑流深、洪峰流量和峰現時間模擬結果的影響；解恒燕等［21］基于擾動分析法分析了NAM模型中9個主要參數的敏感性。以上研究表明，水文模型參數在高維空間通常會表現出較強的相關性［7］，針對NAM模型部分參數的局部敏感性分析，忽略了模型參數之間的相互作用對模擬結果的影響，因此有必要利用全局敏感性分析方法對NAM模型參數進行敏感性分析。

筆者以小清河黃臺橋斷面以上321 km2為研究區域，采取拉丁超立方抽樣方法隨機抽取1 000組初始模型參數，利用互信息法和偏秩相關法對NAM模型參數進行全局敏感性分析，研究NAM模型參數對模擬結果中的洪峰流量、峰現時間、徑流總量的影響，以進一步提高模型模擬精度和減少建模工作量。

1 模型與方法

1.1 NAM模型

NAM模型是一個用于模擬自然流域降雨徑流過程的集總式概念性水文模型［22］。模型中影響流域水循環的土壤狀態被描述為一系列簡化的數學語言形式，并將流域產匯流分為融雪蓄水層、地表蓄水層、淺層蓄水層、地下蓄水層4個相互關聯的蓄水層進行模擬計算，每一層代表流域內不同的物理元素。

NAM模型的參數及輸入量是定義在整個流域上的，即為流域的平均值［23］。模型要求的輸入數據有限，主要包括降雨量數據、蒸發量數據和模型參數。NAM模型的主要參數及其一般取值范圍見表1。

表1 NAM模型主要參數及其取值范圍

1.2 互信息法

互信息是指兩個及兩個以上變量之間共享的信息量［24］，用于度量隨機變量間的相互影響程度，即變量間的相關性大小，互信息越大，相關性越強。互信息法分析得出的R統計量可識別NAM模型參數與輸出的徑流總量、峰現時間、洪峰流量之間的非線性相關關系，用于NAM模型參數的全局敏感性分析。但R統計量只能識別參數敏感性的大小，無法識別NAM模型參數與輸出的徑流總量、峰現時間、洪峰流量之間的正負相關關系［25］。

兩隨機變量X與Y之間的互信息定義為

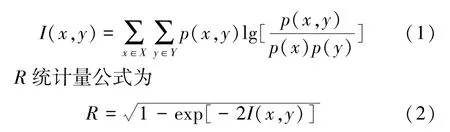
式中：p（x）為離散型隨機變量X取值x的概率；p（y）為離散型隨機變量Y取值y的概率；p（x，y）為X取值x、Y取值y同時發生的概率。

1.3 偏秩相關法

偏秩相關分析是一種非參數統計分析方法，在等級位差的基礎上，通過控制其他因變量對輸出結果的影響來分析兩個變量之間的相關關系［26］，可準確地反映自變量與因變量之間的線性關系，用于分析參數的全局敏感性。其P值（偏秩相關系數）的絕對值大小與計算值正負可分別識別參數敏感性的大小及輸入參數與輸出結果間線性關系的正負。

令輸出結果為Y，輸入參數為X1，X2，…，Xn，設這n＋1個變量之間的Spearman秩相關系數r組成的矩陣為T，求矩陣T的逆矩陣得矩陣C。

第i個輸入參數Xi與輸出結果Y之間的偏秩相關系數PXi為

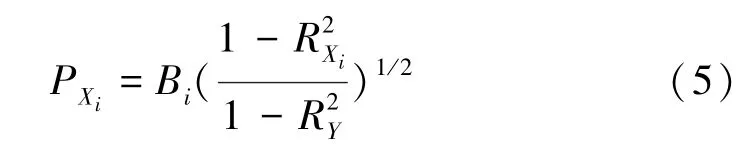
2 研究區域與模型構建

選取小清河黃臺橋斷面以上321 km2為研究區域，該研究區域位于山東省濟南市，包括整個濟南市主城區和南部山區及部分西北郊區，屬溫帶季風氣候區，降水主要集中于6—9月，多年平均降水量為671.1 mm。研究區域內設有黃臺橋、東紅廟、燕子山、劉家莊、吳家鋪、紹而和興隆7個雨量站。

通過對研究區域內7個雨量站2009—2013年的實測降雨資料及流量資料進行分析研究，選用20120708、20130709和20130723場次暴雨洪水過程進行參數率定，并以20110702、20120818和20130719場次暴雨為基準進行驗證。根據率定期內3場暴雨洪水過程得出流域率定參數，見表2，模擬計算結果見表3和圖1。

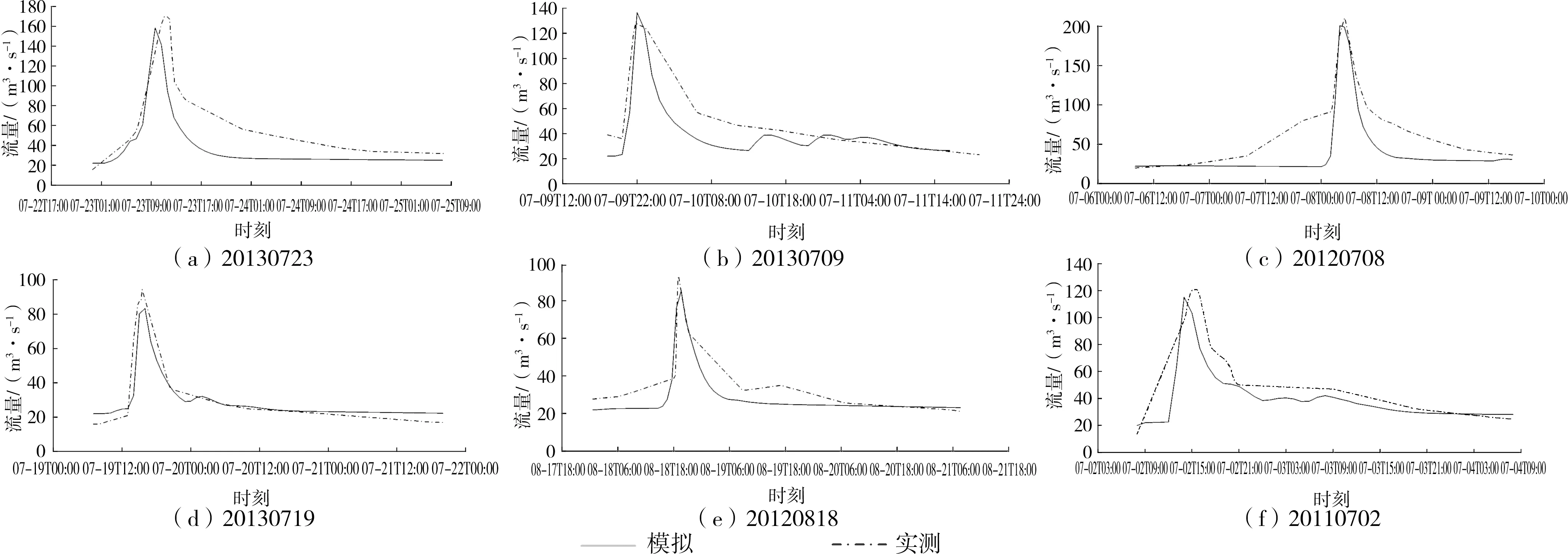
圖1 率定期與驗證期洪水過程模擬結果

表2 NAM模型模擬參數率定結果

表3 各場次降雨洪水模擬結果

在3場率定洪水場次中，確定性系數R2分別為0.938、0.901和0.890，洪峰流量誤差分別為-1.67%、9.77%和-0.18%，峰現時間誤差分別為42、-24、60 min。在3場驗證洪水場次中，確定性系數R2分別為0.915、0.903和0.883，洪峰流量誤差分別為-3.01%、-5.39%、-4.65%，峰現時間誤差分別為60、12、0 min。綜上，本模型對率定期和驗證期共6場次暴雨洪水模擬計算的確定性系數均大于0.85，洪峰流量相對誤差均小于20%，峰現時間誤差均小于180 min，根據《水文情報預報規范》可知，本模型的模擬精度達到良好水平，可以反映該流域流量的變化規律。說明NAM模型在研究區域內有較好的適用性，可用于模型參數的全局敏感性分析。

3 結果與分析

利用拉丁超立方抽樣方法在9個參數值各自取值范圍內隨機抽取1 000組初始模型參數，通過MATLAB編寫腳本寫入NAM模型的輸入文件中，將1 000個輸入文件依次代入模型進行模擬計算得到相應的洪峰流量、峰現時間和徑流總量，再將參數值、模擬結果組成3個10×1 000的矩陣，利用互信息法和偏秩相關法對NAM模型進行全局敏感性分析，敏感次序排第一和第二的參數即為敏感參數。

3.1 互信息分析

互信息分析方法得到的各參數對洪峰流量、峰現時間和徑流總量的敏感性分析結果見表4。

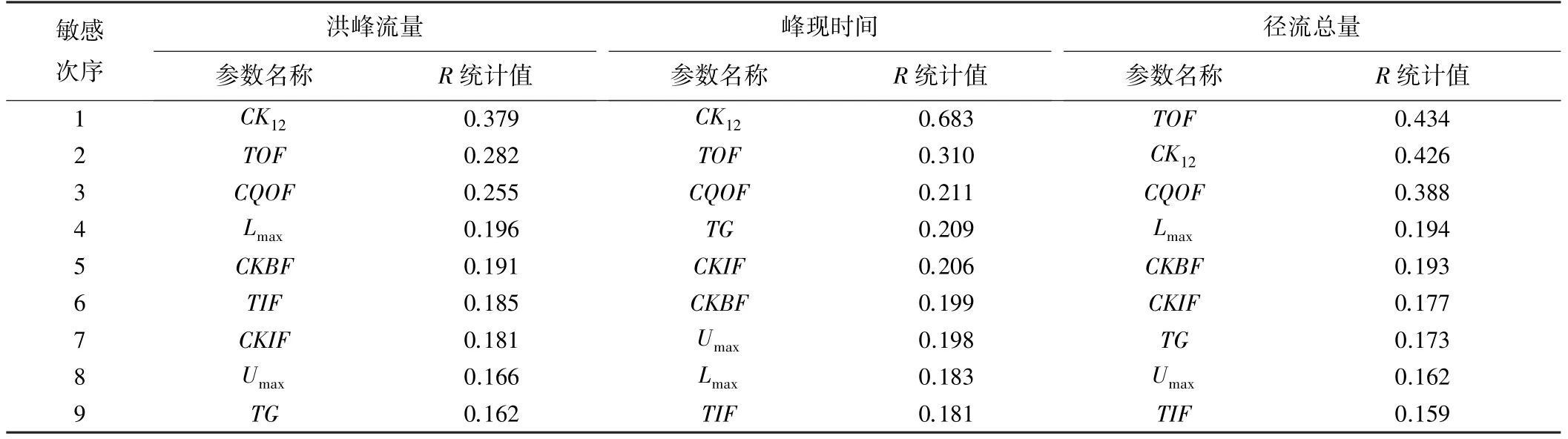
表4 互信息分析結果

根據表4中的R統計值可以判斷參數和輸出結果之間非線性關系的強弱，即參數敏感性的大小。

對于洪峰流量，9個參數的R統計值處于0.162～0.379之間，說明各參數與洪峰流量的非線性關系較弱。其中，參數CK12的R統計值最大，為0.379，說明與其他參數相比，CK12的參數敏感性較強。對于峰現時間，C K12的R統計值最大，為0.683，說明CK12為最敏感參數，與峰現時間的非線性關系強于其他參數；第二敏感參數是TOF，R統計值為0.310。對于徑流總量，敏感參數分別為TOF和CK12，R統計值分別為0.434和0.426。

3.2 偏秩相關分析

偏秩相關法得到的洪峰流量、峰現時間和徑流總量對各參數的敏感性分析結果見表5。

表5 偏秩相關分析結果

由表5中P值的絕對值大小可以得出參數和輸出結果之間線性相關關系的強弱，即參數的敏感性大小。P值正負可以反映參數和輸出結果之間線性相關關系是呈正相關還是負相關。

對于洪峰流量，最敏感的參數是TOF，P值為-0.598；第二敏感參數是CK12，P值為-0.418，說明參數TOF和C K12與洪峰流量的線性相關關系強于其他參數，均為負相關關系。

對于峰現時間，參數CK12的P值最大，為0.817，說明CK12為最敏感參數，與峰現時間的線性相關關系強于其他參數，呈正相關，在率定過程中可優先率定參數C K12。

對于徑流總量，最敏感的參數是TOF，P值為-0.594；第二敏感參數是CK12，P值為-0.434，說明TOF和CK12與徑流總量的線性關系強于其他參數，均為負相關關系。

3.3 結果對比分析

將偏秩相關分析的結果和互信息分析的結果進行對比發現，對于洪峰流量，兩種方法求得的敏感參數都為TOF和CK12。在互信息分析結果中，參數CK12的R統計值為0.379，TOF的R統計值為0.282，說明參數CK12的敏感性強于TOF；在偏秩相關分析結果中，參數CK12的P值為-0.418，TOF的P值為-0.598，說明參數CK12的敏感性弱于TOF。

對于峰現時間，兩種方法求得的最敏感參數都是CK12，互信息法求得的R統計值為0.683，偏秩相關法求得的P值為0.817，說明C K12與峰現時間的線性關系更為顯著。

對于徑流總量，兩種方法求得的最敏感參數都是TOF，互信息法求得的R統計值為0.434，偏秩相關法求得的P值為-0.594，說明TOF與徑流總量的線性關系更為顯著。

3.4 討 論

對于洪峰流量，兩種方法求得的敏感參數均為CK12和TOF，但兩個參數的敏感次序不同，考慮到互信息法和偏秩相關法分別基于非線性和線性來識別敏感性參數，因此參數的敏感次序排列有所不同是不可避免的。對比其他學者對NAM模型參數敏感性分析結果，李磊等［19］的研究結果表明參數CK12對洪峰流量影響較大，與本文的結論一致。

對于峰現時間和徑流總量，互信息法和偏秩相關法求得的最敏感參數結果一致，峰現時間的最敏感參數均為CK12，R值為0.683，P值為0.817，說明與峰現時間的線性關系較為顯著，呈正相關；徑流總量的最敏感參數均為TOF，R值為0.434，P值為-0.594，說明與徑流總量的線性關系較為顯著，呈負相關。兩種方法的共同使用，避免了只使用單一方法的局限性，可全面地識別敏感參數。

對比其他學者對NAM模型參數敏感性分析結果，王振亞等［20］的研究表明參數CK12與峰現時間的關聯度最大，C QOF次之，本文中CQOF的敏感次序為3，其原因為前者未考慮參數TOF對峰現時間的影響；解恒燕等［21］的研究表明參數Lmax和Umax對徑流總量的影響較為明顯，但其研究區域Fisher小流域地勢較為平坦且多為自然地貌，而本文研究區域小清河黃臺橋斷面以上321 km2流域，地勢南高北低且多為城市地形，說明在不同下墊面情況的流域，對徑流總量影響最大的參數不同。

4 結 論

針對NAM模型參數，利用拉丁超立方抽樣方法抽取模型輸入樣本，使用互信息法和偏秩相關法進行NAM模型參數全局敏感性分析，得到以下結論。

（1）通過拉丁超立方抽樣方法抽取了1 000組模型輸入樣本，保證了NAM模型參數值數據的代表性和均勻性。互信息法通過分析參數與模擬結果間的非線性關系識別敏感參數，偏秩相關法通過分析參數與模擬結果間的線性關系識別敏感參數，且兩者均為全局敏感性分析方法，兩種方法共同使用可避免只使用單一方法存在的局限性，全面準確地識別敏感參數，保證結論的合理性及可靠性。

（2）在兩種不同敏感性分析方法結果中，參數TG、TIF、CKIF、Umax和Lmax的R統計值和P值均較小，說明這些參數為不敏感參數，在模型率定時可以根據經驗取固定值以提高率定效率。TOF和CK12是對洪峰流量敏感性最大的參數，且與洪峰流量呈負相關；CK12是對峰現時間敏感性最大的參數，隨著CK12增大，峰現時間會相應延長；TOF是對徑流總量最為敏感的參數，呈負相關，隨著TOF增大，徑流總量會相應減小。

（3）通過全局敏感性分析，識別了NAM模型的敏感參數，為后續模型率定及耦合提供參考和指導，減少建模的工作量，提高模型率定的效率。