新型裝配墻式質量調諧阻尼器抗震性能研究

尹 航， 劉書賢， 路沙沙， 張貴軍， 聶 偉， 李曉峰， 徐 紅

(遼寧工程技術大學 土木工程學院，遼寧 阜新 123000)

調諧質量阻尼器(tuned mass damper，TMD)自20世紀50年代誕生以來，經過半個多世紀的發展，理論體系逐漸成熟，TMD主要由彈簧、質量塊和阻尼器組成，通常調諧到主系統固有頻率工作。近年來全球已有許多成功的結構實施案例，紐約市的花旗集團中心、橫濱的橫濱地標大廈、迪拜的帆船酒店、紐約市的特朗普世界大廈、臺北的臺北 101 和柏林的電視塔都是配備了TMD的建筑[1]。現階段阻尼器類型有液體調諧質量阻尼器(liquid tuned mass damper, LTMD)[2]、渦流阻尼器[3]、擺式調諧質量阻尼器(pendulum tuned mass damper， PTMD)[4-5]，其基本減震原理是當結構遭受外激勵時，TMD產生與主結構相反的慣性力，抵消部分地震作用[6]，減小外激勵對結構的影響，從而實現減震控制效果。魯正等[7]應用液體調諧和顆粒碰撞協同減振的原理對一種組合型質量阻尼器開展振動臺試驗，發現組合型質量阻尼器在全頻帶內均有減震效果且低頻內減震效果更佳。劉金栓[8]針對一種以單純改變質量來實現頻率可調的被動調諧質量阻尼器，通過振動臺模型試驗研究其可行性及振動控制效果，并利用MATLAB軟件對試驗所測得的結果進行分析。袁康等[9]設計了不同阻尼器鋼片厚度(頻率比)，不同質量塊布置(質量比)的填充墻MTMD減震結構，進行了不同地震輸入水平下的振動臺試驗和動力時程分析。表明對于第一振型為主的多層結構，質量塊布置數量對減震效果影響不明顯，可考慮僅在頂層設置TMD質量塊。趙祥等[10]提出了一種新型變阻尼式TMD，并將該阻尼器安裝在兩層單跨的鋼框架模型結構上。通過對比無控狀態、傳統 TMD 控制狀態和變阻尼式 TMD 控制狀態下鋼框架結構的動力響應，分析了變阻尼式 TMD在不同激勵下的減震控制效果。盧俊輝等[11]設計了兩邊均由U型墊片連接的填充墻作為TMD調節質量塊，得出了填充墻TMD結構中TMD連接參數的計算方法。并通過振動臺試驗分析其減振效果，但設計的TMD裝拆不便，參數不能靈活調整，在結構損傷累積中會發生失諧現象。

無論何種類型TMD，其本質是依靠較大質量塊實現調諧，附加質量勢必會大幅增加造價成本，占用有限的空間資源，而如何充分利用現有建筑的各組成部分的質量，實現減震控制目標，同樣是一個具有廣闊研究意義的課題。有關TMD的研究大多數聚焦在TMD的位置、數量、參數優化等方面的理論分析，忽略了對現有建筑的各組成部分的質量利用來改進提高其工作性能，并且針對該研究方向的TMD減震控制振動臺試驗有所欠缺。

本文設計了一種裝配墻式減震TMD，將傳統墻體設置成具有TMD減震特性的墻式TMD，該墻體可充分利用墻體現有質量，節約使用空間，裝配式的構造可實現TMD配件的及時更換。為了檢驗墻體抗震性能，建立了TMD結構耦合運動方程，對無控結構和墻式TMD結構的傳遞函數進行了推導，并通過振動臺試驗對比無控結構和墻式TMD受控結構動力響應，驗證其減震效果。

1 墻式質量調諧阻尼器的設計

在相關研究中所采用的TMD減震結構，需要將特定的調諧質量塊與主結構通過阻尼器連接形成TMD系統，結構構造較為復雜，不便于裝拆，且會增加結構造價。為此，本文自主研發設計了一種新型裝配墻式TMD減震結構。墻式TMD減震結構的主要特點是將傳統建筑結構中不參與結構受力的墻體與主體承重結構分離，二者通過阻尼器與抗壓件連接，如圖1 所示。圖1由彈簧、高強螺栓、螺母、復位拉桿、摩擦橡膠、調壓螺栓、預埋U型鋼片、擋板、質量塊、鐵框、滾輪組組成。整體構造中，擋板與預埋在結構中的鋼片通過螺栓連接，墻體外包鐵框上焊有螺母與墻體共同組成質量塊體系，并與復位拉桿一起由高強螺栓固定，復位拉桿末端套有摩擦橡膠和彈簧。當外激勵發生，墻式TMD在慣性力作用下隨著結構左右平動，彈簧為結構提供恢復力，使結構具有自復位功能，摩擦橡膠與調壓螺栓相連，通過擰動調壓螺栓可調節摩擦橡膠與復位拉桿的正摩擦力，為結構提供所需阻尼，裝拆時只需要擰動高強螺栓便可使復位拉桿與質量塊體系分離，隨意更換結構配件。其中，主結構為主要的豎向和水平受力構件，墻式TMD減震結構不僅具有填充建筑物的功能，同時作為 TMD系統中的質量塊，與消能減振裝置有機結合起來，形成 TMD 系統以耗散地震能量，為了防止激勵發生時TMD質量塊出平面破壞，在隔震支座兩側安置平面限位擋板，具體構造可參考專利[12]。

1.彈簧；2.螺母；3.高強螺栓； 4.復位拉桿；5.摩擦橡膠；6.調壓螺；7.預埋U型鋼片；8.擋板；9.滾輪組；10.質量塊；11.鐵框。圖1 墻式減震TMD示意圖Fig.1 Schematic diagram of wall-mounted shock absorption TMD

2 結構-TMD系統數值模型

袁康等對于填充墻MTMD減震結構試驗表明，對于第一振型為主的多層結構，質量塊布置數量對減震效果影響不明顯，可考慮僅在頂層設置TMD質量塊。基于此，本文墻式TMD減震結構僅于頂層對稱布置，墻式TMD結構的數學模型如圖2所示，根據牛頓力學原理可得到式(1)，各矩陣為

圖2 墻式TMD 的數學模型Fig.2 Mathematical model of wall-tuned mass damper

(1)

矩陣C

矩陣K

式中：X為結構-TMD系統的位移向量，xi為第i層樓板對地面的相對位移(i=1, 2, …,N)，xt為阻尼器對地面的相對位移；xg為由于地震引起的地面位移；m*為加速度質量矩陣;M,C,K均為包含了墻式TMD參數的N+1維矩陣矩陣。其中：M為結構-TMD系統的質量矩陣，mi為第i層樓板的質量(i=1, 2, …,N)，mt為阻尼器的質量；C為結構-TMD系統的阻尼矩陣，ci為第i層樓板的阻尼(i=1, 2, …,N)，采用Rayleigh阻尼假定，即ci=α1mi+α2ki，其中α1，α2為阻尼系數與結構的振動特性有關，ct為阻尼器的阻尼；K為結構-TMD系統的剛度矩陣，ki為第i層樓的剛度(i=1, 2,…,N),kt為阻尼器的剛度。

3 傳遞函數

(2)

式中：HxN(ω) 為第N層結構傳遞函數；Hxt(ω)為墻式TMD傳遞函數，通常以結構頂部傳遞函數為主要控制對象。

為了獲得更準確的墻式TMD參數，使用Den Hartog[13]經典阻尼參數計算式(3)對本文墻式TMD系統進行參數優化，其中αopt為頻率比，ξopt為阻尼比、μ為質量比、ft和fs分別為TMD結構自振頻率和主結構自振頻率。

(3)

根據上述最優參數計算方式，使用MATLAB計算并繪制了不同TMD質量比下的主結構傳遞函數圖，如圖3所示，可以看出墻式減震TMD顯著降低了主結構傳遞函數峰值，隨著TMD結構質量比的增大，調諧頻帶逐漸加寬，傳遞函數峰值逐漸減小，但減小程度逐漸放緩，而安裝減震TMD所需的最優參數(剛度、阻尼)均逐漸增加。Farshidianfar等[14]表明TMD質量比一般為建筑總質量5%～10%，權衡試驗條件，本文質量比取為6%，其傳遞函數峰值減震幅值達60.5%。

具體計算過程如下，將質量比μ=6%，代入Den Hartog式 (3)，計算αopt，ξopt分別為0.943和0.145，將fs，mt回代式(3)進一步計算Kt和Ct，最終可得Kt=17.3 N/mm，Ct=101 N·s/m，運行得到墻式TMD最優參數如表1所示，本文基于此方式對墻式TMD進行參數設計。

表1 結構優化結果Tab.1 Structural optimization results

圖3 傳遞函數對比圖Fig.3 Transfer function comparison chart

4 墻式TMD框架結構振動臺試驗

為了驗證墻式TMD減震效果，對受控體系進行了振動臺測試。研究中使用的振動臺設備由3 m×3 m的平臺組成，額定負載10 t，可雙向水平運動頻率范圍：0～50 Hz，滿載下峰值加速度為1.5g；加速度計采用東華測試生產的IEPE壓電式加速度傳感器。軸向靈敏度(23±5 ℃)107.6 mV/m/s2，量程±5g，最大橫向靈敏度<5%。

試驗對一棟單跨三層框架結構框架模型進行1/10縮尺振動臺試驗，結構尺寸如圖4所示，原型結構層高為3 m，總高為9 m，混凝土強度為C30；柱子尺寸為450 mm×450 mm；框架梁截面尺寸為300 mm×450 mm；框架柱網為6 m×6 m；樓板板厚120 mm；加速度計用字母“A”表示。結構上布置的6處，分別位于臺面中心(A1)、垂直于振動方向每層樓板邊側(A2、A3、A4)、墻式TMD中心(A5、A6)，A6位于結構另一側墻式TMD上，因此，圖4(a)中未畫出，墻式TMD框架結構如圖5所示，基礎使用留有螺孔的10 mm厚鋼板通過M20高強螺栓固定在振動臺臺面。試驗各物理量的相似關系采用量綱分析法確定，以Sl，Sa和SE為基本可控相似常數，為達到響應相似比要求，其余物理量相似關系可由量綱分析推算得出[15-16]，模型采用微粒混凝土與鍍鋅鐵絲構建，根據計算結果，模型結構屬欠人工質量模型，額外增加鉛塊配重[17-18]，最終模型相似比如表2所示。

圖4 框架模型平面尺寸(mm)Fig.4 The plane size of the frame model (mm)

表2 振動臺試驗相似常數Tab.2 Similar constant of shaking table test

圖5 墻式TMD框架結構Fig.5 Wall-tuned mass damper frame structure

5 試驗加載工況

試驗對比分析了，無控框架結構和墻式TMD框架結構的減震效果，每種工況開始前使用0.05g峰值的高斯白噪聲進行掃頻，通過白噪聲掃頻采集模型自振頻率，為了探討輸入地震動特性對試驗結果的影響，選擇三條頻譜成分差異較大、具有代表性的地震波作為臺面輸入地震動，分別是Kobe波、Taft波和Northridge地震波，三條輸入地震波的時程圖及響應譜圖，如圖6所示，依據GB 50011—2010《建筑抗震設計規范》[19]對地震波進行設計，地震波峰值從0.1g逐級增加至0.6g，試驗中對每條地震波的峰值加速度及時間間隔均根據相似關系進行調整。

圖6 地震波時程曲線及反應譜Fig.6 Seismic wave time history curve and response spectrum

6 試驗結果與分析

為獲取結構的動力特性，在試驗開始前通過輸入加速度峰值為0.05g的白噪聲測試，結構模型在無控、墻式TMD受控下結構的自振頻率分別為8.24 Hz，7.84 Hz。由此可知，安裝減震裝置后，結構的自振頻率較無控狀態有所降低，使得結構的周期有一定的延長；減震搖擺墻TMD質量取為6%，墻式TMD參數根據表1得到，單側墻體Kt=8.65 N/mm，Ct=50.5 N·s/m。

6.1 減震工作機理驗證

如引言所述，墻式TMD體系減震原理是TMD質量塊在發生外激勵情況時，產生相反慣性力抵消結構系統的運動，對于這種減震方式的實現，需保證減震子結構的自振頻率與受控主結構相近且運動反向相反，或減震子結構反應延遲不同步。本文通過對減震框架結構(主結構)頂層和墻式減震TMD(子結構)的位移時程曲線進行對比，以驗證減震結構的工作機理。當輸入地震加速度峰值為0.6g時，框架主結構和減震TMD子結構的位移時程曲線，如圖7所示。

從圖7中不難發現，墻式減震TMD在抵抗振動過程中整體呈現平動特性，墻式減震TMD與主結構的動力反應時程曲線形狀相似，但存在一定的相位差，墻式減震TMD位移滯后于主體框架，某些時間節點甚至方向相反，表明結構在振動過程中減震結構與受控結構間發生了相對運動，這種特性體現了模型被動減震的特點。此外，從圖中動力反應時程中可見，墻式減震TMD的位移大于主體結構，其原因在于墻式減震TMD與主體結構非剛性連接，而是由減震彈簧連接，在運動過程中的慣性作用增大了自身動力響應，但由于主子動力響應不同步，使得其慣性力反作用于主體框架上，實現模態傳遞減震功效。

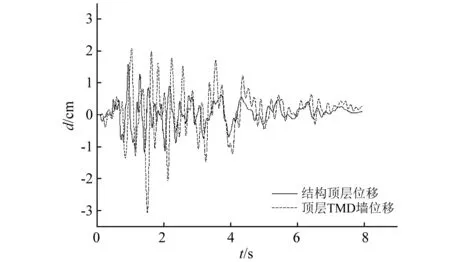
圖7 體框架與減震TMD墻位移時程曲線Fig.7 Displacement time history curve of the main frame and the shock-absorbing TMD wall

6.2 加速度響應分析

為了檢測墻式減震TMD減震性能，對框架模型結構分別進行了Kobe 波、Taft波和North波作用下的振動臺試驗，各工況頂層加速度時程對比如圖8所示。圖8中可以明顯看出，墻式減震TMD在整個地震激勵過程中對結構加速度均產生了振動抑制效果。頂層加速度響應最大值(peak ground acceleration PGA)及減震率在表3給出，結合表3可知，Kobe波作用下的結構響應與Taft波作用下的結構響應相似且均較大，這可能是由于這兩種地震波激勵頻率與主結構自振頻率相近；Kobe波作用下，墻式減震TMD對結構樓層平均減震率為20.32%，Taft波和North波作用下分別為11.7%和12.6%，頂層為減震效果最明顯樓層，最大減震率分別為29.7%，23.6%，26.9%，該結果表明地震波的頻譜成分很大程度上影響墻式減震TMD的減震效果，一般來說越接近結構自振頻率，結構動力響應越大。不同加速度峰值激勵下，各樓層加速度峰值對比如圖9所示，不難看出墻式減震TMD在不同的地震激勵峰值情況下，各樓層均取得了較好的減震效果，頂層減震效果優于其他樓層，且外激勵越大這種減震效果越明顯。

圖8 頂層加速度時程響應Fig.8 Time-history response of top layer acceleration

圖9 樓層加速度峰值對比圖Fig.9 Comparison of peak floor acceleration

6.3 頻譜分析

對從測試中收集到的頂層加速度進行了快速傅里葉變換(fast Fourier transform,FFT)，以了解受控和無控結構之間的動態特性差異，如圖10所示。在三種不同地震激勵下傅里葉變化峰值均出現在結構自振頻率(8.24 Hz)附近，分別為8.99 Hz，8.50 Hz，7.88 Hz，低頻分量的傅立葉頻譜被放大，高頻分量均被衰減。安裝了墻式減震TMD的受控結構，其傅里葉峰值所處頻率均小于無控結構，這可能是由于裝有墻式減震TMD的受控結構的自振頻率較無控結構有所降低，延長了結構振動周期。安裝了墻式減震TMD的受控結構，在三種激勵下均在一定程度上降低了傅里葉峰值，其FFT峰值分別減小了36.9%，36.8%，35.3%，因此，由上述可以推斷，墻式減震TMD具有明顯的減震與頻率調諧作用。

圖10 頂層幅頻響應曲線Fig.10 The amplitude-frequency response curve of the top layer

表3 加速度減震率對比表Tab.3 Comparison table of acceleration damping rate

6.4 位移響應分析

為了更好地分析墻式減震TMD的減震性能，對 Kobe 波、Taft 波和North波作用下受控結構各層的位移最大值進行對比，圖11可看出在三種地震波作用下，結構頂層的位移值均大于結構底層；與加速度響應相似，Kobe 波與Taft波作用下的位移最大值均大于North波作用下的位移最大值，這主要是由于 Kobe 波的與Taft波卓越周期與結構的自振周期較為接近，因而結構的反應較North波作用下結構響應激烈。各工況最大減震率對比如表4所示，結構在加入裝配式墻式減震TMD裝置后，其位移響應顯著降低，且隨著加速度峰值的增加，位移減震效果越發明顯。由于調諧類阻尼器以控制結構的第一振型為主，因此，墻式減震TMD安置于結構的頂層，可以看出其對結構頂層的位移控制效果明顯優于結構底層的控制效果；對比位移與加速度減震效果，整體來說該墻式減震TMD對位移的控制效果好于對加速度控制效果。

值得注意的是，墻式減震TMD在加速度峰值為0.6g的Taft波作用時，加速度和位移減小率分為23.6%和27.8%，為三種地震波中最低，根據Den Hartog的研究表明，外激勵主頻率成分與結構自振頻率越接近減震效果越明顯，而Taft波相較于其余兩種地震激勵其頻率成分更接近結構自振頻率，比較圖11中Taft波引起的結構位移，分析造成此現象的原因可能是由于墻式減震TMD位移過大與主結構預埋鐵皮發生碰撞，導致墻式減震TMD的調頻作用受到影響。在后續的試驗中增大了墻式TMD位移極限，有效增大了墻式減震TMD在各地震激勵下的減震能力。

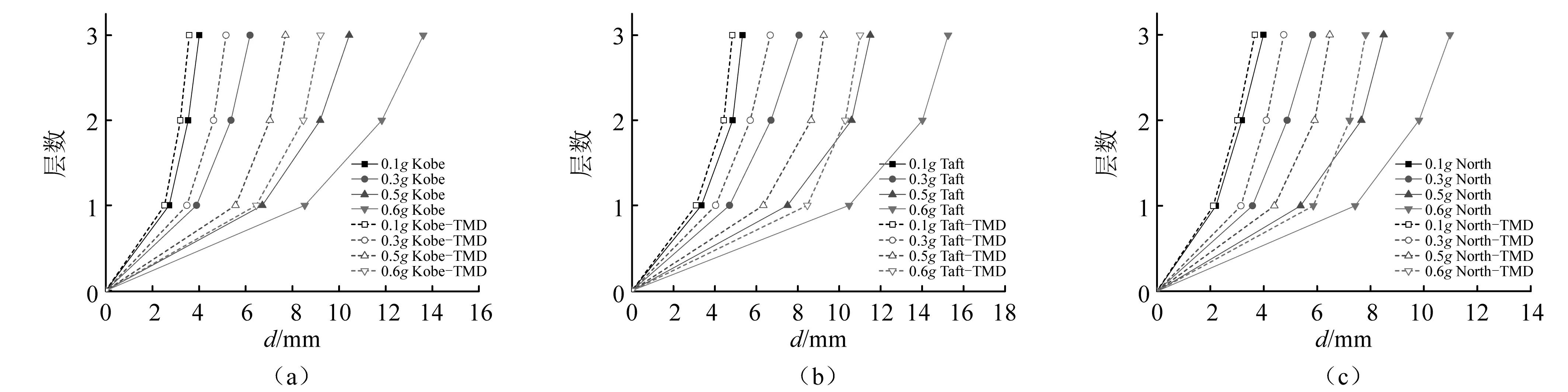
圖11 樓層位移峰值對比圖Fig.11 Comparison of peak displacement of floors

表4 位移減震率對比表Tab.4 Comparison table of displacement damping rate

7 結 論

本文在TMD減震裝置的研究上，設計一種新型裝配墻式減震TMD裝置。將裝置安裝在三層單跨的混凝土框架模型結構中，在三種不同地震波激勵下進行振動臺試驗研究，得出以下結論：

(1)通過對比無控結構和受控結構的傳遞函數，結果表明基于Den Hartog公式優化的TMD安裝后，受控結構傳遞函數幅值明顯小于無控結構。

(2)隨著TMD結構質量比的增大，調諧頻帶逐漸加寬，傳遞函數峰值逐漸減小，但減小程度逐漸放緩，而安裝減震TMD所需的最優參數(剛度、阻尼)均逐漸增加，因此，應結合工況選取合適的質量比，避免材料的浪費。

(3)白噪聲試驗結表明裝有新型裝配墻式減震TMD的結構自振頻率較無控結構有所降低，并延長了結構振動周期。

(4)振動臺試驗結果表明，按最優參數條件下設置的墻式減震TMD，明顯降低了受控結構的動力響應，且隨著地震動峰值的增加，減震裝置的控制效果越發顯著，表明了裝配式構造的合理性和參數優化設計的有效性。

(5)所設計的墻式TMD減震裝置，可充分利用墻體質量，實現減震控制。并且相對于傳統TMD，本文設計的墻式TMD具有節省空間、便于裝拆、配件可更換的優點，具有裝配式建筑的特點，響應我國綠色建筑的號召，具有廣闊的應用前景。

在后續的應用中，應注意墻式TMD位移極限問題，防止墻體與結構發生碰撞，影響減震效果；在后續的研究中，可針對材料非線性問題，進行變阻尼墻式TMD減震裝置的設置，進一步提高減震效果。