分步突破數形解題，教學微設反思探究

李超

［摘? 要］ 二次函數綜合題教學，建議從解法探究、反思探討、方法總結等多視角、多層面展開，引導學生體驗解題過程，總結解題策略. 實際教學時教師可依托“微設計”，幫助學生理解問題，掌握解法，形成解題思維. 文章以2022年蘇州市中考二次函數壓軸題為例，展開解題探究.

［關鍵詞］ 二次函數；幾何；參數；數形結合；微設計

考題探究

1. 考題呈現

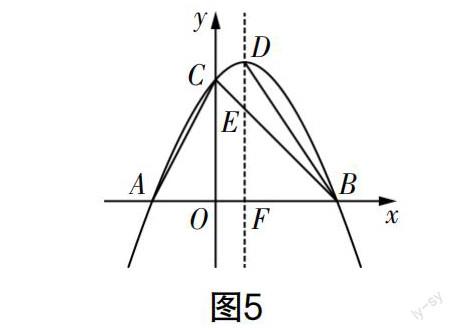
考題（2022年蘇州市中考卷第26題）如圖1所示，二次函數y=-x2+2mx+2m+1（m是常數，且m>0）的圖像與x軸交于A，B兩點（點A在點B的左側），與y軸交于點C，頂點為D. 其對稱軸與線段BC交于點E，與x軸交于點F，連接AC，BD.

（1）求A，B，C三點的坐標（用數字或含m的式子表示），并求∠OBC的度數；

（2）若∠ACO=∠CBD，求m的值；

（3）若在第四象限內二次函數y= -x2+2mx+2m+1（m是常數，且m>0）的圖像上，始終存在一點P，使得∠ACP=75°，請結合函數圖像，直接寫出m的取值范圍.

2. 分步突破

本題為二次函數綜合題，與幾何知識結合緊密. 其中二次函數的解析式中含有參數m，使得函數圖像具有不確定性. 題設三問均圍繞參數m展開，涉及求交點、等角關系轉化、求參數取值范圍等. 解題時建議采用分步突破策略，結合題設構建模型，數形結合地逐一破解.

（1）交點把控，方程破解.

第（1）問求交點坐標及∠OBC的度數. 由題干可知A，B，C三點均為二次函數圖像與坐標軸的交點，所以可通過解方程的方式求得A，B，C三點的坐標.

求點A和點B的坐標：對于y=-x2+2mx+2m+1，令y=0，即-x2+2mx+2m+1=0，可解得x=-1，x=2m+1. 又點A在點B的左側，所以A（-1，0），B（2m+1，0）.

求點C的坐標：對于y=-x2+2mx+2m+1，令x=0，則y=2m+1，所以C（0，2m+1）.

由點B和點C的坐標可知OB=OC，所以△OBC為等腰直角三角形. 所以∠OBC=45°.

另解：實際上，求點A和點B的坐標時，可以采用整合函數式的方式，即把二次函數的解析式轉化為y=-（x+1）［x-（2m+1）］，從而直接得到A（-1，0），B（2m+1，0）.

（2）角度推導，建模分析.

第（2）問設定∠ACO=∠CBD，求m的值，需要從等角關系中推導出參數值，即由“形”到“數”，故需要分析幾何特征，建立幾何與函數之間的關系.

【方法1：從三角函數視角破解】

連接AE，如圖2所示. 因為y=-x2+2mx+2m+1=-（x-m）2+m2+2m+1，所以D（m，m2+2m+1），F（m，0），所以DF=m2+2m+1=（m+1）2，OF=m，BF=m+1. 因為點A和點B關于直線EF對稱，所以AF=BF，∠EAB=∠OBC=45°. 所以△AEB是等腰直角三角形. 所以∠CEA=90°. 因為∠ACO=∠CBD，∠OCB=∠OBC=45°，所以∠ACO+∠OCB =∠CBD+∠OBC，即∠ACB=∠OBD. 所以tan∠ACB=tan∠OBD. 在Rt△AEC中，tan∠ACB==，結合EF∥OC，可進一步得到===；在Rt△FBD中，tan∠OBD==m+1. 從而可得=m+1，解得m=1或m=-1（舍去），所以m的值為1.

【方法2：利用相似三角形的性質破解】

過點D作DH⊥BC，垂足為H，如圖3所示. 由方法1的過程可知DF=（m+1）2，BF=EF=m+1，DE=m2+m. 因為∠DEH=∠BEF=45°，所以DH=EH=DE=（m2+m），BE=BF=（m+1）. 所以BH=BE+EH=（m2+3m+2）. 由∠ACO=∠CBD，∠AOC=∠BHD=90°，可得△AOC∽△DHB，所以=，即=，解得m=1或m=-1. 因為m>0，所以m=1.

（3）數形結合，關系推導.

第（3）問設定∠ACP=75°，求參數m的取值范圍，可采用數形結合的分析方法，把握其中的交點坐標，從而推導參數范圍.

【方法1：由內角和定理推導】

設PC與x軸交于點Q，則點Q總在點B的左側，如圖4所示，此時∠CQA>∠CBA，即∠CQA>45°. 因為∠ACQ=75°，則∠CAO<60°. 所以tan∠CAO<. 在Rt△CAO中，因為tan∠CAO==2m+1，所以2m+1<，解得m<. 又m>0，所以0

【方法2：由角度代換推導】

結合圖像可知∠ACB>∠ACP=75°，因為∠ACB=∠ACO+∠OCB=∠ACO+45°，故只需確保∠ACO>30°即可. 在Rt△CAO中，由tan∠ACO==>，m>0，可解得0

解后探討

上述對一道二次函數綜合題進行了解法探究，其中后兩問為核心之問，分別在設定條件下求m的值或m的取值范圍. 且后兩問均采用兩種方法展開探究，解法具有一定的參考價值，下面進一步總結、思考.

1. 關于第（2）問的解法思考

該問為角相等的條件下參數值的推導，由于問題以二次函數為背景，故明顯具有“數”與“形”的屬性. 上述兩種求解方法的構建思路雖有差異，但總體思路是一致的，即第一步，轉化角度關系，構建線段間的比例關系；第二步，根據線段間的比例關系構建關于線段的參數方程，通過解方程使問題獲解. 但這兩種方法的核心原理不同，“方法1”依據的是“等角的三角函數值相等”，“方法2”則依據“相似三角形的對應邊成比例”. 因此，對于二次函數背景下的等角問題，可采用上述兩種方法破解，具體思路如下.

思路1：三角函數法.

第一步，處理等角關系，將等角條件轉化為三角函數值相等；

第二步，構建三角函數模型，將三角函數值轉化為線段間的比例；

第三步，由三角函數值相等構建方程，通過解方程使問題獲解.

思路2：相似比例法.

第一步，處理等角關系，根據幾何關系提取相似三角形；

第二步，根據相似三角形的特性構建線段的比例；

第三步，根據線段的比例構建方程，通過解方程使問題獲解.

2. 關于第（3）問的解法思考

該問是關于設定角的參數取值范圍問題，需要根據幾何角來推導，上述兩種求解方法均采用了三角函數值轉化方法，只是角度大小關系的推導細節存在差異. 其中“方法1”依據的是三角形的內角和定理，而“方法2”注重角度代換，不過總體思路是一致的. 解決此類問題時，可參考如下步驟：

第一步，數形結合，分析角度大小關系；

第二步，依據三角形內角和定理或進行角度代換，求得核心角的大小取值；

第三步，依托直角三角形，將角度取值轉化為對應三角函數值取值，從而求線段取值范圍或參數取值范圍.

教學微設計

開展試題探究有助于學生強化基礎、融合知識，能培養學生的思維能力，能讓學生養成良好的解題習慣. 在實際教學中，教師可結合試題開展教學微設計，對試題進行拆解、整合，分環節進行教學引導，從而逐步深入問題，使思路自然生成. 下面以上述考題為例，闡述如何進行微設計.

1. 環節1：讀題識圖，鞏固基礎

題設：如圖5所示，二次函數y=-x2+2mx+2m+1（m是常數，且m>0）的圖像與x軸交于A，B兩點（點A在點B的左側），與y軸交于點C，頂點為D. 其對稱軸與線段BC交于點E，與x軸交于點F，連接AC，BD.

設問1：二次函數的圖像與坐標軸有幾個交點？如何求交點的坐標？

設問2：DF所在的直線為二次函數的對稱軸，根據該條件，AF和BF之間存在怎樣的數量關系？

設問3：根據點B和點C的坐標，寫出線段OB和OC之間的數量關系，并判斷△OBC的形狀.

教學引導該環節是對考題第（1）問的拆分引導，教學時教師引導學生求交點坐標，根據坐標值判斷線段之間的長度關系以及三角形的形狀，能讓學生形成“點坐標→線段關系→三角形形狀”的分析思路.

2. 環節2：知識綜合，提升能力

題設：在“環節1”題設的基礎上，過點D作BC的垂線，垂足為H，已知∠ACO=∠CBD.

設問1：根據點的坐標，求DF，BF，DE，DH，BH的長（用含m的式子表示）.

設問2：△AOC和△DHB相似嗎？請說明理由.

設問3：根據△AOC∽△DHB，可以得出怎樣的線段間的比例關系？如何求參數m的值？

教學引導該環節是對考題第（2）問的拆分引導，教學時教師可分三步進行設問. 第一步，根據點的坐標求線段的長；第二步，結合條件證明兩個三角形相似；第三步，利用兩個三角形相似的特性提取線段間的比例關系，構建方程，從而求出參數m的值.

3. 環節3：建模分析，發散思維

題設：在“環節1”題設的基礎上，在第四象限內二次函數y=-x2+2mx+2m+1（m是常數，且m>0）的圖像上，有一點P，連接PC，設PC與x軸交于點Q，點Q總在點B的左側，且始終有∠ACP=75°.

設問1：結合圖像分析∠ACB和∠ACP的大小關系.

設問2：∠ACB=∠ACO+45°，分析∠ACO>30°是否成立.

設問3：在Rt△CAO中，如何表示tan∠ACO？結合“設問2”能否求出m的取值范圍？

教學引導該環節是對考題第（3）問的拆分引導，教學時教師可引導學生利用三角函數知識構建不等式；引導時要注意結合圖像分析幾何角的大小關系，并結合直角三角形模型進行轉化，從而推導出不等關系式.

教學思考

1. 數形分析思路，多解拓展方法

探究二次函數綜合題有助于學生整合知識，提升解題思維. 探究過程建議采用數形結合、多解探討的方式，即教師引導學生讀題、審題、理解函數圖像、構建解題模型，并結合圖像探尋解題思路. 對于綜合型問題，教師要引導學生從不同的視角，采用不同的方法來分析，如上述方法從三角函數、三角形相似的視角來求參數的值. 利用多解探究解題時要側重三點：一是整合并梳理條件，明確關鍵點；二是注重知識回顧、關聯思考；三是讓學生深刻理解不同解題方法的原理.

2. 解后反思過程，教學微設計引導

解后總結方法是解題探究最為關鍵的一環，也是幫助學生提升解題能力的重要環節. 教學時，對于解后反思環節，教師需要從兩個方面來引導學生：一是讓學生回顧解題過程，思考解題方法的特點；二是總結解題方法，生成類型題的解題策略. 在實際教學中，建議教師采用教學微設計的方式拆解復合問題，逐步深入本質，引導學生思考，讓學生體驗解題過程，形成解題思維. 進行微設計時，建議教師從三個方面來展開：一是問題設計呈現難度梯度；二是設問具有引導性、關聯性；三是解題方法直切問題本質，透視問題內涵.

3. 教學滲透思想，注重素養提升

思想方法是解題的精華所在，也是教學的核心內容，解題教學要充分圍繞思想方法展開思路構建，即解題時要滲透數學思想，要在思想的指導下構建解題思路. 如探究二次函數綜合題的過程中，學生可利用模型思想繪制圖像，基于化歸思想轉化、整合條件，基于分類討論思想全面思考問題，基于方程思想構建解題方法，整個解題過程則基于數形結合思想. 教學思想方法時，教師要注重啟發學生思考，并充分圍繞思想內涵進行探討，讓學生參與過程，親身感悟.