教學分析構建課堂，環節精設提升素養

潘琪

［摘? 要］ “一元二次方程”作為初中代數部分的重要知識內容，教學中需要教師深入分析，探索課堂整體構建，基于教學規劃精設教學環節，引導學生完成模型構建、概念生成、知識總結的過程. 教學中教師要以新知傳授、能力提升為教學目標，培養學生的核心素養.

［關鍵詞］ 一元二次方程；模型；概念；一般式；核心素養

“一元二次方程”是蘇科版九年級上冊的重要內容，是一元一次方程的深入推廣，有助于學生解決實際問題，同時能為學生勾股定理、相似等知識的學習提供運算工具. 對于一元二次方程的教學，教師需要把握知識的內在邏輯及聯系，需要對教學內容進行整編重組，需要合理設計教學環節，引導學生探究與思考，從而達到最好的教學效果，下面展開教學探討.

教學分析，課堂整體構建

“一元二次方程”的章節內容安排在九年級上冊，此時學生已經掌握了一元一次方程、二元一次方程組等知識，感受到了方程作為刻畫現實中數量關系的有效模型的價值和作用，同時積累了利用方程求解問題的方法和經驗. 教學“一元二次方程”時，教師需要圍繞三大重點開展教學引導：一是引導學生探索實際問題中的數量關系、變化規律，從問題中抽象出一元二次方程，使學生感受模型；二是一元二次方程的概念是教學的重點，需要學生通過觀察，歸納和總結出一元二次方程的概念；三是對于一元二次方程的形式及特點，需要教師引導學生關注方程的二次項、一次項及常數項.

對于一元二次方程的教學過程，建議教師有效設計教學環節，重視知識的整體設計，以及學生核心素養的培養. 故教學中需要教師把握學情，尊重學生的主體地位，引導學生經歷一元二次方程的建模過程、概念的生成過程，深刻理解其一般式的形成過程，同時培養學生的數學建模素養、抽象轉化素養，提升學生的數學運算能力、邏輯推理能力等.

教學“一元二次方程”時，建議教師圍繞“列”“納”“究”三個字開展一元二次方程的抽象建模、概念生成、形式歸納過程. “列”，即呈現實際問題，引導學生分析數量關系，開展建模教學；“納”，即引導學生從式、元、次三方面對方程進行探討，歸納一元二次方程的概念；“究”，即引導學生關注一元二次方程，總結特征，掌握形式，把握方程的一次項、二次項和常數項.

設計環節，核心素養提升

基于上述教學分析及整體構建，建議教師按照“實例抽象，構建方程→觀察辨析，方程定義→方程探究，知識總結”這條主線來開展教學，其中，教學根據實際問題中的數量關系列方程時，滲透建模思想；進行概念教學時，注重提升學生的歸納、概括能力；在方程的提取與轉化中提升學生的辨析能力和運算能力. 下面圍繞主線具體探究.

1. 構建方程，數學建模

【環節1：情境感悟，提煉關系】

教學中，教師應結合常見的情境問題，讓學生關注其中的數量關系，從而列出方程.

例1：一個正方形的邊長增加2 cm后，所得的新正方形的周長為28 cm，求原正方形的邊長.

例2：一正方形桌面的面積為2 m2，求正方形桌面的邊長.

教學引導教師引導學生根據問題設出未知數，列出方程，分析所列方程的特點，引發學生的認知沖突，為后續一元二次方程的探究做鋪墊. 對于例1，設原正方形的邊長為x cm后可列出方程4（x+2）=28；對于例2，設正方形桌面的邊長為x m后，可列出方程x2=2.

【環節2：深入探究，方程構建】

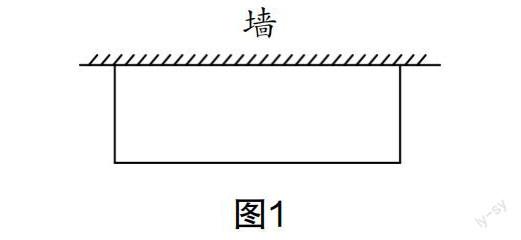
例3：如圖1所示，矩形花圃的一邊靠墻，另外三邊用柵欄圍起來. 已知所用柵欄的總長為19 m，花圃的面積為24 m2.

預設問題：（1）若設與墻相鄰的一條邊的長為x m，怎么表示與墻相對的一條邊的長？（2）根據花圃的總面積，如何構建方程？

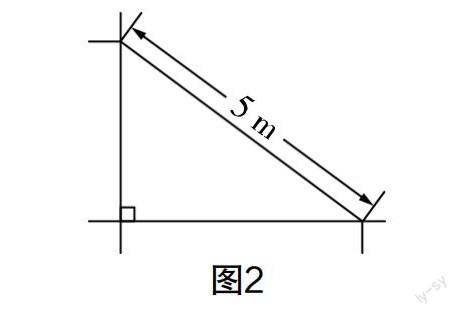
例4：如圖2所示，長為5 m的梯子斜靠在墻角，已知梯子的底端到墻的距離比梯子的頂端到地面的距離多1 m.

預設問題：（1）設梯子的底端到墻面的距離為x m，怎么表示梯子頂端到地面的距離？（2）如何根據數量關系列方程？

例5：已知某學校圖書館的藏書在兩年的時間里，由5萬冊增加到了9.8萬冊.

預設問題：（1）設該學校圖書館的年藏書增長百分率為x，則一年后該學校圖書館的藏書為多少萬冊？（2）兩年后該學校圖書館的藏書為多少萬冊？

教學引導教學時，教師引導學生設未知數，根據條件推導變量，結合數量關系構建方程. 對于例3，可列出方程x（19-2x）=24；對于例4，可列出方程x2+（x-1）2=52；對于例5，可列出方程5（1+x）2=9.8.

2. 形式提取，定義方程

【環節1：觀察辨析，發現特征】

在該環節，教師引導學生對比觀察上述問題中所列的方程，引導學生發現方程的特征.

問題：觀察上述所列方程，即4（x+2）=28，x2=2，x（19-2x）=24，x2+（x-1）2=52，5（1+x）2=9.8，你發現了什么？它們在形式上有什么共同點？

教學引導教學時，特征探索環節可按照“變形→比較→分析”的方式進行分步引導，即教師先讓學生變形上述方程，且要求將方程變形為等號右邊是0的形式；然后讓學生觀察方程的未知數，包括未知數的個數、次數及項式；最后引導學生發現后面四個方程含有二次項，有別于之前所學的一元一次方程.

【環節2：歸納總結，概念生成】

該環節需要教師引導學生從式、元、次三個維度對一元二次方程下定義.

預設問題：（1）針對2x2-2x-24=0，思考該方程的一般形式；（2）根據對應的一般形式概括一元二次方程的概念.

教學引導教師引導學生根據方程概括一元二次方程的一般形式，即ax2+bx+c=0（a≠0），然后對一元二次方程進行定義，即等號兩邊均為整式，只含有一個未知數，且未知數的最高次數為2的方程. 教學中教師可以按照如下方式進行細化：式→等號兩邊均為整式；元→只含有一個未知數；次→未知數的最高次數是2.

【環節3：辨析方程，深刻理解】

定義完一元二次方程的概念后，教師應引導學生針對一元二次方程的一般式展開辨析，尤其是其中的特征參數a，應從a≠0和a=0兩方面進行辨析與思考.

思考問題：針對一元二次方程ax2+bx+c=0（a≠0）中的二次項系數a，思考為什么要強調a≠0. a是否可以等于0？

教學引導教師引導學生深刻理解一元二次方程的隱含條件，采用“假設→否定”的方式，即假設二次項系數a=0，則方程變為bx+c=0，此時方程不再是一元二次方程，從而把握住一元二次方程與一元一次方程本質的不同.

3. 方程探究，知識總結

該環節需要教師引導學生探究一元二次方程的一般形式，并理解方程的二次項、一次項和常數項，準確識別一次項系數和二次項系數. 教學中教師可以給出具體的方程，引導學生按照“一般式變形→化簡降次排序→項式整理”的方式來進行.

例6：已知方程x2+3x=8，2x2=3x，3x2=27，5（1+x）2=7.

設問：按照如下步驟對方程進行整理. 步驟1，化簡方程，將其變形為一般式；步驟2，將方程的各項按照未知數降次的順序排列；步驟3，整理各方程的二次項、一次項和常數項.

教學引導教師讓學生將各方程化簡為一般式，即化簡為ax2+bx+c=0（a≠0）的形式，指導學生明晰一般式中ax2，bx和c分別是方程的二次項、一次項和常數項，其中a是二次項的系數，b是一次項的系數. 在此基礎上，教師結合具體方程展開解題分析.

總結探究時，教師要引導學生明晰定義，掌握方程一般式的轉化技巧，提升學生的數學語言能力. 而在變形探究中，建議教師結合多類型的方程，幫助學生強化一元二次方程的定義，培養學生的邏輯推理能力.

教學思考，課堂教學建議

1. 問題引領，追問引導推進

課堂教學應是探究式、開放式的，建議教師采用知識探究的方式，圍繞教學核心，精設環節，以問題為引導驅動課堂. 故對于一元二次方程的教學，教師應引導學生參與課堂活動，通過設置問題進行師生對話互動，引導學生抽象出數學模型，明晰一元二次方程的定義，掌握一元二次方程的一般式，能準確識別出方程的項式及對應的系數. 問題預設則要遵循學生思維發展規律和認知規律，符合知識生成過程，培養學生的邏輯思維能力.

2. 立足教學，核心素養發展

新知的探究教學，兼具兩大目標：一是引導學生掌握新知；二是提升學生能力，發展核心素養. 其中后者也是教學的最終目標. 在“一元二次方程”這一章，教師需要立足教學環節，開展核心素養培養，包括數學建模、抽象概括、推理運算等. 故教學中教師需要借助知識，在探究環節滲透數學思想，讓學生感知數學思想，提升學生的數學思維. 如指導學生從實例中抽象出數學模型，在定義中培養學生的歸納、總結能力，借助方程的一般式變形來培養學生的數學運算素養.