把握方法技巧 解答電磁學習題

葉麗香

摘 要：電磁現象是自然界中非常常見的一種現象，同時也是高中物理學科中的重要知識內容.電磁學知識內容較為抽象，學習和理解的難度比較大，學生常常會出現困惑和疑問，對于一些物理問題常常無從下手，影響學生解題效果，不利于學生解題能力培養.在高中物理教學中，為了加強學生解題能力鍛煉，強化學生解題思維，掌握解題方法和技巧，結合實際的電磁學解題，開展解題方法講解和訓練.本文分析高中物理電磁學解題的有效方法.

關鍵詞：高中物理;電磁學;解題方法

中圖分類號：G632?? 文獻標識碼：A?? 文章編號：1008-0333（2022）25-0122-03

電磁學作為高中課程的重要內容，不僅涉及到電流現象、電磁輻射和電磁場等知識，同時電磁學知識和動能、勢能等知識密切相關.雖然電磁學知識內容較為抽象，通過課堂教學要求學生掌握電磁學基本原理，合理利用解題方法，對典型題目進行歸納和總結，靈活掌握和利用解題方法，保證電磁學問題有效解答.因此，在課堂活動中，傳授學生科學的解題方式，加強學生解題思維和解題能力培養，提高學生知識應用能力.

1 巧妙利用圖像法，化抽象為具體

高中物理電磁場解題中，圖像法是一種有效的解題方式，具有直觀形象的優勢，借助一個或者多個圖形，將物理問題展示出來，根據其中的幾何關系，將抽象物理問題轉化成具體圖形，有效解答題目.在電磁場知識學習中，引導學生不斷歸納和總結，結合知識點特點引入圖像法，降低題目解答難度，提高學生解題效率，保證學生解題準確性.

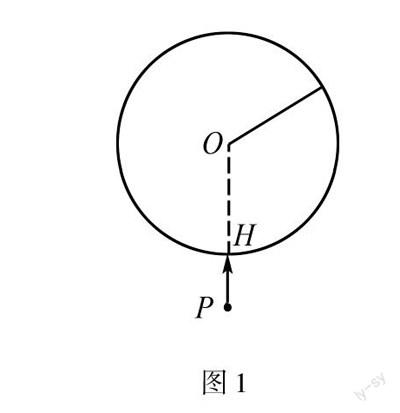
例1 如圖1所示，圓形筒橫截面中，O是軸線，R是半徑，在圓筒內部存在勻強磁場，并且與圓筒的軸線平行.如果B是磁感應強度，H點是真空狀態下的小孔.帶電粒子p的質量為m，q是其電荷量，以某個初速度進入圓筒內部，并且和圓筒碰撞，從小孔處射出.圓筒內部光滑，碰撞存在彈性.當p的速度是多少時，p和圓筒內壁碰撞次數最少，從進入圓筒到射出的時間是多少？

解析 通過對題目進行分析，可以得出此題主要是利用洛倫磁力解答的題目，可以采取圖像法完成解題.如果說P和筒壁僅僅碰撞一次，那么p是直線運動，根據題干內容分析，p和圓筒內壁碰撞不止一次.在圓筒內部有著勻強磁場，P由于洛倫磁力的影響，發生一定的偏轉，p和圓筒內壁之間碰撞屬于彈性碰撞，在發生碰撞的前后，其速度大小沒有發生改變，結合圓筒內壁形狀進行猜想，P和筒壁碰撞出現對稱情況.在解題時，以幾何圖形分析作為突破點，找出圓的三等分點，結合受力情況對P運動軌跡進行描述，根據其幾何關系完成求解.

2 靈活利用微元法，化宏觀為微觀

微元法主要是將研究對象作為整體中的微小部分，通過對這一微小部分和整體關系進行分析和研究，完成整體問題的思考和解答.在高中物理解題中，微元法雖然使用的比較少，卻是一種重要的物理思想.在高中電磁場相關題目解答中，靈活引入微元法，將復雜物理問題轉化成常見的物理規律，將非理想物理模型轉化成學生熟悉的理想模型，實現宏觀問題微觀化的轉化，完成物理問題的思考和解答.

3 利用等效代替法，簡化解題過程

高中物理電磁學解題中，一些物理題目具有一定的共性，利用共性完成解題，因此，面對一些物理問題，可以采取等效代替的方式解答，將復雜物理問題轉化成熟悉問題.在等效替代前，需要進行物理量的比較，尋找物理量的相同點，有效解決共性問題，提高學生解題速度，保證學生解題準確性.

例2 如圖2所示，三角形MKN屬于等邊三角形，且是由均勻細導線制作，在均勻恒定磁場中，磁感應強度是B，三角形MKN以MN為軸線以角速度為ω做轉動運動，MN和磁場方向垂直，并且三個線框電阻是R，圖中線框位置剛好是t=0.求解（1）任意時刻t線框中的電流;（2）假設M點的電動勢是0，則MK線框上任意一點A在t=0時的電動勢是多少？

解析 通過分析題意得出，在解題時，利用法拉第電磁感應定律，求解三角形切割磁感線產生的電動勢.因為MN和磁感線垂直，另外兩條邊和磁感線不垂直，在磁感線切割時，其投影長度是有效長度，為dcos60°，如圖3.通過這樣的方式，將題目進行轉化，求解出垂直磁感應強度B方向，長度是d，距離MN軸距離為12dcos60°的導向產生的電動勢就可以.借助這樣的等效替代方式，將復雜電磁場問題轉化簡單問題，完成物理問題的有效解答.4 借助守恒轉化法，明確解題思路

高中物理電磁學解題中，借助守恒定律轉化物理問題，讓學生掌握更多解題思路.作為高中物理教師，有效利用守恒轉換的方式，簡化高中物理解題，有效解決物理問題.在守恒定律的利用中，可以通過能量守恒、質量守恒和電荷守恒等，對復雜問題進行轉化，從不同角度思考問題，明確解題思路，強化學生解題能力，提高學生解題效率.

例3 一個均勻絕緣的細圓環的質量是m，半徑是R，在其上均勻分布一個帶電量為q的正電荷.當對其施加外力后，圓環圍繞圓心與環面垂直的中心線做勻速轉動.圓環從靜止到運動過程中，當角速度達到ω0時，一共做了多少功.

解析 在解題時，需要對題目進行分析，由于外力的方向與大小在不斷變化，因此，做的功也處于變化中，按照這樣的方式求解，其過程非常復雜，計算也較為困難.因此，教師可以引導學生從其他方面入手，尋找其他解題思路，對其進行綜合分析，得出做功的本質是能量的轉化，求解外力做功后轉化的能量，完成做功綜合求解.

5 運用數學知識，構建參數關系

數學知識與物理有著密切的聯系，因此在解答電磁感應相關習題時應提高數學知識應用意識，結合習題創設的情境積極聯系所學的數學知識、數學結論，構建數學知識與物理問題之間的內在聯系.教學實踐中應注重給學習者預留空白時間，先要求其根據題意嘗試著運用數學知識進行分析，思考解題需要運用哪些數學知識.當學習者一時難以找到解題思路時應注重運用多媒體技術化抽象為直觀，降低解題難度，增強解題自信.

例4 在真空中存在一棱長d=6cm的正四面體，頂點為分別為ABCD.該四面體處在勻強電場中，電場方向平行于ABD平面.若A、B和C點的電勢分別為（2-6）V，（2+6）V和2V.則該四面體的外接球面上電勢最低值、最高值分別為（ ?）.

A.-1V、5V??? B.0、5V

C.（2-23）V、（2+23）V

D.（2-22）V、（2+22）V

解析 根據題意畫出如圖4所示圖形，由勻強電場與等勢面之間的關系，設O為AB的中點O1，該點電勢為2V.CO2和電場線垂直，因此，C點電勢為2V，則平面O1CD為等勢面，BA和電場線平行，方向沿BA，電場強度大小為E=UBA/d=200V/m.由數學知識可知正四面體的外接球半徑R=6d/4=1.5cm，ΔU=ER=3V.球心O點的電勢為2V，則正四面體的外接球面上的最低電勢和最高電勢分別為：φO-ΔU=-1V.φO+ΔU=5V，綜上選擇A項.

6 運用平衡狀態，尋找解題思路

高中物理部分電磁學習題創設的情境較為復雜，難度不盡相同，解題的思路也多種多樣.實踐中應注重啟發學習者樹立解題的自信心，通過認真審題尋找解題的蛛絲馬跡.實踐表明運用物體所處的平衡狀態，構建相關的平衡方程是求解未知參數的重要思路.為提高學習者解題的正確性，解題時應做好物體在不同運動情形中的受力分析，并根據題干中給出的關鍵詞，如“剛好”、“恰好”等，構建平衡方程，實現習題的順利突破.例5

如圖5，間距為L光滑足夠長的金屬導軌和水平面呈θ=30°固定，虛線ab、cd均和導軌垂直，在其和導軌圍成的矩形區域內存在垂直導軌平面向上，磁感應強度大小為B的勻強磁場.將PQ、MN兩根質量均為m，阻值均為R的金屬棒靠在一起置于導軌上.釋放PQ當其到達ab瞬間，再將MN釋放.PQ進入磁場后做勻速運動，PQ到達cd時MN剛好到達ab.忽略導軌電阻，重力加速度為g，則MN通過磁場過程中，PQ上產生的焦耳熱為.

解析

在高中教學中，物理學科有著重要的地位，也是學生學習困難的學科.電磁學是高中物理課堂的重要內容，也是學生解題中的難點內容，因此，應當重視學生解題教學，幫助學生掌握解題方法，強化學生物理解題思維訓練.在實際的解題教學中，結合典型例題進行歸納和總結，讓學生掌握多種解題方法，靈活利用物理原理和思維，結合題目特點采取解題方法，提高學生解題效率和質量.

參考文獻：

[1]沈軍.高中物理電磁學的解題方法研究[J].數理化解題研究，2021（25）：85-86.

[2] 祁紅菊.巧設微專題，提升教材習題的應用價值——以“電磁感應：單棒切割問題”為例[J].物理教師，2020，41（08）：83-85.

[3] 黃蕊，趙健坤，潘蘇東.高中物理電磁學認知診斷研究[J].物理教學，2019，41（10）：28-32.

[4] 張宇軒.關于高中電磁學的解題方法研究[J].科技資訊，2018，16（26）：228+230.

[5] 蔡亮.多解分析與變式教學的目標、鋪墊和遷移——以一節“電磁感應”習題課為例[J].物理教學，2018，40（02）：15-16+40.

[6] 唐博海.高中物理電磁學習題解答困難的解決對策[J].低碳世界，2017（36）：373-374.

[責任編輯：李 璟]