小學數學說理能力培養策略

蘭伏聲

小學數學說理能力的培養對學生獲得課堂新知、培養邏輯思維能力具有重要意義。圍繞培養說理能力開展的相關課堂實踐活動，必須滲透在教師數學課堂教學實踐中，以促進學生知理、明理。

一、通過問題引領學生說理

數學課堂應重視知識的形成過程，利用學生已有的生活經驗、知識基礎、認知結構，以有效活動為支撐，通過問題引領、對話交流對數學知識進行思辨提升、追根溯源，引導學生挖掘那些隱藏在數學知識背后的深層次的數學之“理”，從而促進學生對數學知識的理解，活化數學思維。

例如，在教學蘇教版二下“兩、三位數的加法和減法”時，教師以算式“375+986”為例，提出問題：“為什么整數加法一定要從個位加起？請一位同學嘗試說說這道題能不能從高位加起呢。”在學生以往“100以內的加法和減法”的知識架構中，加法都是從個位加起的，教師引導學生進行逆向推導的說理過程，試圖驗證“從個位加起”的合理性。學生嘗試把這個說理過程表達出來：“在算式375+986中，先把百位上的3和9相加等于12，再把十位上7與8相加等于15，發現15還要往百位上進個1，原來的12就要改寫成13，最后個位上的5和6相加得11，要往十位進一，原來十位上的5要改寫成6。”教師總結：“從高位加起需要對得數進行反復改寫，所以要從個位加起。”通過這樣的說理過程，學生得出結論：從個位加起更方便、快捷，省去反復進位和改寫的麻煩。從而使學生明白教師為什么在做加法或者減法計算題時反復強調應從個位開始計算。在課堂教學中有意識地培養學生說理能力，使他們能夠條理清晰地進行數學語言的表達，數學的邏輯思維得到強化。在說理過程中讓學生圍繞核心問題進行積極思考，并且重視說理的思維過程，以及對說理方向的引導和把控。

二、通過對比引導學生說理

數學是一門講道理的學科，數學學科的定理、法則、算理等知識的產生、發展及每個規則的確定都蘊含著深刻的數學道理。教師可通過對相似概念、算理的對比，進行更好地區分，并揭示其本質，幫助學生更易于記憶和掌握。

例如，在教學蘇教版五下“小數加減法”時，由于學生不明白小數加減法豎式計算中為什么一定要小數點對齊，而不是像整數加減法豎式計算只要末位對齊，由此確定本節課的重難點“小數加減法豎式計算時應注意小數點對齊”，教師出示以下例題并列出的豎式，以供學生更好地進行對比。

例1：19.8+65.6=????? ????????????例2：16.87+1.983=

對例1、例2所列豎式進行觀察、對比，引導學生進行充分表達：“19.8加65.6可以小數點對齊，也可以末位對齊;16.87加1.983只能小數點對齊，卻不能末位對齊，16.87的末位7是在百分位上，而1.983的末位3是在千分位上，末位的3和7是兩個不相同的數位，因此不能對齊相加。”再與“整數加減法”的前置知識進行對比，點出為何整數加減可以末位對齊，而小數加減不能，再次引導學生充分表達：“由于整數加減法計算中末位都是個位，所以末位對齊就是等同于相同的數位對齊;而在小數加減法計算中，小數點右邊的位數可能不一致，比如16.87是兩位小數，1.983是三位小數，這樣只有小數點對齊了，才能保證相同的數位對齊，而末位對齊并不能保證相同的數位一定會對齊。”最后，教師提出問題：“整數加減法和小數加減法的相同點是什么？”學生得出結論：“整數和小數加減法的相同點就是相同數位要對齊。”至此，教師通過層層遞進的引導教學，使學生實現充分的觀察、對比、表達，培養學生的說理能力，使學生對小數和整數加減法計算的本質有了更深刻的理解。

三、創造機會為學生提供說理平臺

教師開展說理活動，可以更好地了解學生對課堂知識的掌握情況。教師可在下節課前預留3分鐘針對上節課的內容開展說理展示活動，引導學生在理解的基礎上模仿教師的授課方式對知識點進行梳理。先安排學有余力的學生進行說理，運用優秀學生的榜樣示范作用帶動其他學生積極參與，讓學生能夠通過說理發現學習數學的樂趣，從而能夠更好地掌握和理解數學知識點，得到良好的課堂教學效果。也可在課后布置與說理有關的家庭作業，使學生的整理、歸納、提煉能力得到更好的發展。

以蘇教版五下“圓”的面積教學為例，在該單元中圓的面積公式推導是個難點，如何把一個圓的面積轉化成近似平行四邊形的面積，還要縷清轉化后近似平行四邊形的底、高和圓的半徑之間的聯系，從而推導出圓的面積計算公式。教師引導學生動手操作，把圓沿著半徑進行折一折、剪一剪，將其分成若干個扇形，然后重新拼成一個近似的平行四邊形。教師請一位學生把圓剪拼成近似平行四邊形的過程演示出來，并讓他進行即興說理：“通過把圓進行切割和拼接，使這個圓變成了一個近似的平行四邊形，那么要求原來圓的面積，只要求出這個近似的平行四邊形的面積即可。平行四邊形的底就是原來圓的周長的一半，高為圓的半徑，所以S=1/2×2πr×r=πr?。”在此過程中，同伴的表達讓各個層面的學生更容易理解及鞏固新知識，也使學生的關注度和興趣度得到更有效的提升。

四、運用多種手段推動學生說理

推理意識是小學階段數學核心素養之一，推理一般包括合情推理和演繹推理。依據小學階段學生的思維發展水平以及新課標中對小學數學的學習要求，主要以合情推理為主。隨著學生的年齡增長，說理的要求應從低、中段大膽、簡單的數學說理表達，到高段運用完整、嚴謹的數學語言進行說理，學生在說理時的邏輯思維逐漸得到發展。另外，教師應根據學生說理的優點和不足進行點評，還可以提供本節課的微課視頻讓學生觀摩，引導學生不斷改進說理方法，提升他們的推理意識。

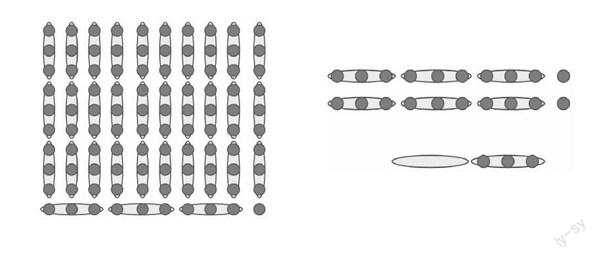
邏輯思維如何通過數學說理的方式得以展示呢？以蘇教版五下“因數與倍數”中“3的倍數特征”的課堂教學為例，筆者引導學生運用數形結合的方式進行表述，使其他學生更易于理解。以“驗證123這個數字是否為3的倍數”為例，借助了課件中的圖形演示來協助說理（如下圖）。學生在課件上邊比劃邊說理：“可以把123個點子分成了100+20+3，對100個點子3個3個地分，最后剩下1個，20個點子也是3個3個地分，最后剩下了2個，百位剩下的1個和十位剩下的2個合起來是3個，加上個位上的3個一共6個，是3的倍數，因此123是3的倍數。”教師引導學生借助數形結合的方式進行說理，最終總結：3的倍數特征是各個數位上的數字加起來的和是3的倍數。

（作者單位：福建省福安市實驗小學陽泉校區?????? 責任編輯：宋曉穎）