1.全國高考甲卷?理科

一、選擇題

1.若z=-1+3i，則zz-1=（）

（A）-1+3i.（B）-1-3i.

（C）-13+33i.（D）-13-33i.

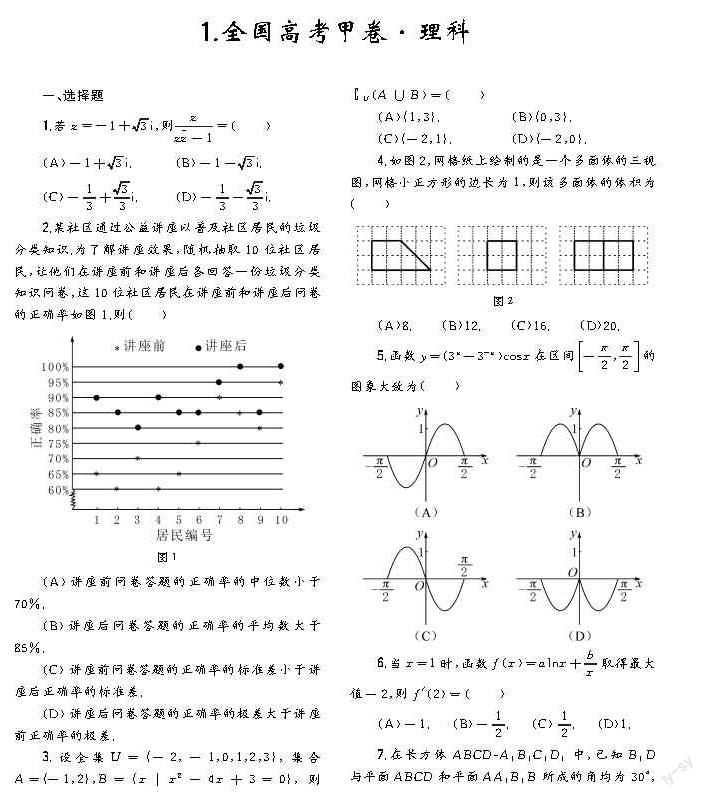
2.某社區通過公益講座以普及社區居民的垃圾分類知識.為了解講座效果，隨機抽取10位社區居民，讓他們在講座前和講座后各回答一份垃圾分類知識問卷，這10位社區居民在講座前和講座后問卷的正確率如圖1.則（）

（A）講座前問卷答題的正確率的中位數小于70%.

（B）講座后問卷答題的正確率的平均數大于85%.

（C）講座前問卷答題的正確率的標準差小于講座后正確率的標準差.

（D）講座后問卷答題的正確率的極差大于講座前正確率的極差.

3.設全集U={-2，-1，0，1，2，3}，集合A={-1，2}，B={x|x2-4x+3=0}，則瘙綂U（A∪B）=（）

（A）{1，3}.（B）{0，3}.

（C）{-2，1}.（D）{-2，0}.

4.如圖2，網格紙上繪制的是一個多面體的三視圖，網格小正方形的邊長為1，則該多面體的體積為（）

（A）8.（B）12.（C）16.（D）20.

5.函數y=（3x-3-x）cosx在區間-π2，π2的圖象大致為（）

6.當x=1時，函數f（x）=alnx+bx取得最大值-2，則f′（2）=（）

（A）-1.（B）-12.（C）12.（D）1.

7.在長方體ABCD|A1B1C1D1中，已知B1D與平面ABCD和平面AA1B1B所成的角均為30°，則（）

（A）AB=2AD.

（B）AB與平面AB1C1D所成的角為30°.

（C）AC=CB1.

（D）B1D與平面BB1C1C所成的角為45°.

8.沈括的《夢溪筆談》是中國古代科技史上的杰作，其中收錄了計算圓弧長度的“會圓術”.如圖3，AB是以O圓心，OA為半徑的圓弧，C是AB的中點，D在AB上，CD⊥AB.“會圓術”給出AB的弧長的近似值s的計算公式s=AB+CD2OA.當OA=2時，∠AOB=60°時，s=（）

（A）11-332.（B）11-432.

（C）9-332.（D）9-432.

9.甲、乙兩個圓錐的母線長相等，側面展開圖的圓心角之和為2π，側面積分別為S甲和S乙，體積分別為V甲和V乙.若S甲S乙=2，則V甲V乙=（）

（A）5.（B）22.（C）10.（D）5104.

10.橢圓C：x2a2+y2b2=1（a>b>0）的左頂點為A，點P，Q均在C上，且關系y軸對稱.若直線AP，AQ的斜率之積為14，則C的離心率為（）

（A）32.（B）22.（C）12.（D）13.

11.設函數f（x）=sinωx+π3在區間（0，π）內恰有三個極值點、兩個零點，則ω的取值范圍是（）

（A）53，136.（B）53，196.

（C）136，83.（D）136，196.

12.已知a=3132，b=cos14，c=4sin14，則（）

（A）c>b>a.（B）b>a>c.

（C）a>b>c.（D）a>c>b.

二、填空題

13.設向量a，b的夾角的余弦值為13，且|a|=1，|b|=3，則（2a+b）·b=.

14.若雙曲線y2-x2m2=1（m>0）的漸近線與圓x2+y2-4y+3=0相切，則m=.

15.從正方體的8個頂點中任選4個，則這4個點在同一平面的概率為.

16.已知△ABC中，點D在邊BC上，∠ADB=120°，AD=2，CD=2BD，當ACAB取得最小值時，BD=.

三、解題答

17.記Sn為數列{an}的前n項的和.已知

2Snn+n=2an+1.

（1）證明：{an}是等差數列;

（2）若a4，a7，a9成等比數列，求Sn的最小值.

18.在四棱錐P|ABCD中，PD⊥底面ABCD，CD∥AB，AD=DC=CB=1，AB=2，DP=3.

（1）證明：BD⊥PA;

（2）求PD與平面PAB所成的角的正弦值.

19.甲、乙兩個學校進行體育比賽，比賽共設三個項目，每個項目勝方得10分，負方得0分，沒有平局.三個項目比賽結束后，總得分高的學校獲得冠軍.已知甲學校在三個項目中獲勝的概率分別05，04，08，各項目的比賽結果相互獨立.

（1）求甲學校獲得冠軍的概率;

（2）用X表示乙學校的總得分，求X的分布列與期望.

20.設拋物線C：y2=2px（p>0）的焦點為F，點D（p，0），過F的直線交C于M，N兩點.當直線MD垂直于x軸時，|MF|=3.

（1）求C的方程;

（2）設直線MD，ND與C的另一個交點分別為A，B，記直線MN，AB的傾斜角分別為α，β.當α-β取得最大值時，求直線AB的方程.

21.已知函數f（x）=exx-lnx+x-a.

（1）若f（x）≥0，求a的取值范圍;

（2）證明：若f（x）有兩個零點x1，x2，則x1x2<1.

22.（選修4-4：坐標系與參數方程）

在直角坐標系xOy中，

曲線C1的參數方程為x=2+t6，y=t（t為參數），

曲線C2的參數方程為x=-2+s6，y=-s（s為參數）.

（1）寫出C1的普通方程;

（2）以坐標原點為極點，x軸正半軸為極軸建立極坐標系，曲線C3的極坐標方程為2cosθ-sinθ=0，求C3與C1交點的直角坐標，及C3與C2交點的直角坐標.

23.（選修4-5：不等式選講）

已知a，b，c均為正數，且a2+b2+4c2=3.

（1）證明：a+b+2c≤3;

（2）若b=2c，則1a+1c≥3.

參考答案

題號12345678910答案CBDBABDBCA

題號111213141516答案CA11336353-1

17.（1）由于2Snn+n=2an+1，

變形為2Sn=2nan+n-n2，①

又2Sn-1=2（n-1）an-1+n-1-（n-1）2，②

①-②，得（2n-2）an-（2n-2）an-1=2n-2，

n≥2，n∈N*，

即an-an-1=1，n≥2，n∈N*，

所以{an}是等差數列.

（2）由題意可知a27=a4a9，

即（a1+6）2=（a1+3）（a1+8），

解得a1=-12，

所以an=-12+（n-1）×1=n-13，

其中a1

故Sn的最小值為S12=S13=-78.

18.（1）因為PD⊥底面ABCD，

所以PD⊥BD.

取AB中點E，連接DE，

可知DE=12AB=1.

因為CD∥AB，

所以CD瘙綊BE，

四邊形BCDE為平行四邊形，

故DE=CB=1.

又DE=12AB，

所以△ABD為直角三角形，

AB為斜邊，

故BD⊥AD.

又PD∩AD=D，

所以BD⊥平面PAD，

故BD⊥PA.

（2）由（1）知

PD，AD，BD兩兩垂直，

BD=AB2-AD2=3.

如圖6，建立空間直角坐標系，則

D（0，0，0），A（1，0，0），

B（0，3，0），P（0，0，3），

所以PD=（0，0，-3），

PA=（1，0，-3），

AB=（-1，3，0）.

設平面PAB的法向量為

n=（x，y，z），

則PA·n=0，AB·n=0，即x-3z=0，-x+3y=0，

不妨設y=z=1，則n=（3，1，1）.

設PD與平面PAB的所成角為θ，則

sinθ=|cos〈PD，n〉|=|PD·n||PD|·|n|

=|-3|3×5=55，

所以PD與平面PAB的所成的角的正弦值為55.

19.（1）記甲學校獲得冠軍為事件A，則

P（A）=05×04×（1-08）+

05×（1-04）×08+

（1-05）×04×08+

05×04×08

=06，

所以甲學校獲得冠軍的概率是06.

（2）X的可能取值為0，10，20，30，

則P（X=0）=05×04×08=016，

P（X=10）=05×04×（1-08）+

05×（1-04）×08+

（1-05）×04×08

=044，

P（X=20）=05×（1-04）×（1-08）+

（1-05）×（1-04）×08+

（1-05）×04×（1-08）

=034，

P（X=30）=（1-05）×（1-04）×（1-08）

=006，

X的期望值E（X）

=0×016+10×044+20×034+30×006

=13.

20.（1）由題可知

當x=p時，y2=2p2，

則yM=2p，

可知|MD|=2p，|FD|=p2.

在Rt△MFD中，

|FD|2+|DM|2=|FM|2，

得p22+（2p）2=9，即p=2，

故C的方程為y2=4x.

（2）要使α-β最大，則tan（α-β）最大，且易知當直線MN的斜率為負時，α-β為正才能達到最大.

又tan（α-β）=tanα-tanβ1+tanαtanβ.

設M（x1，y1），N（x2，y2），

A（x3，y3），B（x4，y4），

由（1）知F（1，0），D（2，0），

則tanβ=kMN=y1-y2x1-x2=y1-y2y214-y224=4y1+y2.

又N，D，B三點共線，

則kND=kBD，y2-0x2-2=y4-0x4-2，

y2-0y224-2=y4-0y224-2，

y2y4=-8，y4=-8y2.

同理由M，D，A三點共線可得y3=-8y1，

則tanα=4y3+y4=y1y2-2（y1+y2），

由題可知，直線MN斜率不為0，

不妨設lMN：x=my+1（m<0）.

由y2=4x，x=my+1，得

y2-4my-4=0，

即y1+y2=4m，y1y2=-4，

則tanβ=44m=1m，tanα=-4-2×4m=12m，

tan（α-β）=12m-1m1+12m·1m=-12m+1m，

可知當m=-22時，tan（α-β）最大，即α-β最大，

此時AB的直線方程為

y-y3=4y3+y4（x-x3），

即4x-（y3+y4）y+y3y4=0.

又y3+y4=-8y1+-8y2=-8（y1+y2）y1y2

=8m=-42，

y3y4=-8y1·-8y2=-16，

則AB的直線方程為

4x+42y-16=0，

即x+2y-4=0.

21.（1）f（x）定義域為（0，+∞），

f′（x）=ex（x-1）x-1x+1

=（ex+x）（x-1）x.

令f′（x）=0，得x=1，

所以0

當x>1時，f′（x）>0，f（x）單調遞增，

所以f（x）min=f（1）=e+1-a，

要使得f（x）≥0恒成立，即滿足

f（x）min=f（1）=e+1-a，

所以e+1≥a.

（2）由（1）知要使得有f（x）兩個零點，

則f（x）min=f（1）=e+1-a<0，

所以e+1

假設0

要證明x1x2<1，

即證1

又f（x）在（1，+∞）上單調遞增，

即證f（x2）

下面構造函數

F（x）=f（x）-f1x（0

F′（x）=f′（x）+f′1x·1x2

=（x-1）（ex+x-xe1x-1）x2，

由于ex>ex，

所以ex+x>ex+x=（e+1）x，

又函數y=xe1x在（0，1）單調遞減，

所以xe1x>e，

即-xe1x-1<-e-1，

于是ex+x-xe1x-1

所以00，

F（x）在（0，1）單調遞增，

而F（1）=f（1）-f（1）=0，

所以F（x）>0f（x）

22.（1）由C1：x=2+t6，y=t，

消去參數t得y2=6x-2（y≥0）.

（2）C3：2cosθ-sinθ=0，

兩邊乘ρ，得2ρcosθ-ρsinθ=0，

所以C3：y=2x，

聯立y2=6x-2（y≥0），y=2x，

解得x=12，y=1，或x=1，y=2，

C2消去參數s得y2=-6x-2（y≤0），

聯立y2=-6x-2（y≤0），y=2x，

解得x=-1，y=-2，或x=-12，y=-1.

綜上知，C3與C1的交點為12，1和（1，2），C3與C2的交點為（-1，-2）和-12，-1.

23.（1）由柯西不等式知

（a2+b2+4c2）（12+12+12）

≥（a+b+2c）2，

即3×3≥（a+b+2c）2，

且a，b，c是正實數，

故a+b+2c≤3，

當且僅當a=b=2c，即a=b=1，c=12時，等號成立.

（2）由（1）知a+b+2c≤3，且b=2c，

故0

由權方和不等式知

1a+1c=12a+224c≥9a+4c≥3，

故1a+1c≥3.