9.上海卷

一、填空題

1.已知z=1+i（其中i為虛數單位），則2=.

2.雙曲線x29-y2=1的實軸長為.

3.函數f（x）=cos2x-sin2x+1的周期為.

4.已知a∈R，行列式a132的值與行列式a041的值相等，則a=.

5.已知圓柱的高為4，底面積為9π，則圓柱的側面積為.

6.x+y≤0，x-y-1≤0，則z=x+2y的最小值是.

7.二項式（3+x）n的展開式中，x2項的系數是常數項的5倍，則n=.

8.若函數f（x）=a2x-1，x+a，0，x<0，x>0，x=0為奇函數，則參數a的值為.

9.為了檢測學生的身體素質指標，從游泳類1項，球類3項，田徑類4項共8項項目中隨機抽取4項進行檢測，則每一類都被抽到的概率為.

10.已知等差數列{an}的公差不為零，Sn為其前n項和，若S5=0，則Si（i=0，1，2，…，100）中不同的數值有個.

11.若|a|=|b|=|c|=λ，且滿足a·b=0，a·c=2，b·c=1，則λ=.

12.設函數f（x）滿足f（x）=f1x+1，定義域為D=[0，+∞），值域為A，若集合{y|y=f（x），x∈[0，a]}可取得A中所有值，則參數a的取值范圍為.

二、選擇題

13.若集合A=[-1，2），B=Z，則A∩B=（）

（A）{-2，-1，0，1}.（B）{-1，0，1}.

（C）{-1，0}.（D）{-1}.

14.若實數a，b滿足a>b>0，下列不等式中恒成立的是（）

（A）a+b>2ab.（B）a+b<2ab.

（C）a2+2b>2ab.（D）a2+2b<2ab.

圖1

15.如圖1，正方體ABCD|A1B1C1D1中，P、Q、R、S分別為棱AB、BC、BB1、CD的中點，連接A1S，B1D.空間任意兩點M，N，若線段MN上不存在點在線段A1S，B1D上，則稱MN兩點可視，下列選項中與點D1可視的為（）

（A）點P.（B）點B.（C）點R.（D）點Q.

16.已知平面直角坐標系中的點集Q={（x，y）|（x-k）2+（y-k2）2=4|k|，k∈Z}.

①存在直線l與Q沒有公共點，且Q中存在兩點在l兩側;

②存在直線l經過Q中的無數個點，則（）

（A）①成立②成立.

（B）①成立②不成立.

（C）①不成立②成立.

（D）①不成立②不成立.

圖2

三、解答題

17.如圖2，三棱錐的底面為等邊△ABC，O為AC邊中點，PO⊥平面ABC，AP=AC=2.

（1）求三棱錐P|ABC的體積;

（2）若M為BC中點，求PM與平面PAC所成角的大小.

18.已知f（x）=log3（x+a）+log3（6-x）.

（1）若將函數f（x）的圖象向下移m（m>0）個單位，圖象經過點（3，0），（5，0），求實數a，m的值;

（2）若a>-3且a≠0，解關于x的不等式f（x）≤f（6-x）.

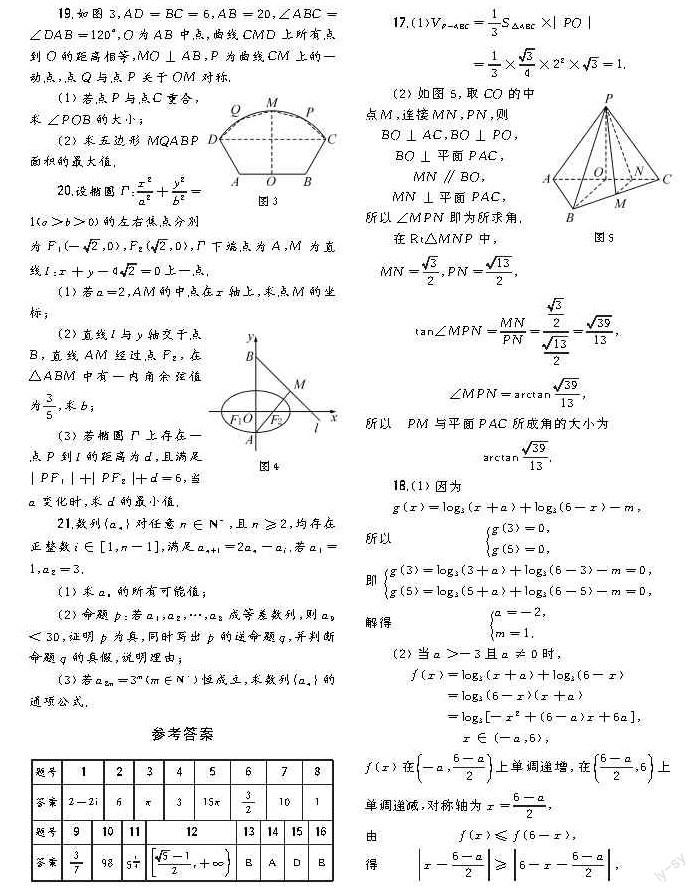
19.如圖3，AD=BC=6，AB=20，∠ABC=∠DAB=120°，O為AB中點，曲線CMD上所有點到O的距離相等，MO⊥AB，P為曲線CM上的一動點，點Q與點P關于OM對稱.

圖3

（1）若點P與點C重合，求∠POB的大小;

（2）求五邊形MQABP面積的最大值.

20.設橢圓Γ：x2a2+y2b2=1（a>b>0）的左右焦點分別為F1（-2，0），F2（2，0），Γ下端點為A，M為直線l：x+y-42=0上一點.

（1）若a=2，AM的中點在x軸上，求點M的坐標;

圖4

（2）直線l與y軸交于點B，直線AM經過點F2，在△ABM中有一內角余弦值為35，求b;

（3）若橢圓Γ上存在一點P到l的距離為d，且滿足|PF1|+|PF2|+d=6，當a變化時，求d的最小值.

21.數列{an}對任意n∈N*，且n≥2，均存在正整數i∈[1，n-1]，滿足an+1=2an-ai.若a1=1，a2=3.

（1）求a4的所有可能值;

（2）命題p：若a1，a2，…，a8成等差數列，則a9<30，證明p為真，同時寫出p的逆命題q，并判斷命題q的真假，說明理由;

（3）若a2m=3m（m∈N*）恒成立，求數列{an}的通項公式.

參考答案

題號12345678答案2-2i6π315π32101題號910111213141516答案37985145-12，+∞BADB

17.（1）VP-ABC=13S△ABC×|PO|

=13×34×22×3=1.

圖5

（2）如圖5，取CO的中點M，連接MN，PN，則

BO⊥AC，BO⊥PO，

BO⊥平面PAC，

MN∥BO，

MN⊥平面PAC，

所以∠MPN即為所求角.

在Rt△MNP中，

MN=32，PN=132，

tan∠MPN=MNPN=32132=3913，

∠MPN=arctan3913，

所以PM與平面PAC所成角的大小為

arctan3913.

18.（1）因為

g（x）=log3（x+a）+log3（6-x）-m，

所以g（3）=0，g（5）=0，

即g（3）=log3（3+a）+log3（6-3）-m=0，g（5）=log3（5+a）+log3（6-5）-m=0，

解得a=-2，m=1.

（2）當a>-3且a≠0時，

f（x）=log3（x+a）+log3（6-x）

=log3（6-x）（x+a）

=log3[-x2+（6-a）x+6a]，

x∈（-a，6），

f（x）在-a，6-a2上單調遞增，在6-a2，6上單調遞減，對稱軸為x=6-a2，

由f（x）≤f（6-x），

得x-6-a2≥6-x-6-a2，

即x-6-a2≥x-6+a2，

所以x-3+a2≥x-3-a2.

當a>0時，得x≥3，

又x∈（-a，6），

所以x∈[3，6）.

當-3

又x∈（-a，6），

所以x∈（-a，3].

19.（1）P在點C的位置時，

OB=10，BC=20，∠ABC=120°.

在△OPB中，

cos∠OBC=OB2+BC2-OC22OB·BC

=-12×102+62-OC22×10×6

=-12，

所以OC=14，

由正弦定理得

OCsin∠OBC=BCsin∠POB，10sin∠POB=14sin120°，

所以sin∠POB=3314，∠POB=arcsin3314.

圖6圖7

（2）連接OQ，OP，曲線CMD上任一點到O的距離相等，則

OQ=OP=OD=OM=14，

所以點Q與點P關于OM對稱，

S△QOM=S△POM，S△AOM=S△BOM.

設∠QOM=∠POM=α，則

∠QOA=∠POB=π2-α，

于是SMQABP=2（S△MQO+S△QOA）

=2×12OM·OQsinα+12OA·OQsinπ2-α

=196sinα+140cosα

=58016sin（α+φ），

tanφ=3564，

所以五邊形MQABP面積的最大值為2874.

20.（1）Γ：x2a2+y2b2=1中，

a=2，b2=a2-c2=2，

所以A（0，-2）.

設M（m，42-m），

AM的中點Gm2，42-2-m2，

由點G在x軸上，

得42-2-m2=0，

即m=32，

所以M（32，2）.

圖8

（2）若cosA=35，

則tanA=43=2b，

所以b=324;

若cosM=35，得

tanA=7，

所以7=2b，

即b=27.

（3）設P（acosθ，bsinθ），

因為|PF1|+|PF2|+d=6，

所以d=6-2a>0，

即a<3.

于是d=|acosθ+bsinθ-42|2

≥|a2+b2-42|2

=|2a2-2-42|2

=4-a2-1，

所以4-a2-1=6-2a，

解得a=53，

即d=6-2a=83，

所以d的最小值為83.

21.（1）n=2，a3=2a2-a1=2×3-1=5;

n=3，a4=2a3-a1=2×5-1=9，

或a4=2a3-a2=2×5-3=7，

a4的所有可能值為7或9.

（2）對于命題p：若a1，a2，a3，…，a8成等差數列，

a1=1，a2=3，

則an=2n-1，a8=15.

對任意n（n≥2），都存在正整數i（1≤i≤n-1）使得

an+1=2an-ai，

a9=2a8-ai≤2a8-ai=29<30，

即a9<30恒成立，

命題p為真命題.

命題p的逆命題q：

若a9<30，則a1，a2，a3，…，a8成等差數列.

結論：q為真命題.

假設：a8≥16，a9=2a8-ai（1≤i≤7），

i=1，a9=2a8-a1≥32-1=31>30，

與a9<30矛盾，

所以a8<16，

a8∈N*，a8≥15.①

若a1，a2，a3，…，ak單調遞增，

ak+1=2ak-ai（1≤i≤k-1）

=ak+（ak-ai）>ak，

a1，a2，a3，…，ak，ak+1單調遞增，

可得a1，a2，a3，…，a8單調遞增，

an+1=2an-ai（1≤i≤k-1）≥2an-an-1，

n=2，a3=2a2-a1=2×3-1=5，

a4≥2a3-a2=7，

a5≥2a4-a3=9，

…，

a8=2a7-a6=15，②

由①②，得a8=15，

同時取等號條件為

a4=7，a5=9，a6=11，a7=13，a8=15，

a1=1，a2=3，a3=5，a4=7，

a5=9，a6=11，a7=13，a8=15，

所以a1，a2，a3，…，a8成等差數列.

綜上知，q為真命題.

（3）a1=1，a2=3，a3=5對任意正整數m，

a2m=3m.

猜想：a2m=3m，a2m+1=5×3m-1（m∈N*）.

證明：由

a2m+1=2a2m-ai，a2m+2=2a2m+1-ai，（1≤i≤2m-1），（1≤i≤2m），

得a2m+2=2（a2m-ai）-aj（1≤i，j≤2m），

3m+1=2（2×3m-ai）-aj，

所以2ai+aj=3m.

利用數學歸納法證明：

a2m+1=5×3m-1（m∈N*）.

①當m=1時，a3=5，命題成立;

②假設m=k，k≥1時，

a2k+1=5×3k-1（k∈N*）.

③則m=k+1時，

2ai+aj=3k+1（1≤i≤2k+1，1≤j≤2k+2）.

當i=j=2k時，2ai+aj=3k+1成立.

若i，j<2k，由（2）證明單調性可知

ai，aj<3k，

即2ai+aj<3k+1與2ai+aj=3k+1矛盾;

若i=2k+1，j<2k，

2ai+aj=2×5×3k-1+aj

=109×3k+1+aj>3k+1，

與2ai+aj=3k+1矛盾;

若i<2k+1，j=2k+2，

2ai+aj=2ai+3k+1，

與2ai+aj=3k+1矛盾;

若i<2k+1，j=2k+1，

2ai+aj<2×5×3k-2+5×3k-1

=2527×3k+1<3k+1，

與2ai+aj=3k+1矛盾.

綜上知，i=j=2k，即m=k+1時，

a2k+1=2a2k+2-a2k=2×3k+1-3k

=5×3k（k∈N*）成立，

a1=1，a2m=3m，

a2m+1=5×3m-1（m∈N*），

a3=5.