7.浙江卷

一、選擇題

1.設集合A={1，2}，B={2，4，6}，則A∪B=（）

（A）{2}.（B）{1，2}.

（C）{2，4，6}.（D）{1，2，4，6}.

2.已知a，b∈R，a+3i=（b+i）i（i為虛數單位），則（）

（A）a=1，b=-3.（B）a=-1，b=3.

（C）a=-1，b=-3.（D）a=1，b=3.

3.若實數x，y滿足約束條件x-2≥0，2x+y-7≤0，x-y-2≤0，

則z=3x+4y的最大值是（）

（A）20.（B）18.（C）13.（D）6.

4.設x∈R，則“sinx=1”是“cosx=0”的（）

（A）充分不必要條件.

（B）必要不充分條件.

（C）充分必要條件.

（D）既不充分也不必要條件.

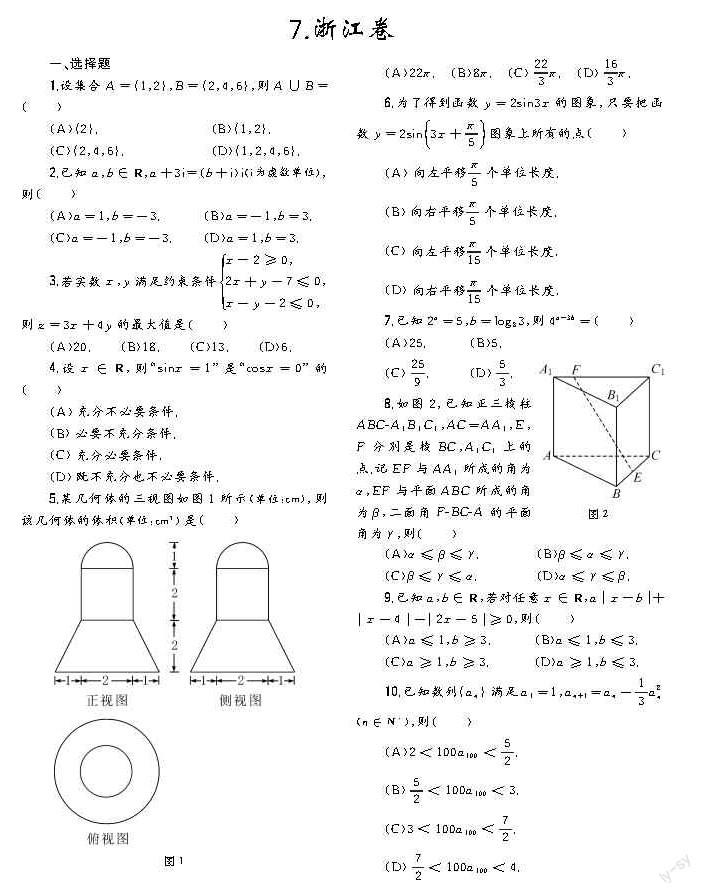
5.某幾何體的三視圖如圖1所示（單位：cm），則該幾何體的體積（單位：cm3）是（）

圖1

（A）22π.（B）8π.（C）223π.（D）163π.

6.為了得到函數y=2sin3x的圖象，只要把函數y=2sin3x+π5圖象上所有的點（）

（A）向左平移π5個單位長度.

（B）向右平移π5個單位長度.

（C）向左平移π15個單位長度.

（D）向右平移π15個單位長度.

7.已知2a=5，b=log83，則4a-3b=（）

圖2

（A）25.（B）5.

（C）259.（D）53.

8.如圖2，已知正三棱柱ABC|A1B1C1，AC=AA1，E，F分別是棱BC，A1C1上的點.記EF與AA1所成的角為α，EF與平面ABC所成的角為β，二面角F|BC|A的平面角為γ，則（）

（A）α≤β≤γ.（B）β≤α≤γ.

（C）β≤γ≤α.（D）α≤γ≤β.

9.已知a，b∈R，若對任意x∈R，a|x-b|+|x-4|-|2x-5|≥0，則（）

（A）a≤1，b≥3.（B）a≤1，b≤3.

（C）a≥1，b≥3.（D）a≥1，b≤3.

10.已知數列{an}滿足a1=1，an+1=an-13a2n（n∈N*），則（）

（A）2<100a100<52.

（B）52<100a100<3.

（C）3<100a100<72.

（D）72<100a100<4.

二、填空題

11.我國南宋著名數學家秦九韶，發現了從三角形三邊求面積的公式，他把這種方法稱為“三斜求積”，它填補了我國傳統數學的一個空白.如果把這個方法寫成公式，就是S=14c2a2-c2+a2-b222，其中a，b，c是三角形的三邊，S是三角形的面積.設某三角形的三邊a=2，b=3，c=2，則該三角形的面積S=.

12.已知多項式（x+2）（x-1）4=a0+a1x+a2x2+a3x3+a4x4+a5x5，則a2=，a1+a2+a3+a4+a5=.

13.若3sinα-sinβ=10，α+β=π2，則sinα=，cos2β=.

14.已知函數f（x）=-x2+2，x≤1，x+1x-1，x>1，則ff12=;若當x∈[a，b]時，1≤f（x）≤3，則b-a的最大值是.

15.現有7張卡片，分別寫上數學1，2，2，3，4，5，6.從這7張卡片中隨機抽取3張，記所抽取卡片上數字的最小值為ξ，則P（ξ=2）=，E（ξ）=.

16.已知雙曲線x2a2-y2b2=1（a>0，b>0）的左焦點為F，過F且斜率為b4a的直線交雙曲線于點A（x1，y1），交雙曲線的漸近線于點B（x2，y2），且x1<0

17.設點P在單位圓的內接正八邊形A1A2…A8的邊A1A2上，則PA12+PA22+…+PA82的取值范圍是.

三、解答題

18.在△ABC中，角A，B，C所對的邊分別為a，b，c.已知4a=5c，cosC=35.

（1）求sinA的值;

（2）若b=11，求△ABC的面積.

19.如圖3，已知ABCD和CDEF都是直角梯形，AB∥DC∥EF，AB=5，DC=3，EF=1，∠BAD=∠CDE=60°，二面角F|DC|B的平面角為60°.設M，N分別為AE，BC的中點.

圖3

（1）證明：FN⊥AD;

（2）求直線BM與平面ADE所成角的正弦值.

20.已知等差數列{an}的首項a1=-1，公差d>1.記{an}的前n項和為Sn（n∈N*）.

（1）若S4-2a2a3+6=0，求Sn;

（2）若對于每個n∈N*，存在實數cn，使得an+cn，an+1+4cn，an+2+15cn成等比數列，求d的取值范圍.

21.如圖4，已知橢圓x212+y2=1.設A，B是橢圓上異于P（0，1）的兩點，且點Q0，12在線段AB上，直線PA，PB分別交直線y=-12x+3于C，D兩點.

圖4

（1）求點P到橢圓上點的距離的最大值;

（2）求|CD|的最小值.

22.設函數f（x）=e2x+lnx（x>0）.

（1）求f（x）的單調區間;

（2）已知a，b∈R，曲線y=f（x）上不同的三點（x1，f（x1）），（x2，f（x2）），（x3，f（x3））處的切線都經過點（a，b），證明：

（i）若a>e，則0

（ii）若0

參考答案

題號12345678910答案DBBACDCADB題號11121314答案2348;-231010;453728;3+3題號151617答案1635;127364[12+22，16]

18.（1）由于cosC=35，sinC>0，

則sinC=45.

由正弦定理知4sinA=5sinC，

則sinA=55.

（2）由sinC=45>sinA=55，

則A

故b=acosC+ccosA=35a+255c=115a=11，

所以a=5，

△ABC的面積S=12absinC=22.

19.（1）因為CD⊥CB，CD⊥CF，

所以∠FCB=60°，CD⊥平面CBF，

于是CD⊥FN.

又CF=3（CD-EF）=23，

CB=3（AB-CD）=23，

所以△BCF是等邊三角形，

圖5

即CB⊥FN，

于是FN⊥平面ABCD，

故FN⊥AD.

（2）由于FN⊥平面ABCD，故可如圖5建立坐標系，

于是B（0，3，0），

A（5，3，0），F（0，0，3），

E（1，0，3），D（3，-3，0），

則M3，32，32，BM=3，-32，32，

DA=（2，23，0），DE=（-2，3，3），

平面ADE的法向量n=（3，-1，3）.

設BM與平面ADE所成角為θ，

則sinθ=|BM·n||BM|·|n|=5714.

20.（1）設an=（n-1）d-1，

依題意得6d-4-2（d-1）（2d-1）+6=0，

解得d=3，

則an=3n-4，n∈N*，

于是Sn=3（1+2+…+n）-4n

=3n（n+1）-8n2

=n（3n-5）2，n∈N*.

（2）設an=（n-1）d-1，則

[cn+（n-1）d-1][15cn+（n+1）d-1]

=（4cn++nd-1）2，

15c2n+[（16n-14）d-16]cn+（n2-1）d2-2nd+1

=16c2n+8（nd-1）cn+n2d2-2nd+1，

c2n+[（14-8n）d+8]cn+d2=0，

故Δ=[（14-8n）d+8]2-4d2

=[（12-8n）d+8][（16-8n）d+8]

≥0，

[（3-2n）d+2][（2-n）d+1]≥0，

對任意正整數n成立.

n=1時，顯然成立;

n=2時，-d+2≥0，則d≤2;

n≥3時，[（2n-3）d-2][（n-2）d-1]

>（2n-5）（n-3）≥0.

綜上知，1

21.（1）設Q（23cosθ，sinθ）是橢圓上一點，

P（0，1），

則|PQ|2=12cos2θ+（1-sinθ）2

=13-11sin2θ-2sinθ

=14411-11sinθ+1112

≤14411，

故|PQ|的最大值是121111.

（2）設直線AB：y=kx+12，

直線與橢圓聯立，得

k2+112x2+kx-34=0.

設A（x1，y1），B（x2，y2），

故x1+x2=-kk2+112，x1x2=-34k2+112，

PA：y=y1-1x1x+1與y=-12x+3交于點C，

則xC=4x1x1+2y1-2=4x1（2k+1）x1-1.

同理xD=4x2x2+2y2-2=4x2（2k+1）x2-1，

則|CD|=1+14·|xC-xD|

=524x1（2k+1）x1-1-4x2（2k+1）x2-1

=25x1-x2[（2k+1）x1-1][（2k+1）x2-1]

=25x1-x2（2k+1）2x1x2-（2k+1）（x1+x2）+1

=25kk2+1122+3k2+112-（2k+1）234k2+112+（2k+1）kk2+112+1

=352·16k2+13k+1

=655·16k2+1·916+13k+1

≥655，

當且僅當k=316時取等號.

22.（1）f′（x）=1x-e2x2=2x-e2x2，

故f（x）在0，e2上單調遞減，在e2，+∞上單調遞增.圖6

（2）（i）不妨設

x1

則x1，x2，x3滿足

y=f′（xi）（x-xi）+f（xi），

所以x1，x2，x3是f′（x）（x-a）-f（x）+b=0的三個正實數根，

即1x-2ex2（x-a）-e2x-lnx+b=0.

記g（x）=1x-2ex2（x-a）-e2x-lnx+b

=0，a>e，

g′（x）

=1x-e2x2+-1x2+ex3（x-a）+e2x2-1x

=-1x3（x-e）（x-a），

則g（x）在（0，e）上單調遞減，（e，a）上單調遞增，（a，+∞）上單調遞減，

由于x1，x2，x3是f′（x）（x-a）-f（x）+b=0的三個正實數根，

則0a.

又由于x→0時，

g（x）→-lnx→+∞，g（x）=b-a2e-1，

g（a）=-e2a-lna+b;

x→+∞時，g（x）→-lnx→-∞，

于是g（e）=b-a2e-1<0，

g（a）=-e2a-lna+b=b-f（a）>0，

由于b

要證b

只需證a2e+1

即e2a+lna>32，

由（1）知a>e時，f（a）>f（e）=32.

綜上知，0

（ii）由于

g′（x）=-1x3（x-e）（x-a），0

則g（x）在（0，a）上單調遞減，（a，e）上單調遞增，（e，+∞）上單調遞減，

圖7

則0

ae.

又由于x→0時，

g（x）→-lnx→+∞，

g（e）=b-a2e-1，

g（a）=-e2a-lna+b，

x→+∞時，g（x）→-lnx→-∞，

于是g（e）=b-a2e-1>0，

g（a）=-e2a-lna+b<0，

故a2e+1

由于 g（x）=1x-e2x2（x-a）-e2x-lnx+b

=1-a+ex+ea2x2-lnx+b.

記x=et，ae=m∈（0，1），

則-a+eet+a2et2+lnt+b

=lnt+m2t2-（m+1）t+b=0，

要證2e+e-a6e2<1x1+1x3<2a-e-a6e2.

記t1=ex1，t3=ex3，

k=t1t3=x3x1>ea=1m>1，

只需證13-m6=2+e-a6e

<2ea-e-a6e=2m-1-m6，

即證t1+t3-13-m6t1+t3-2m+1-m6

<0，

即t1+t3-2-2m<（m-13）（m2-m+12）36m（t1+t3），

由lnt1+m2t23-（m+1）t1

=lnt3+m2t23-（m+1）t3，t1>t3，

故lnt1-lnt3+m2（t21-t23）-（m+1）（t1-t3）=0，

得t1+t3-2-2m=-2m·lnt1-lnt3t1-t3，

只需證-2m·lnt1-lnt3t1-t3

<（m-13）（m2-m+12）36m（t1+t3），

即證t1+t3t1-t3lnt1t3+（m-13）（m2-m+12）72（t1+t3）>0，

由于t1=kt3，

即證 （k+1）lnkk-1+（m-13）（m2-m+12）72>0.

記φ（x）=（x+1）lnxx-1（x>1），

φ′（x）=1（x-1）2x-1x-2lnx>0，

則φ（x）在（1，+∞）上單調遞增，

于是（k+1）lnkk-1+（m-13）（m2-m+12）72

>m+1m-1lnm+（m-13）（m2-m+12）72.

記

w（x）=lnx+（x-1）（x-13）（x2-x+12）72（x+1）

（0

只需證w（x）>0，

由w′（x）=（x-1）272x（x+1）2（3x3-20x2-49x+72）

>（x-1）272x（x+1）2（3x3+3）>0，

知w（x）在（0，1）上單調遞減，

故w（x）>w（1）=0，得證.