強化解后反思 驅動深度學習

福建省石獅市石光中學 (362700) 許麗拉

解后反思指的是學生在問題解決之后，對解題思路、解題過程、解題結果、解題實質進行自我監控、自我評價和我調節的過程.《普通高中數學課程標準(2017年版)》中11次提到反思，如“做題是解決問題的過程，包括描述問題、教學表達、建立模型、求解模型、得到結論、反思完善等”[1]；“體現數學學科核心素養的四個方面有情境與問題、知識與技能、思維與表達、交流與反思”[1]等等.數學教育家波利亞曾說過：通過回顧所完成的解決問題的過程，通過思考與檢驗結果，回顧解題思路，能鞏固學生的知識，提升學習能力.

深度學習是指學生在教師地引領下，深度參與數學學習活動，并將原有的知識遷移到新的情境中解決問題的學習[2].深度學習關注學生的深度理解、反思、體驗及問題解決與遷移運用，重在引導學生通過深切的體驗與深入的反思，達成對數學本質和知識意義的滲透理解[2].教學實踐表明，培養學生解后反思的習慣，有助于學生辯析、厘清、歸納與之相關的問題，促使他們全方位、多角度地對問題及思維過程進行再驗證、再認識,培養元認知能力，使其對問題的認識從感性逐步上升到理性，實現深度學習.

1 反思解題結果，在“再認知”中提升自我監控能力

在數學教學中，經常發現這樣的現象：對于錯題，教師雖反復講評，卻收效甚微，其主要原因是這種灌輸式的、平鋪直敘的講評使得有錯誤的學生沒有真正領悟問題的實質，無法將課本內容內化為自己的理解[3].事實上，糾正學生的錯誤不能只依賴教師正面的示范與重復的訓練，而是學生“自我否定”的一個過程，即應該引導學生自我反思，在反思體驗中真正弄清錯誤原因，自我糾錯.因此教師應精選典型問題，引導學生解后反思，克服思維的盲目性，提升批判性思維能力.

案例1 已知ab<0,a+b=1,二項式(a+b)9展開式按a的降冪排列，第三項不小于第二項，則a的取值范圍是.

很多學生的解題過程如下：

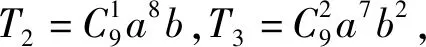
同學們非常驚訝：“結果和題設ab<0矛盾，為什么會這樣？”教師覺得這時正是培養學生反思意識的契機，因此引導學生進行反思：

反思1：問題給出的條件ab<0,a+b=1,得到充分利用了嗎？

反思2：由ab<0,a+b=1能得到a的一個取值范圍嗎？此范圍和以上解題結果相同嗎？

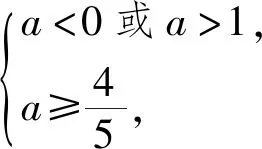
不經過解后反思，是難以察覺這個錯誤的.在教學中，教師應該把學生認識上的偏差當作反面教材，引導其反思，這樣有利于培養學生思維的批判性與嚴謹性，提升學生自我評價與自我監控能力，從而達成對自我數學認知的再認知，促進深度學習.

2 反思解題思路，在導問中孕育“生成”

一個問題往往因思考的角度不同具有多種解決思路，因此解決了一個問題后不應該就此止步不前，要引領學生反思.反思不是簡單的檢驗，而是引領學生依據問題的結構特征，從解題方法、解題思路等進行全方位、多角度的思考：你是如何思考的？選擇哪一條途徑？為何這樣思考？解題的關鍵在哪一步？該題是否還有其它解法？這些方法哪一種最簡便？哪一種最巧妙？哪一種最典型？解題過程滲透了哪幾種數學思想方法？問題是否可以變式、拓展、引申？堅持這樣的反思，能促進學生深度思維，拓寬解題思路，并積累具有規律性的解題經驗，促進課堂有效生成.

案例2 “三角函數復習課”教學片斷

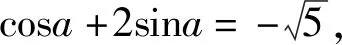
經過探究，學生發現了本題的多種方法，教師展示各種解法.

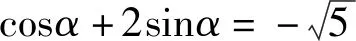
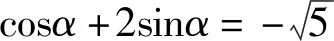
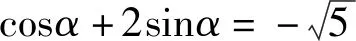
為了提高問題的教育價值，教師沒有急于進入下一題，而是提出以下問題，讓學生反思.

反思1：請大家比較以上幾種方法，并提煉出解題過程中所滲透的數學思想.

生1：思路1利用構造法,通過構造方程，聯立方程組求解，思路自然，但運算量較大；思路2運用“1”的代換轉化成齊次分式得到tana的值，蘊涵著方程思想；思路3借助三角函數輔助角公式，把未知化歸成已知.

反思2：該題是否還有其它的方法？能否另辟蹊徑？

生2：可以運用柯西不等式(cosα+2sinα)2≤(sin2α+cos2α)(12+22)=5，等號當且僅當2cosα=sinα時成立，恰好滿足題設，故tana=2.

師：很好！利用柯西不等式，并運用了等號成立時的情況.

反思3：數形結合是我們解題給出中經常采用的思想方法，該題可以利用數形結合思想解決嗎？

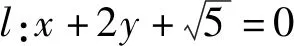
師：太棒了!生3利用數形結合思想把問題化歸成直線和圓的位置關系問題求解,非常簡便，滲透了轉化與化歸思想.

教師引導學生站在新的高度去審視問題，從不同視角探詢解題思路，在多種思想與方法的碰撞中，學生對數學的認識從感性上升到理性，思維的靈活性與深刻性獲得發展，提升了直觀想象、邏輯推理素養，達到了深度學習.

3 反思解題實質，在“頓悟”中實現思維進階

數學家波利亞曾說過：“數學問題的解決僅僅只是一半，而更重要的是解題之后的回顧與反思.”解完一道題后，教師應引導學生反思，它是對問題的“再認知”，是解題的進一步深化，有利于“織題成網，串題成鏈”，使零散的數學知識串成有機整體.這樣學生所收獲的不僅僅是一道題目的解法，而是一類問題的解決方法，有助于發展與完善學生的數學思維，形成有效的“思維鏈”.

案例3 “圓錐曲線復習課”教學片斷

完成了本題后，教師引導學生反思.

反思1：若把問題中的距離的比變成1，則點M的軌跡是什么？

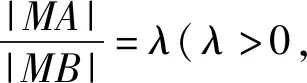
教師引導學生探究得：當λ>0且λ≠1時，點M的軌跡是個圓.

師：此結論是數學家阿波羅尼斯發現的，故該圓叫做“阿波羅尼斯圓”，它的應用非常廣泛.

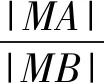
反思4：設A、B是平面內兩定點，如果動點M滿足|MA|·|MB|為定值，那么點M的軌跡是什么？

反思5：設A、B是平面內兩定點，如果動點M滿足|MA|2+|MB|2為定值，那么點M的軌跡是什么？

反思6：設A、B是平面內兩定點，如果動點P滿足||MA|2-|MB|2|為定值，則點M的軌跡是什么？

反思7：平面內到三個定點的距離的和是定值的點的軌跡是什么？

案例3從教材習題出發，引導學生進行反思，挖掘其教學功能.通過循序漸進、逐步深入的反思，讓學生有效地體悟、內化相關知識，使學習活動產生“連鎖反應”，形成有序化、條理化的一個有機體系.在問題解決中，學生積累了用代數方法研究解析幾何問題的經驗，實現了從有效教學到深度學習的過渡，助推數學抽象素養、邏輯推理素養的發展.

4 結語

總之，解后反思對驅動學生深度思考、提升學生核心素養乃至教師的專業發展都有著重要作用，但學生反思習慣的形成決非朝夕之功，需要循序漸進、日積月累、螺旋上升.因此在數學教學中，教師應不失時機地對學生進行反思意識、反思方法的滲透，使反思內化為學生的一種自覺學習行為；解決問題之后，應留給學生反思的時間，引導學生通過反思解題思路、解題結果、解題實質，不斷剖析自我，克服錯誤現象，提煉解題經驗，追求解法優化，提高學習能力.這樣的反思，有助于激發學生的學習興趣，完善認知結構、形成學習策略，促進學生從淺層學習走向深度學習.因此數學教學應當擯棄“他律”狀態下的機械灌輸，凸顯“自律”意義上的生命體征，為學生的深度學習搭好“腳手架”，使他們在對問題的“再認知”中積累基本活動經驗，領悟數學思想方法，從“不識廬山真面目，只緣身在此山中”走向“會當臨絕頂，一覽眾山小”的境界，讓數學核心素養落地生根.