定比點差法的應用
——圓錐曲線中線段定比分點問題的探究

云南省下關第一中學 (671000) 郭潤仙

處理直線與圓錐曲線的交匯問題，我們經常采用的方法就是：先聯立直線和圓錐曲線的方程，再靈活利用根與系數的關系加以求解，即利用了“設而不求”的方法.但實際上，如果能避開一元二次方程的判別式以及根與系數的關系，即利用“設而求”的方法，或許更為簡單.現就圓錐曲線中有關線段定比分點問題進行探究，給出一種更好的解題方法，即“定比點差法”.

類型一、處理弦長被坐標軸分成兩段的相關問題

(1)求橢圓C的標準方程；

圖1

綜上，所求m的取值范圍是(-2,-1)∪(1,2)∪{0}．

評注：本題第二問利用定比點差法解題時，必須根據m與0的關系進行討論；否則，極易產生漏解.

類型二、處理相關定直線與定點問題

評注：兩個調和定比分點式子一齊上場才能解決問題，這是定比點差法的核心.

(1)求橢圓C的方程；

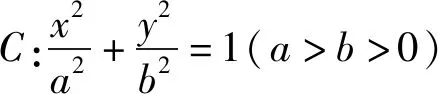
(1)求橢圓C的離心率；

(2)直線λx+μy=1是否經過定點？若經過，求出定點坐標；若不經過，請說明理由.

評注：本題第二問求解的關鍵在于將“定比點差法”靈活運用兩次，均得到點P橫坐標的含參表達式，進而獲得兩個參數λ,μ滿足的等式，便于進一步分析含參直線λx+μy=1是否經過定點.

類型三、處理坐標軸為角平分線類試題

圖2

(1)當l與x軸垂直時，求直線AM的方程；

(2)設O為坐標原點，證明：∠OMA=∠OMB.

(2)當直線l與x軸重合時，因為∠OMA=0°,∠OMB=0°，所以∠OMA=∠OMB.

當直線l與x軸垂直時，因為OM為線段AB的垂直平分線，所以∠OMA=∠OMB.

當直線l與x軸不重合也不垂直時，如圖3所示，作點B關于x軸的對稱點B′，連接AB′，并延長AB′與x軸交于點N，連接BN.下面通過證明N與M重合，來證明∠OMA=∠OMB.

圖3

綜上，必有∠OMA=∠OMB.

類型四、處理相交弦中的定點定值問題

注意：在圓錐曲線問題中，當兩條弦所在直線的公共點在坐標軸上時，運用常規解法非常繁瑣，若將坐標變換成比值，則往往會事半功倍.

(1)求橢圓M的方程；

(2)若k=1，求|AB|的最大值；

評注：上述求解關鍵是先兩次活用“定比點差法”可得⑦式，再將三點共線轉化為直線的斜率相等可得⑧式.顯然，第三問涉及字母形式的化簡、運算量較大，需要特別認真、細心一些.

總之，結合上述歸類解析可知，靈活運用“定比點差法”可迅速分析、解決圓錐曲線中有關涉及線段定比分點問題，其優點是技巧性的規律較強，有利于減少化簡、運算量，從而提高解題的速度與準確性.