導數視角下雙變量問題的多角度處理方法

浙江省杭州學軍中學海創園校區 (311121) 陶勇勝

在近些年高考壓軸題中，以導數為背景的雙變量問題一直是導數題中的熱點和難點[1].這一類問題因含兩個變量，其解法眾多且技巧性強，常以壓軸題形式出現，對學生的數學抽象、邏輯推理、數學建模等核心素養有較高的要求.本文從一道2021年全國高考題說起，對導數視角下雙變量問題進行多角度探究，以期優化解決此類問題的思維策略.

一、構造函數角度

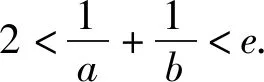
證明：(1)f(x)在(0，1)上單調遞增，在(1，+∞)上單調遞減，過程略.

下面證明：2

證法1：(利用對稱，構造函數)令F(x)=f(1+x)-f(1-x)，其中00，所以F(x)在(0，1)上單調遞增，因此F(x)>F(0)=0，從而f(1+x)>f(1-x).令x=1-x1，代入不等式f(1+x)>f(1-x)中，得到f(2-x1)>f(x1)，即f(2-x1)>f(x2)，又因為f(x)在(1，+∞)上單調遞減且x2>1，2-x1>1，所以x2>2-x1，即x1+x2>2.

評注：證明不等式x1+x22的過程有較大不同，原因是函數g(x)=x2-2xlnx在(0，+∞)上有單調性，而函數h(x)=x2-exlnx在(0，+∞)上不是單調函數，因此，利用函數的單調性無法直接證明h(x2)f(x)，當1

二、數形結合角度

“數少形時少直覺，形少數時難入微”，數形結合是解決函數及導數問題的重要思想方法，下面從數形結合角度談談處理雙變量不等式問題.

1.以直代曲

圖1

圖2

評注：2015年天津理科卷第15題用雙切線代替曲線[1]及2021年全國新高考Ⅰ卷第22題(例1)用切線、割線代替曲線[5]證明雙變量不等式，說明以直代曲的方法是處理雙變量問題的有效方法之一.

2.以曲代曲

這是一道雙變量不等式證明的經典題，可以通過齊次化、比值代換、比差代換、增量法[2]-[5]等方法求解，下面從數形結合角度，以曲代曲的方法進行探究：

圖3

圖4

三、不等式放縮角度

例5 題目同例1.

(Ⅰ)不等式x1+x2>2的證明.

(Ⅱ)不等式x1+x2

證法2：因為00，得到f(x1)=x1-x1lnx1>x1.所以x1+x20，所以G(x)在(1，e)上單調遞增，從而G(x)

分析：(1)略；(2)本題是以導數為背景的雙變量不等式問題，涉及函數、不等式和導數等眾多知識，看似變量較多，實質是極值點偏移問題.欲證不等式2(x2-x1)>x5-x3，采用分析法，將目標進行等價變形，即要證明2x2-2x1>(x5+x4)-(x3+x4)，只要證明x3+x4>2x1，x4+x5<2x2即可.

四、主元角度

數學解題中，有些題目按常規解法較難，若更換觀察角度，一動一靜，主客換位思考，往往有“出奇制勝”的效果.

五、結束語

雙變量不等式的證明是考查導數部分內容的一個重要抓手，導數與不等式等知識綜合對學生的思維能力有很高的要求，深刻考查學生的綜合能力和核心素養，通常以壓軸題出現，因此，導數及其應用的處理應重視直觀，數形結合，突出本質，關注過程，歸納通性通法，這就要求教師精選例題、習題，通過對典型例題進行多角度探究和適當變式，讓學生深刻領悟問題的本質，掌握解決問題的一般方法和規律，體會其中蘊含的數學思想.