多點開花 妙解三角形

福建省福清第一中學 (350300) 葉誠理 林品玲

在高三一輪復習后，學生對高中數學知識體系有了較為全面的認識，對數學思想方法有了一定程度的掌握，在解題過程中往往會從不同的角度考慮一個問題，產生了各種不同的解法，也許學生的過程與方法未必與標準答案一致，但其中不乏簡潔、漂亮的解法，值得我們老師關注．以下是筆者在高三復習教學中遇到的一道解三角形的題目.

問題如圖1，△ABC中，AC=2，AB=1，AD=k，點D為BC邊上的動點，BD：DC=1:2，試求k的取值范圍．

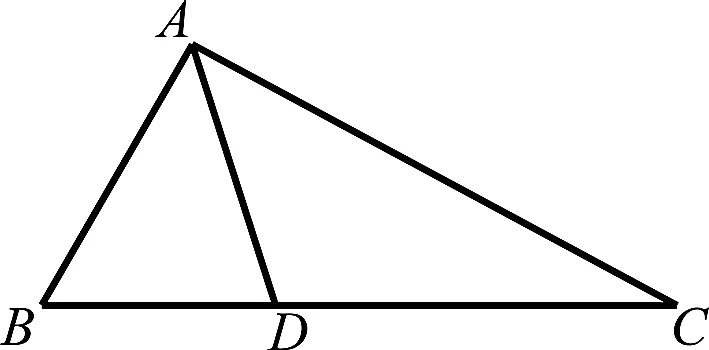
圖1

本題考查學生運用余弦定理、誘導公式解三角形，求邊的關系用到函數思想，化解三角函數關系式則考查了運算求解能力，試題難度較小，學生容易上手．

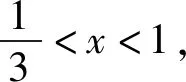
評注：該解法從點D分BC的比例入手，根據余弦定理，利用兩角互補，算出AD的函數表達式，思路直接，易錯點是忽略了三角形邊的關系而求錯定義域．

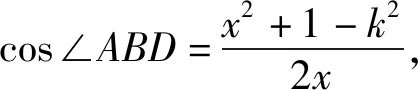
評注：該解法把同一個角B放在兩個不同的三角形中，利用數學中對同一變量“算兩次”的思想構建AD的函數表達式，與解法一可謂異曲同工．

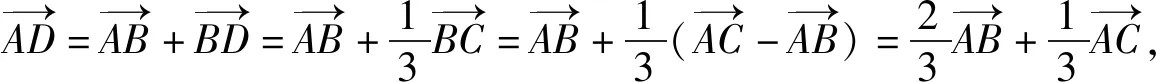
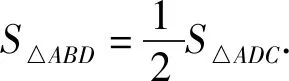
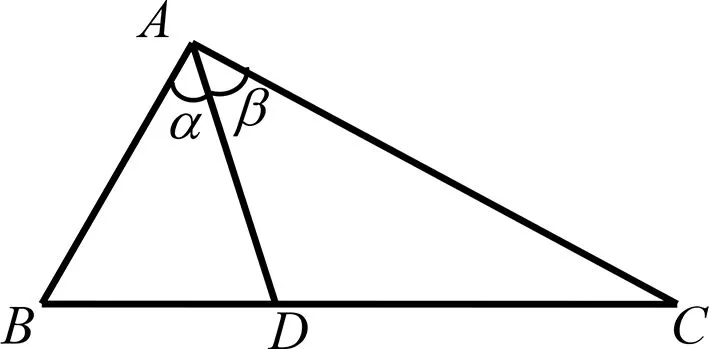
圖2

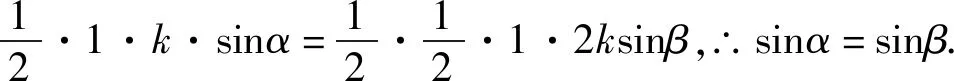
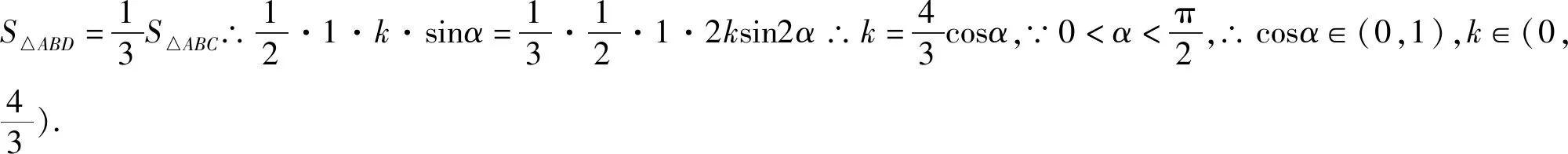
評注：該解法從等高的兩三角形面積關系入手，證明AD為∠BAC的角平分線，揭示了問題的本質，打開解題思路，再次利用面積公式和三角恒等變換公式構建AD的三角表達式，十分巧妙．

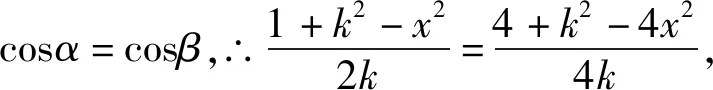
評注：在證明直線AD為∠BAC的角平分線后，直接利用余弦定理解題，與解法一、解法二不謀而合．

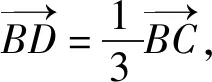
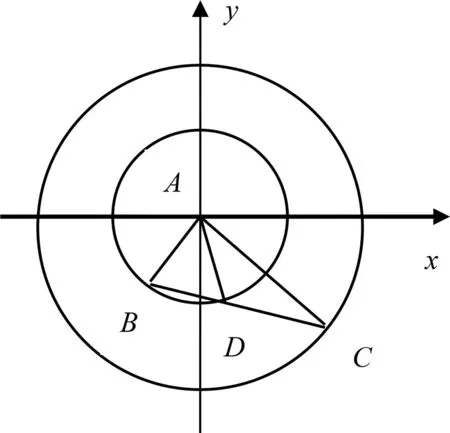
圖3

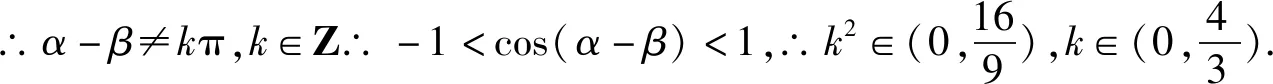
評注：該解法的亮點在于在原三角形圖上建立平面直角坐標系，根據線段長度，巧設點的坐標，進而通過兩點距離公式，再結合三角函數的性質得出線段AD的取值范圍，體現了解析幾何的特點：用代數的方法來研究幾何問題．

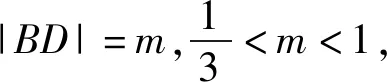
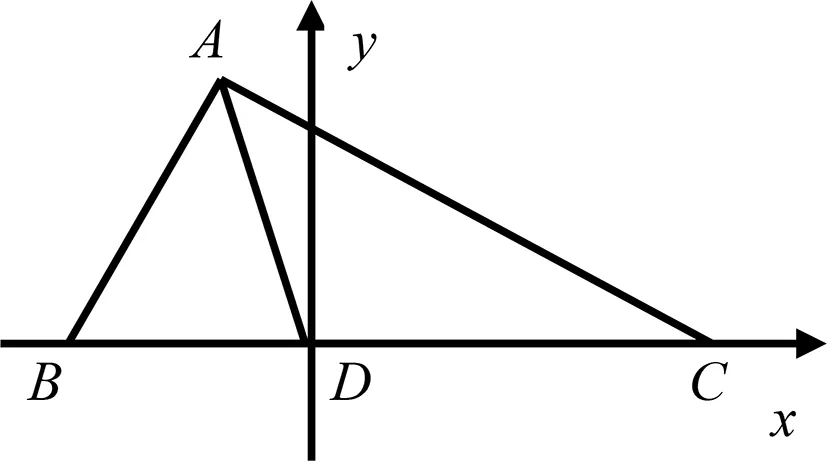
圖4

評注：該解法也是通過建立直角坐標系來實現點的坐標表示，通過以點D為原點，突出了點A的幾何特征：可看成以點B、C為圓心，1和2為半徑的兩個圓的交點，故可聯立這兩個圓的方程，算出交點軌跡，轉化為求這個交點到原點的距離，其思路也十分巧妙．

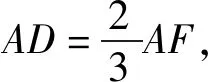
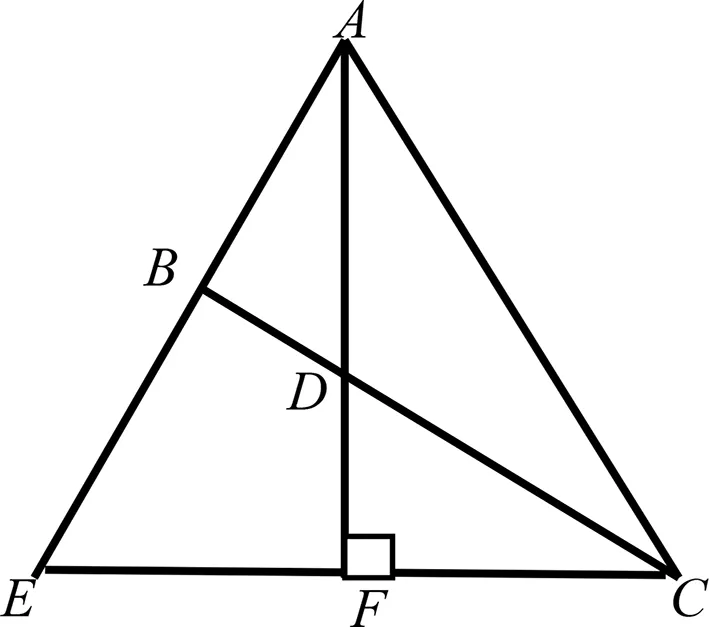
圖5

評注：該解法充分利用已知三角形兩鄰邊比為1:2，添加輔助線，構造等腰三角形，進而得出點D為新得的三角形的重心，再利用重心性質解題，該解法的精妙之處在于構造的輔助線使得問題的求解豁然開朗．

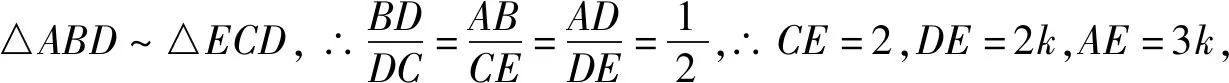
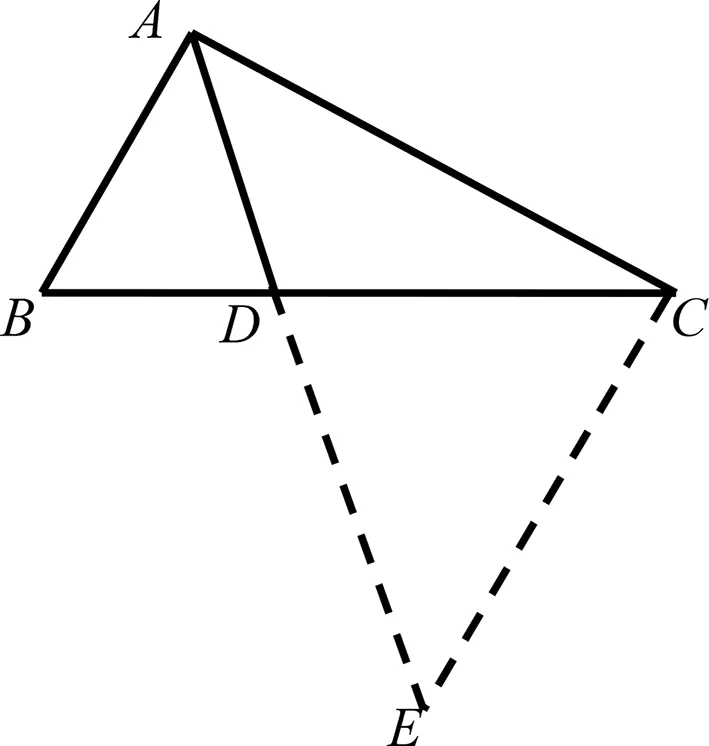
圖6

評注：該解法通過構造相似三角形，利用相似比把所求問題集中到一個三角形中，直接利用三邊關系建立不等關系，其思路返璞歸真，計算量小．

解法十：(關注角變化，運用極限思想)角B的變化范圍是大于0且小于π，由解法6的圖3，固定AB邊，當角B從0變大到π時，AD也跟著連續變大，下面用極限法考慮：

(1)當角B→0時，如圖7，BC邊上的高趨近0，此時AD→0;

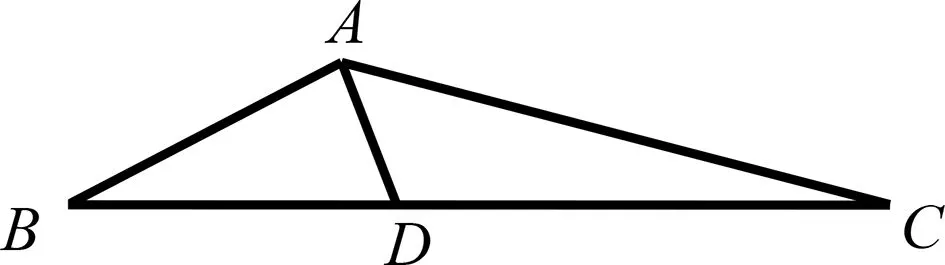
圖7

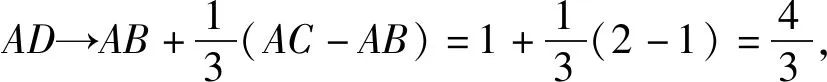
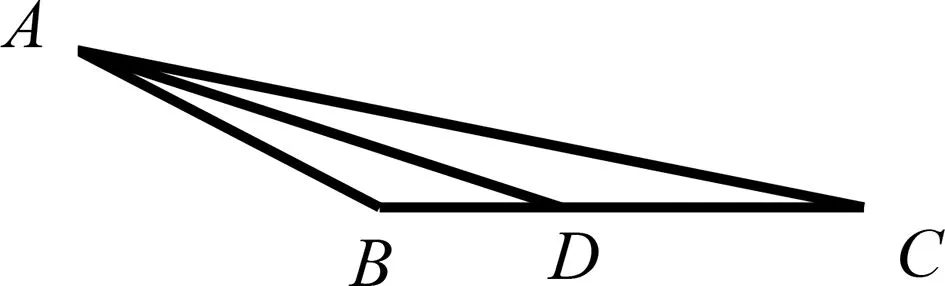
圖8

評注：該解法從點B的變化趨勢入手，單刀直入，從運動變化的觀點，利用極限思想立竿見影地算出線段AD的取值范圍，其思路簡潔明了，令人拍案叫絕，美中不足在于其論證不夠嚴密．

以上解法讓學生感受到數學思維的無限魅力．解題中用到的知識涉及函數、方程、不等式、三角函數、平面向量、平面幾何、解析幾何等；集中考查了學生的抽象概括能力，運算求解能力和創新應用意識；用到的數學思想有函數與方程思想、化歸與轉化思想、數形結合思想、分類與整合思想，極限思想等．本題的一題多解，彰顯學生靈活合理地運用所學知識解決實際問題的能力，是一道值得我們欣賞和品味的好題．