運用“數形結合”提高學習效度
佘芳芳
運用“數形結合”提高學習效度
佘芳芳
(莆田市城廂區霞林學校,福建莆田351100)
在數學學習過程中利用“數形結合”的思想研究數學問題,把晦澀的數量關系用簡單明了的幾何圖形來展現,又或是將圖形的幾何屬性通過嚴密精準的數量關系闡明出來,都能夠讓概念理解走向深刻,直觀可見地理解算理,更加凸顯數學本質,解決問題形象化、多樣化,從而提高問題解決的邏輯思考和推理判斷水平,提升數學學習效度。
數形結合;數學思想;學習效度
“數形結合”是一種重要的數學思想,在輔助學生探究解題方法中充分發揮了其優勢,已經成為了引導學生分析數學問題的重要手段之一。在探索數學問題的解答方法時,學生可以依靠“數形結合”思想的獨特特點,把晦澀的數量關系用簡單明了的幾何圖形展現,又或通過數字的精確性特點表示形的幾何屬性,能夠讓概念理解走向深刻,直觀可見地理解算理算法,更加凸顯數學本質,解決問題形象化,從而提高問題解決的邏輯思考和推理判斷水平,幫助學生提升數學學習效度。
一、以形助數,讓概念理解走向深刻
正確理解數學概念是數學學習的前提與基礎,概念的抽象性又往往成為學生正確理解概念的一道檻。因此,概念教學中,教師如果能夠在學生經歷知識產生的過程,以形助數,借助圖形表征概念的基本特征,使抽象的數學概念直觀化、形象化,那么,學生就容易實現對概念本質特征的深刻理解,深度建構概念模型。
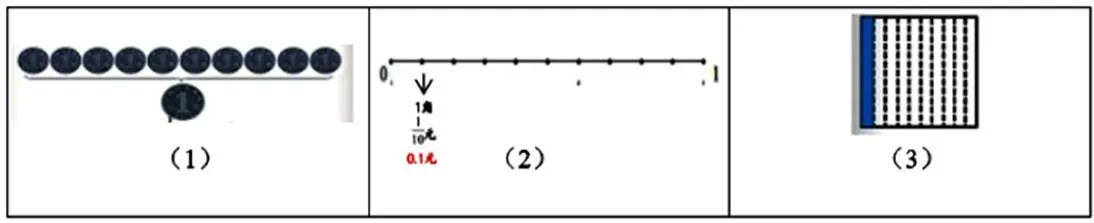
圖1
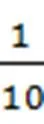
二、以數化形,讓算理算法直觀可見
傳統計算教學的重點僅僅停留在掌握算法、具備一定的運算技能這種較淺顯的層面上,然而這并不是運算能力的全部內容,良好的運算能力應該是運算技能和數學思考的綜合體,是引導學生養成數學核心素養的重要基石。只有讓算理算法更加直觀可見,才能讓教學的重點得到明確,將數學課程中的抽象知識能夠更加直觀地展現出來,教師可以將算理與算法通過實踐進行結合應用,保證學生能夠在閱讀題目的第一時間探尋到題目的真正內涵,讓學生能夠通過不同算法的復合運算,尋找到合理的數學問題解決途徑,這樣才能有效地提升數學問題解決的速度,將更多的數學理念進行融會貫通,讓學生尋找到最合適的解題路徑。學生掌握算法的前提是要讓其理解算理,使學生積極探索其中蘊含的數學原理,達到“知其所以然”的程度,提升自身運算水平。因此,教師在教學過程中要把算理的理解作為教學的重點內容之一,可以采用直觀的幾何圖形闡明抽象的算理內容,借助圖形的直觀性有效地幫助學生充分理解運算的基本道理,為提煉算法做基礎,實現算理與算法融通。
探究:

圖2
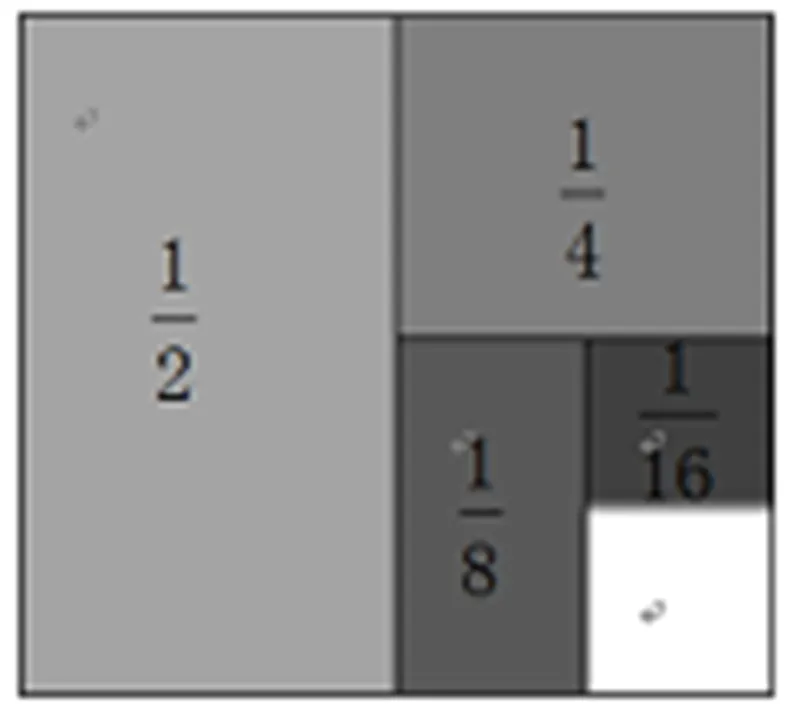
圖3
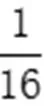
三、以數輔形,讓數學本質更加凸顯
統計圖是一種用直觀圖形表達數據整理統計結果的記錄方式,它充分體現了數形結合思想在實際生活的運用。例如,《折線統計圖》的教學,教師先通過條形統計圖的直條到點再到線的演變,使學生明白折線統計圖是如何產生的,然后再引導學生體會和總結折線統計圖的特點:折線統計圖中用點描述數量的多少,用線來描述數量的增減變化情況。接著引導學生思考:觀察折線統計圖時是否只需要關注圖呢?教師隨即給出一幅縱軸缺少數據的反映某市一年氣溫變化的折線統計圖(如下左圖)。讓學生猜測:該折線統計圖反映的是四季分明的杭州,還是四季如春的昆明,還是常年低溫的哈爾濱?學生僅從折線的陡緩判斷,必定認為是四季分明的杭州。
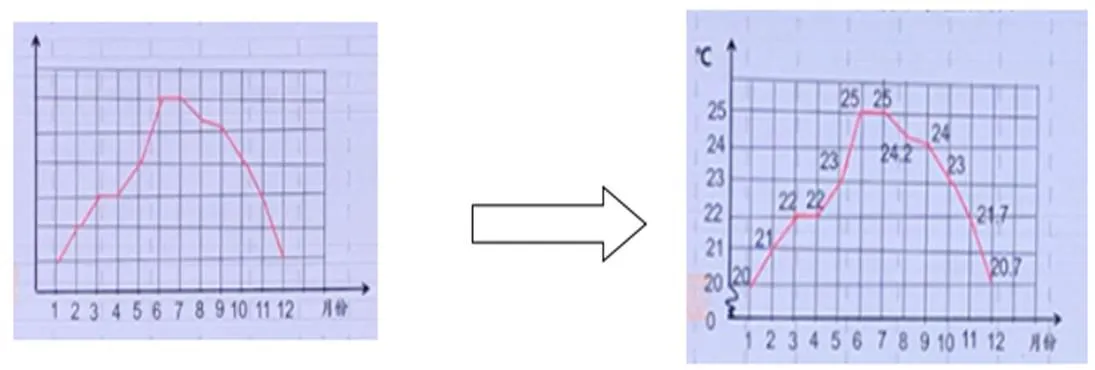
圖4
正當學生脫離數據產生認識偏差時,教師補充縱軸數據(如圖4右),學生立馬感受到單看線的陡緩是不夠準確,需要結合數據進行判斷,真正體會“形少數時難入微”。接著啟發學生思考,怎么讓人一看就能準確判斷出該折線統計圖反映的四季如春的昆明的一年溫度,學生自然想到修改縱軸數據,讓折線更平穩一些,把左圖變成右圖形式。
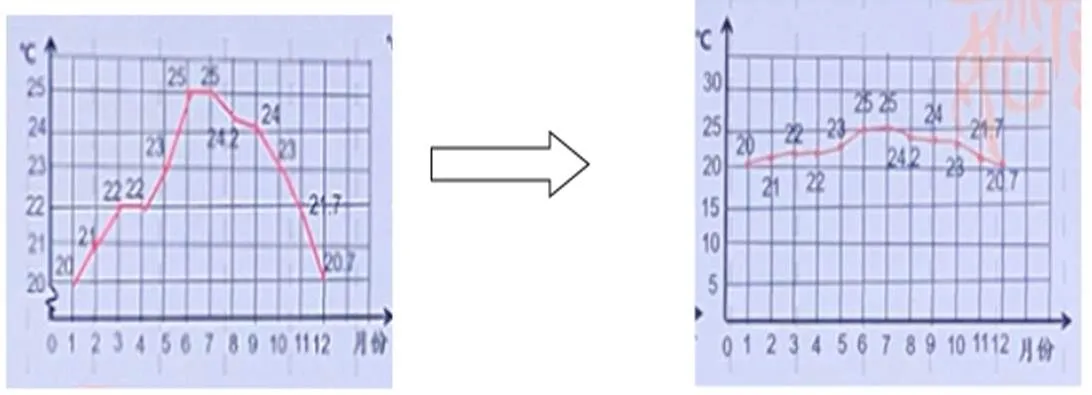
圖5
(氣象提醒:我市氣溫變化比往年要大,請廣大市民留心關注氣溫變化。)
(旅游宣傳:這里四季如春,氣候宜人,歡迎您來昆明。)
最后,通過昆明旅游局和氣象局從統計的功能性出發,對兩幅折線統計圖進行了不同的選擇,使學生感受繪制統計圖時數形結合的必要性,深刻理解統計圖的本質與作用。
四、數形結合,讓解決問題直觀形象
解決問題是小學數學課程的重要內容。傳統的應用題教學,教師多是采用題海戰術,往往導致學生生搬硬套、思維僵化,一旦數量關系變化就可能束手無策。教師在數學問題的教學過程中要時刻提醒學生用“數形結合”的思想解決問題,當遇到復雜的數學問題時要讓學生自己嘗試著畫出圖形,將題目條件通過幾何圖形展現出來,以此尋找解題的突破口。所以當前的數學教學課程中需要一種有效的方法將一些復雜的知識進行轉化,將更多抽象的條件以直觀的形式讓學生進行觀察,這樣才能真正提高學生解題的能力,讓學生的解題速度得到全面的提升。在當前的教學課中應當嘗試將這些題目中的關鍵信息表現出來,讓學生能夠精準地抓住數學問題的重點,找到高效率的解題方式,讓更多學生能夠通過這種方法快速尋找到解題的關鍵要素,在腦海中構建起完整的數學模型。通過這種教學方法,可以讓學生的解題能力達到優化,學生也能夠通過這種教學方法提升自身的學習能力,讓他們養成自主探究的習慣。將題目中的文字條件轉變成直觀清晰的幾何圖形,采用“數形結合”方法輔助學生梳理題目中的數量關系,深入理解題目含義,找到解決問題的關鍵突破口,有效構建數學模型,解決問題能力自然會獲得提升。
例如,行程問題的基本數量關系是“速度×時間=路程”,對此學生雖然熟悉,卻因為運動物體數量、時間、地點、方向、運動結果的變化,構成的問題數量關系多種多樣,學生解題時常常不知從何下手。教師如果能引導學生依題意畫圖,借助幾何直觀,通過數形結合,就比較容易理解題中的數量關系,找到解決問題的策略。以如下題目為例:已知A、B兩地之間的距離為300千米,現在,甲車和乙車同時出發且甲車速度:乙車速度=4:3,其中甲車每小時走過的路程為80千米,問2小時后兩車相距多少千米?本題沒有規定兩車的運動方向,是道開放題,學生能夠借用如下的畫圖策略(如圖6),可以很好地理解有三種運動情況。

圖6
(1)兩輛車分別從A、B兩個位置相對(相向)行駛。
數量關系式:A、B兩地的距離-兩車已行路程之和=兩車相距的距離
300-(80+60)×2=20(km)
(2)甲、乙兩車在同樣的位置朝著同一方向出發。
數量關系式:甲車走過的路程-乙車走過的路程=兩車相距的距離
80×2-60×2=40(km)
(3)甲、乙兩車在同樣的位置朝著相反的方向出發。
數量關系式:甲車走過的路程+乙車走過的路程=兩車相距的距離
80×2+60×2=280(km)
在解決此類路程問題時,線段圖是一種非常有效的輔助工具,學生可以畫出線段圖分析車輛的行駛路程,明確三種不同運動方向,甲、乙兩車2小時后的位置關系,逐個厘清蘊含的數量關系。采用“數形結合”的數學思想分析數學問題、探究題目結果可以幫助學生更好地理解題目意義,打開學生解題思路,培養學生的數學思維。
華羅庚先生曾說過:“數形結合有百般的好處。”這就深刻地闡明了“數形結合”這一重要數學思想的重要性和優勢所在。在日常的數學教學中,只要教師注重引導學生利用“數形結合”的思想分析、研究數學問題的解題思路和技巧,化抽象為具體,就一定能夠幫助學生挖掘題目中的隱含信息,打開學生的解題思路,引導學生積極主動地探索問題結果,學生的數學學習定會走向深刻,實現深度學習。在我國的數學教學課堂上最常見的問題便是教師的教學方法并不合理。對于數學教學工作而言,這些教學方法很難讓學生產生對數學的興趣,如果學生缺少興趣很容易失去學習的動力,所以教師應當以學生的興趣激發進行課程的設計,降低數學學習的門檻,讓學生能夠將一些復雜的理論知識用簡單明了的幾何圖形進行展現,這樣更有利于激發學生的學習欲望,讓他們能夠在自主探究的模式下高效率地進行學習。教師應當根據學生的特點設計出更加完善的教學方案,讓更多學生能夠利用數形結合的方法梳理題目中的數量關系,并且將自己所學的解題方式帶入題目當中,讓學生的學習水平得到全面的提升,學生能夠更加靈活地運用知識解決問題,將更多復雜的知識以直觀的形式進行解答,實現學習水平的全面提升。
[1] 宋梅娟.數缺形時少直觀,形少數時難入微[J].明日,2018(19).
[2] 徐惠.合理“嫁接”數與形促進學生數學理解[J].小學教學設計,2014(29).
[3] 林文清.幾何直觀在“數與代數”教學中的巧妙運用[J].青海教育,2018(10):2.
[4] 袁曉萍.讓數據分析成為一種思維習慣——“統計里的秘密”教學實踐與思考[J].小學數學教育, 2018(12).
G622
A
1002-7661(2022)11-0151-03

