基于電磁軸承單元的銑削力在線測量方法
萬少可,奚航航,李小虎,閆柯,洪軍
(1.西安交通大學,西安 710049;2.現代設計與轉子軸承系統教育部重點實驗室,西安 710049)
在銑削加工過程中,刀具狀態的改變(正常、磨損、崩刃、斷齒等)會直接引起銑削力的變化,從而影響工件的加工質量。盡管可以通過小波包變換等現代信號處理方法或支持向量機等機器學習算法對振動、電動機電流或功率等信號進行處理從而間接地進行刀具狀態評估,但學術界普遍認為基于銑削力信號的刀具狀態評估更加精準和可靠[1]。因此,實現銑削過程中銑削力的在線測量對實現刀具狀態精準評估,提高銑削加工質量具有重大意義。
目前,常使用三向測力儀等設備進行銑削力測量[2],但此類設備成本昂貴且對工件安裝尺寸有要求,主要應用于科學試驗研究等場合,在實際銑削加工過程中的應用具有顯著的局限性。基于這一原因,廣大學者進行了集成于機床結構或刀具中的力測量模塊設計,如文獻[3]利用壓電元件研制了高精度切削力自感知智能車刀,其與機床兼容性好,方法簡單且成本低,但并不適合刀具高速旋轉的銑削加工,如何高效地進行銑削力的在線測量依舊是銑削加工領域需要解決的重大問題。
電磁軸承作為一種包含位置傳感器與控制器的主動可控式軸承,不僅可以用于支承主軸轉動,也可以作為集成于主軸系統中的傳感器,在線獲取主軸位移信息。文獻[4]設計了用于鏜削加工過程中鏜刀桿振動抑制的電磁式主動阻尼裝置,基于卡爾曼濾波器狀態估計原理,利用線圈控制電流以及反饋位移信號實現了鏜削力的間接測量。因此,本文嘗試在銑削加工主軸系統中集成電磁軸承單元,利用其特性實現銑削力的在線測量。
1 銑削力測量原理
為實現銑削力的在線測量,需要將電磁軸承集成于主軸系統中。電磁-滾動軸承混合支承主軸系統如圖1所示,其由電磁軸承和2套角接觸球軸承混合支承,角接觸球軸承作為主支承,電磁軸承位于主軸前端靠近刀柄處,作為輔助支承。電磁軸承是在線測量銑削力的關鍵單元,由轉子鐵芯、繞有線圈的定子鐵芯和電渦流位移傳感器等構成,工作原理[5]如圖2所示。
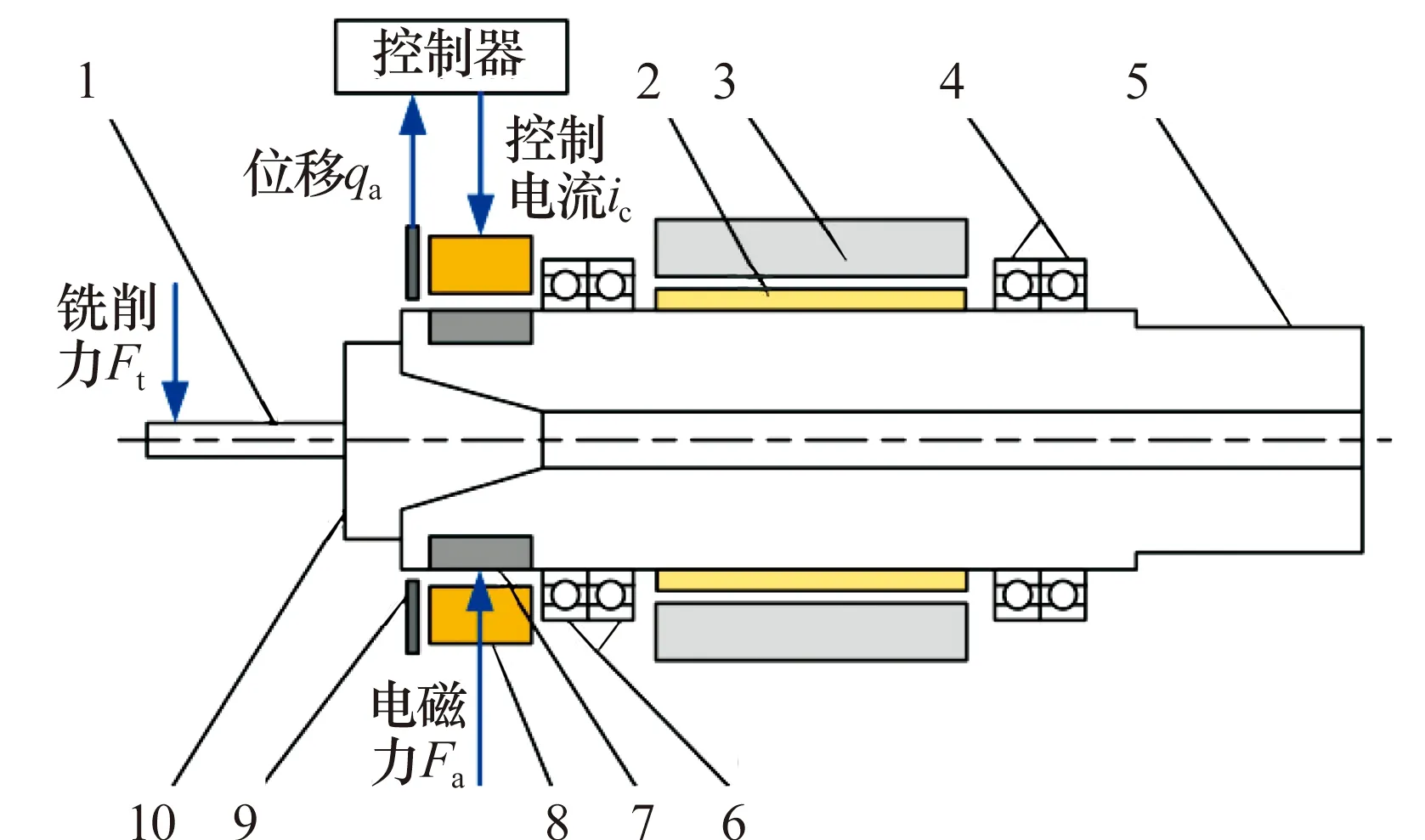
1—刀具;2—主軸電動機轉子;3—主軸電動機定子;4—后軸承組;5—轉軸;6—前軸承組;7—轉子鐵芯;8—繞有線圈的定子鐵芯;9—電渦流傳感器;10—刀柄。
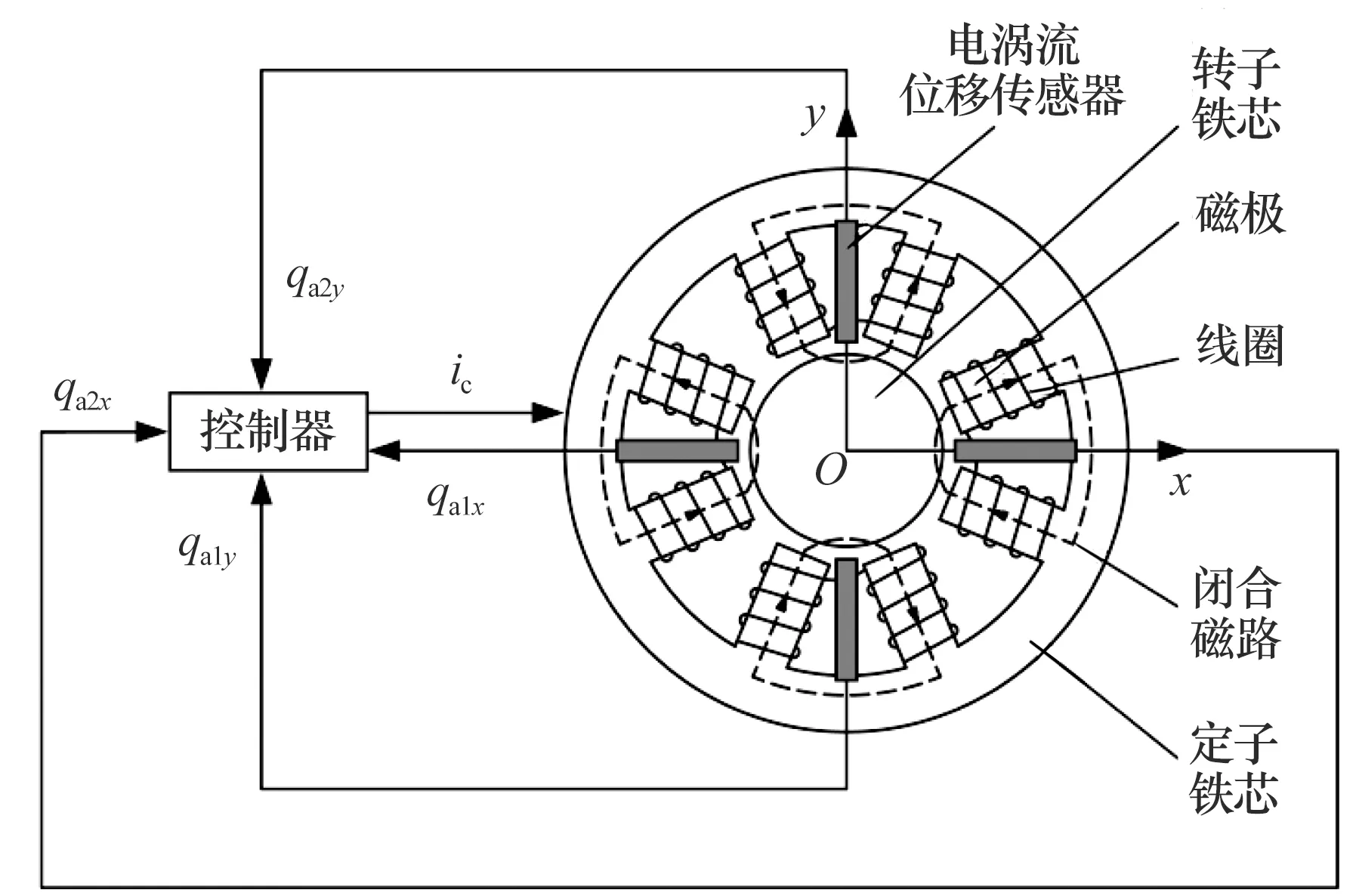
圖2 電磁軸承工作原理示意圖Fig.2 Schematic diagram of AMB
加工過程中,在銑削力Ft的作用下,主軸產生徑向振動位移qa(圖1),電渦流傳感器實時捕獲這一位移并將其輸入到電磁軸承控制器中,控制器通過輸入線圈中的控制電流信號ic產生一個主動電磁力Fa,推動主軸往qa的反方向運動,從而抵消徑向振動位移。由此可見,控制電磁軸承所需的主軸位移信號以及控制電流信號均與銑削力有內在關系,本文嘗試在電磁-滾動軸承混合支承主軸系統的基礎上融合電磁軸承位移信號和控制電流信號實現銑削力的在線測量(圖3),從而助力于銑削加工過程中刀具狀態精準評估的實現。
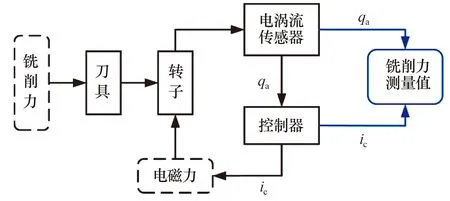
圖3 銑削力測量原理Fig.3 Schematic diagram of milling force measurement
2 數學模型
2.1 電磁軸承
2.1.1 轉子位移
電磁軸承單元中,4個電渦流位移傳感器兩兩一組,分別布置在x,y方向上,用于測量轉子在xOy平面內的位移大小和方向。
以y方向為例,設電渦流位移傳感器與轉子表面的初始距離為qa0y,在某一次振動中,2個傳感器測得的距離值分別為qa1y和qa2y,則轉子在y方向的位移為
(1)
同理可求得轉子在x方向的位移qax。
2.1.2 電磁力
本文使用的電磁軸承在周向對稱分布了8個磁極,每相鄰的2個磁極(夾角為α)形成一個磁極對,2個對稱分布的磁極對形成差動磁極對。同樣以y方向為例,由電磁軸承工作原理可知電磁力為
Fay=kiic+kss,
(2)
(3)
(4)
(5)
式中:ki為電流剛度系數,N·A-1;ic為線圈控制電流,A;ks為位移剛度系數,N·m-1;s為定子鐵芯與轉子鐵芯間的氣隙變化量,m;i0為線圈偏置電流,A;c0為定子鐵芯與轉子鐵芯間的氣隙,m;μ0為真空磁導率,取4π×10-7H/m;A為磁路的橫截面積,m2;N為磁極對線圈的匝數。
聯立(2)—(5)式即可求得電磁軸承在y方向上輸出的電磁力Fay,同理可求得電磁軸承在x方向上輸出的電磁力Fax。
2.2 滾動軸承
考慮到求解精度和速度,本文采用滾動軸承擬靜力學模型進行求解。軸承在軸向載荷Fx,徑向載荷Fy和Fz,彎矩My和Mz的作用下(圖4),內、外圈之間產生軸向相對位移δx,徑向相對位移δy和δz,角相對位移θy和θz。基于赫茲接觸理論和滾道控制理論建立角接觸球軸承的五自由度擬靜力學模型[6],則軸承剛度矩陣KB可表示為
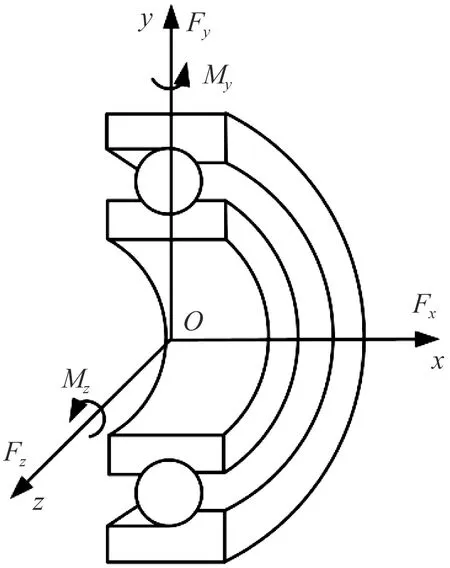
圖4 角接觸球軸承受力示意圖Fig.4 Force diagram of angular contact ball bearing
(6)
F=[Fx,Fy,Fz,My,Mz]T,
(7)
d=[δx,δy,δz,θy,θz]。
(8)
2.3 主軸
電主軸具有軸對稱結構,運用二維梁單元對轉軸進行建模即可滿足求解精度,典型Timoshenko梁單元的結構如圖5所示,其由2個節點組成,每個節點有5個自由度,包括3個平動自由度δx,δy,δz以及2個繞徑向的轉動自由度θy,θz。節點1的位移向量為[δx1,δy1,δz1,θy1,θz1],節點2的位移向量為[δx2,δy2,δz2,θy2,θz2]。
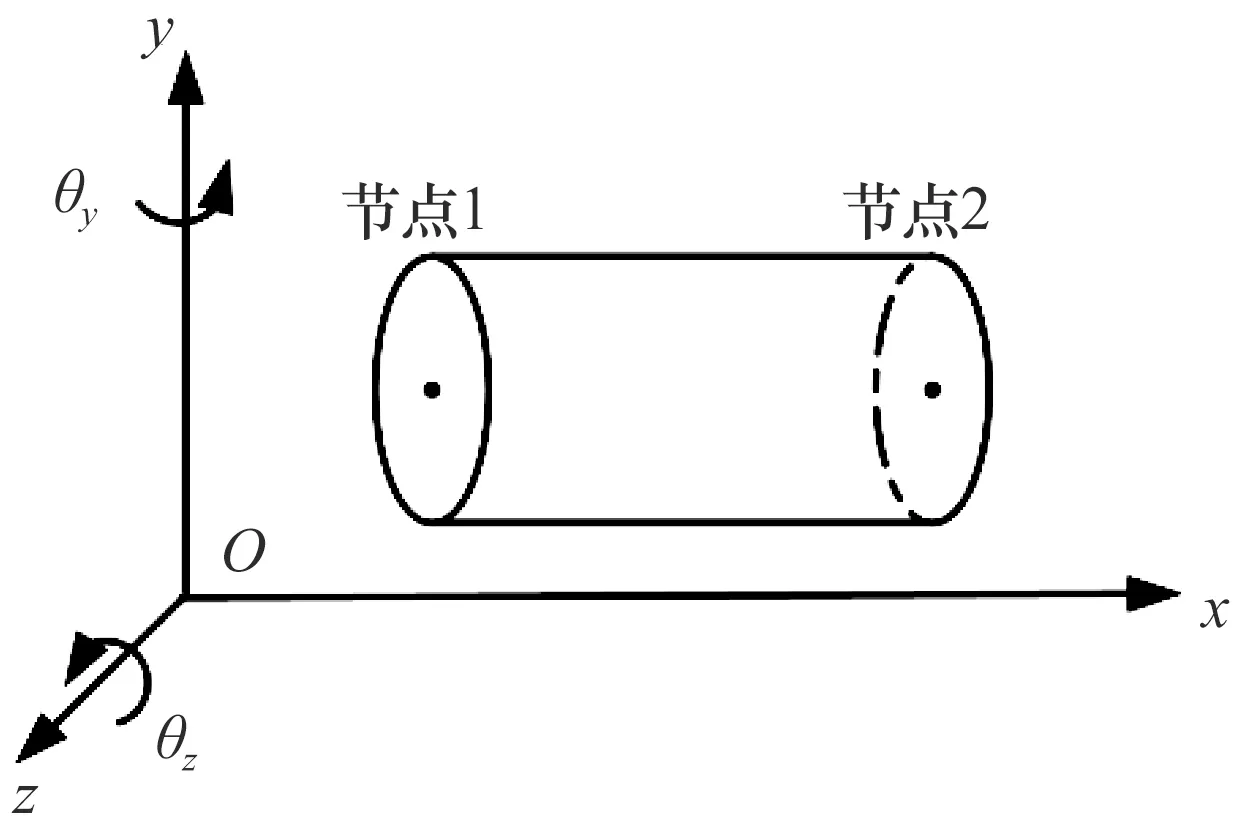
圖5 梁單元有限元模型Fig.5 FE model of beam
忽略梁單元內部阻尼,由拉格朗日方程可得梁單元的運動方程為
(9)
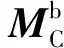
2.4 混合支承主軸系統
基于有限元思想,根據上述的梁單元模型建立轉軸模型,通過剛度耦合方式將角接觸球軸承五自由度擬靜力學模型耦合到轉軸有限元模型中,通過力耦合方式將電磁軸承模型耦合到滾動軸承-轉子有限元模型中,最終建立的混合支承主軸系統動力學模型可表示為
(10)
式中:M為主軸質量矩陣;u為主軸位移矩陣;C為主軸阻尼矩陣;G為轉軸陀螺矩陣;K為轉軸剛度矩陣;MC為離心效應引起的轉軸附加質量矩陣;KB為角接觸球軸承剛度矩陣;F(t)為外力矩陣,包括銑削力Ft和主動電磁力Fa。
2.5 銑削力推導
2.5.1 電磁軸承閉環控制
對電磁軸承建立PD控制器[7],控制電流為
(11)
qa=TqFFt,
(12)
式中:KP,KD分別為PD反饋控制器的增益反饋系數、微分反饋系數;qa為電渦流位移傳感器測得的主軸徑向位移,m;Ft為銑削力,N;TqF為電磁軸承閉環控制時qa與Ft之間的傳遞函數。
采用閉環控制時,銑削力為
(13)
2.5.2 電磁軸承開環控制
解開PD控制環,此時主動電磁力Fa的大小由氣隙變化量直接影響,則
qa=GqFFt+Gqiic,
(14)
式中:GqF為電磁軸承開環控制時qa與Ft之間的傳遞函數;Gqi為電磁軸承開環控制時qa與ic之間的傳遞函數。
采用開環控制時,銑削力為
(15)
3 仿真分析
基于第2節中的數學模型,利用Matlab軟件編程并進行仿真分析,其中電磁軸承參數見表1,銑削力模擬輸入值如圖6所示。
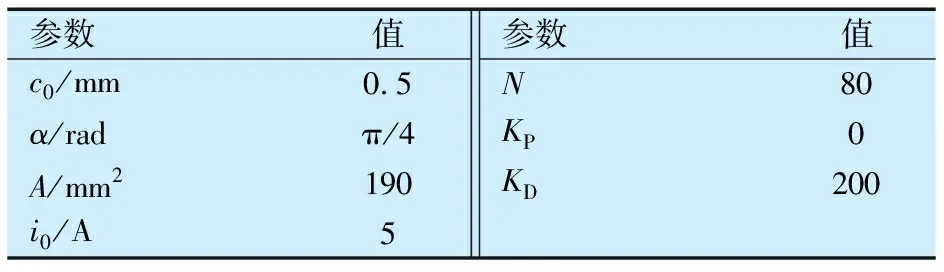
表1 電磁軸承參數Tab.1 Parameters of AMB
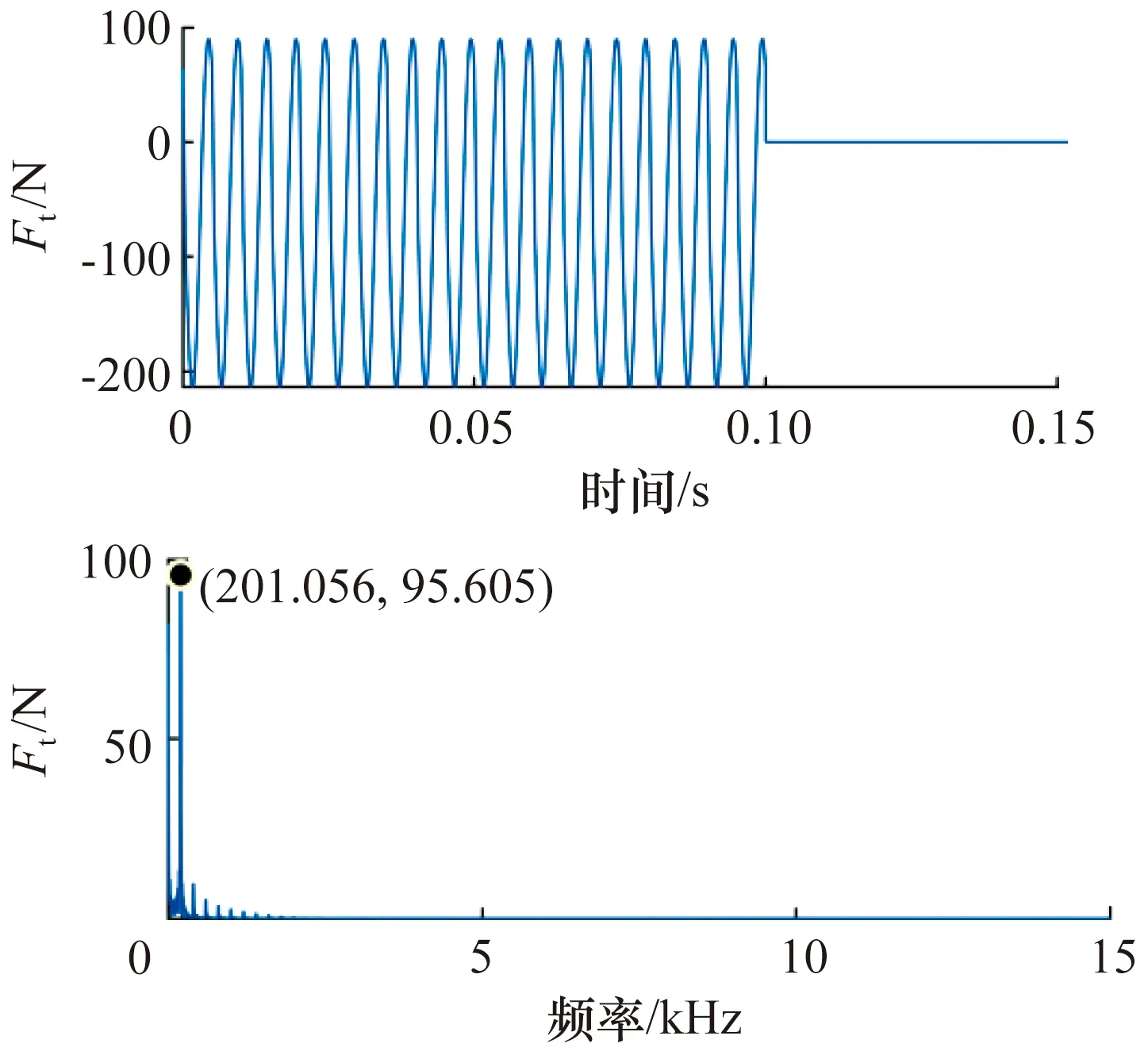
圖6 銑削力模擬輸入值Fig.6 Simulation input value of milling force
由于主軸系統及電磁軸承單元在結構上具有對稱性,選擇x或y任一方向進行仿真即可,另一方向同理。本文以y方向為例進行仿真分析。
3.1 電磁軸承閉環控制
電磁軸承閉環控制時用位移信號計算銑削力。采用向刀尖施加脈沖激勵的方法確定電渦流位移傳感器處主軸位移信號qay與刀尖銑削力Fty之間的閉環傳遞函數TqF,結果如圖7所示。
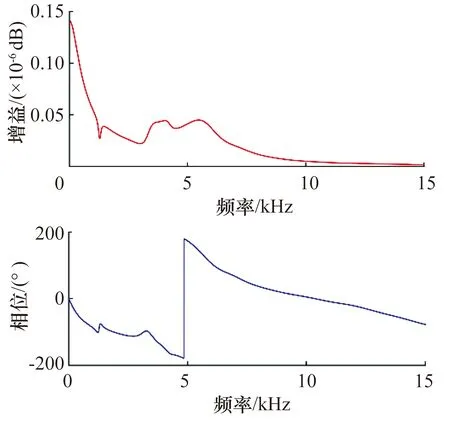
圖7 電磁軸承閉環控制時qay與Fty之間的傳遞函數TqFFig.7 Transfer function TqF between qay and Fty inclosed-loop control of AMB
將銑削力模擬輸入值施加到刀尖,根據(13)式,利用位移信號qay進行銑削力計算,結果如圖8所示。對比銑削力Fty的測量值與輸入值,繪制誤差曲線如圖9所示,除銑削開始和結束時刻附近的誤差較大外,誤差始終保持在-2.2~1.0 N范圍,相對誤差不超過1%,該方法理論上可行。
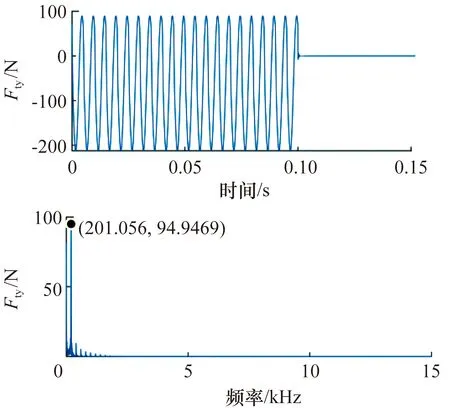
圖8 閉環控制條件下銑削力測量值Fig.8 Measured value of milling force underclosed-loop control
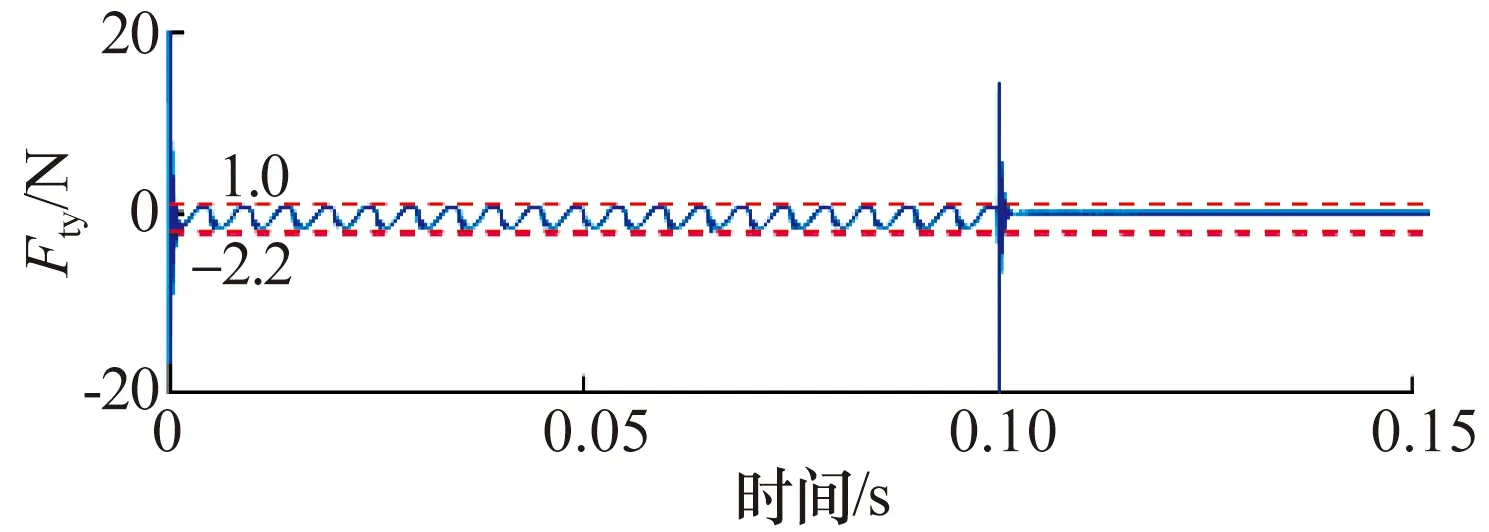
圖9 閉環控制條件下銑削力測量誤差Fig.9 Measurement error of milling force underclosed-loop control
3.2 電磁軸承開環控制
電磁軸承開環控制時用位移信號qay和控制電流信號ic計算銑削力。采用從刀尖輸入脈沖激勵的方法,確定電渦流位移傳感器處主軸位移信號qay與刀尖銑削力Fty之間的開環傳遞函數GqF,結果如圖10所示。
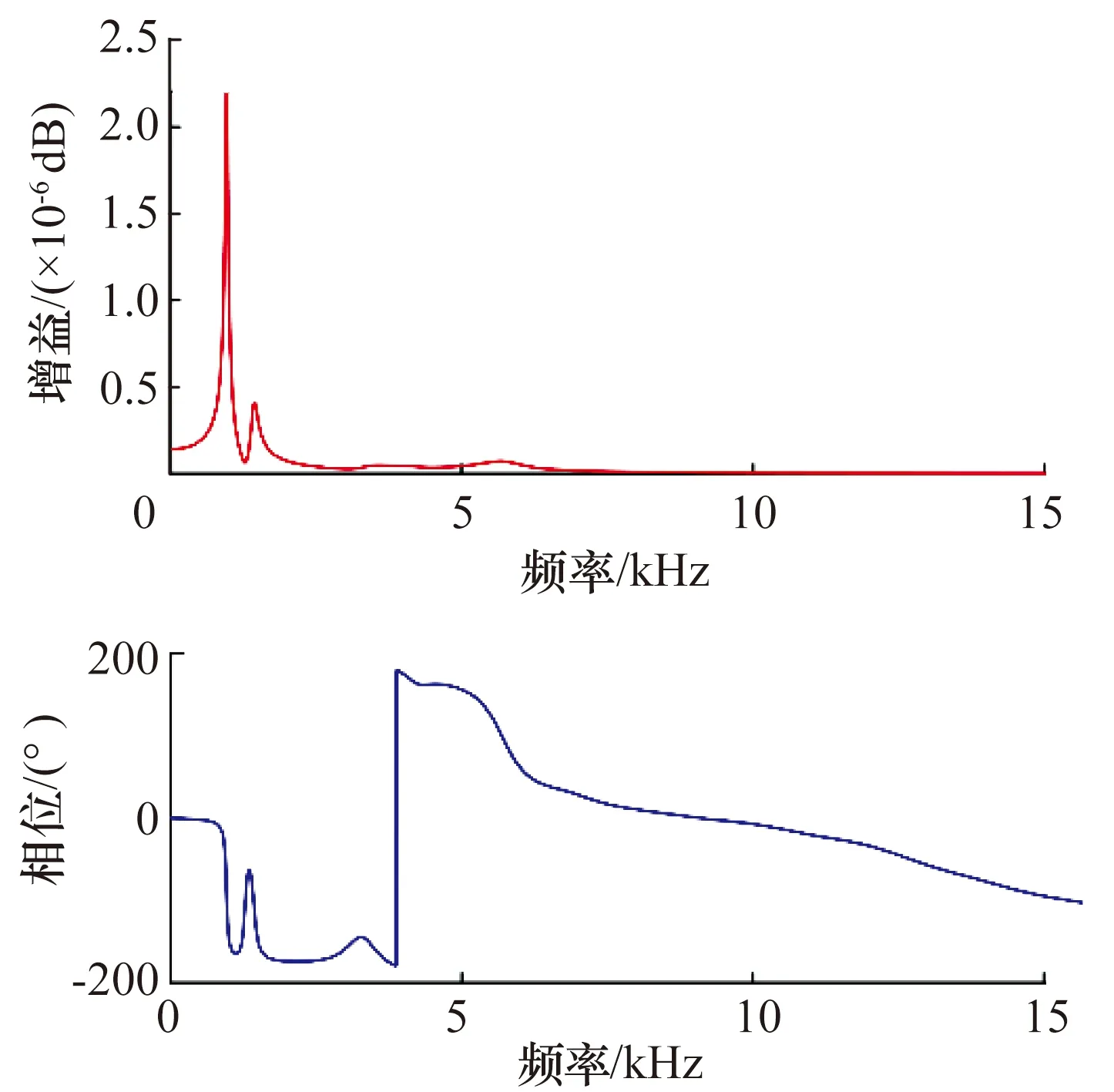
圖10 電磁軸承開環控制時qay與Fty之間的傳遞函數GqFFig.10 Transfer function GqF between qay and Fty inopen-loop control of AMB
通過電磁軸承控制器產生掃頻控制電流(頻率范圍為1~2 000 Hz)對主軸施加掃頻力激勵,確定電渦流位移傳感器處主軸位移信號qay與電磁軸承控制電流ic之間的開環傳遞函數Gqi,結果如圖11所示。
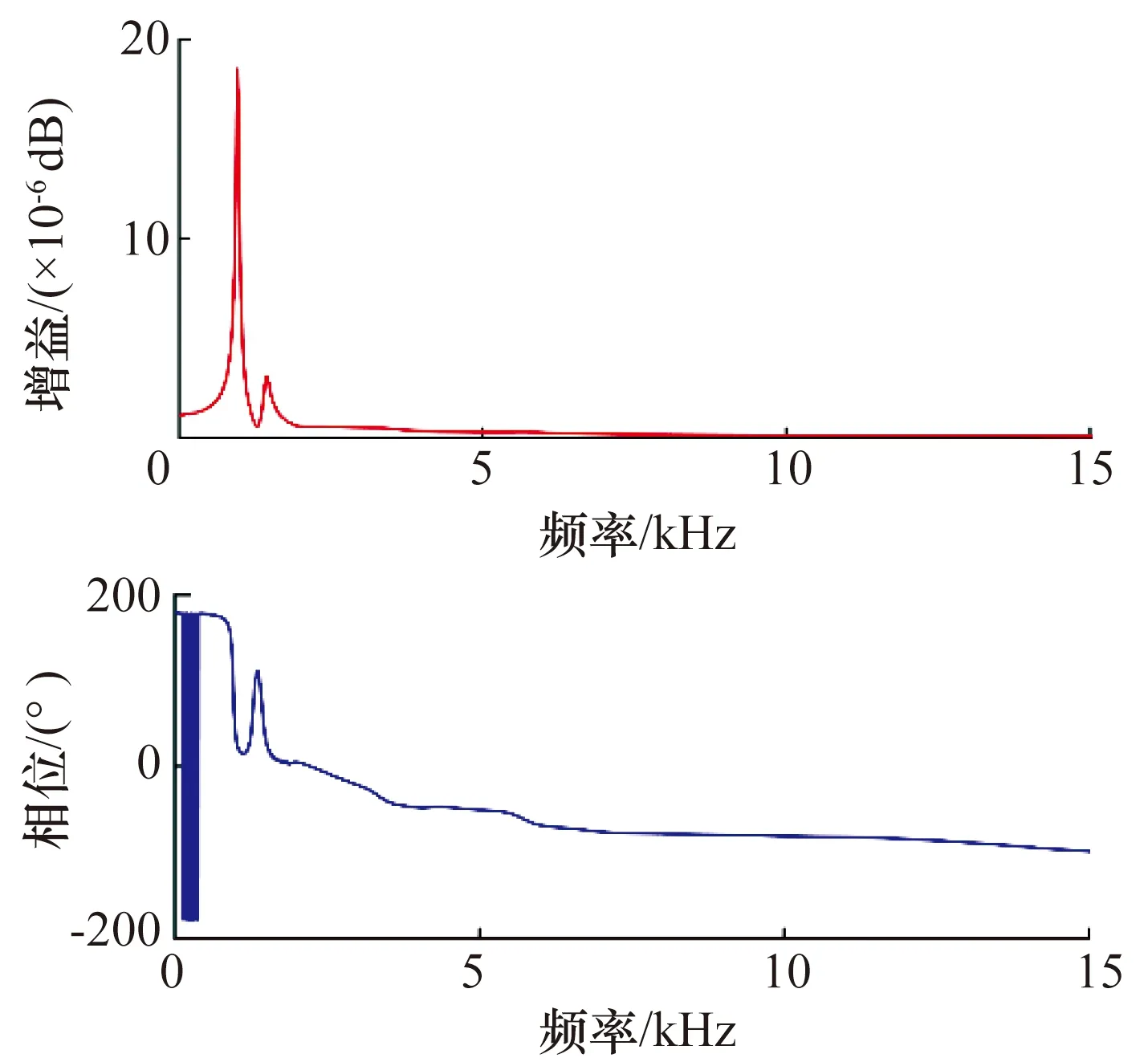
圖11 qay與ic之間的開環傳遞函數GqiFig.11 Open-loop transfer function Gqi between qay and ic
將銑削力模擬輸入值施加到刀尖,根據(15)式,利用位移信號qay和控制電流信號ic進行銑削力計算,結果如圖12所示,銑削力Fty的測量值與輸入值的誤差曲線如圖13所示,除銑削開始和結束時刻附近的誤差較大外,誤差曲線始終保持在-1.8~1.0 N范圍,相對誤差不超過1%,同樣證明該方法理論上可行。
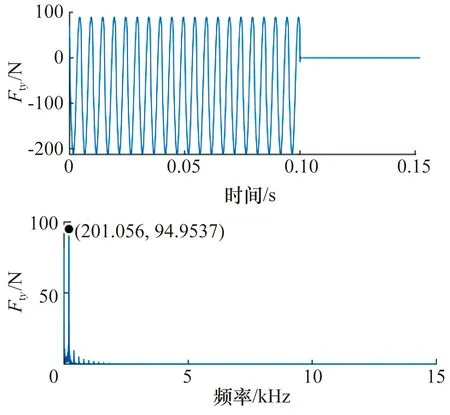
圖12 開環控制條件下銑削力測量值
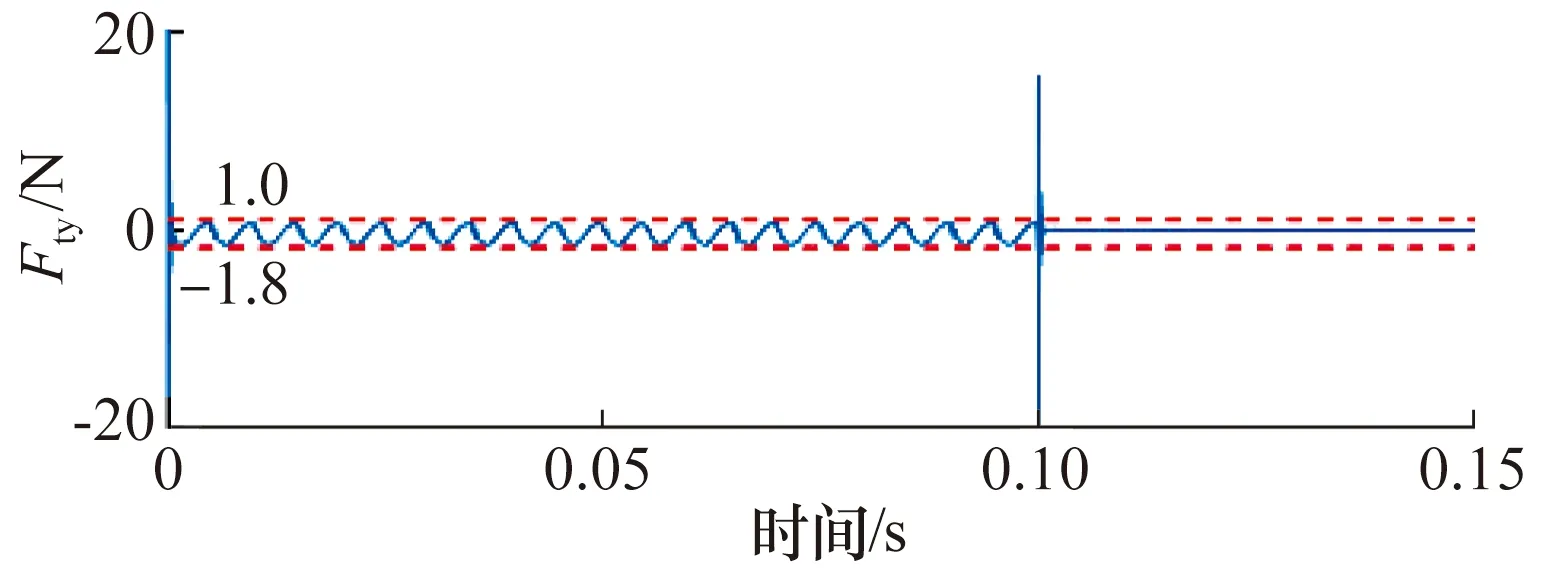
圖13 開環控制條件下銑削力測量誤差Fig.13 Measurement error of milling force underopen-loop control
4 結束語
構建了電磁-滾動軸承混合支承主軸系統并建立了有限元模型,根據電磁軸承控制原理推導了銑削力在線測量表達式,Matlab軟件仿真分析結果顯示銑削力測量值與輸入值之間的相對誤差不超過1%,該方法理論上可行。
相比于傳統的基于測力儀的銑削力測量方法,本方法對工件的安裝無要求且成本更低,更適合實際加工過程。在未來的研究中將對本文所提方法進行試驗驗證,基于獲得的銑削力信號進行刀具狀態評估方法研究,以提高銑削加工質量,推進高速銑削電主軸智能化的進程。

