基于電磁力的轉子不平衡-不對中振動靶向抑制

暴一帆，國玉林，姚劍飛

(北京化工大學 機電工程學院，北京 100029)

旋轉機械是現代工業的重要設備，其穩定性直接影響企業的生產安全和經濟效益。旋轉機械轉子系統運行環境惡劣，受多種激勵源的作用，振動故障耦合嚴重，振動成分復雜且噪聲較大，若不及時有效抑制轉子振動，故障會進一步惡化，從而導致事故的發生。

主動磁軸承因具有無接觸、無摩擦、無潤滑、無密封、低功耗等特點，常作為執行機構用于轉子振動的主動控制[1]。國內外學者在利用電磁力抑制旋轉機械轉子系統振動方面做了大量研究。轉子不平衡振動(以工頻振動為主)抑制方面：文獻[2]提出一種結合新型自適應陷波濾波器的前饋控制策略解決磁懸浮離心壓縮機轉子不平衡問題；文獻[3]設計實時變步長多邊形迭代搜尋算法的不平衡補償器抑制轉子振動；文獻[4]提出一種基于幅值和相位特征的不平衡力快速尋優前饋算法；文獻[5]提出了一種基于電磁作動器(Active Magnetic Actuator，AMA)的比例-微分(Proportional Differential，PD)反饋控制算法抑制轉子不平衡引起的基頻振動。轉子不對中故障(以工頻、二倍頻為主的復合振動)或多頻振動抑制方面：文獻[6-7]通過變步長尋優策略得到電磁作動器所需的最佳電流，向轉子施加多頻率成分電流實現轉子多頻振動前饋抑制；文獻[8]通過電流補償算法有效抑制了轉子系統的多頻振動；文獻[9]參考不平衡試算法，從理論仿真方面提出了一種不對中故障的試算方法。

文獻[2-4]均基于前饋算法對轉子不平衡故障進行主動抑制，抗擾動能力及控制穩定性差，文獻[5]PD反饋控制算法穩定性優異，但在惡劣工況及全頻隨機噪聲的影響下控制精度較低，缺少振動抑制的靶向性，此外，PD算法主要用于單一頻率、單一故障抑制，有必要考慮PD算法抑制轉子振動的靶向性，對其在多頻率、多故障的振動抑制進行研究。

振動靶向抑制方面：文獻[10]提出靶向抑制概念，即通過分析故障的機理和特征，找準故障靶點，以采取相應措施精準抑制轉子振動；文獻[11]闡述了透平機械系統中的振動靶向抑制，分析了透平機械轉子-軸承系統中轉子的多頻率成分振動的靶向抑制；文獻[12]針對旋轉機械氣壓液體式不平衡振動故障，利用氣壓液體式自動平衡裝置搭建了靶向自愈調控系統。

本文基于文獻[10-12]的靶向抑制思路，將其應用到基于AMA的PD控制策略，以抑制轉子不平衡和不對中耦合故障。采用AMA作為控制執行機構，設計了基于電磁作動器的PD算法控制器，以抑制旋轉機械轉子系統不平衡-不對中耦合故障引起的周期振動。

1 系統建模

1.1 動力學建模

基于有限元法建立轉子-軸承-AMA系統(圖1)動力學模型，即

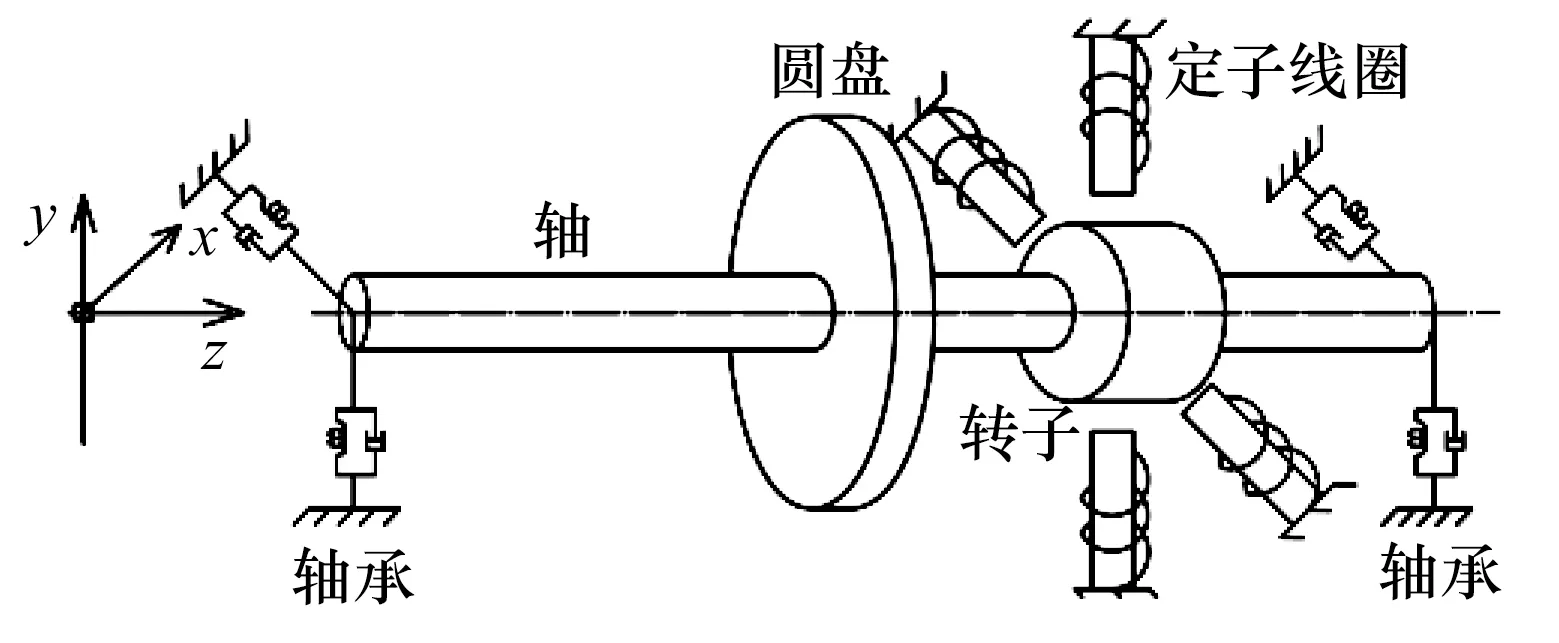
圖1 轉子-軸承-AMA系統示意圖Fig.1 Diagram of rotor-bearing-AMA system

(1)

式中：M,C,K分別為系統的質量矩陣、阻尼矩陣和剛度矩陣;Z為位移列向量;F1為廣義干擾力，包含不平衡力Fd和不對中力Fc；F2為主動控制力,包含電磁力Fmag。

圓盤結點處所受不平衡力如圖2所示，O為轉軸形心，O1為圓盤形心，不平衡力可表示為

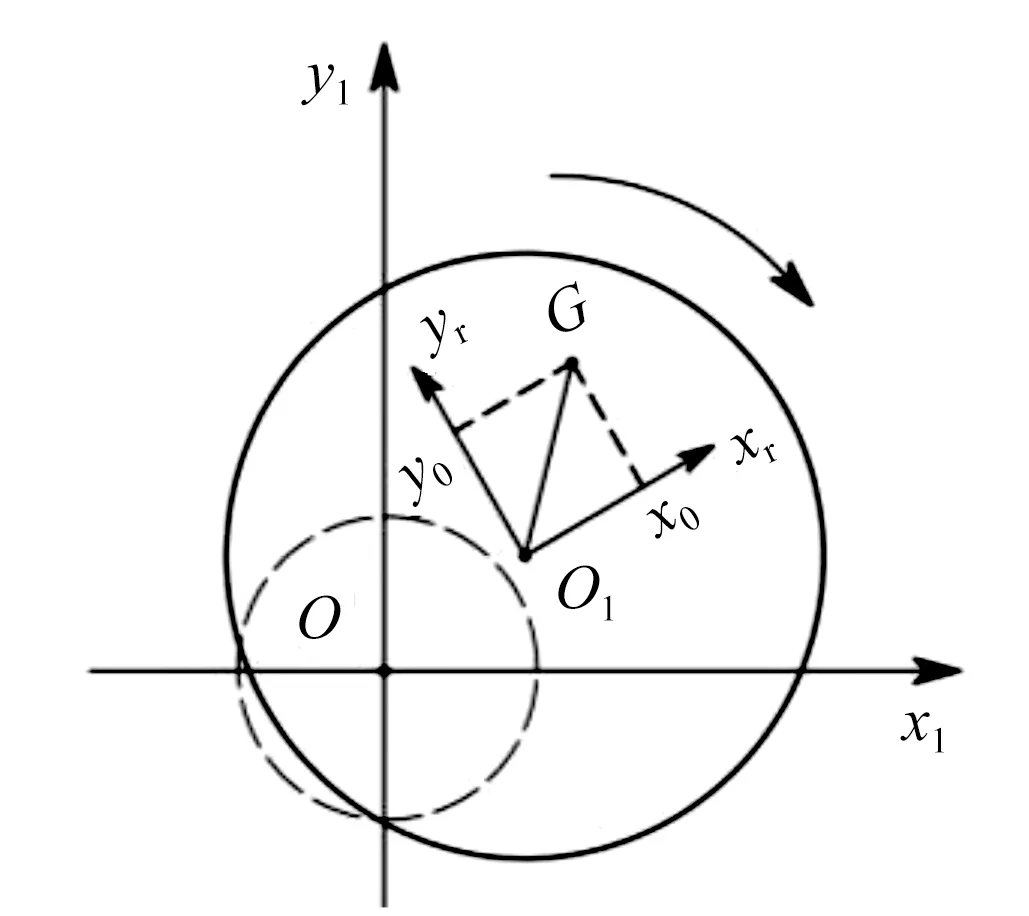
圖2 轉子不平衡示意圖Fig.2 Diagram of rotor unbalance

(2)

式中：md為圓盤偏心質量；ω為轉子角速度；t為時間；(a0，b0) 為質心坐標。

考慮軸系連接處的平行不對中力，以二倍頻為主，采用等效軸段法建立聯軸器模型，如圖3所示，O2為轉軸對應半聯軸器的形心，O3為電動機對應半聯軸器的形心，A為半聯軸器和聯軸器中間軸的螺栓連接點。令不對中偏差量坐標為(δx，δy)，聯軸器徑向剛度取Kc，不對中力可表示為[13]

圖3 聯軸器平行不對中示意圖Fig.3 Diagram of coupling parallel misalignment

(3)

采用12極E型結構AMA，其y方向結構如圖4所示，y方向上下電磁力合力可表示為

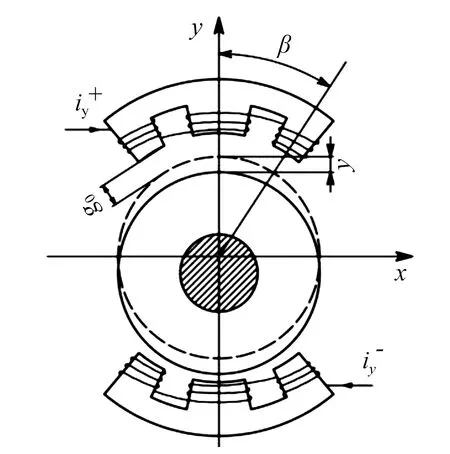
圖4 AMA y方向結構圖Fig.4 Structure diagram of AMA along y direction

(4)

ka=49μ0N2A02(1+cosβ)/128，

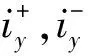
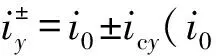
(5)

Ks=4kai02/g03，

Ki=4kai0/g02，

式中：Ks為位移剛度；Ki為電流剛度。

假設x，y方向氣隙均勻，磁極面積相同，忽略2個方向的磁場耦合和漏磁，可認為2個方向位移剛度和電流剛度相等，則

-Ksza+Kiic,

(6)

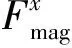
干擾力和控制力需要通過變換矩陣將局部坐標系下的力轉換至整體坐標系下，即變換成與 (1) 式階數相同的矩陣。以電磁力為例，通過變換矩陣Tc可得

(7)

對(1)式變化可得

(8)

新的剛度矩陣可表示為

(9)

1.2 狀態空間方程

為便于求解運動方程的瞬態解，將上述的有限元方程轉換為狀態空間方程，定義狀態空間向量為

(10)

(11)

將(11)式轉化為一階微分方程形式，代入(10)式可得

(12)

Bsu=[0M-1]T，

式中：As為系統矩陣；Bsa，Bsu分別為電磁作動器電流和干擾力的輸入矩陣。

2 控制律及濾波器設計

考慮旋轉機械系統的多頻振動，將振動故障的靶點表示為[11]

Θ(EN1,EN2,…,ENn;IN1,IN2,…,INn;QN1,QN2,…,QNn)，

(13)

式中：EN為能量流層面的特征參數(如執行機構的驅動能量等)；IN為信息流層面的特征參數(如控制系統中的參數信息等)；QN為物質流層面的特征參數(如系統中的介質等)。

結合旋轉機械中能量流、信息流和物質流的特征，搭建旋轉機械實時狀態監測系統，采用多頻振動響應的特征頻率、幅值、相位等參數來表征振動故障靶點，針對試驗臺實時頻譜瀑布圖中較為突出的工頻和二倍頻，分析其機理，準確定位靶點，有針對性地選擇和設計控制律和濾波器，抑制不平衡和不對中故障引起的多頻振動。

2.1 控制律設計

比例積分微分(Proportional Integration Differentiation，PID)控制屬于經典線性控制器，是最早應用于磁軸承的控制技術。以y方向采樣序號為n時的位移信號y(n)為例，設期望輸出為yd(n)，系統偏差e(n)=yd(n)-y(n)，則PID控制算法的時域控制律為

(14)

式中：kP為比例系數；Ts為采樣時間；kD為微分系數；t為采樣時刻。

考慮到實時控制系統對(14)式離散并整合調整參數后得到離散PID表達式為

(15)

式中：KP為比例增益；KI為積分增益；KD為微分增益。

積分控制主要用于消除系統靜態誤差選取不當易引起的超調或積分飽和，考慮多倍頻周期振動的主動抑制，采用PD控制算法，即令Ki=0，則 (6) 式中局部坐標系下的控制電流為

(16)

式中：KP為比例增益二階對角矩陣；KD為微分增益二階對角矩陣。

將(16)式整合到系統運動方程(8)式中，得到基于PD控制律的系統剛度矩陣K0、阻尼矩陣C0為

(17)

(18)

此時，系統運動方程為

(19)

根據(17)—(19)式，通過調整比例增益和微分增益改變系統剛度和阻尼，以實現控制系統振幅。

2.2 濾波器設計

陷波濾波器采用二階(N=M=2)無限脈沖響應數字濾波器，其遞歸方程為

(20)

式中：ak和bl為多項式系數，考慮到多轉速控制以及精確靶向抑制的需要，多項式系數通過實時轉速和陷波帶寬實時查表確定；yf(n)為n時刻對位移信號y(n)的濾波處理值。

3 仿真分析

3.1 有限元模型

轉子-軸承-AMA系統模型主要參數見表1，根據第1節系統建模公式建立有限元模型，將整個系統劃分為11個Timoshenko梁單元，如圖5所示。設不平衡力作用在圓盤(9#節點)處，平行不對中力作用在聯軸器(3#節點)處，主動電磁控制力施加于AMA(7#節點)處。

圖5 轉子-軸承-AMA系統模型Fig.5 Model of rotor-bearing-AMA system

表1 轉子-軸承-AMA系統模型主要參數

3.2 算法控制效果

仿真過程中，取系統采樣頻率fs=10 kHz，轉

子轉頻f=100 Hz，比例增益KP=4×107，微分增益KD=10，基于MATLAB仿真分析得到AMA 7#節點控制前后的軸心軌跡和頻域曲線如圖6所示：1)在控制器激發后，經過衰減振蕩(收斂過程)，軸心軌跡更趨向坐標原點且保持穩定；2)振幅減小，工頻和二倍頻成分得到顯著抑制。說明該算法對不平衡-不對中耦合振動具有較好的抑制效果。

圖6 AMA 7#節點控制前后的仿真結果Fig.6 Simulation results before and after AMA 7#node control

4 試驗驗證

建立轉子-軸承-AMA系統試驗臺如圖7所示， 1#，2#測點分別裝有2套電渦流位移傳感器，3#，4#測點分別裝有1套電渦流位移傳感器。可傾瓦滑動軸承五瓦均布，且采用瓦塊上承載、中心支承的方式。系統采樣頻率fs為10.24 kHz，其他參數同表1。

圖7 轉子-軸承-AMA系統試驗臺Fig.7 Test rig of rotor-bearing-AMA system

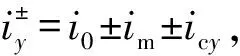
(16)

式中：FG為AMA提供的y方向支承力。偏置電流i0=1 A，試驗中取im=0.1 A。

在多個轉速下對轉子振動進行實時主動抑制以驗證所提算法對轉子不平衡和不對中振動抑制的有效性。采用試湊法選取PD控制器參數：比例增益KPx=KPy= 2×104，微分增益KDx=KDy=15。得到1#測點y方向多轉速控制前后振幅如圖8所示，該算法對不同轉速的轉子振動均有較好的抑制效果，各轉速下轉子振幅降低幅度在43.8%～56.0%之間。當轉速大于1 350 r/min時，振動抑制率減小，說明PD控制算法魯棒性不強。

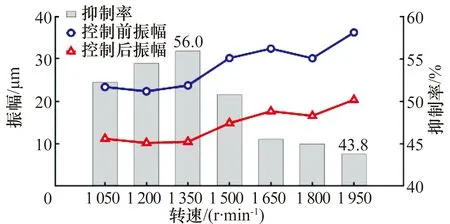
圖8 1#測點y方向振幅多轉速控制對比圖Fig.8 Comparison diagram of amplitude multi speed controlin y direction of 1# measuring point

在轉速為1 950 r/min時各測點試驗結果如圖9所示， 由圖9a、圖9b、圖9c可知在第10 s施加電磁控制力后，轉子-軸承-AMA系統各測點振幅均得到抑制，說明了該算法的有效性，由圖9d可知經陷波濾波器濾波后噪聲現象得到明顯抑制。

圖9 各測點試驗結果Fig.9 Test results of each measuring point

轉速為1 950 r/min時1#測點y方向頻域瀑布圖如圖10所示：1)陷波濾波器對噪聲的濾波效果顯著,各頻段內噪聲明顯，雖然每個頻率下噪聲都不大，但累計之后對控制效果影響較大，這也是采用陷波濾波器的原因。2)在惡劣工作環境下轉子系統噪聲明顯，在第10 s施加控制后，振動一二倍頻成分得到抑制，說明該算法能有效抑制不平衡和不對中故障引起的振動。

圖10 1#測點y方向瀑布圖Fig.10 Waterfall diagram in y direction of1# measuring point

5 結論

針對轉子-軸承-AMA系統的不平衡-不對中耦合故障，設計了基于AMA的PD控制算法，建立控制系統仿真模型。在試驗中設計陷波濾波器，以振動的工頻和二倍頻成分作為耦合故障的靶向抑制目標，對轉子振動進行主動抑制試驗。根據仿真和試驗結果得出以下結論：

1)從時域和頻域控制結果來看，離散PD控制器對多自由度、多轉速運動轉子軸系的不平衡-不對中耦合振動有較好抑制效果。

2)針對靶向抑制所選用的離散PD控制器結構簡單，魯棒性較差，隨轉速增大，其振動抑制率可能會減小。

3)陷波濾波器能有效提取相應倍頻，抑制振動信號的噪聲，且可根據實時轉速改變陷波頻率，滿足多轉速運行的需求。