基于多模態(tài)信息融合的水下移動(dòng)目標(biāo)定位
劉樹東,梁婷蓉,王 燕,張 艷
(天津城建大學(xué) 計(jì)算機(jī)與信息工程學(xué)院,天津 300384)
0 引言
水下無線傳感器網(wǎng)絡(luò)(underwater wireless sensor networks, UWSNs)在海洋資源勘探、水下軍事監(jiān)視、海洋環(huán)境監(jiān)測、地震海嘯預(yù)警等領(lǐng)域具有廣泛的應(yīng)用。基于UWSNs的潛艇、水下無人潛航器等水下航行器可進(jìn)入目標(biāo)海域進(jìn)行偵測,此過程中它們的位置和速度信息發(fā)揮著重要作用。因此,對(duì)水下移動(dòng)目標(biāo)精準(zhǔn)定位的研究有著重要的作用及意義。
水下移動(dòng)目標(biāo)定位主要通過觀測量信息進(jìn)行定位。信息類型有到達(dá)時(shí)間(time of arrival,TOA)、到達(dá)時(shí)間差(time difference of arrival, TDOA)、到達(dá)角(angel of arrival, AOA)、到達(dá)頻率差(frequency difference of arrival, FDOA)、接收信號(hào)強(qiáng)度(received signal strength indicator, RSSI)等。但在一些復(fù)雜定位場景中,基于單個(gè)觀測量的單一模態(tài)信息無法滿足定位精度要求,所以很多學(xué)者研究通過融合不同模態(tài)類型觀測量信息定位以提高定位精度,主要有以下兩種:TDOA/FDOA和TDOA/AOA。理論上在具有相同傳感器數(shù)量時(shí),相比于2個(gè)觀測量雙模態(tài)信息融合的定位方式,3個(gè)觀測量多模態(tài)信息融合定位對(duì)移動(dòng)目標(biāo)位置和速度信息有更高的估計(jì)精度。
目前定位的主要挑戰(zhàn)為定位系統(tǒng)方程的非線性問題。研究者針對(duì)非線性位置方程提出泰勒算法,但此算法需要較準(zhǔn)確的初始值且收斂性不確定。為解決上述問題,文獻(xiàn)[9]提出基于兩步加權(quán)最小二乘(two-step weighted least squares,TSWLS)的TDOA/FDOA聯(lián)合定位的經(jīng)典定位算法。以 TSWLS為框架,文獻(xiàn)[10]在文獻(xiàn)[9]的基礎(chǔ)上考慮了傳感器位置誤差,并且與無傳感器位置誤差情況中的克拉美羅下界(cramer-rao lower bound,CRLB)比較;文獻(xiàn)[12]提出基于自適應(yīng)TDOA和AOA聯(lián)合定位算法,由于其TDOA觀測量方程在兩階段定位算法中的自適應(yīng)性,與文獻(xiàn)[13]中傳統(tǒng)TDOA/AOA聯(lián)合定位相比,定位精度有所提高,但是此方法只能估計(jì)移動(dòng)目標(biāo)的位置信息,無法估計(jì)其速度信息;另外,文獻(xiàn)[14]雖融合了TDOA/FDOA/AOA多模態(tài)信息定位,可以同時(shí)估計(jì)目標(biāo)位置及速度,但其與上述文獻(xiàn)相同,均為借助TSWLS框架,通過引入輔助參數(shù)將非線性系統(tǒng)方程轉(zhuǎn)換為偽線性方程求解目標(biāo)狀態(tài)。此類方法存在噪聲小時(shí)估計(jì)精度高,噪聲較大時(shí)估計(jì)精度低,適應(yīng)測量噪聲能力較差的問題。
針對(duì)上述問題,本文提出一種基于 TDOA/FDOA/AOA多模態(tài)信息融合的三步定位算法。為充分利用多模態(tài)信息,算法前兩步融合移動(dòng)目標(biāo)聲信號(hào)到達(dá)不同傳感器的時(shí)間差、頻移差及角度信息建立非線性位置方程組,通過經(jīng)典TSWLS估計(jì)移動(dòng)目標(biāo)狀態(tài)信息。為更好地求解非線性位置方程組,彌補(bǔ)TSWLS框架噪聲大時(shí)估計(jì)精度低的缺陷,算法第三步將定位問題轉(zhuǎn)換為最大似然問題,引入鯨魚優(yōu)化算法對(duì)移動(dòng)目標(biāo)的位置和速度信息進(jìn)行優(yōu)化。優(yōu)化過程中,算法第三步在前兩步的基礎(chǔ)上構(gòu)造目標(biāo)狀態(tài)的初始種群,且將固定種群范圍變?yōu)閯?dòng)態(tài);設(shè)計(jì)含有不同觀測量測量誤差方差倒數(shù)權(quán)重信息的種群適應(yīng)度函數(shù),增加尋找最優(yōu)目標(biāo)的可能性。仿真實(shí)驗(yàn)表明,本文所提算法在一定噪聲條件下可以達(dá)到 CRLB且能夠更好適應(yīng)測量噪聲。
1 定位模型
本文基于水下傳感網(wǎng)絡(luò)的定位模型如圖1所示。

圖1 定位模型






假設(shè)目標(biāo)輻射信號(hào)到達(dá)第+1個(gè)傳感器節(jié)點(diǎn)的方位角和俯仰角分別為θ和 φ(= 0,1, … ,?1),根據(jù)圖1中目標(biāo)與傳感器節(jié)點(diǎn)之間的位置關(guān)系,所測方位角和俯仰角可分別表示為



2 基于TDOA/FDOA/AOA多模態(tài)信息融合定位算法
本節(jié)具體給出基于TDOA/FDOA/AOA多模態(tài)信息融合定位算法的推導(dǎo)過程。該算法分為三步,前兩步遵循TSWLS框架求解定位問題;第三步將定位問題轉(zhuǎn)化為最大似然問題,實(shí)現(xiàn)位置及速度解的優(yōu)化。
2.1 第一步,加權(quán)最小二乘法




對(duì)式(5)求時(shí)間導(dǎo)數(shù),可將FDOA信息方程線性化,其結(jié)果為



將式(6)和式(8)整理成矩陣形式為



為零矩陣。
根據(jù)式(3)和式(4)可得,關(guān)于方位角和俯仰角的真實(shí)值公式可變形為

由文獻(xiàn)[12]及圖1中相應(yīng)的三角形關(guān)系,將式(11)變換為

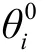




將式(15)和式(16)寫成矩陣形式為

結(jié)合式(9)和式(17),基于 TDOA/FDOA/AOA多模態(tài)信息融合的定位方程可以寫為

定位第一步的加權(quán)最小二乘解為

由于實(shí)際定位過程中,式(19)中的加權(quán)矩陣未知,所以先令=,得到移動(dòng)目標(biāo)估計(jì)值,然后利用初始估計(jì)值更新加權(quán)矩陣,從而得到更準(zhǔn)確的估計(jì)值。表達(dá)式為


2.2 第二步,考慮約束關(guān)系的加權(quán)最小二乘法



式(21)的加權(quán)最小二乘解為

式中:為第二步加權(quán)矩陣,若使的估計(jì)方差最小,其最優(yōu)選取為

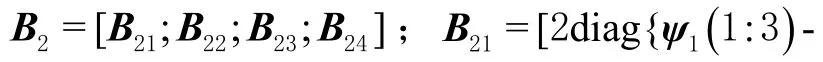
則第二步目標(biāo)位置和速度估計(jì)為

式中:=diag{sgin ((1 :3)-)}。
2.3 第三步,最大似然法
由于算法前兩步在求解非線性位置方程過程中,為增加可靠性加入TDOA、FDOA、AOA三個(gè)觀測量的測量誤差即噪聲項(xiàng),但此操作在噪聲較大時(shí),會(huì)嚴(yán)重影響算法的估計(jì)精度。所以算法第三步,利用最大似然法重新表述定位問題進(jìn)行求解,減少大噪聲對(duì)算法估計(jì)精度的影響。


式中,表示常數(shù)。移動(dòng)目標(biāo)位置和速度參數(shù)的似然函數(shù)可以表示為

因?yàn)槭剑?6)是非線性方程,無法得到解析解,所以本文采用改進(jìn)鯨魚優(yōu)化算法進(jìn)行求解。在實(shí)際定位中真實(shí)向量未知,所以用觀測量代替。為了提高本文定位算法在噪聲較大時(shí)的估計(jì)精度,增強(qiáng)算法適應(yīng)測量噪聲的能力,設(shè)計(jì)算法的適應(yīng)度函數(shù)為

式中:




當(dāng)<0.5時(shí),隨著值的減小,的變化范圍也在不斷縮小。當(dāng)?shù)闹翟趨^(qū)間[?1,1]上時(shí),通過減小當(dāng)前位置和目標(biāo)最優(yōu)位置之間的距離,從而靠近最優(yōu)目標(biāo)位置;當(dāng)?shù)闹挡辉趨^(qū)間[?1,1]上時(shí),隨機(jī)選擇一個(gè)位置,縮小隨機(jī)位置和當(dāng)前位置之間的距離更新,從而實(shí)現(xiàn)對(duì)搜索范圍的縮小。當(dāng)≥0.5時(shí),根據(jù)當(dāng)前位置和最優(yōu)位置之間的距離,在二者之間建立一個(gè)螺旋方程使當(dāng)前位置螺旋移動(dòng)更新。采用上述三種方式進(jìn)行位置更新,直到達(dá)到最大迭代次數(shù),則當(dāng)前最優(yōu)位置為最終目標(biāo)估計(jì)位置。
3 仿真實(shí)驗(yàn)
本節(jié)考慮兩個(gè)仿真場景,通過仿真實(shí)驗(yàn)評(píng)估本文算法的定位性能。場景1為使用6個(gè)傳感器節(jié)點(diǎn)對(duì)傳感器區(qū)域內(nèi)目標(biāo)進(jìn)行定位;場景2為使用6個(gè)傳感器節(jié)點(diǎn)對(duì)傳感器區(qū)域外目標(biāo)定位,兩個(gè)場景中傳感器節(jié)點(diǎn)均隨機(jī)分布在1 000 m×1 000 m×500 m的三維空間內(nèi)。上述兩個(gè)場景中的傳感器區(qū)域、目標(biāo)位置及其運(yùn)動(dòng)軌跡的二維平面示意圖如圖2所示,虛線框表示傳感器區(qū)域,6個(gè)傳感器節(jié)點(diǎn)隨機(jī)分布在傳感器區(qū)域內(nèi),場景 1中的目標(biāo)及其運(yùn)動(dòng)軌跡處于傳感器區(qū)域內(nèi),而場景 2中的目標(biāo)及其運(yùn)動(dòng)軌跡處于傳感器區(qū)域外。

圖2 定位場景二維平面示意圖



推導(dǎo)本文所提算法估計(jì)目標(biāo)誤差的CRLB為

式中:


3.1 目標(biāo)位于傳感器區(qū)域內(nèi)的仿真實(shí)驗(yàn)


圖3 目標(biāo)位于場景1時(shí)的位置RMSE曲線

圖4 目標(biāo)位于場景1時(shí)的速度RMSE曲線
圖5和圖6是本文算法及其對(duì)比算法估計(jì)位于傳感器區(qū)域內(nèi)目標(biāo)的 bias曲線。由圖5可知,當(dāng)總體測量誤差 1 0lg()≤10 dB 時(shí),就位置偏差而言,文獻(xiàn)[6]算法的表現(xiàn)要優(yōu)于其他算法,文獻(xiàn)[6]算法表現(xiàn)方差較高,偏差較低,這是由于該算法不同于其他算法,算法增加了牛頓迭代。圖5中當(dāng) 1 0lg()≤-10 dB時(shí),本文算法及對(duì)比算法的10lg(b ias)均小于0,即bias小于1m,所以相對(duì)于水下定位,不同算法估計(jì)位置的性能相差不大。當(dāng) 1 0lg()≥0時(shí),本文算法的偏差最小。由圖6實(shí)驗(yàn)結(jié)果可知,對(duì)傳感器區(qū)域內(nèi)的目標(biāo)進(jìn)行速度估計(jì)時(shí),本文算法估計(jì)偏差小于TSWLS算法。

圖5 目標(biāo)位于場景1時(shí)的位置bias曲線

圖6 目標(biāo)位于場景1時(shí)的速度bias曲線


圖7 目標(biāo)位于場景1時(shí)的位置估計(jì)CDF曲線

圖8 目標(biāo)位于場景1時(shí)的速度估計(jì)CDF曲線
3.2 目標(biāo)位于傳感器區(qū)域外的仿真實(shí)驗(yàn)


圖9 目標(biāo)位于場景2時(shí)的位置RMSE曲線

圖10 目標(biāo)位于場景1時(shí)的速度RMSE曲線
圖11和圖12是本文算法及其對(duì)比算法估計(jì)位于傳感器區(qū)域外目標(biāo)的bias曲線。由圖11可知,當(dāng)總體測量誤差 1 0lg()≤-30 d B 時(shí),本文算法及對(duì)比算法的10lg(bias)均小于0,即bias小于1 m。當(dāng) 1 0lg()>-10 d B時(shí),本文算法偏差最小,表現(xiàn)最優(yōu),文獻(xiàn)[6]算法次之,TSWLS最差。

圖11 目標(biāo)位于場景2時(shí)的位置bias曲線

圖12 目標(biāo)位于場景2時(shí)的速度bias曲線


圖13 目標(biāo)位于場景2時(shí)的位置估計(jì)CDF曲線

圖14 目標(biāo)位于場景2時(shí)的速度估計(jì)CDF曲線
3.3 傳感器節(jié)點(diǎn)數(shù)目對(duì)估計(jì)精度的影響


圖15 不同算法估計(jì)位置RMSE隨傳感器節(jié)點(diǎn)數(shù)變化情況

圖16 不同算法估計(jì)速度RMSE隨傳感器節(jié)點(diǎn)數(shù)變化情況
3.4 WOA算法、FDOA信息以及AOA信息對(duì)定位性能的影響
為了驗(yàn)證WOA算法、FDOA信息以及 AOA信息對(duì)定位性能的影響,在仿真場景 1中采用控制變量的思想,將本文所提算法與分別去除WOA算法、去除FDOA信息、去除AOA信息的算法相比較,本文算法及其去除不同信息后估計(jì)位置和速度的RMSE曲線如圖17和圖18所示。由圖17和圖18可知,本文算法要優(yōu)于去除WOA算法或任何一種觀測量信息的算法,這表明WOA算法及其他觀測量的加入對(duì)本文算法估計(jì)目標(biāo)位置及速度性能的提升具有積極作用。

圖17 本文算法及其去除不同信息后估計(jì)位置的RMSE曲線

圖18 本文算法及其去除不同信息后估計(jì)速度的RMSE曲線
本文算法及其去除不同信息后估計(jì)位置和速度的bias曲線,如圖19和圖20所示。由圖19可知,與去除任何一種觀測量信息或WOA的算法相比,本文算法估計(jì)位置的 bias曲線呈現(xiàn)出較大優(yōu)勢,本文算法的定位性能較好。由圖20可知,本文算法速度估計(jì) bias曲線不穩(wěn)定,在某些噪聲情況下估計(jì)速度的bias值要大于去除AOA信息和去除 WOA算法的 bias值。但是從縱坐標(biāo)軸的取值看,在10lg()小于等于0時(shí),三者之間的差距較小,小于1 m。總體上,由包含不同信息算法估計(jì)位置及速度的RMSE和bias曲線可知,本文算法要優(yōu)于分別去除WOA算法、去除FDOA信息、去除AOA信息的算法。

圖19 本文算法及其去除不同信息后估計(jì)位置的bias曲線

圖20 本文算法及其去除不同信息后估計(jì)速度的bias曲線
4 結(jié)束語
本文提出了一種基于 TDOA/FDOA/AOA多模態(tài)信息融合的三步定位法,該算法可以同時(shí)對(duì)移動(dòng)目標(biāo)位置及速度進(jìn)行估計(jì)。算法首先利用兩步加權(quán)最小二乘法獲得移動(dòng)目標(biāo)參數(shù)信息;然后通過推導(dǎo)將問題轉(zhuǎn)化為最大似然函數(shù)估計(jì)問題,引入鯨魚優(yōu)化算法,將包含目標(biāo)位置和速度的種群適應(yīng)度函數(shù)與測量噪聲方差相聯(lián)系,來提高估計(jì)精度。通過對(duì)傳感器區(qū)域內(nèi)外的移動(dòng)目標(biāo)仿真實(shí)驗(yàn)證明,本文算法相對(duì)于其他算法目標(biāo)參數(shù)估計(jì)精度高,且對(duì)系統(tǒng)測量噪聲具有良好的適應(yīng)能力。但是在實(shí)際情形中,由于海水的流動(dòng)性,傳感器會(huì)存在位置誤差,下一步將考慮傳感器位置誤差進(jìn)行仿真實(shí)驗(yàn)。

