基于深度學習模式下深度教學的設計與反思

李國林

[摘? 要] 促進深度學習要注重學生學習過程中的體驗、互動和生成性. 依托學生的基本活動經驗進行深度教學，設置問題情境，使經驗與知識相互轉化;教師因勢利導，指導學生深度地參與體驗，驅動學生思維深度發展;拓展探究對象，促進學生深度學習，以提升學生的研究興趣和學科素養.

[關鍵詞] 深度學習;深度教學;單調性

問題的提出

雖然課改已經十多年了，教師也在不斷地改進自己的教學方式，但是在教學中仍有很多困惑. 例如，教師用了同樣的講義和作業，學生似乎也能“照葫蘆畫瓢”，可是過一段時間后學生就表現出了不同的水平，差異越來越明顯.究其原因，其中很重要的一點是學生的學習是淺層次的，不能形成完整的知識體系，而教師又過分注重知識與技能，忽視了基本活動經驗，拘泥于“就課論課”，沒有深度教學，不能引導學生深度學習.《普通高中數學課程標準（2017年版）》提出，數學教學活動重心應從關注“教”轉到關注“學”. 教師要把教學活動的重心放在促進學生深度學習上.這就需要教師不斷更新觀念，對教學內容進行二次開發，多從事創造性活動，注重學生學習過程中的體驗、互動與生成性，形成邏輯連貫的思維體系.

學情分析

函數單調性是函數的重要性質，也是研究函數奇偶性及函數其他性質的“標尺”. 本節課是學生在學習了常用邏輯用語、函數的基本概念等知識后的內容，學生對新知識的研究有了一定的方法積累，所以本節課一開始用了大量的案例激發學生利用基本活動經驗“體會知識生成的過程”，抽象出函數單調性的概念;再通過探究“任意性”，使學生得到研究性質的一般框架，在活動中幫助每個學生最終獲得相對獨立的知識體系，為后期學習函數的其他性質提供新的活動經驗，培養學生數學抽象、邏輯推理、直觀想象、數學運算等數學核心素養.

教學片段

環節1：創設問題情境，喚起學生基本活動經驗，生成研究對象

情境1：生活中，在糖水中加糖，它會越來越甜，它反映了數學中哪些“量”變化的相互關系？

生1：隨著糖的增加，糖水越來越甜.

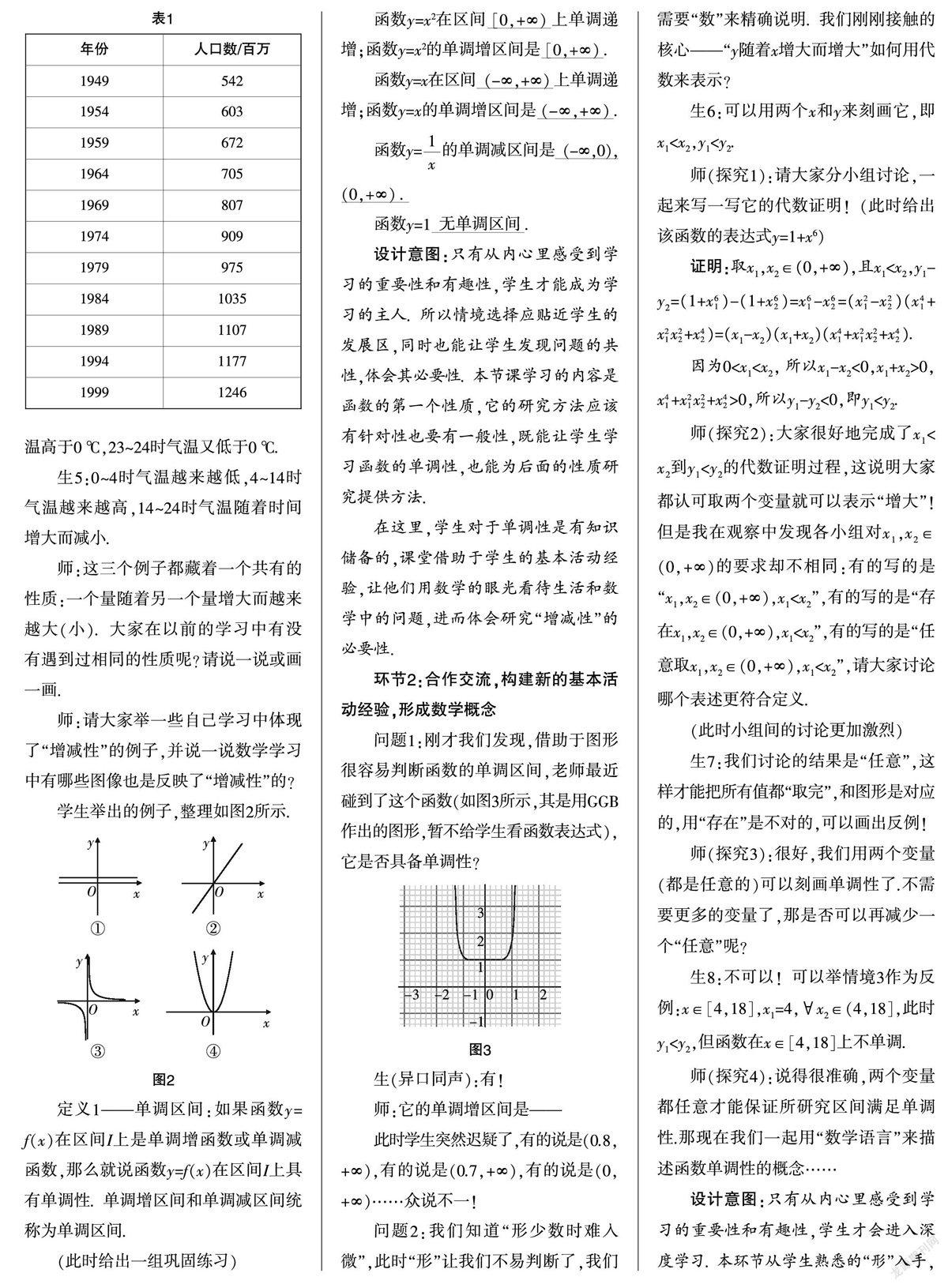
情境2：估計人口數量變化趨勢是我們制定一系列相關政策的依據，從人口統計年鑒中可以查得我國從1949年至1999年人口數據資料如表1所示，你能談談我國人口情況的變化規律嗎？

生2：我國人口隨著年份的增加而增加.

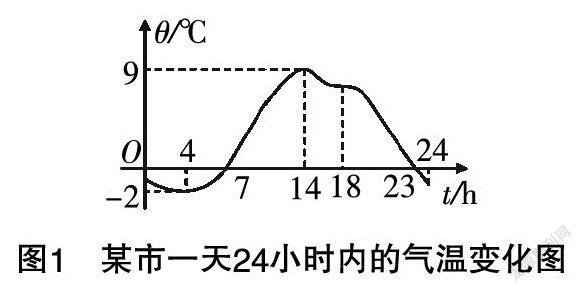
情境3：圖1是某市一天24小時內的氣溫變化圖，請你說出溫度與時間的關系.

圖1? 某市一天24小時內的氣溫變化圖

生3：t=4時氣溫最低，t=14時氣溫最高.

生4：0～7時氣溫低于0 ℃，8～23時氣溫高于0 ℃，23～24時氣溫又低于0 ℃.

生5：0～4時氣溫越來越低，4～14時氣溫越來越高，14～24時氣溫隨著時間增大而減小.

師：這三個例子都藏著一個共有的性質：一個量隨著另一個量增大而越來越大（小）. 大家在以前的學習中有沒有遇到過相同的性質呢？請說一說或畫一畫.

師：請大家舉一些自己學習中體現了“增減性”的例子，并說一說數學學習中有哪些圖像也是反映了“增減性”的？

學生舉出的例子，整理如圖2所示.

定義1——單調區間：如果函數y=f（x）在區間I上是單調增函數或單調減函數，那么就說函數y=f（x）在區間I上具有單調性.單調增區間和單調減區間統稱為單調區間.

（此時給出一組鞏固練習）

設計意圖：只有從內心里感受到學習的重要性和有趣性，學生才能成為學習的主人.所以情境選擇應貼近學生的發展區，同時也能讓學生發現問題的共性，體會其必要性. 本節課學習的內容是函數的第一個性質，它的研究方法應該有針對性也要有一般性，既能讓學生學習函數的單調性，也能為后面的性質研究提供方法.

在這里，學生對于單調性是有知識儲備的，課堂借助于學生的基本活動經驗，讓他們用數學的眼光看待生活和數學中的問題，進而體會研究“增減性”的必要性.

環節2：合作交流，構建新的基本活動經驗，形成數學概念

問題1：剛才我們發現，借助于圖形很容易判斷函數的單調區間，老師最近碰到了這個函數（如圖3所示，其是用GGB作出的圖形，暫不給學生看函數表達式），它是否具備單調性？

生（異口同聲）：有！

師：它的單調增區間是——

此時學生突然遲疑了，有的說是（0.8，+∞），有的說是（0.7，+∞），有的說是（0，+∞）……眾說不一！

問題2：我們知道“形少數時難入微”，此時“形”讓我們不易判斷了，我們需要“數”來精確說明. 我們剛剛接觸的核心——“y隨著x增大而增大”如何用代數來表示？

師（探究1）：請大家分小組討論，一起來寫一寫它的代數證明！（此時給出該函數的表達式y=1+x6）

（此時小組間的討論更加激烈）

生7：我們討論的結果是“任意”，這樣才能把所有值都“取完”，和圖形是對應的，用“存在”是不對的，可以畫出反例！

師（探究3）：很好，我們用兩個變量（都是任意的）可以刻畫單調性了.不需要更多的變量了，那是否可以再減少一個“任意”呢？

師（探究4）：說得很準確，兩個變量都任意才能保證所研究區間滿足單調性.那現在我們一起用“數學語言”來描述函數單調性的概念……

環節3：及時鞏固，借助于新的基本活動經驗進行數學應用

（1）質疑答辯，運用新知：討論下列說法的正確性.

說法1：若定義在R上的函數f（x）滿足f（2）>f（1），則函數f（x）是R上的增函數.

說法2：若定義在R上的函數f（x）滿足f（2）>f（1），則函數f（x）在R上不是減函數.

說法3：若定義在R上的函數f（x）在區間（-∞，0]上是增函數，在區間（0，+∞）上也是增函數，則函數f（x）在R上的增函數.

說法4：若定義在[0，+∞）上的函數f（x），對？坌x∈（0，+∞），都有f（x）>f（0），則函數f（x）在[0，+∞）上單調遞增.

（2）拓展探究，深化概念：剛剛大家列舉了一些初等函數（如圖2所示），各小組選擇一個函數，（合作）證明其在某個區間上的單調性.

設計意圖：通過環節1、環節2引導學生得到單調性的概念并告訴學生其是怎么來的、是什么，通過環節3中一組說法的判斷讓學生學會思考和應用，加深學生對單調性定義中“任意”的理解，推動學生到更高的知識層面上進行辨析和思考，促進學生深度學習.

環節4：歸納整理，融合新舊活動經驗，進行數學應用

師：通過本節課的學習，你有什么收獲？

從思想方法上看，學會了以形助數、以數解形，歸納類比，等等.

設計意圖：數學往往是這樣的：發現一個規律的過程需要有很高的智慧，但得出規律進行應用時，就顯得十分簡單了——那只是幾個有規律的思考步驟而已.因此課堂中重要的不僅是探究的結果，還有整個探究的過程.所以讓學生復盤反思，對整個課堂有一個整體的認識，加深概念的理解和掌握，達成深度學習的目的.

教學反思

1. 設置問題情境，經驗與知識相互轉化，打好深度學習的基礎

教育的意義不是教師將教材中的知識灌輸給學生，來到課堂的學生也不是一張白紙，他們是帶著經驗來的. 這些經驗可能是從日常生活中得來的，也可能是之前教師教授且內化為自己的，而問題情境的作用就是喚醒學生的已有經驗，因此在教學中需要教師創設、改造問題情境，使學生的經驗由片面變得全面、由復雜變為簡潔、由錯誤變為正確.本文執教者從學生經常接觸到的情境出發，喚醒學生的基本活動經驗，相互交流不同的經驗結果，生成共性的研究對象，從而激發其興趣、好奇心等深層次的學習動機.

2. 教師深度教學，指導學生深度體驗，驅動學生深度思維

學生學習的最終目的不是掌握已有的知識或技能，而是培養能靈活運用所學、適應發展需求的人才.因此教師在課堂上不能僅僅把知識“平移”給學生，而是要通過深度教學引導學生參與到教學活動中來，學生也必須以主動的、明辨是非的方式參與課堂.這種活動不是冷冰冰的思考，而是鮮活的、有溫度的交流. 問題是思維的起點，本節課根據學生對“增減性”已有的“讀圖”經驗，設計不容易“讀出”的圖形，與學生現有認知產生沖突，再引導學生用“數”“形”來完善活動經驗. 對于本節課的教學難點——“任意性”，用問題引導學生思考，將學生的思維引向深處，從而更好地理解概念.通過經歷單調性概念生成的過程，辨析“任意”和“存在”的區別，學生才能感同身受，體會數學先輩們凝練的智慧，體會教學內容對于個人精神成長的意義，提升他們的學科素養.

3. 本質與變式，深度研究對象，促進學生深度學習

深度學習不是盲目記憶，也不是“題海戰術”，而是通過教師的深度教學、主題活動把握知識的本質. 本節課讓學生感受三個問題情境的目的是讓其根據經驗提煉出“單調性”研究的必要性及它的初步特征，再通過活動體驗得到知識的本質. 而知識的本質又需要通過典型的例題、變式來把握，加工研究對象，在變式中完成本質的深度把握. 通過“及時鞏固”，讓學生辨析概念，讓學生從不同的角度加深對單調性的理解，完善知識體系. 這樣不僅能幫助學生站在一定高度認識單調性，也有助于學生將學習單調性所獲得的基本活動經驗類比到其他知識的學習上去. 這樣有利于學生思維的系統化，促進學生深度學習.

結束語

深度教學是一種建立在一定高度的教學設計，注重學生學習過程中的體驗、互動與生成性，形成邏輯連貫的思維體系. 這需要教師不斷更新觀念，對教學內容進行二次開發，多從事創造性活動研究，正如章建躍先生所說，“我們的教學應注重數學知識發生發展過程的合理性、學生思維過程的合理性”，這樣才可以引導學生深度學習.