有限轉角力矩電機設計及優化

周 力，唐 慶，譚慧萍，周探洲，王 欣，邱亞博，陳 輝

(1.中國航發貴州紅林航空動力控制科技有限公司，貴陽 550000；2.空軍裝備部駐成都地區軍事代表局駐貴陽地區第二軍事代表室，貴陽 550000；3.武漢理工大學 高性能船舶技術教育部重點實驗室，武漢 430063)

0 引 言

隨著稀土材料的開發利用和電機技術的發展，有限轉角力矩電機越來越受到相關學者的關注。在有限轉角力矩電機設計方面，文獻[1-3]設計了一種繞線式有限轉角電機，為實現線性的輸入-輸出關系，提出了一種閉環燃油控制算法，最終將其應用于柴油機調速器執行器和小型燃氣渦輪發動機。文獻 [4]設計一款有限轉角永磁無刷直流電機，并應用于導彈舵機及雷達的驅動機構上，該電機的最大驅動轉矩約為0.6 N·m。在爪極式有限轉角力矩電機設計方面，文獻[5]研制出一種取消了電換向器和滑環結構的混合勵磁爪極電機，將等效磁路法與有限元仿真相結合，對電機結構進行了優化，顯著提高了電機的輸出效率。文獻[6]對無刷爪極雙轉子電機轉矩性能影響因素進行了分析，提出了改善電機功率因數的方法，研制了無刷爪極雙轉子電機的實驗樣機，進行了性能試驗。

有限轉角力矩電機根據電機定子結構分為齒槽式結構和無齒槽式結構，齒槽式電機產生的齒槽轉矩會導致電機在運行轉角范圍內的工作轉矩產生較大波動。相比之下，無齒槽式有限轉角電機將環形線圈直接繞制在定子鐵心上，從結構上避免了齒槽效應的產生，可在相對較大的運行區間具有相對穩定的力矩性能，但無齒槽式電機存在等效氣隙大和力矩密度低等問題。

本文提出了一種爪極式有限轉角電機拓撲結構，采用整體式轉子磁軛、無齒槽定子爪極結構。基于等效磁路法建立了爪極式有限轉角電機的等效磁路模型，推導出了爪極式有限轉角電機電磁轉矩解析式，采用Maxwell軟件對電機的尺寸參數和材料屬性進行校準，并對電機空載特性進行分析，驗證設計方案的合理性；根據結構參數對空載反電動勢和磁阻轉矩的影響規律，建立電機優化模型，并對電機優化變量及相關約束條件進行了選取，利用電機優化設計模塊中的遺傳算法對目標函數進行了優化，得到了電機永磁體極弧系數、定子爪極寬度、氣隙長度、永磁體厚度等參數的最佳值。

1 爪極式有限轉角力矩電機結構設計

根據驅動執行機構控制性能要求，本文提出了一種爪極式有限轉角電機力矩設計方案，結合解析法和有限元分析[7]確定了電機的結構尺寸和材料屬性，完成了爪極式有限轉角力矩電機的初步設計。

1.1 船用柴油機調速器驅動機構性能要求

本文所設計的有限轉角力矩電機性能指標：電機外形尺寸，外徑D1≤112 mm，軸中心高≤85 mm；電機電磁轉矩范圍0.5～1.2 N·m；電機有限轉角范圍6°～85°。

1.2 電機拓撲結構

爪極式有限轉角電機拓撲結構如圖1所示。

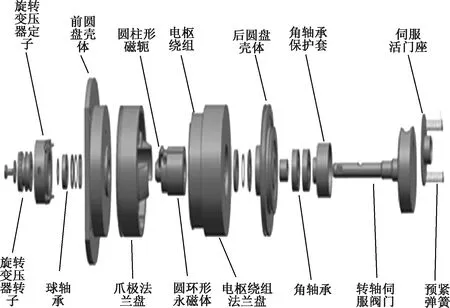
圖1 爪極式有限轉角電機拓撲結構圖

爪極式有限轉角電機主要由定子爪極和轉子磁軛組成。電機整體三維結構圖如圖2所示。

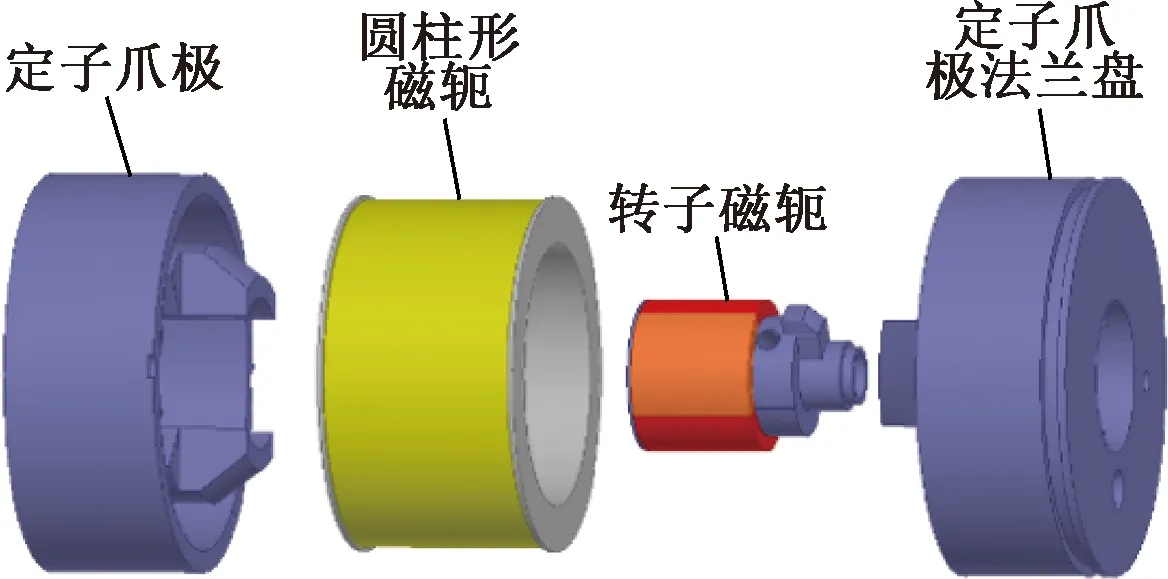
圖2 爪極式有限轉角電機三維結構圖

圖2中，電機轉子組件采用整體式轉子磁軛結構，由圓柱形磁軛、4塊永磁體、轉軸伺服閥門和緊固銷組成。電機定子采用無磁槽定子爪極結構，由單相線圈繞組、線圈繞組支架、鑲嵌襯圈的左右兩塊軸向四階梯形爪極法蘭盤和緊固螺釘構成；圓柱形不導磁骨架和單相電樞繞組嵌套在定子法蘭盤中；定子爪極法蘭盤設計有一定的限位角度，當電機轉動到對應角度時，便對電機轉子進行機械限位。

1.3 磁路機理分析

爪極式有限轉角電機磁路方向如圖3所示，稀土永磁體直接表貼在電機內轉子外表面上，形成固定徑向磁場，電樞繞組安裝在電機外定子的兩個四階梯形爪極法蘭盤中，通電后電樞繞組在不導磁線圈骨架作用下，產生的軸向磁通，通過四階梯形爪極轉換為徑向磁通后，它與稀土永磁體形成的固定磁場相互作用，形成閉合磁通回路；從而產生有限轉角電磁轉矩，直接驅動電機做快速有限轉角運動。

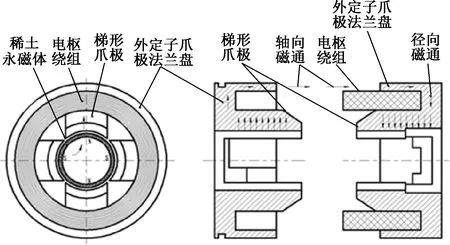
圖3 有限轉角力矩電機磁路圖

1.4 電機電磁轉矩解析推導

1.4.1 等效磁路模型建立

電機等效磁路模型[8]假設與簡化如下：

1)電機磁路是線性，忽略定子爪極處磁通邊緣效應以及飽和效應；

2)定子爪極法蘭盤與轉子磁軛材料磁導率為無窮大，忽略磁路中導磁材料部分磁壓降；

3)忽略電機內部渦流效應和磁滯損耗；

4)忽略爪極間的漏磁與端部漏磁。

根據電機的主磁通路徑，把爪極式有限轉角電機主磁路分別等效成含有磁阻與磁動勢的各個支路，由此建立電機等效磁路模型如圖4所示。

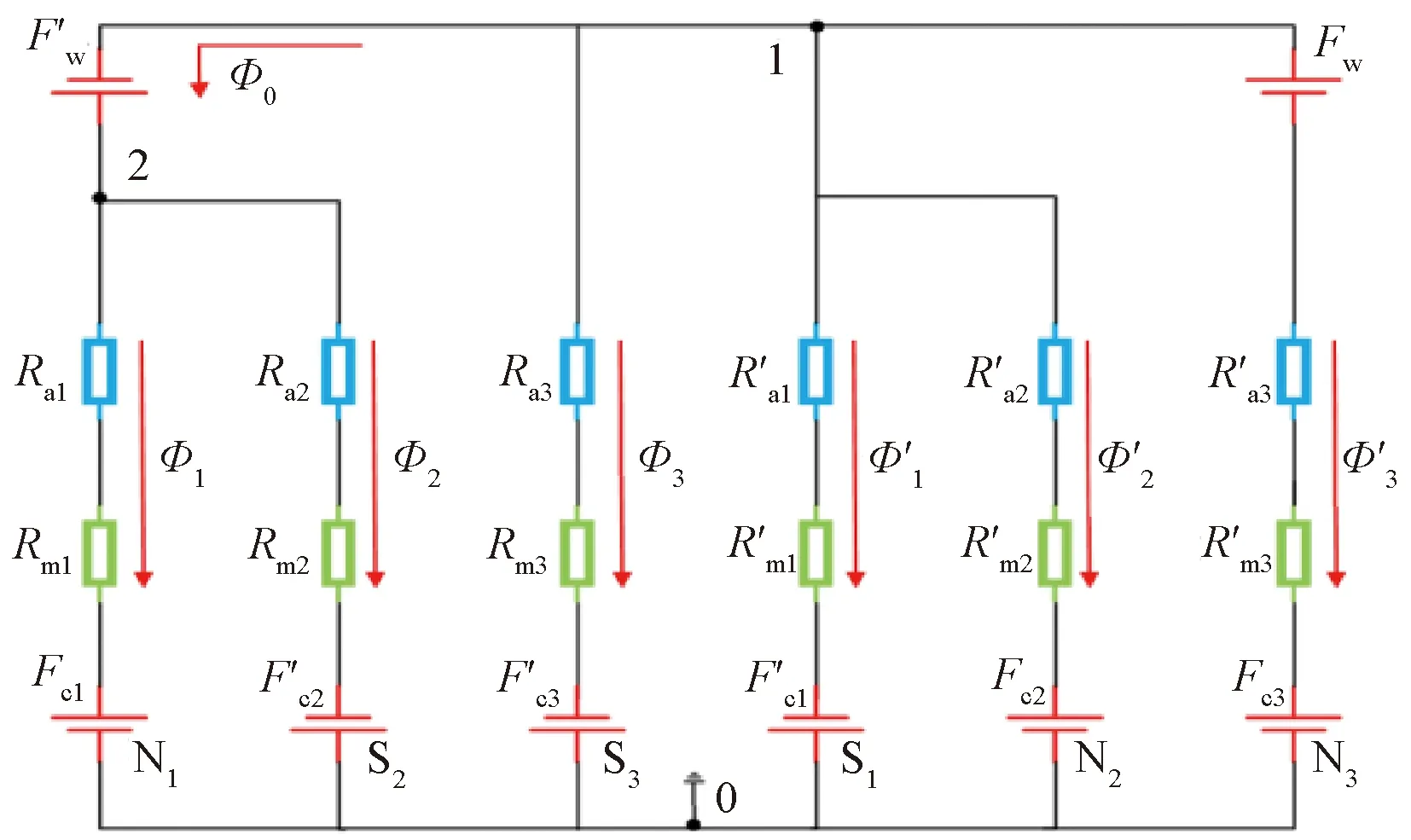
圖4 等效磁路模型圖

根據磁路與電路在數學上的相似性，利用電路中的節點電壓法分別求得圖4中各部分支路的磁壓降和磁通密度。磁路中各個部分的氣隙磁阻和永磁體磁阻都是轉子位置角θ的函數，永磁體磁動勢和繞組磁動勢的表達式[9]：

Fc1=Fc2=Fc3=F′c1=F′c2=F′c3=HchM

(1)

Fw=F′w=NcI

(2)

式中：Hc是永磁體矯頑力；hM是永磁體厚度；Nc是線圈繞組匝數；I是電機線圈電流。

得到節點磁動勢Fn1，Fn2表達式如下：

(3)

Fn2=Fn1+Fw

(4)

1.4.2 電磁轉矩推導

根據所求得的節點磁動勢，可求出磁路模型中流過永磁體與氣隙處的各支路的磁通大小，表達式如下：

(5)

(6)

(7)

(8)

(9)

(10)

當磁路為線性磁路時，氣隙與永磁體處的磁共能表達式：

(11)

最終的電磁轉矩解析式：

(12)

式中：p是極對數；μ0是空氣磁導率；μr是永磁體材料的相對磁導率；Lef是電機軸向有效長度；r1、r2、r3分別是轉子上的永磁體內半徑、外半徑以及定子爪極內半徑。

根據電磁轉矩表達式(12)，電機電磁轉矩除受電機極對數、繞組電流安匝數、永磁體相對磁導率、矯頑力等電磁屬性影響外，還與電機軸向有效長度、永磁體厚度、電機爪極以及永磁體結構參數相關。利用式(12)即可對爪極式有限轉角電機的初始尺寸及電磁參數進行設計。

2 電機結構尺寸和材料屬性設計

2.1 電磁負荷設計

電機單相繞組導通時，電機磁負荷的表達式：

(13)

式中：φ是定子爪極每極的主磁通；τ是轉子上的永磁體極距；Lδ是電樞計算長度。

電機電負荷的表達式：

(14)

式中：Nz是單相定子繞組匝數；D2是定子爪極外徑；I是單相繞組電流。

普通有限轉角力矩電機，Bδ在0.4～1.2 T之間取值；A在150～800 A/m之間取值。

2.2 電機基本尺寸和材料屬性設計

爪極式有限轉角電機的主要結構尺寸包括定子爪極內徑、爪極外徑、轉子磁軛外徑、永磁體內外徑、電機軸向有效長度和氣隙長度。

1)主要尺寸比

電機主要尺寸比為電機軸向有效長度與定子法蘭盤外徑的比值，對于表貼式永磁電機，一般的取值范圍為0.4～1.5。

2)氣隙長度

氣隙長度δ是電機設計過程中的一個重要參數[10]，氣隙長度估算公式如下：

(15)

式中：D3是定子爪極內徑。

3)永磁體尺寸

永磁體尺寸設計包括永磁體磁化方向厚度、永磁體寬度和永磁體軸向長度。永磁體磁化方向厚度和永磁體寬度預估公式如下：

(16)

bM=αpτ

(17)

式中：μr是永磁體材料的相對磁導率；Br是永磁體材料的剩磁密度；Bδ是平均氣隙磁密，Br/Bδ取在1.1～1.35之間；δi是計算氣隙長度；αp是永磁體極弧系數。

4)單相線圈繞組匝數

電樞繞組的線圈匝數計算公式：

(18)

式中：E0是空載感應電動勢；KW是電機繞組系數，對于環形繞組來說繞組系數取1；KB是磁場波形系數；N是單相繞組匝數。

式(18)中感應電動勢頻率f的計算公式:

(19)

式中：n是電機轉子轉速；p是電機轉子上永磁體極對數。

結合電機電磁負荷、定子爪極尺寸和式(14)，確定線圈繞組匝數為180匝。

5)電機各結構材料選擇

電機基本結構參數如表1所示，電機的材料屬性如表2所示。

表1 電機結構參數

表2 電機材料屬性

選取材料為SmCo30、矯頑力為800 kA/m、剩磁為1.09 T的釤鈷永磁體；線圈結構采用漆包線、環形平繞；電機用來嵌放線圈的圓柱形不導磁骨架，采用樹脂絕緣不導磁材料；電機定子爪極法蘭盤及轉子磁軛部分設計采用導磁性較好的10#鋼材料鑄造而成。

2.3 有限元分析驗證

采用Maxwell軟件對電機進行磁場分布和矩角特性分析。

1)磁通路徑分析驗證

轉子磁軛中心線與定子爪極中心線位置重合時的電機磁通密度矢量分布圖如圖5所示。在此位置電機主磁路的磁阻最小，由永磁體產生的勵磁磁通經過氣隙與定子爪極形成閉合回路，經過定子法蘭盤軛部鏈過電樞繞組的主磁通最大。可以觀察到電機內磁場存在著徑向磁通和軸向磁通，其中只有經過定子爪極法蘭盤軛部的軸向磁通才是產生感應電動勢的有效磁通。

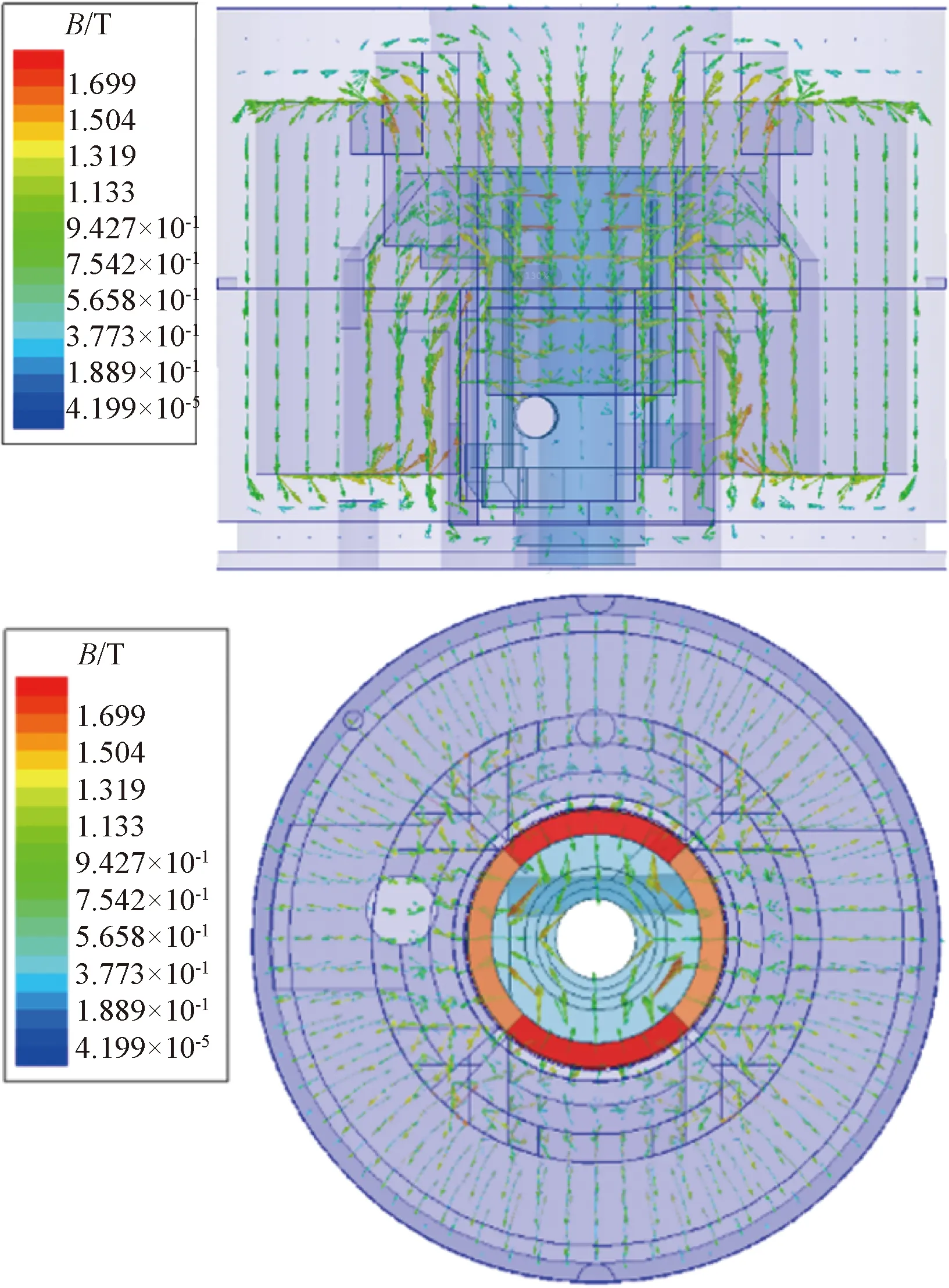
圖5 爪極式有限轉角電機磁通密度矢量分布

2)矩角特性分析驗證

在單相繞組通入3 A直流電時產生的矩角特性曲線如圖6所示，電磁轉矩在控制性能要求范圍內，且磁阻轉矩數值大小所占電磁轉矩的比例符合爪極式有限轉角電機力矩的設計特點。

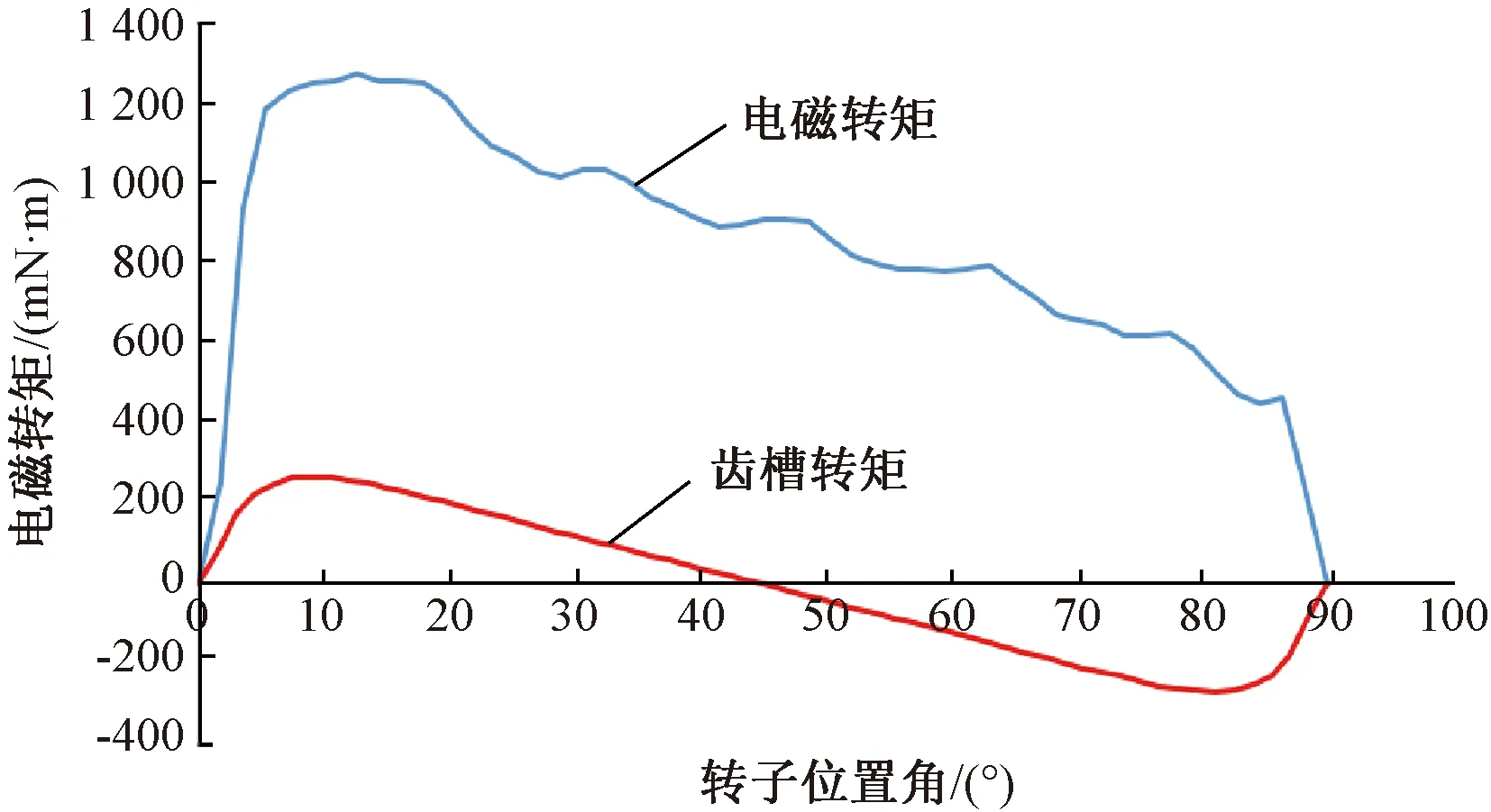
圖6 爪極式有限轉角電機矩角特性

3 轉矩性能分析

電機轉矩波動受磁阻轉矩和反電動勢畸變率兩方面影響。首先推導出磁阻轉矩及反電動勢畸變率的解析表達式，分析結構參數對電機反電動勢波形以及磁阻轉矩的影響；然后通過多目標遺傳算法對結構參數優化，得到了反電動勢波形畸變以及磁阻轉矩綜合性能最優時的電機結構。

3.1 磁阻轉矩及反電動勢畸變率解析

電機為4極4爪極結構，電機運行時在爪極與爪極之間會產生類似于齒槽的作用，由于電機轉子上的永磁體極數與定子爪極數相等，故有限轉角電機的一個電磁轉矩周期內只有單個周期的磁阻轉矩。假設定子爪極法蘭盤以及轉子磁軛部分的磁導率視為無窮大，設電機斷電時磁場能量為W，取定子爪極中心線位置時的位置角θ為0，取轉子磁軛中心線與定子爪極中心線的夾角為相對位置角α，此時磁阻轉矩可表示如下：

(20)

由式(20)可知，磁阻轉矩與電機內的磁場儲能隨位置角的變化規律相關。而電機內磁場儲能主要是由永磁體中所儲存的磁場能量和氣隙中所儲存的磁場能量兩部分組成[16]，則電機內的磁場儲能可近似表示為：

(21)

式中：Wpm是永磁體內磁場能量；Wair是氣隙內的磁場能量；μ0是真空磁導率；B(θ,α)是氣隙磁密圓周分布。

B(θ,α)可表示如下：

(22)

式中：Br(θ)為永磁體剩磁；δ(θ,α)為有效氣隙長度圓周分布；hM(θ)為永磁體充磁方向長度。

隨著電機的旋轉，轉子位置角發生變化，永磁體內磁場能量基本不變，因此磁阻轉矩與氣隙磁場能量的變化緊密相關。此時的磁共能：

(23)

(24)

(25)

最終得到磁阻轉矩表達式：

(26)

式中：La是定子法蘭盤爪極部分軸向長度；p是永磁體極對數；R1、R2分別是永磁體外半徑、定子爪極內半徑；Ns是電機定子爪極數；αp為永磁體極弧系數；n為使得nz/(2p)為整的整數。

反電動勢波形畸變率的表達式：

(27)

式中：U1為空載反電動勢基波有效值；Uk為空載反電動勢k次諧波的有效值。

3.2 結構參數對轉矩性能的影響

3.2.1 磁體極弧系數的影響

永磁體極弧系數指的是永磁體極弧寬βp和永磁體極距τ的比值。在電機其他結構參數保持不變的基礎上，在0.7～1范圍內改變永磁體極弧系數αp的取值，得到的電機轉矩性能曲線如圖7所示。

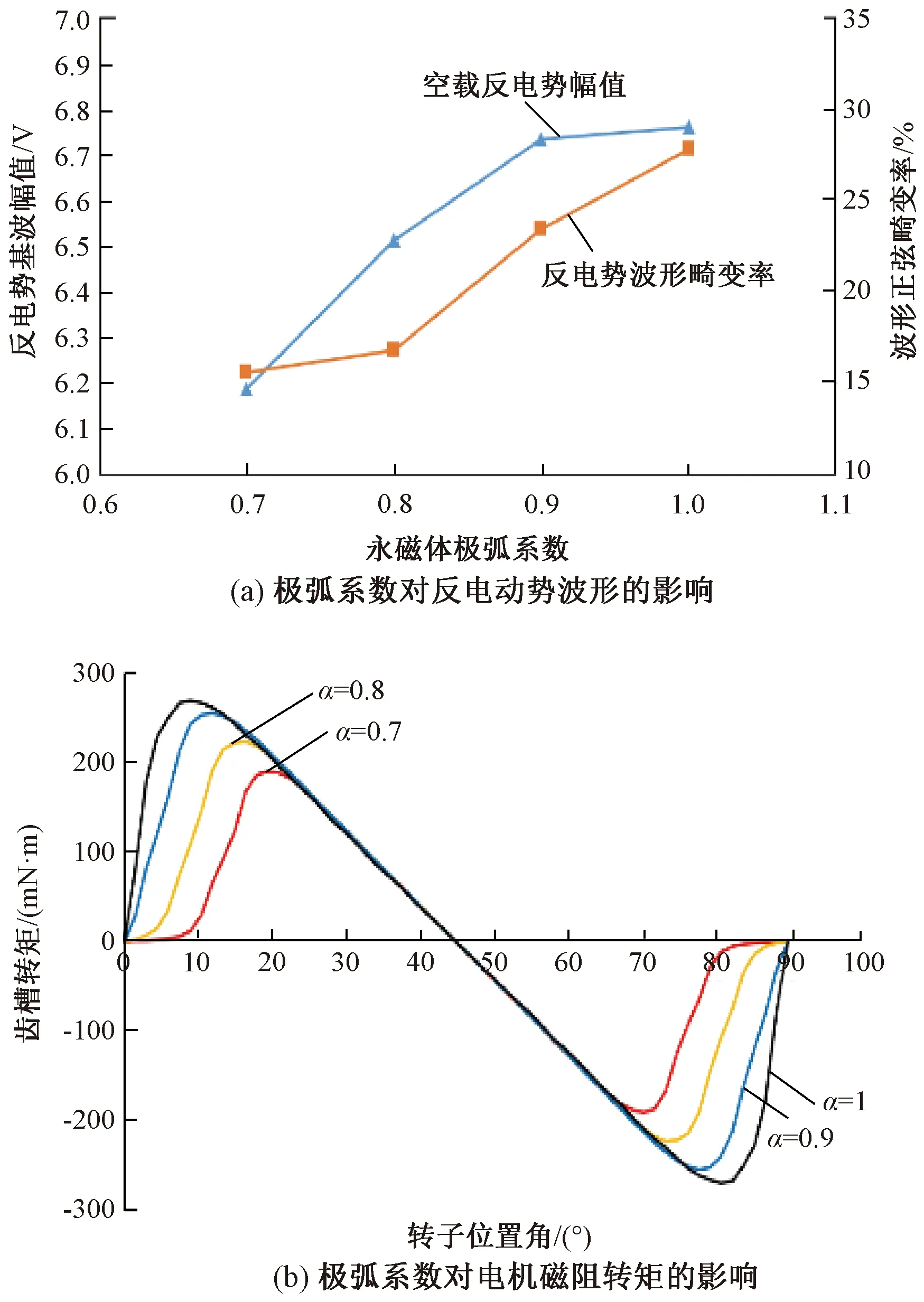
圖7 永磁體極弧系數對電機特性的影響

從圖7(a)可以看出，反電動勢幅值和波形畸變率隨極弧系數的增大而增大，單增長趨勢會逐漸變緩，可考慮降低極弧系數改善反電動勢波形。此外，永磁體極弧系數電機在6°～85°轉角范圍內受轉矩大小限制，不能過小。由圖7(b)可知，極弧增大時電機的磁阻轉矩亦會隨之增大，且峰值對應角度亦會隨之提前。

3.2.2 定子爪極寬度對轉矩性能的影響

改變定子爪極寬度，會引起相鄰爪極間氣隙磁導的變化進而影響電機的轉矩性能。在定子齒寬22 mm～28 mm的范圍內，定子爪極寬度對轉矩性能的影響如圖8所示。

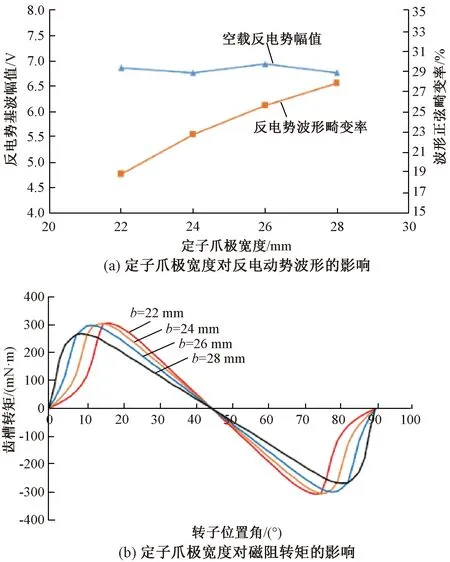
圖8 定子爪極寬度對電機特性的影響

從圖8(a)中可知，爪極寬度對反電動勢基波幅值影響較小，維持在6.7 V左右浮動。反電動勢波形畸變率隨爪極寬度的增加而上升，從反電動勢諧波含量考慮，爪極寬度應越小越好。由圖8(b)可知，磁阻轉矩峰值隨著爪極寬度的增加而提前出現，且峰值、谷值亦會隨著爪寬的增加而降低。因此電機磁阻轉矩會伴隨著爪極寬度的增加而減小，在爪極寬為28 mm時達到最小。

3.2.3 氣隙長度對轉矩性能的影響

氣隙長度的變化對轉矩性能影響如圖9所示。

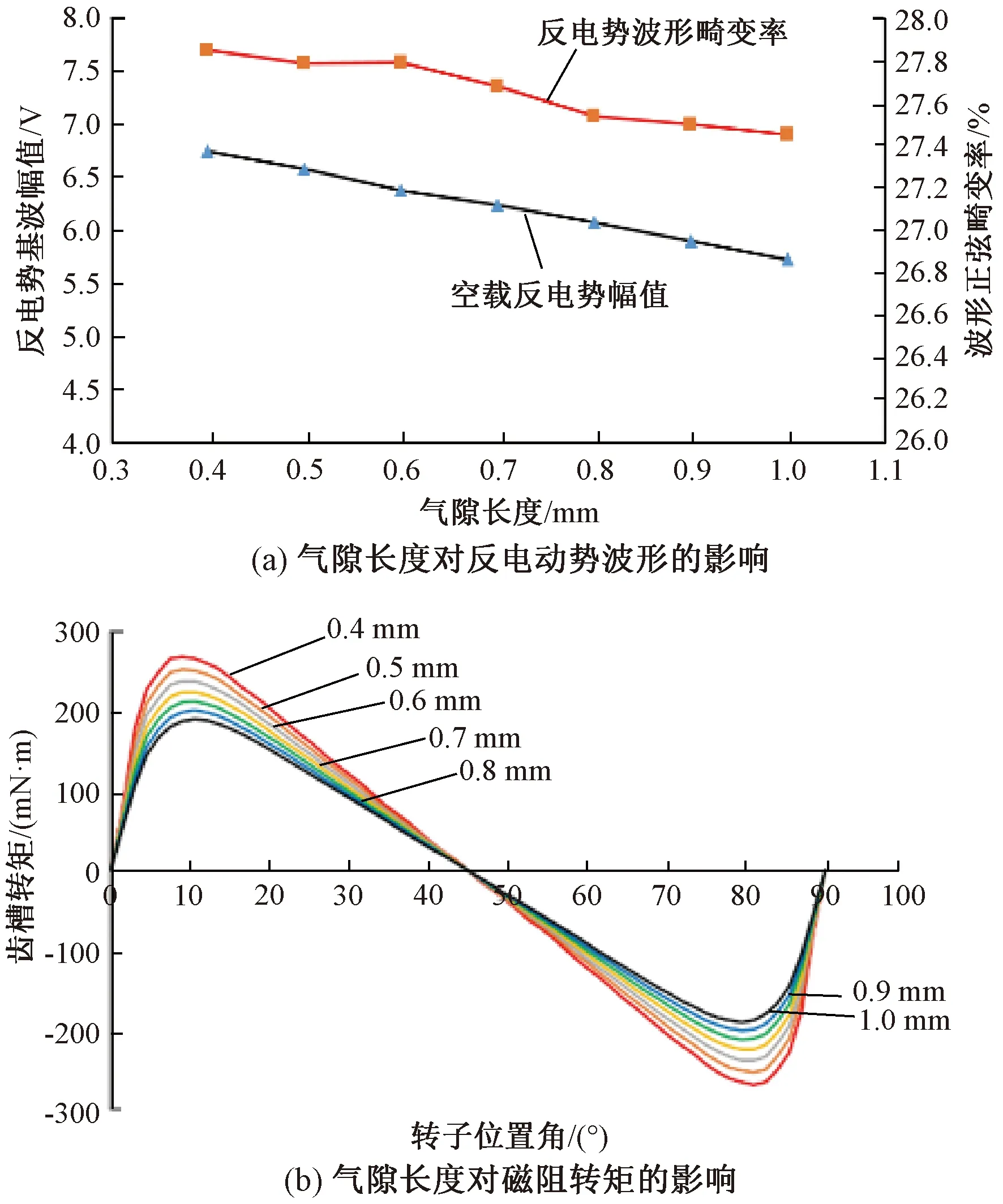
圖9 氣隙長度對電機特性的影響

圖9(a)展示了氣隙長度對磁阻轉矩的影響；從圖可知，對爪極式有限轉角電機來說，氣隙越小，電機的電磁轉矩就越大；但同時電機的磁阻轉矩也會隨之越大。從圖9(b)中可知，隨著氣隙長度的增加，電機的空載反電動勢幅值隨之降低，反電動勢波形畸變率也隨之下降但趨勢并不明顯，基本維持在26%左右浮動。

3.2.4 永磁體厚度對轉矩性能的影響

爪極式有限轉角電機定子內徑為41.5 mm，電機單邊氣隙取為0.35 mm，轉子外徑分別為34.8 mm、32.8 mm、30.8 mm、28.8 mm，永磁體厚度分別取3 mm、4 mm、5 mm、6 mm，保持電機其他結構參數不變進而分析電機轉矩特性。永磁體厚度對轉矩性能的影響如圖10所示。

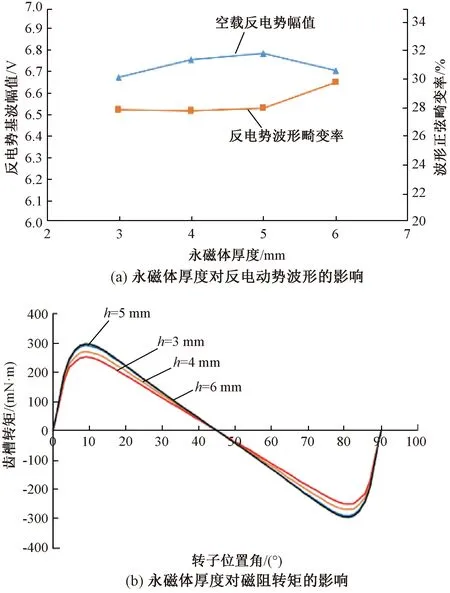
圖10 永磁體厚度對電機特性的影響

由圖10(a)可知，反電動勢基波幅值在6.7～6.8 V之間，波形畸變率在28%左右，當永磁體厚度為6 mm時上升到30%，雖然有一定的波動，但總體上受永磁體厚度的影響不大。由圖10(b)可知，永磁體厚度對轉矩性能有一定的影響，磁阻轉矩隨永磁體厚度的增加而增大，但增加的趨勢逐漸減緩，直至6 mm時基本不再發生變化。

4 基于多目標遺傳算法的轉矩優化

4.1 多目標遺傳算法

采用精英策略的非支配排序遺傳算法(elitist non-dominated sorting genetic algorithm，以下簡稱NSGA-II)為本文多目標優化算法，NSGA-II的核心就是協調各個目標函數之間的關系，找出使得各個目標函數都盡可能達到比較理想函數值的最優解集。

4.2 選取目標函數

選取磁阻轉矩幅值Tre、反電動勢波形畸變率Ku為分目標函數。優化目標為在0～90°的轉角范圍內，尋求針對電機磁阻轉矩幅值與反電動勢波形畸變率問題的整體最優解。

根據本文所選的兩個分目標函數，可得最終目標函數：

F(x)=ω1Tre+ω2Ku

(28)

式中：Tre是磁阻轉矩幅值；Ku是反電動勢波形畸變率。

4.3 確定設計變量及約束條件

由于電機主體結構尺寸已定，只對部分重要結構參數進行參數化分析優化，分析參數變量對磁阻轉矩和反電動勢波形的影響，選取永磁體極弧系數apr、定子爪極寬度b、永磁體厚度hM以及氣隙長度δ作為設計變量。根據設計變量對電機性能影響，確定了各設計變量取值范圍，如表3所示。

表3 優化變量及取值范圍

根據電機性能的要求，為了保證電機在6°～85°轉角范圍內，電磁轉矩滿足在0.5～1.2 N·m之間，要求電磁轉矩的約束范圍：

0.5 N·m≤g1(x)≤1.2 N·m

(29)

轉角約束范圍：

6°≤g2(x)≤85°

(30)

4.4 優化結果分析

目標函數與迭代次數變化關系如圖11所示。

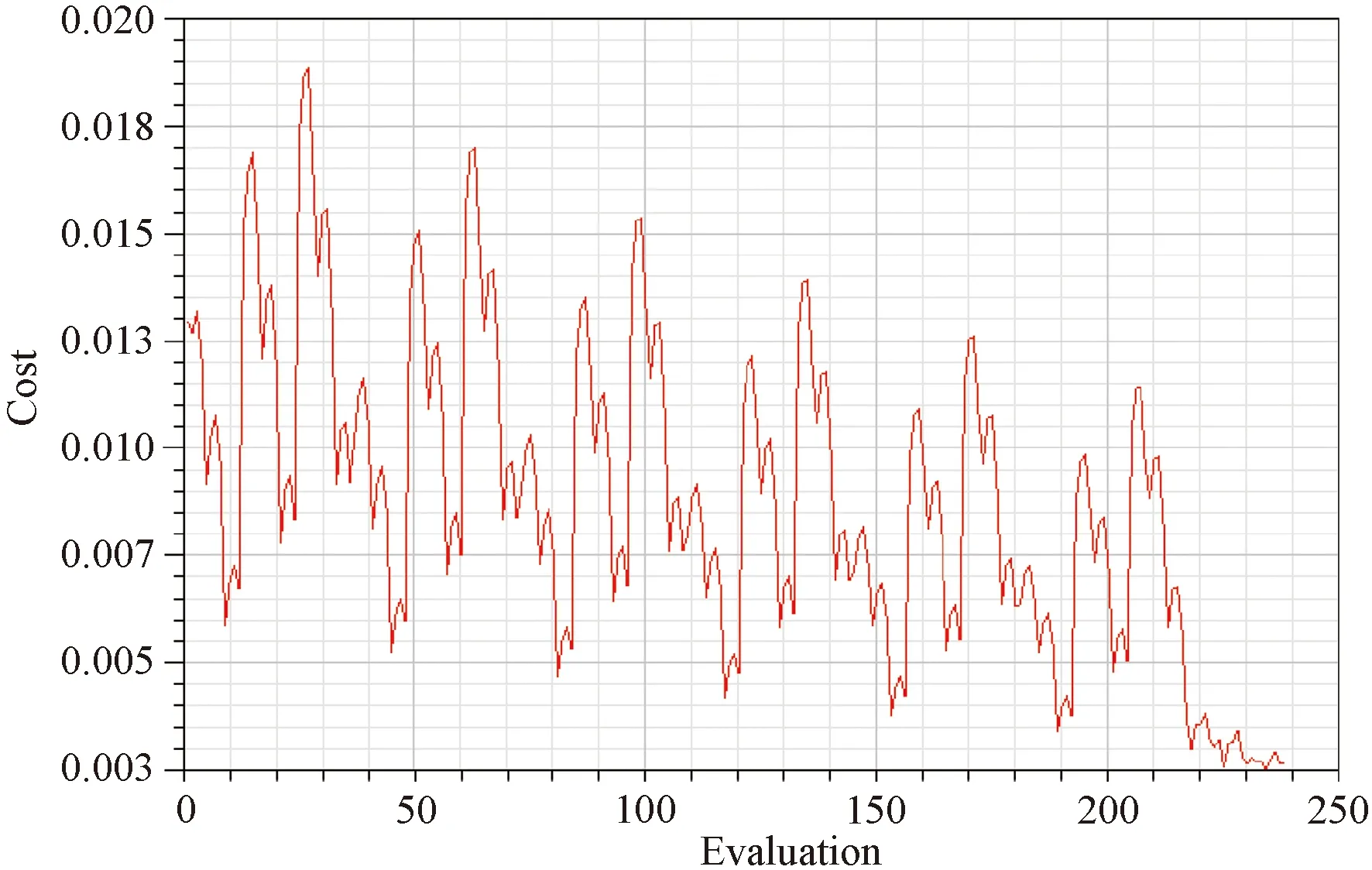
圖11 目標函數與迭代次數變化關系圖

表4列出了優化前后的結構參數變量。

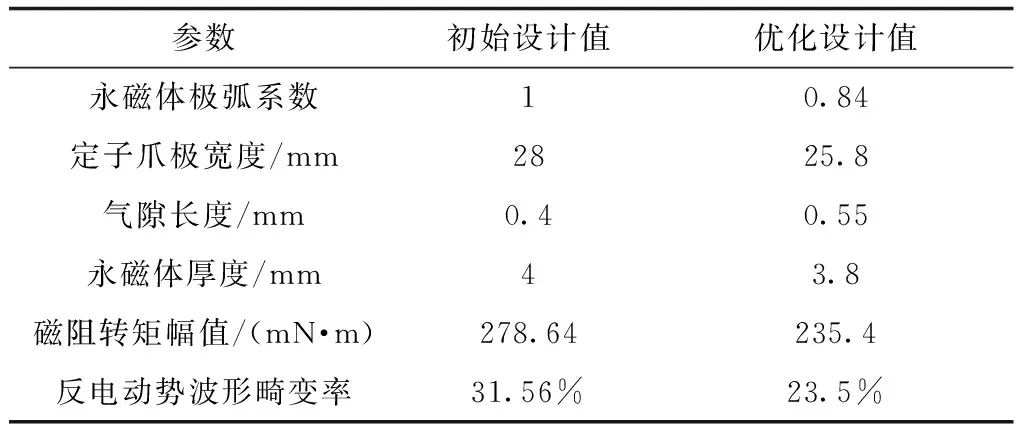
表4 優化前后參數變量

參數未優化電機的空載反電動勢諧波分析結果如圖12所示。優化后的電機磁阻轉矩波形對比如圖13所示。

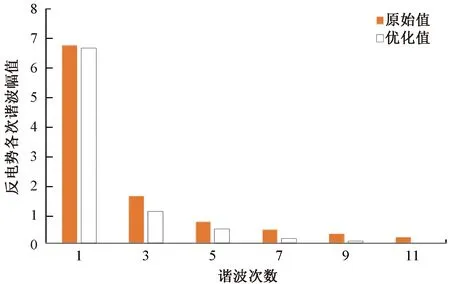
圖12 優化前后的空載反電動勢諧波含量對比

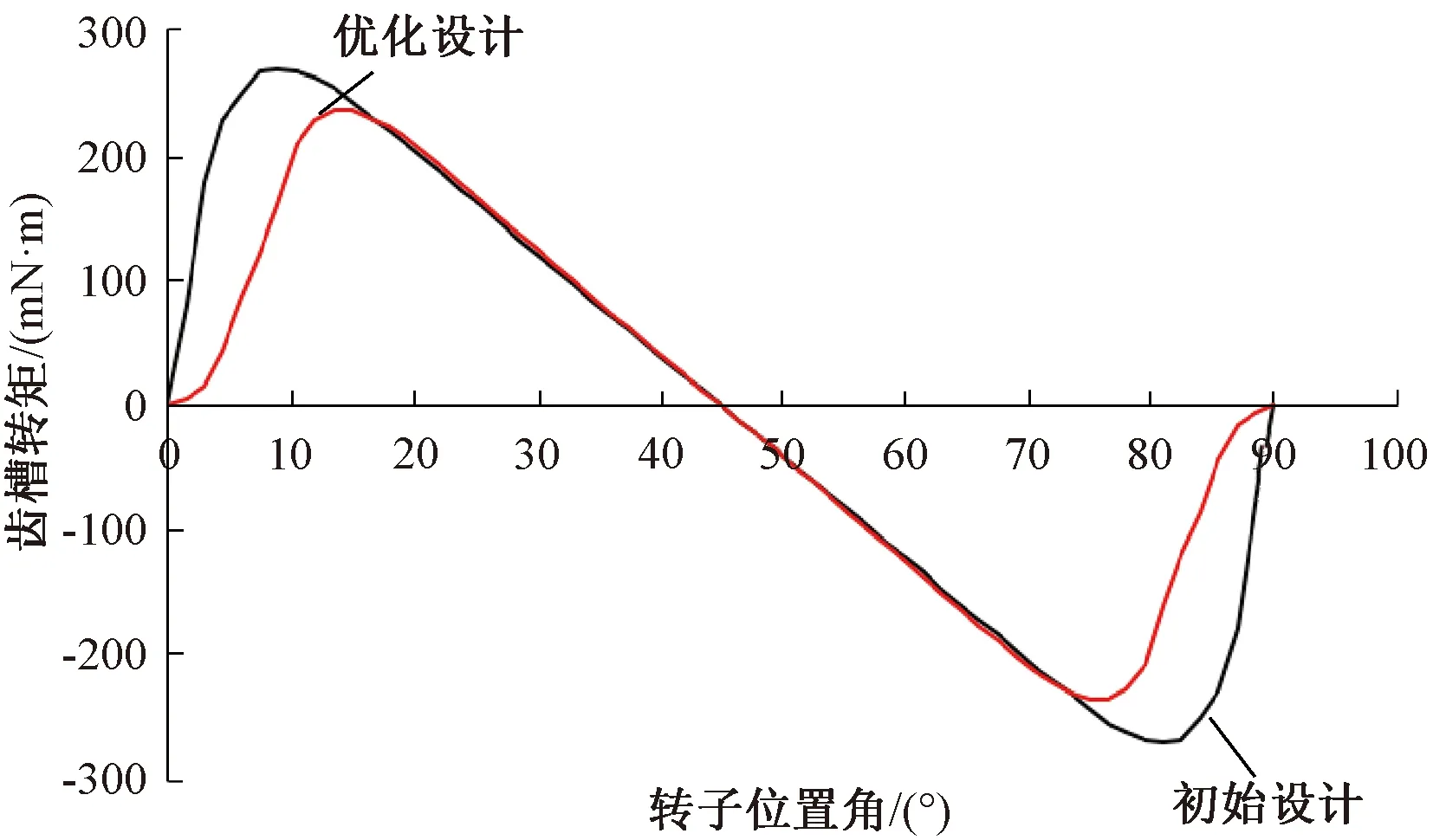
圖13 優化前后的磁阻轉矩對比

從圖12優化后的諧波含量可知，空載反電動勢波形畸變率約為23.5%，相對于初始設計的31.56%，電機反電動勢波形有了較大程度改善。由圖13可看出，優化后的電機磁阻轉矩幅值為235.4 mN·m，相比于初始設計值278.64 mN·m，降低了15.51%；在電機[15°, 75°]轉角區間內，電機磁阻轉矩波形基本一致。即在運行區間內，電磁轉矩只受到磁阻轉矩幅值的影響較大。參數優化前后電機在一個轉矩周期內的波形對比如圖14所示。

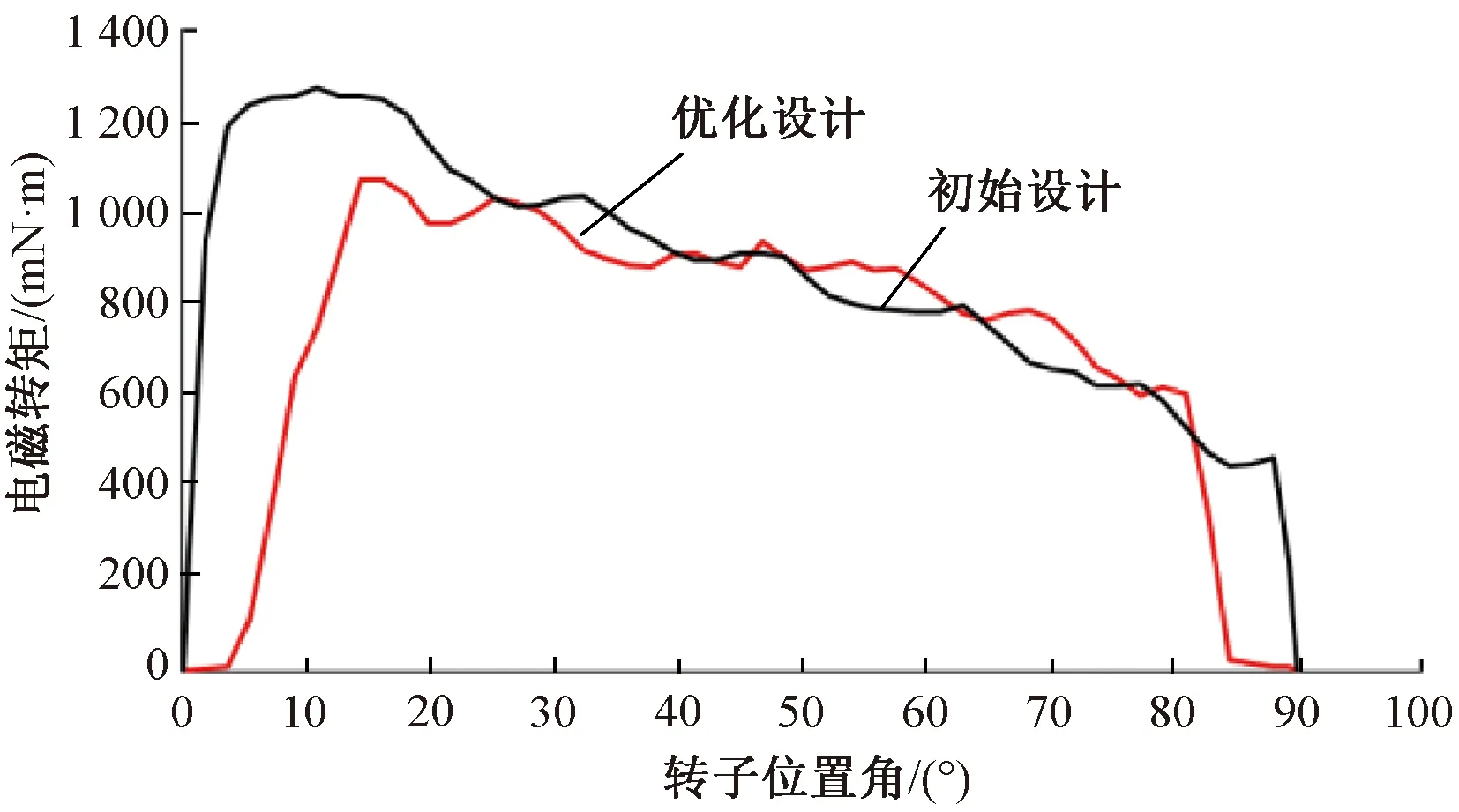
圖14 優化前后的電磁轉矩對比

從圖14可知，優化后的電磁轉矩在有限轉角范圍內的轉矩最大值約為1.05 N·m，最小值約為0.62 N·m，工作轉矩區間在0.5～1.2 N·m內，轉矩波動相對于初始設計有所改善。

5 結 語

本文提出了一種爪極式有限轉角電機拓撲結構，設計了整體式轉子磁軛、無齒槽定子爪極結構。建立了爪極式有限轉角電機等效磁路模型，推導出爪極式有限轉角電機電磁轉矩解析式，通過解析法和有限元分析確定了電機的結構尺寸和材料屬性。

運用遺傳算法對電機的磁阻轉矩和反電動勢畸變率進行了多目標優化，確定了電機的永磁體極弧系數、定子爪極寬度、氣隙長度、永磁體厚度等參數的最佳設計值。