基于定子錯位的軸向磁通永磁電機齒槽轉矩削弱方法

閆 偉，彭 兵，莊小雨

(沈陽工業大學 電氣工程學院，沈陽 110870)

0 引 言

雙定子單轉子軸向磁通永磁電機因其結構緊湊、功率密度高與高效節能等優點，被廣泛應用于工業牽引、電動車輛和飛輪儲能等場合[1-3]。而永磁電機中固有的齒槽轉矩直接影響著電機的轉矩脈動、振動與噪聲，對電機的正常運行造成不利影響，因此關于齒槽轉矩的解析計算和削弱方法一直是近年來的研究熱點。

為削弱軸向磁通永磁電機的齒槽轉矩，文獻[4]采用田口法對一臺雙定子軸向磁通發電機的槽口寬度、極弧系數和氣隙長度進行優化，在不影響電機功率密度的情況下有效降低了電機的齒槽轉矩。文獻[5]根據麥克斯韋張量理論推導了軸向磁通永磁電機的齒槽轉矩與電磁轉矩的解析公式，并基于該公式，通過變極弧系數法削弱了一臺單定子軸向磁通電機的齒槽轉矩。文獻[6]采用疊加法對分段磁極削弱齒槽轉矩的可行性進行了研究，給出了在整數槽與分數槽兩種情況下的永磁體分段數、分段間隔和分段寬度與齒槽轉矩的解析表達式，并通過有限元計算驗證了此方法削弱齒槽轉矩的有效性。文獻[7]采用分段傾斜磁極與變極弧系數磁極相結合的方法削弱永磁電機的齒槽轉矩，推導了多種分段磁極結構下的齒槽轉矩表達式，給出了削弱齒槽轉矩的最佳極弧系數組合與磁極傾斜角度的計算方法。除上述方法之外，采用不等齒寬、不等槽口寬、增加輔助槽、偏心磁極與磁極偏移等措施均可有效削弱齒槽轉矩[8-12]。

本文提出一種雙定子錯位型結構，利用能量法對該結構的齒槽轉矩進行了解析分析，并通過有限元法驗證了此方法削弱齒槽轉矩的有效性與可行性。

1 雙定子錯位電機齒槽轉矩解析分析

圖1(a)為雙定子單轉子軸向磁通永磁電機的拓撲結構，此電機由2個結構相同的外定子與1個內轉子組成，定轉子沿軸向排列。雙定子錯位型電機是指在其基礎上，將2個定子盤錯位一定的角度，如圖1(b)所示。

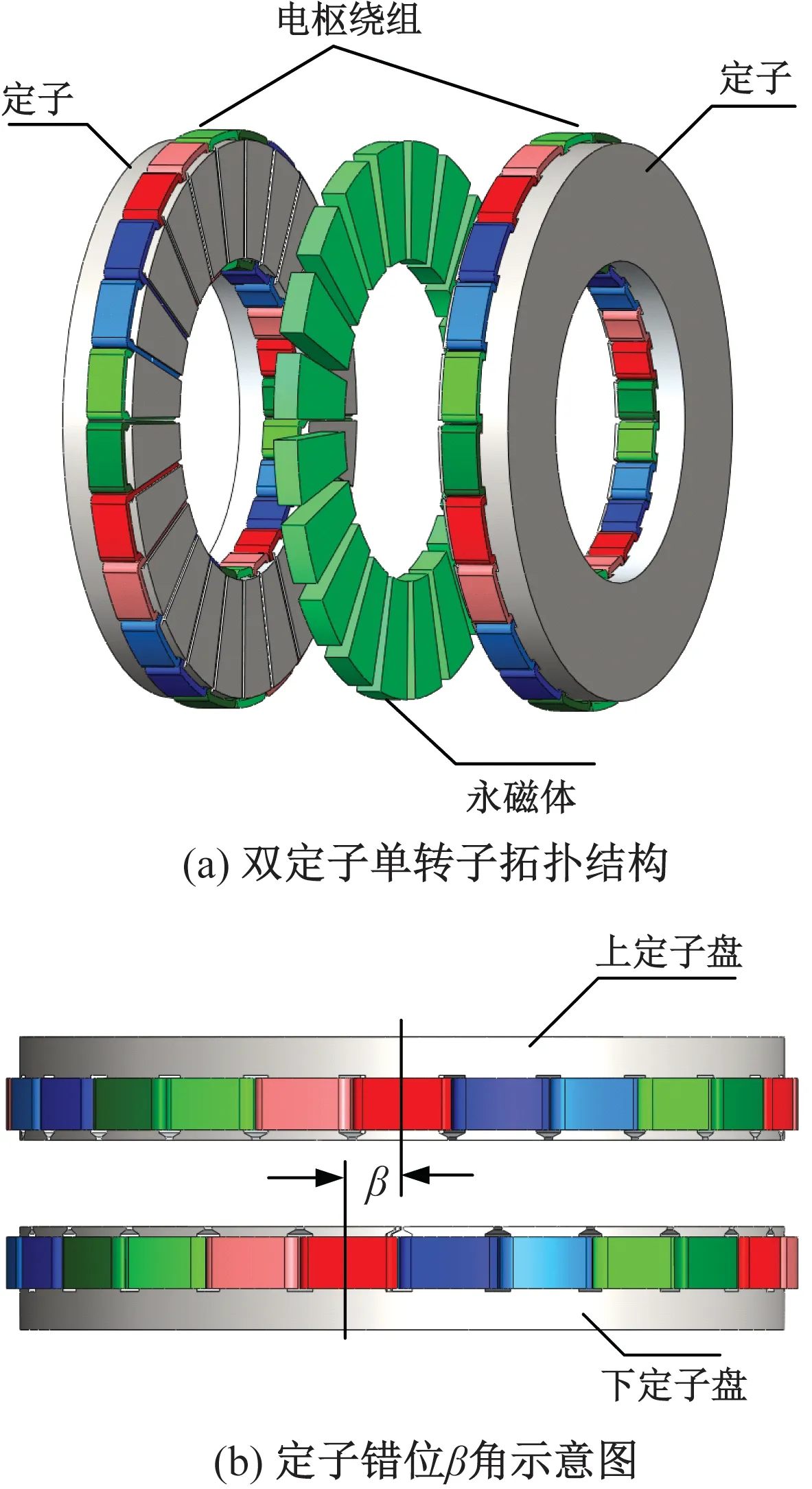
圖1 雙定子錯位型電機結構

對于定子開槽的永磁電機，當定轉子發生相對運動，磁路中磁導發生變化引起磁場儲能變化，便產生齒槽轉矩。將齒槽轉矩定義為永磁電機空載時磁場儲能W對定轉子相對位置角αθ的負導數：

(1)

為便于分析，作出以下假設：

1)鐵心磁導率無窮大；

2)永磁材料的磁導率與空氣相同；

3)θ=0位置設在某一磁極中心線處；

4)在某一半徑處的二維平面分析，不考慮端部效應。

由假設可知，雙定子單轉子軸向磁通電機的磁場能量可認為是永磁體能量與兩側氣隙中的能量之和：

W=Wpm+Wairs+Wairx=

(2)

式中：Wpm為永磁體內的能量；Wairs與Wairx為兩側氣隙中的磁場能量；gs(θ,αθ)、gx(θ,αθ)分別為兩側氣隙有效氣隙長度在圓周方向的分布；hm為永磁體充磁方向的長度；Br(θ)為永磁體剩磁密度；λs(θ,αθ)、λx(θ,αθ)分別如下：

(3)

Br(θ)在某一半徑圓周上的分布如圖2所示。

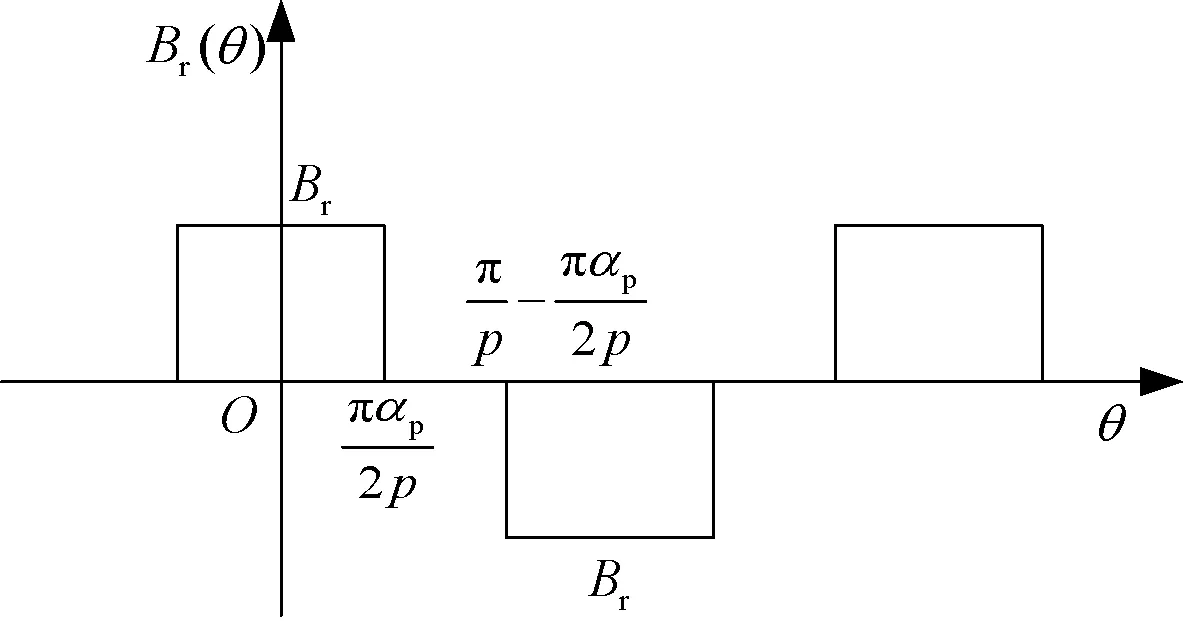
圖2 Br(θ)的分布示意圖

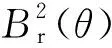
(4)

式中：

(5)

為簡化分析，將定子槽等效為開口槽，如圖3所示。圖3中，bo為槽開口寬度，g0為氣隙長度，β為定子錯位角。

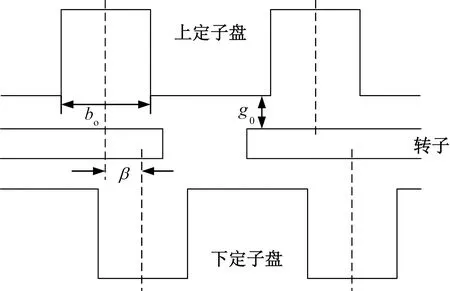
圖3 槽等效模型

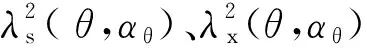
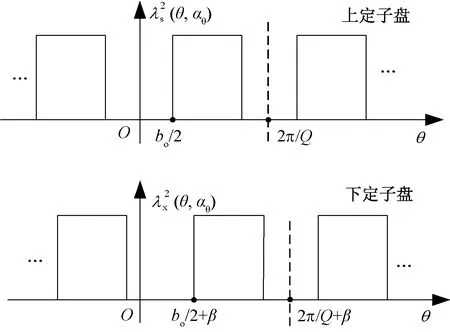
圖的簡化模型

(6)

式中：

(7)

1.3 齒槽轉矩表達式

將式(2)～式(7)代入式(1)，即可得到雙定子錯位型電機的齒槽轉矩Tcog：

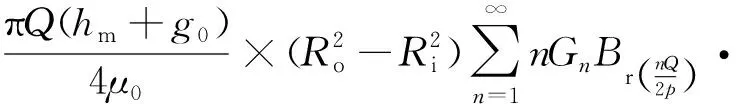
{sin (nQαθ)+sin [nQ(αθ+β)]}=

(8)

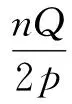
2 基于定子錯位的齒槽轉矩削弱方法

(9)

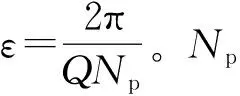
(10)

式中：GCD(Q,2p)為槽數與極數的最大公約數。

令n=mNp，m代表齒槽轉矩的諧波次數，將其代入式(9)，可得β的表達式：

(11)

3 有限元驗證

軸向磁通電機的氣隙磁場呈三維分布，本文采用三維有限元法，以一臺24槽20極電機為例，對錯位前與錯位后的齒槽轉矩進行計算，以驗證錯位結構削弱齒槽轉矩的有效性。永磁電機氣隙磁場分布如圖5所示，電機的主要參數如表1所示。

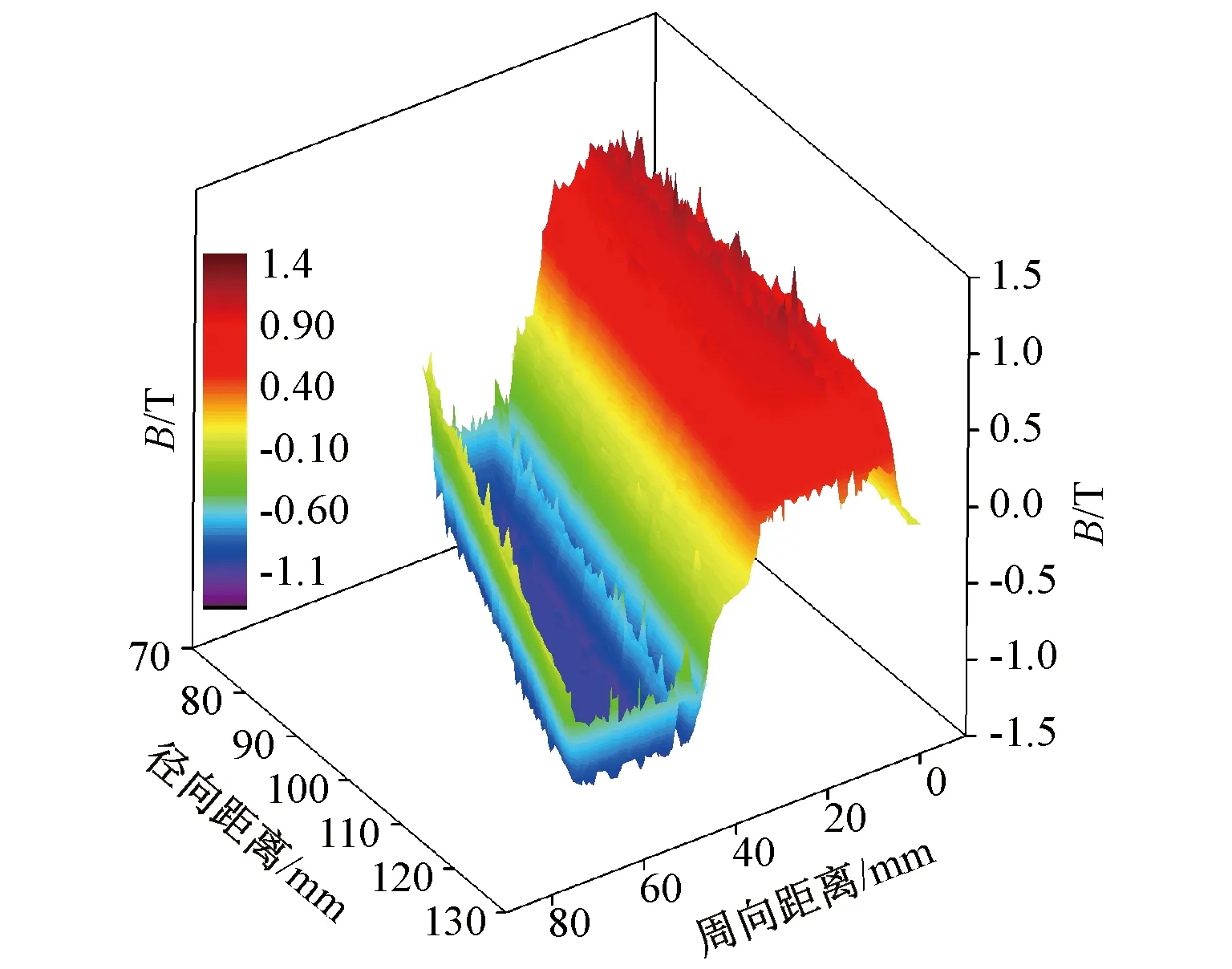
圖5 氣隙磁場分布

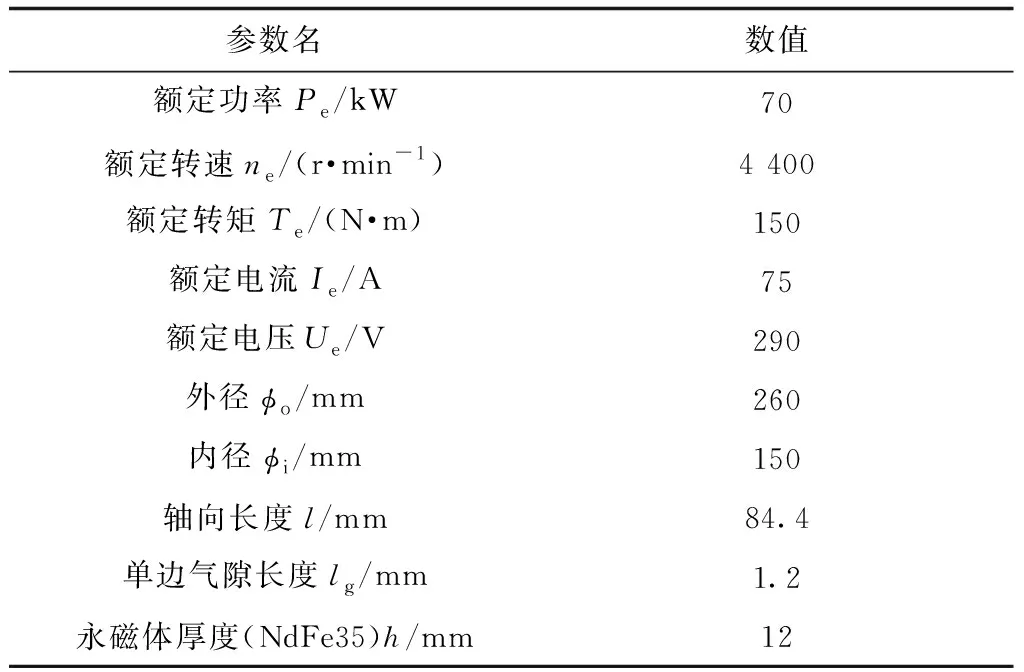
表1 永磁電機主要參數

對于24槽20極電機,GCD(Q,2p)=GCD(24,20)= 4,Np=20/4=5,ε=360°/(24×5)=3°, 一個齒距內齒槽轉矩的周期數Np=5，齒槽轉矩周期為3°機械角度。齒槽轉矩中除基波含量外，其余次諧波的幅值較低，在削弱齒槽轉矩時，應主要削弱基波分量[13]，即取m為1；為盡可能減小定子盤錯位對主磁路的影響，取k為1。由式(11)可知，當兩定子盤錯位1.5°時，可削弱齒槽轉矩中的基波分量。

圖6為定子盤對齊與錯位后的齒槽轉矩對比。可以看出，錯位后顯著削弱了齒槽轉矩。對齊時，齒槽轉矩峰峰值為3.16 N·m，錯位后為0.96 N·m，齒槽轉矩被削弱了69.62%。

圖6 齒槽轉矩對比

圖7為額定負載時的轉矩曲線對比。定子盤對齊時的轉矩平均值為149.83 N·m，錯位后轉矩平均值為150.21 N·m，兩種情況下電機的輸出功率基本保持一致，轉矩脈動由4.33%下降為1.53%。理論上，錯位后電機的額定轉矩相較于對齊時應略有減小。但由于錯位角較小，錯位對主磁路的影響十分微弱，加上三維模型的剖分網格數有限，造成了一定的計算誤差，導致了仿真結果中對齊時的電磁轉矩略微小于錯位后的電磁轉矩。

圖7 額定轉矩波形對比

4 結 語

本文得出了雙定子錯位結構削弱雙定子軸向磁通永磁電機齒槽轉矩的方法。基于能量法推導了兩定子錯位后齒槽轉矩的表達式，并根據表達式得出了可削弱齒槽轉矩的錯位角；以一臺24槽20極電機為例，利用有限元軟件對其仿真，結果表明，錯位后電機的齒槽轉矩與額定負載下的轉矩脈動均得到了有效削弱，并且錯位前與錯位后電機的輸出功率基本保持不變。