充電樁三相AC/DC雙向變換器控制策略研究

施文燁 何志琴 朱佑滔

（貴州大學，貴陽 550025）

主題詞：充電樁 雙向變換器 空間矢量脈寬調制技術 有源功率因數校正 建模仿真

1 前言

近年來，新能源汽車發展迅猛，但目前仍然面臨著許多技術瓶頸，如充電樁的充電效率、電能質量以及只能被動單向充電等。文獻[1]研究表明，不同的充電樁結構對電能的質量有很大影響。文獻[2]研究表明，三相電流型脈寬調制（Pulse Width Modulation，PWM）整流器輸出的直流電壓低于輸入電壓的峰值，且由于輸入電流不連續，其功率因數較低。文獻[3]闡明，傳統整流裝置的功率因數通常在0.45～0.75 范圍內，所以傳統大功率整流器所產生的諧波會嚴重影響電網的電能質量。文獻[4]提及，J.W.Kolar 教授提出了三相VIENNA 整流電路，雖然實現了升降壓輸出，但其開關損耗較大，同時不能實現電能的雙向變換，控制電路的參數設計較為困難。文獻[5]所研究的T 型三電平電路具有中點續流的能力，降低了開關導通損耗，改善了輸出紋波且可以實現電能的雙向流通，但其主電路結構和控制電路較為復雜，開關元器件較多，內管應力較大。文獻[6]～文獻[10]提到，對于混合微電網而言，連接交流母線和直流母線的AC/DC 雙向變換器對系統電壓的穩定和電能質量的提高產生了巨大的影響。針對上述問題，本文提出一種三相AC/DC雙向變換器，給出在整流和逆變2種模式下的數學模型和空間矢量脈寬調制（Space Vector Pulse Width Modulation，SVPWM）控制策略，并利用MATLAB/Simulink搭建仿真模型驗證該方案的可行性。

2 三相AC/DC雙向變換器數學模型

圖1所示為三相AC/DC雙向變換器的拓撲結構，其中，、、為網側三相電壓，、、為網側三相電流，為電路等效電阻，為網側電感，、分別為直流母線電壓、電流，為直流側濾波電容，為負載電阻。在整流模式下（逆變模式過程相同），三相靜止坐標中的數學模型為：

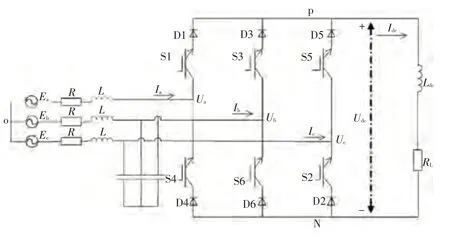
圖1 變換器電力拓撲結構

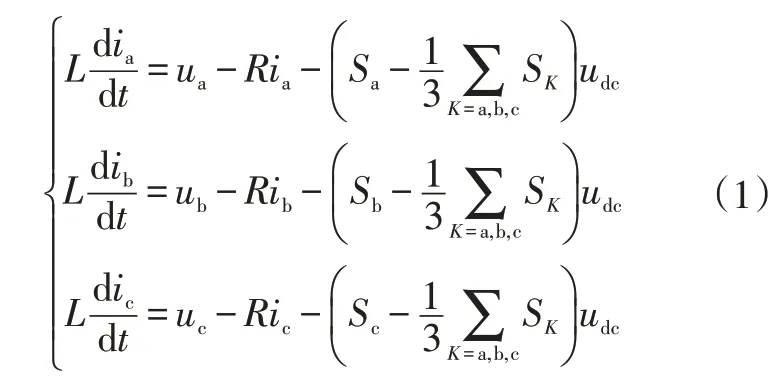
式中，S(=a,b,c)為各相上、下橋臂的導通狀態，S=1 為上橋臂導通，S=0為下橋臂導通。

將式（1）簡化，再經派克（Park）、克拉克（Clark）變換后得到其在同步旋轉坐標系下的數學模型為：

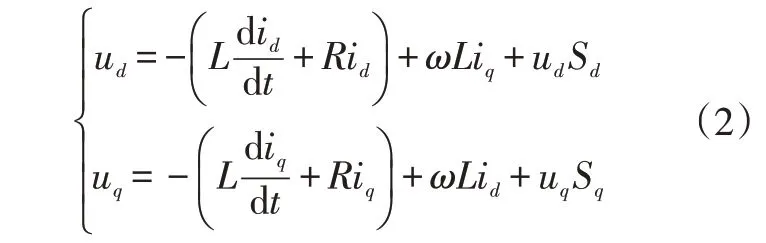
式中，為坐標系的旋轉角頻率；u、u、i、i分別為電壓矢量、電流矢量在、軸上的分量；S、S分別為導通狀態在、軸上的分量。

在u和u中存在、分量互相耦合，不利于控制器的設計，故需對式（2）進行拉普拉斯變換：

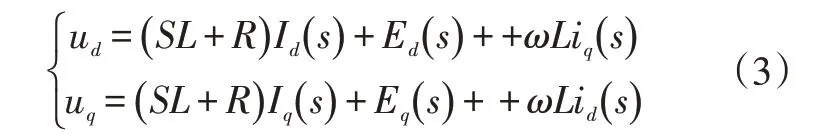
式中，U、U分別為電壓外環的有功指令電壓和無功指令電壓；E()、E()、I()、I()分別為uS、uS、i、i的拉普拉斯變換結果。

對式（3）進行前饋解耦后，設在旋轉坐標系下電壓指令公式為：

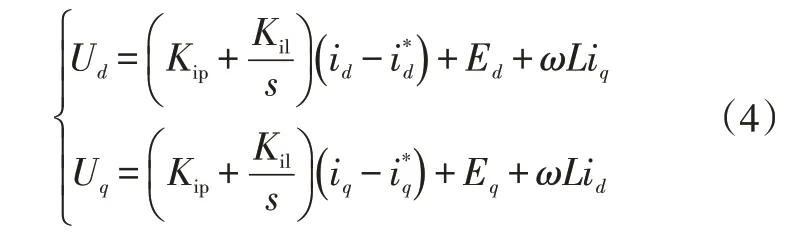
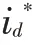
結合式（1），為了消除ωLi、ωLi、E和E的影響，簡化設計，將式（4）改寫為：

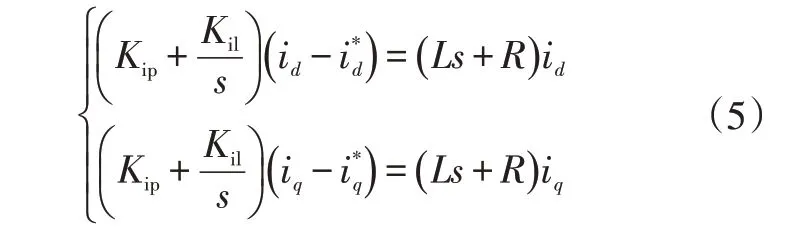
由式（5）可知，、分量已完全分解，只需確定PI調節器的和，即可實現其對電流內環的控制。

3 三相雙向變換器有源功率因數校正控制策略

3.1 矢量合成基本原則

有源功率因數校正（Active Power Factor Correction，APFC）技術是將時變的交流量通過Park、Clark 變換為、分量并使用SVPWM 算法，最終實現電能的雙向變換。由圖1，在整流模式下，網側輸入三相電壓的數學模型為：

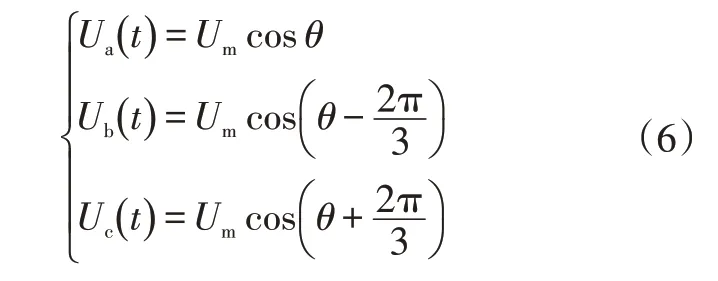
式中，=2π為相位角初始值；為相電壓的有效值；為交流電壓頻率。

則三相電壓合成空間矢量()的表達式為：

由式（7）可知，()是旋轉的空間矢量，幅值為相電壓的1.5 倍，并按逆時針方向以角頻率=2π勻速轉動。根據電路上、下橋臂的導通狀態可形成8 種組合，即6 個非零矢量和2 個零矢量，由式（7）可得到8個基本矢量的幅值及其所在矢量平面內的相位，如圖2 所示。

由圖2可知，系統被劃分為6個扇區，每個扇區內的合成矢量都可由～合成。

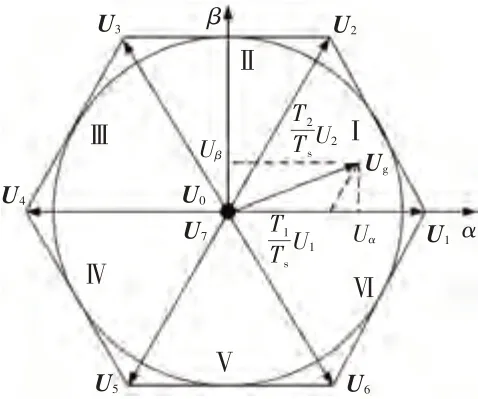
圖2 空間電壓矢量分布及合成

3.2 矢量作用時間

以第1扇區為例，電壓空間矢量的合成與分解如圖3所示，由圖3推導可知：

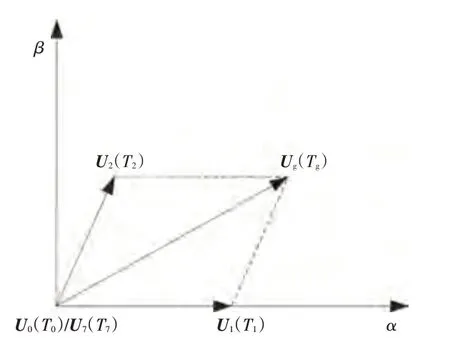
圖3 電壓空間矢量在第1扇區的合成與分解

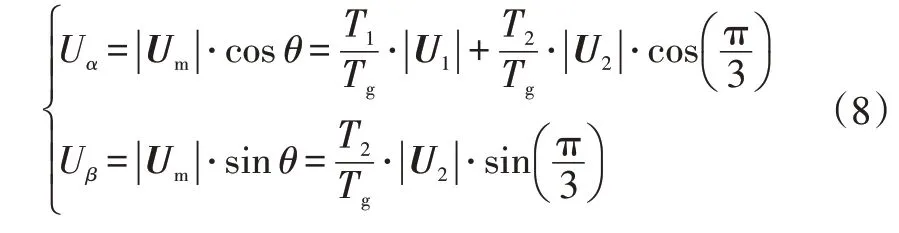
式中，U和U分別為相電壓的模在兩相靜止坐標系軸和軸上的投影；、分別為相鄰作用矢量、的作用時間；為合成矢量的作用時間。

將式（8）簡化后得到扇區內矢量的作用時間為：

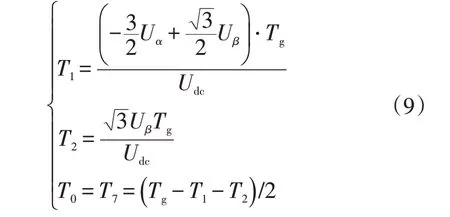
通過以上推導可知，開關管存在同時導通和關斷的情況，經過分析，只需通過調整驅動程序即可解決，不需要額外加死區時間避免直通。上述矢量合成的方法同樣適用于逆變模式。

4 PI控制器參數設置

圖4 所示為整流模式下矢量控制系統結構。在旋轉坐標系下，由式（2）可知，U與U之間存在相互耦合，所以應采取前饋解耦控制，并采用PI 調節器進行調節，從而實現軸與軸的獨立控制，提高系統動態性能。

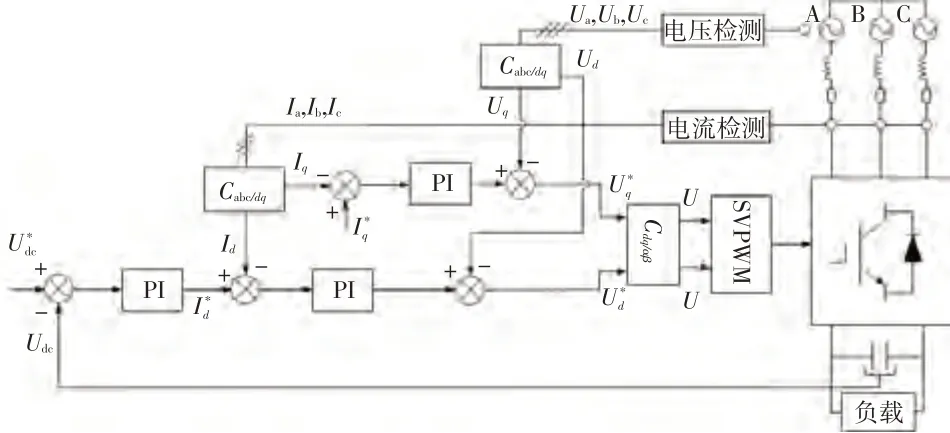
圖4 矢量控制結構

前饋解耦后由式（5）分析可得，在實際分析中，還需考慮電流采樣延時和變換器本身的時間常數等影響，電流內環結構如圖5所示，其中為PWM波形的增益。

圖5 電流內環結構

按Ⅰ型系統設計，盡量使PI 調節器的零點與電流控制傳遞函數的極點相消，令=/τ，τ=/，同時，將圖5 中的電流采樣周期合并，并考慮阻尼比=0.707的Ⅰ型系統的二階最佳系統，經校正，結合電流環的開環傳遞函數，可確定和，其具體表達式為：

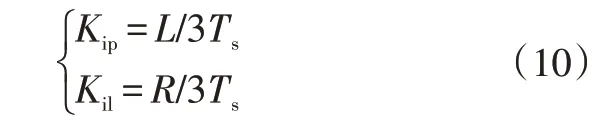
將式（10）代入其閉環傳遞函數，可得：

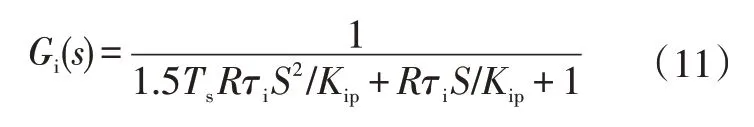
最后考慮開關頻率及的取值，式（11）可簡化為：

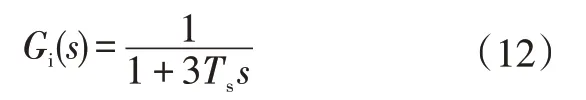
由以上分析可知，只要系統的開關頻率足夠高，電流內環即可得到快速動態響應，本文的開關頻率為10 kHz，所以響應速度已得到滿足。

在整流模式下，開關管的通斷頻率遠大于網側電動勢基波頻率，故可以忽略PWM諧波分量，只考慮開關函數的低頻分量，因此開關的函數表達式為：

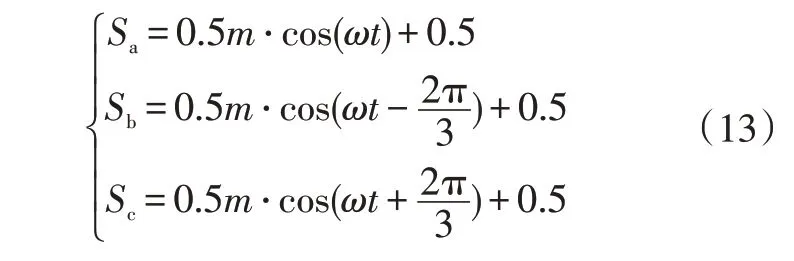
式中，為PWM調制比。

整流模式下系統交流側的電流為：

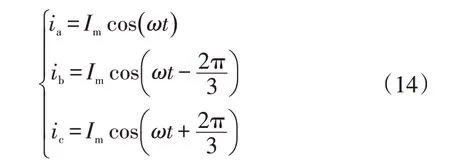
式中，為相電流的有效值，則對應直流側輸出為：

將式（13）和式（14）代入式（15），經簡化可得：

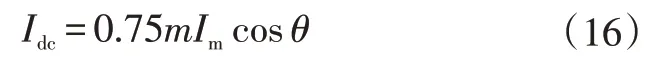
則其電壓外環控制結構如圖6 所示。電壓外環PI控制器的主要作用是穩定直流側的輸出電壓，故從抗干擾角度出發，選用Ⅱ型系統，由圖6 可得電壓環的開環傳遞函數()為：

圖6 電壓環控制結構

式中，為系統電壓環的位置誤差系數；為系統電壓環的指數系數；為系統電壓環隨機選取的周期。

在圖6 中，i為電感電流。又由電壓外環頻寬=/，根據工程設計方法中Ⅱ型系統參數計算公式可得：

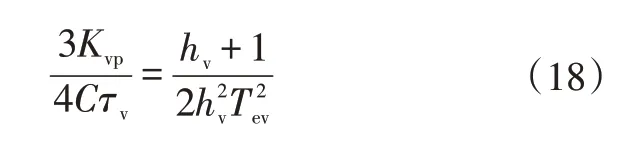
在實際工程應用中，系統的抗干擾和系統跟隨性都會綜合考慮電壓外環頻寬=5，將其代入式（18），可得電壓外環PI調節器的比例和積分系數分別為：

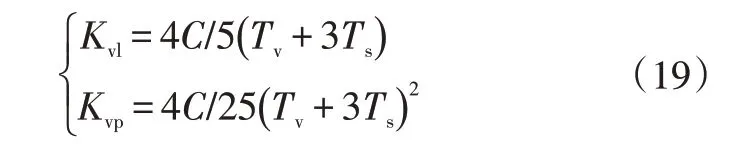
式中，為系統電壓環的靜態速度誤差系數；為系統電壓環PI 調節時間；為系統電壓環總的作用時間。

經上述分析確定了電流電壓外環PI 控制參數，減少了試驗中參數選擇的盲目性，但在實際應用中，由于設備參數不統一，還需根據實際情況進行微調，以求得最優參數取值。經過驗證，整流模式下PI 控制器參數的確定方法同樣適用于逆變模式。

5 仿真與結果

本文針對三相AC/DC 雙向變換電路，采用前饋解耦的雙閉環控制策略和SVPWM 的調制策略來控制功率開關管通斷，利用MATLAB/Simulink仿真軟件平臺搭建仿真模型，如圖7所示。

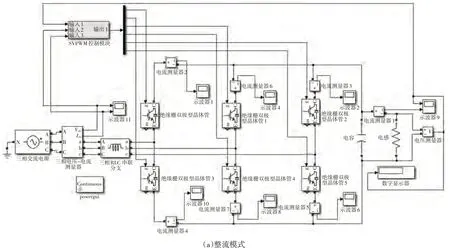
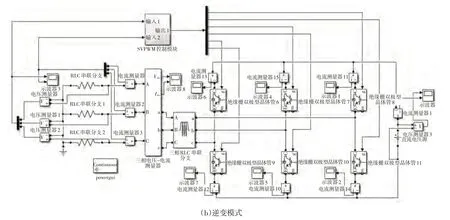
圖7 系統在不同模式下的仿真模型

仿真參數設置為：交流側相電壓=220 V，頻率=50 Hz，直流側輸出電壓=400 V，輸出功率=4 kW，開關頻率=10 kHz，交流測電感=3.3 mH，電路等效電阻0.05 Ω，直流側濾波電容=1 200 μF。仿真波形如圖8 所示。

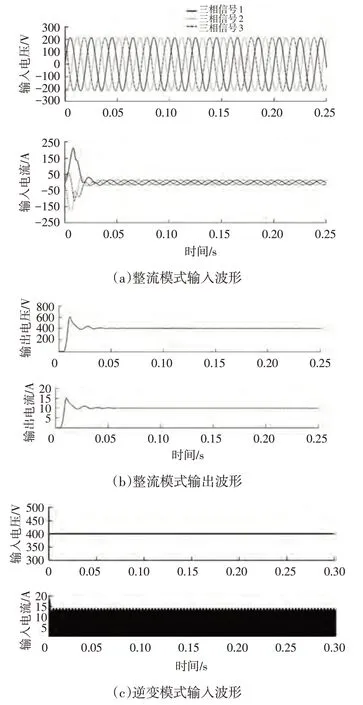
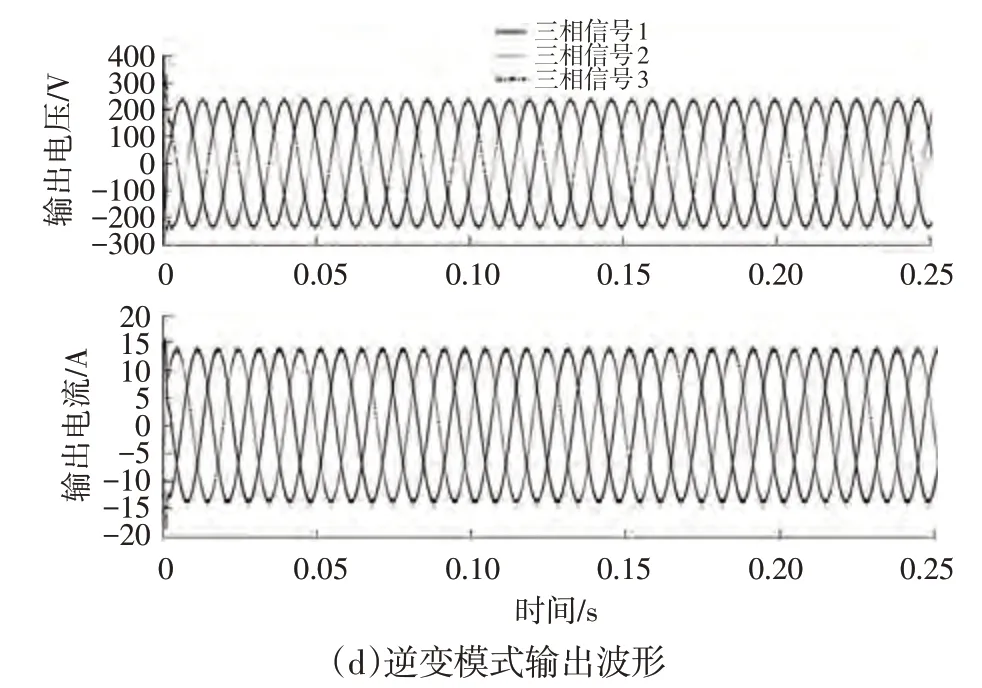
圖8 系統在不同模式下的仿真波形

由圖8a可知，系統起振初期，因直流側接了較大的濾波電容，輸入電流呈現出較大的電流過充。持續約0.02 s后，輸入電壓與電流保持同相位，實現系統在整流模式下在單位功率因數狀態運行。由圖8b 可以看出，外環電壓經過PI調節器能夠敏銳地追蹤外觀指令電壓（400 V），調解時間約為0.02s，實現輸出電壓的穩定追蹤，且輸出的電壓和電流可根據電池的充電需求隨時調整。由圖8d可知，電流呈正弦波且與電壓同相位，符合相關并網技術標準。

圖9 所示為整流模式下交流側的諧波分析結果，在整流模式下交流側的總諧波失真（Total Harmonic Distortion，THD）為0.87%，遠小于5%，電能質量所受干擾明顯減小。圖10所示為逆變模式下交流側的諧波分析結果，逆變模式下的總諧波失真為3.12%，可以看出，變換器的電流諧波含量低，實現了變換器高功率因數運行。對比文獻[3]和文獻[5]，該拓撲結構的總諧波失真明顯降低。

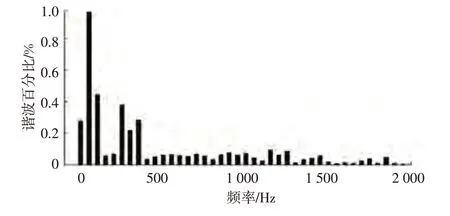
圖9 整流模式下交流側的諧波分析

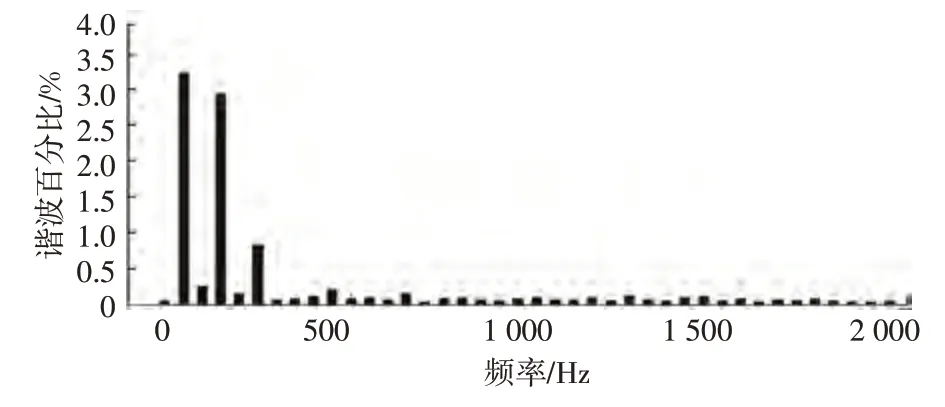
圖10 逆變模式下交流側的諧波分析

對試驗樣機進行相應試驗，圖11所示為原理樣機，圖12所示為上電后功率開關管的驅動信號。

圖11 試驗原理樣機

圖12 功率開關管的驅動信號

系統在整流模式下的輸入、輸出波形如圖13 和圖14所示。

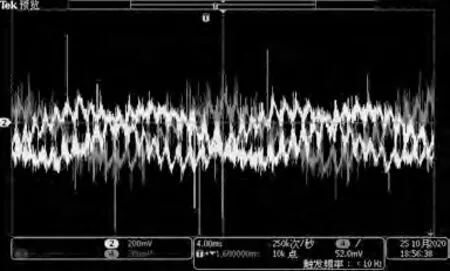
圖13 輸入三相電壓波形

圖14 輸出電壓值

系統在逆變模式下的輸入、輸出波形如圖15 和圖16所示。

圖15 輸入電壓值

圖16 輸出電壓波形

系統的功率如圖17 所示，通過對比圖15 得出系統的傳輸效率為96.44%，對比文獻[3]和文獻[5]，效率均有所提升。

圖17 輸出功率

6 結束語

本文提出了一種三相AC/DC 雙向變換器拓撲結構，并提出了相應的SVPWM 調控策略，通過引入有源功率因數校正技術，使得系統能夠在單位功率因數下運行，并減少了電網諧波，能夠實現能量的雙向流動。經分析，變換器無直通問題，可以不外加死區，直流側電壓可調，減少了變換器對于電能質量的影響，并通過MATLAB/Simulink 仿真平臺驗證了該方案的可行性及優勢，最后利用原理樣機進行試驗，結果表明，系統可實現電能的雙向變換、高功率因數運行，并進一步提高了電能的傳輸效率。