基于新最速下降算法的自適應波束形成

王 帥, 向建軍, 彭 芳, 唐書娟, 李志軍

(空軍工程大學航空工程學院, 陜西 西安 710038)

0 引 言

陣列天線相較于傳統單天線具有空間分辨率高、探測距離遠、抗干擾等優點，目前被廣泛應用于雷達、聲吶、無線通信、空間遙測等領域。例如：在相控陣雷達探測領域，陣列信號處理的應用能夠增強目標信號，抑制干擾信號，提高空間探測的分辨率；在陣列麥克風領域中，對語音信號進行增強，從噪聲中提取清晰的語音信號，提高話音質量；在無線通信領域中，提高能量和信道的利用率，提升譜效率；在水下聲吶探測領域中，對目標進行識別、跟蹤和定位，濾除噪聲影響，提高檢測效率。

波束形成又稱空域濾波，能夠控制陣列天線收發波束的空間指向，是陣列信號處理的代表性技術之一。波束形成通過對陣列天線各陣元施加不同的復數權值，令各信號之間相互干涉，使得陣列天線輸出的信號在目標方向形成主瓣波束，在干擾方向形成盡可能低的零陷來抑制干擾信號的影響，同時盡量降低旁瓣電平來減小雜波的影響。

自適應波束形成是波束形成技術的一種，可以根據目標和干擾的方向，以特定自適應準則自動調節波束指向及零陷，在目標探測和干擾對抗方面發揮了重要作用，具有重大的研究價值和實際意義。經典的自適應波束形成算法包括以下幾種：基于最小均方(least mean square，LMS)算法的自適應波束形成，該算法基于LMS誤差準則，應用該準則構建目標函數，通過梯度下降法求解目標函數的最優解，用最優解進行波束形成。基于遞歸最小二乘(recursive least square， RLS)算法的自適應波束形成遵從LMS誤差準則，該算法采用遞歸的方式代替矩陣求逆，相較于通過矩陣求逆的運算方式求維納解，降低了算法的運算量。最小方差無畸變響應(minimum variance distortionless response, MVDR)波束形成算法基于最大信干噪比(signal to interference plus noise ratio, SINR)準則。該準則使波束形成器輸出的干擾加噪聲功率與信號功率之比最大來求解波束形成器的最優復權系數，因此一般情況下又被看作是最優波束形成。

1 自適應波束形成的原理

自適應算法可以根據背景環境以一定的準則自動調節陣元的權值。有很多準則可以用來調節權值,波束形成里常用的準則有4種,分別是LMS準則、SINR準則、最大似然比準則和最小噪聲方差準則。

最常用的自適應算法是LMS算法,LMS算法因為結構簡單、容易實現、計算量小等優點被廣泛應用于各種領域,如自適應噪聲對消、自適應信道均衡、自適應波束形成等。

其中,基于LMS算法的自適應波束形成采用的是LMS準則,其算法結構如圖1所示。

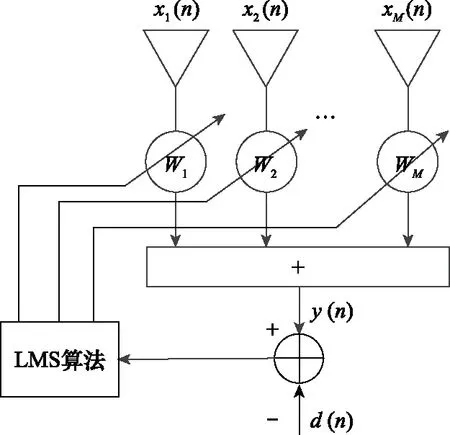
圖1 LMS自適應波束形成算法結構圖Fig.1 LMS adaptive beamforming algorithm structure diagram

圖1中，()代表輸入信號,()代表輸出信號,()代表期望信號,LMS準則就是通過調節各個陣元的權矢量使陣列輸出信號與期望信號的均方誤差達到最小。

梯度下降算法的權向量迭代公式如下:

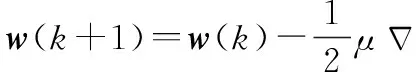
(1)

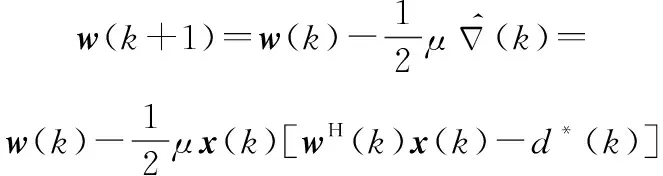
(2)

由于LMS算法具有收斂速度慢,且迭代步長的選擇不靈活的缺點,本文引用文獻[31]提出的一種改進的LMS算法。文獻[31]所提出的算法使迭代步長基于對數函數進行變化,改善了經典LMS算法收斂速度慢且步長固定的缺點,基于對數函數變步長的方式也使得該方法的計算復雜度變大了,沒有LMS那么簡單易實現,同時還引入了參數和參數,這兩個參數的選擇需要依靠經驗,使得該方法在應用時更加復雜。

改進LMS算法的迭代步長的更新公式如下所示:

()=lg(|()(-1)|)=lg[|(()()-())· ((-1)(-1)-(-1))|]

(3)

式中:參數和參數控制著曲線的形狀和整體數值的大小。

將式(3)代入式(2)的迭代公式中，得到基于改進的LMS算法波束形成迭代公式:

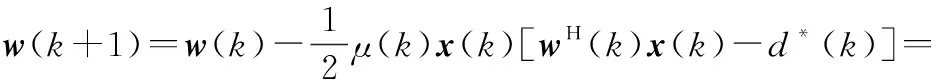
(4)

2 新最速下降波束形成算法的推導

2.1 新最速下降算法

本文提出一種最速下降算法,這種新最速下降算法將高維二次凸優化問題降解到二維上,利用拋物線性質采用循環迭代求解的方式求得高維凸優化問題的最優解。即該方法首先將多元二次凸函數降解為一元二次函數,一元二次函數是一條拋物線,利用拋物線的性質求出拋物線的極值點,通過循環迭代的方式使每次迭代求出的極值點向多元二次凸函數的極值點逼近,最終使結果收斂到多元二次凸函數的極值點。

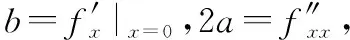
詳細的推導過程如下:

假設多元二次函數的一般形式為

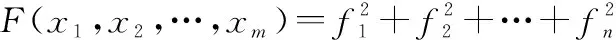
(5)

式中:

=++…+1+=++…+2+?=1+2+…++

一般形式中代表函數中自變量的個數,代表約束方程的數量。可以通過本文提出的新最速下降算法來求取函數的極值,新最速下降算法的迭代過程如下所示:

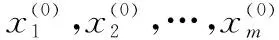
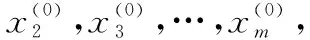
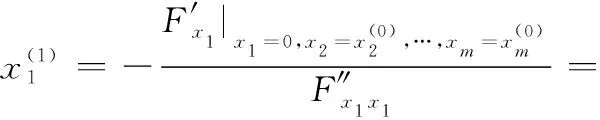
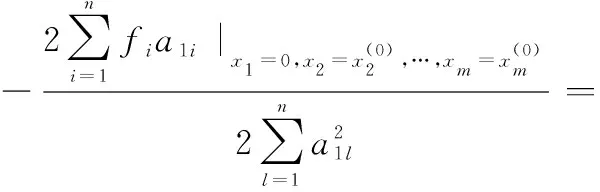
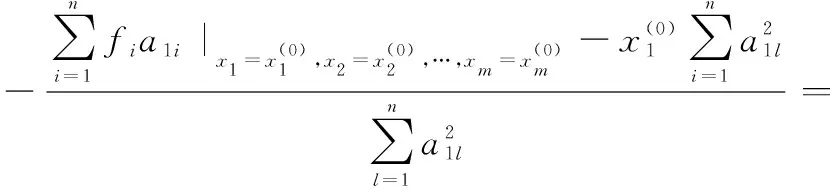
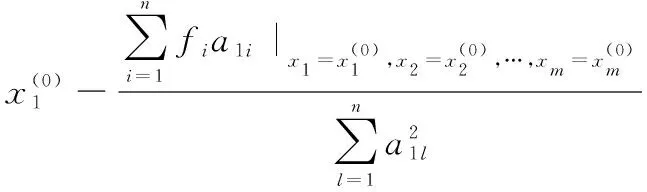
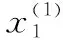
將步驟4中求出的極值點賦值給各個變量,進行循環求取各個變量的極值點,隨著迭代次數的增多,各個變量的極值點將越來越逼近于多元函數的極值點。

最終得到的迭代公式如下所示:

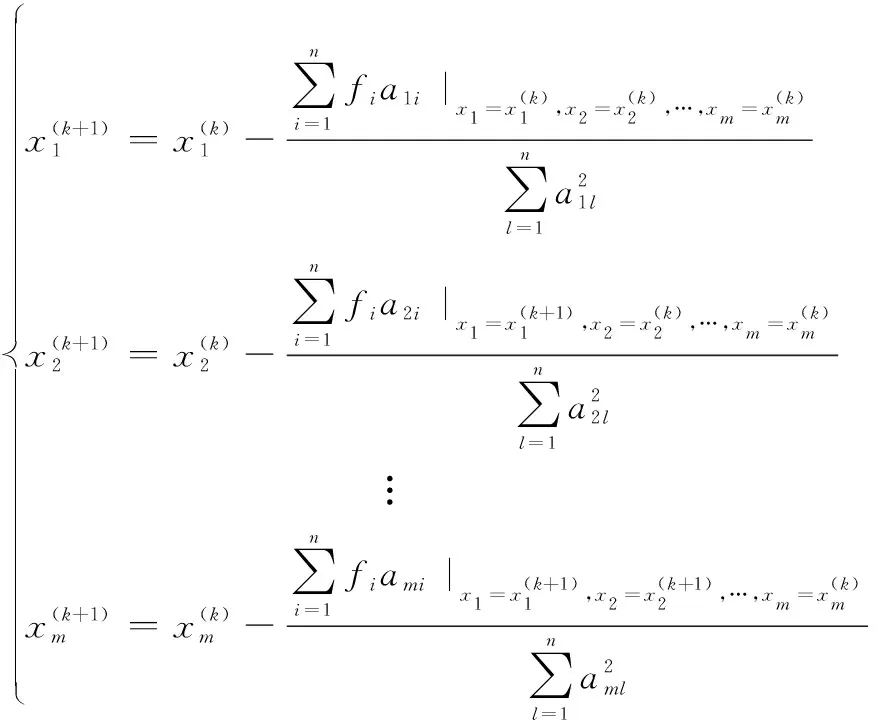
(6)

2.2 基于新最速下降的自適應波束形成算法

本文提出的自適應波束形成算法基于LMS準則,LMS準則是指選取合適的陣列權系數使輸出信號與期望信號之間的均方誤差最小。

陣列輸出信號與期望信號之間的均方誤差函數如下:

()=E[|()()-()|]=

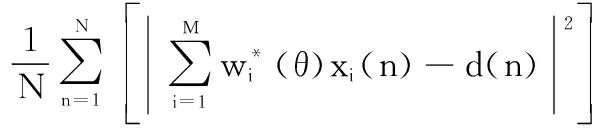
(7)

式中：()代表施加在陣列上的權系數向量；E[·]代表求平均；|·|代表取模。

可以看出均方誤差函數即式(7)符合多元二次函數的一般形式,所以可以采用本文所提出的新最速下降算法求解均方誤差函數的極值點。

對式(7)求一階導數和二階導數得

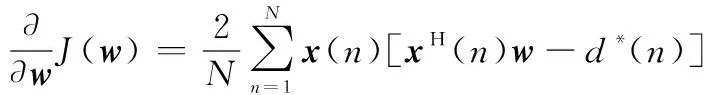
(8)

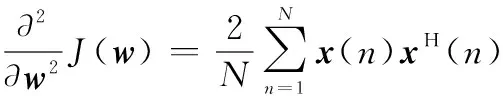
(9)

令

()=()-()

(10)

將式(8)～式(10)的結果代入到式(6)中可以得到權系數的迭代公式:

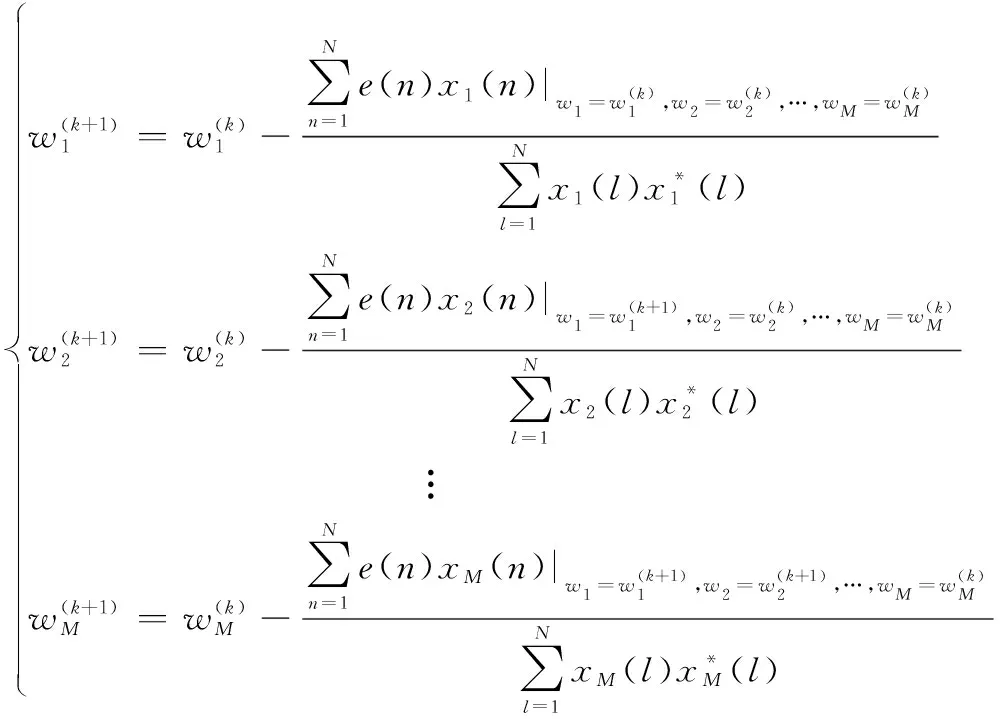
(11)

綜上,本文所提出的自適應波束形成算法的步驟可以概括如下：

設定約束方程的數量,對權系數隨機賦予初值。

采用式(11)對各個權系數變量進行迭代計算。

進行完一次迭代運算之后,根據約束方程數量對迭代方程中的系數進行更新，即對期望信號和輸入信號進行更新,即將期望信號和輸入信號以約束方程數量為一組在所有快拍信號中向后滑動一位,即由之前的()(=-+1,-+2,…,)和()(=-+1,-+2,…,)更新為()(=-+2,-+3,…,+1)和()(=-+2,-+3,…,+1)。

使用更新之后的系數重新進行下一次的迭代運算,即重新進行步驟2。

循環執行步驟2～步驟4,直到進行到最后一個快拍的數據,保存最后計算所得的權系數()(代表快拍數)。

用()對陣列進行加權,陣列的波束形成效果達到最佳。

算法的流程圖如圖2所示。

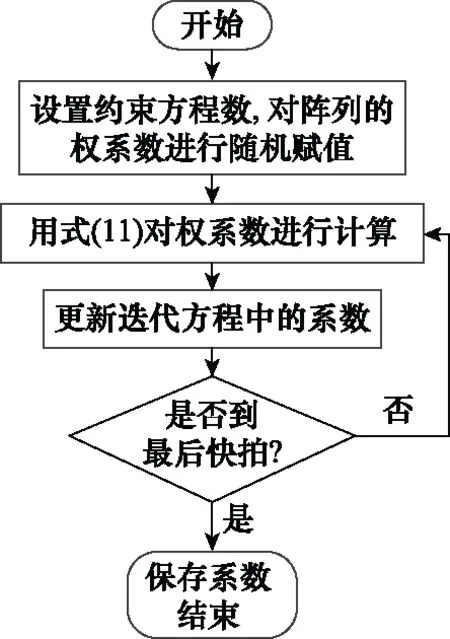
圖2 算法流程圖Fig.2 Algorithm flow chart

3 仿真分析

使用Matlab軟件對波束形成進行仿真模擬,仿真的場景如下:天線陣列是陣元數為16的均勻線陣,干擾的樣式采用壓制性寬帶噪聲干擾,目標信號采用脈寬為10 μs、帶寬為30 MHz、中心頻率為50 MHz的線性調頻脈沖信號。在該場景下對算法性能進行仿真分析,主要分析的內容如下:新算法相對于經典LMS算法以及文獻[18]中所提到的步長可變、收斂速度更快的改進LMS算法的收斂性的快慢、抗干擾能力的強弱、對樣本數的要求等。

3.1 收斂速度對比

仿真環境設置如下:目標方向設置為0°,干擾方向設置為50°,令信噪比(signal to noise ratio, SNR)為0 dB、干噪比(interference to noise ratio, INR)為20 dB、快拍數=600、進行500次蒙特卡羅仿真、LMS算法的迭代步長設置為在可以保證算法收斂的情況下使算法收斂速度最快的最大允許迭代步長,改進LMS算法中的=1 200,=0000 01,所提算法中的約束方程的數量=5,最終得到陣列輸出信號與期望信號之間的均方誤差與快拍數之間的關系,如圖3所示。

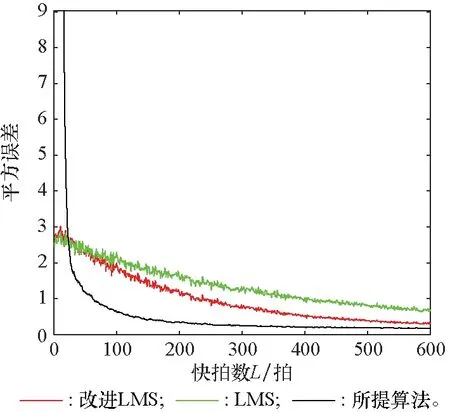
圖3 3種算法收斂速度對比Fig.3 Convergence speed comparison of three algorithms

從圖3中可以看出,隨著快拍數的增多,所提算法最先收斂到最小,改進的LMS算法其次,最后是LMS算法,這說明所提算法的收斂性相較于其他兩種算法更快,在進行波束形成時實時性會更好。

3.2 抗干擾能力對比

由于改進LMS算法的性能要優于經典LMS算法,所以以下分析將只與改進LMS算法作對比。令改進LMS算法的仿真環境中INR分別為10 dB、30 dB、50 dB和70 dB,令新算法的仿真環境中INR分別為50 dB、70 dB、100 dB和150 dB,其他條件均與第3.1節的環境保持一致,得到波束指向圖如圖4和圖5所示。

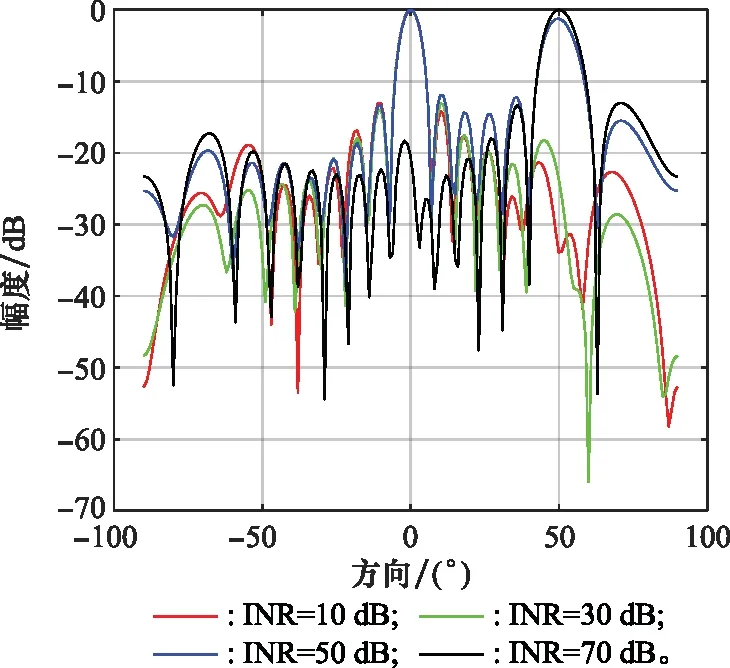
圖4 改進LMS算法抗干擾能力的波束指向圖Fig.4 Beam pattern of improved LMS algorithm anti-jamming ability

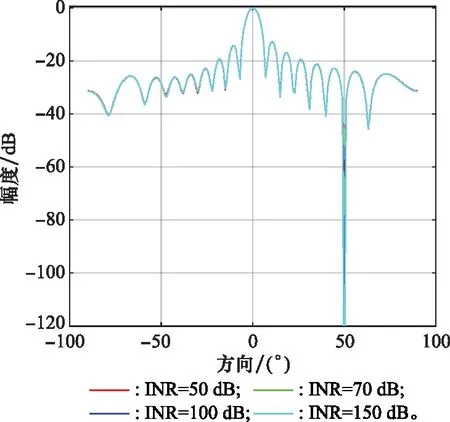
圖5 所提算法抗干擾能力的波束指向圖Fig.5 Beam pattern of the proposed algorithm anti-jamming ability

從圖4中可以看出,當INR=10 dB時,改進LMS算法可以在目標方向形成主波束,在干擾方向處形成凹陷;當INR=30 dB時,改進LMS算法仍然可以在目標方向形成主波束,但是已經無法在干擾方向形成凹陷;當INR=50 dB時,在目標方向形成主波束,但是在干擾方向形成的波束的幅度也接近主波束的幅度,這種情況會大大降低波束形成算法的精度甚至導致無法工作;當INR=70 dB時,在干擾方向形成主波束,在目標方向已經無法形成主波束,此時的波束形成算法已經無法正常工作。

從圖5中可以看出,隨著INR的增大,所提算法的主波束指向一直保持不變,始終指向目標的方向,在干擾的方向始終會形成零陷,而且隨著干擾的增強零陷也會越來越深,對干擾的衰減越來越大，從而消除干擾的影響。

通過圖4和圖5的對比,可以看出所提算法在抗干擾方面有很大優勢。即使INR達到150 dB,所提算法仍然可以正常工作,在目標方向形成主波束,在干擾方向形成深度凹陷。

3.3 抗噪聲能力對比

將改進LMS算法的仿真環境設置為INR=20 dB,快拍數=600,SNR分別設置為0 dB、-10 dB、-20 dB、-30 dB;將所提算法的仿真環境設置為INR=50 dB,快拍數=600,SNR分別設置為0 dB、-20 dB、-40 dB、-60 dB;其他設置均與第3.1節一致,得到波束指向圖如圖6和圖7所示。

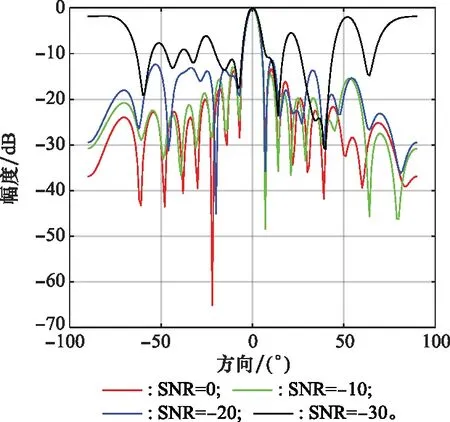
圖6 改進LMS算法抗噪聲能力的波束指向圖Fig.6 Beam pattern of improved LMS algorithm anti-noise ability

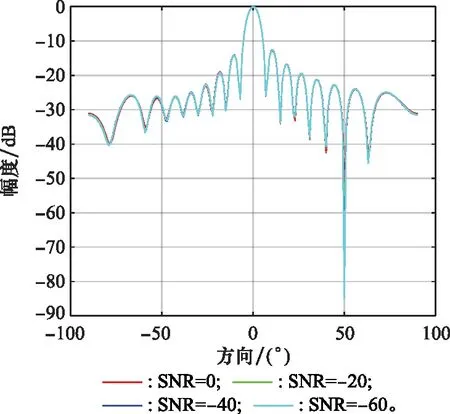
圖7 所提算法抗噪聲能力的波束指向圖Fig.7 Beam pattern of the proposed algorithm anti-noise ability

圖6是改進LMS算法在SNR分別為0 dB、-10 dB、-20 dB、-30 dB情況下所得到的波束指向圖。從圖6中可以看出，當SNR為0 dB時,可以在干擾的方向形成凹陷,在信號方向形成主瓣;當SNR為-10 dB和-20 dB時可以在信號方向形成主瓣,但是無法在干擾方向形成凹陷;當信噪比為-30 dB時波束指向圖嚴重失真,已經無法正常工作。

圖7是新算法在SNR分別為0 dB、-20 dB、-40 dB、-60 dB情況下所得到的波束指向圖。從圖7中可以看出,即使SNR下降到-60 dB時,所提算法仍然可以在干擾的方向形成凹陷,在信號的方向形成主瓣,可以保持正常工作。

綜上,經過對比可以得到結論,所提算法的抗噪聲能力比改進LMS算法要好。

3.4 低快拍數下的性能對比

將改進LMS算法的仿真環境設置為INR=20 dB,快拍數分別設置為100、50、30、10;將所提算法的仿真環境設置為INR=50 dB,快拍數分別設置為100、50、30、10;其他設置均與第3.1節一致,得到波束指向圖如圖8和圖9所示。

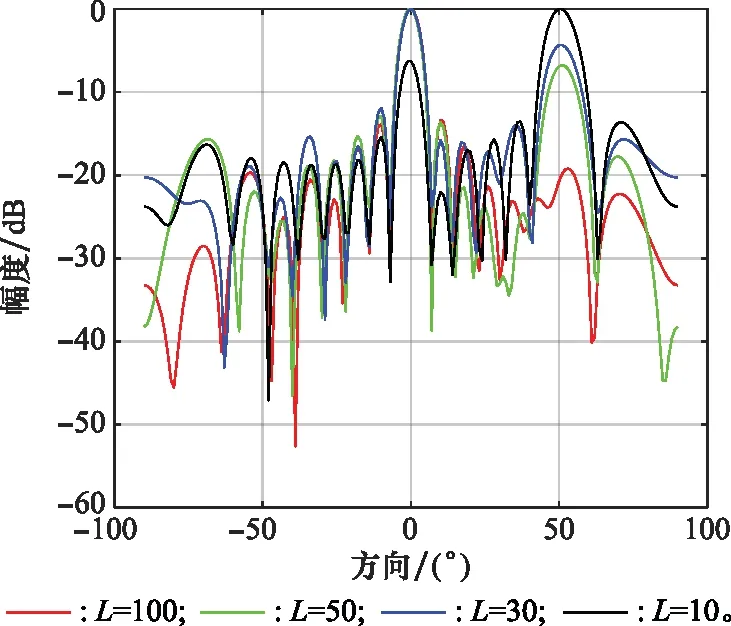
圖8 改進LMS算法低快拍下的波束指向圖Fig.8 Beam pattern of improved LMS algorithm under low snapshot

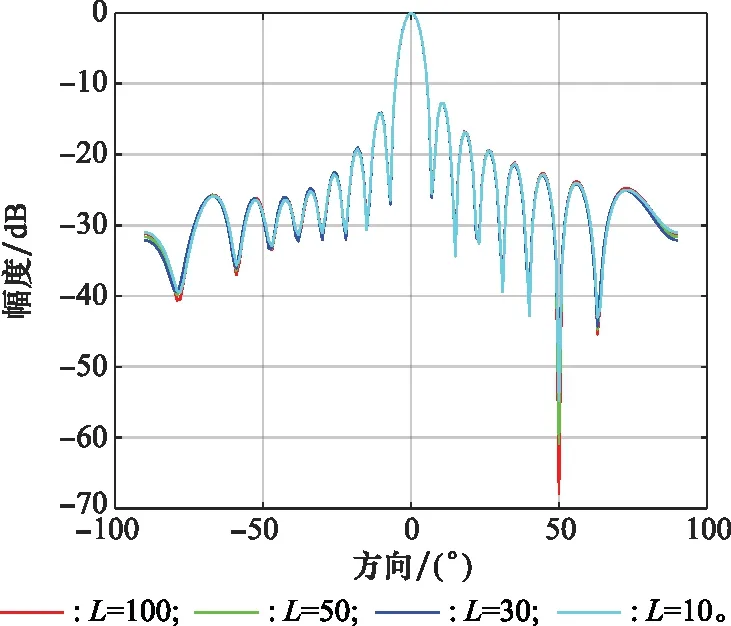
圖9 所提算法低快拍下的波束指向圖Fig.9 Beam pattern of the proposed algorithm under low snapshot

從圖8中可以看出,改進LMS算法在快拍數較少時已經無法在干擾的方向形成凹陷,在快拍數為100、50的時候雖然無法在干擾方向形成凹陷,但是勉強可以在信號方向形成主瓣,在快拍數降到30以下時,改進LMS自適應波束形成無法正常工作。可見改進LMS算法在低快拍的情況下性能不是很好。

從圖9中可以看出,即使是在快拍數很少的情況下,新算法仍然可以在目標方向形成主波束,在干擾方向形成凹陷,實現正常的波束形成并抑制干擾。所以所提算法具有可以在低快拍情況下工作的優點。

3.5 所提算法的抗干擾性能分析

為了對所提算法的抗干擾性能進行分析,引入干信比(interference-to-signal ratio, ISR)作為衡量指標,ISR即干擾功率與噪聲功率的比值。為了直觀地對比干擾和信號的關系,將仿真環境中噪聲功率設置為0,快拍數設置為600,波束形成器輸入的ISR設置為0～200,經所提算法波束形成后得到輸出ISR與輸入ISR的關系,如圖10所示。

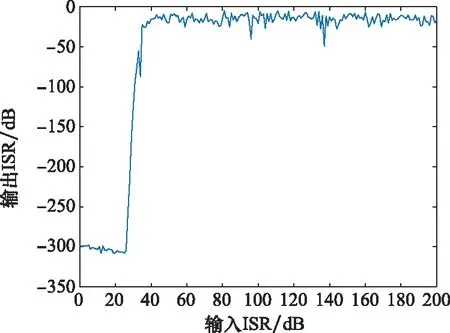
圖10 輸出ISR與輸入ISR的關系Fig.10 Relationship between output ISR and input ISR

從圖10中可以看出,當輸入ISR小于30 dB時,所提算法對輸出ISR具有較大的改善,大約能夠達到300 dB。輸入ISR由30 dB轉向40 dB時,所提算法對輸出ISR的改善會急劇惡化,當輸入ISR為40 dB時,對輸出ISR的改善約為40 dB。當輸入ISR大于40 dB時,輸出ISR始終維持在0 dB左右,隨著輸入ISR的增大,對輸出ISR的改善逐漸增大,但是改善效果不如輸入ISR小于40 dB的階段。綜上,所提算法對干擾的抑制能力在輸入ISR小于40 dB時較強,當ISR大于40 dB時雖然仍然具有一定的抑制能力,但是抑制能力會有一定程度的下降。

接下來分析抗干擾性能與干擾信號數量的關系,將輸入ISR設置為30 dB,分別在不同方向施加1～16個相互獨立的干擾信號,得到輸出ISR，如圖11所示。

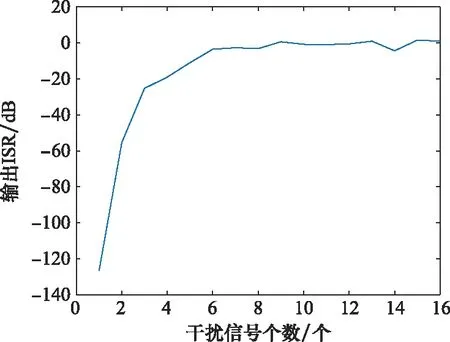
圖11 輸出ISR與干擾數量的關系Fig.11 Relationship between output ISR and the number of interference

從圖11中可以看出,當干擾源的數量少于6個時,隨著干擾源數量的增加,算法對輸出ISR的改善作用逐漸減弱。當干擾源的數量大于6個時,輸出ISR逐漸趨近于0 dB,達到算法的極限。所以當干擾源的數量較少,少于6個時,算法的抗干擾性能較強,當干擾源數量較多時,雖然算法對干擾仍有一定抑制能力,但是效果會變差。

圖12為干擾源數量分別為1、5、9、13時的波束指向圖,可以看到隨著干擾源數量的增加,在干擾方向形成的凹陷減小,即對干擾的抑制能力減弱。當干擾的數量大于6時,波束圖的旁瓣升高,在干擾方向的抑制能力減弱較為明顯,波束形成的性能變差。

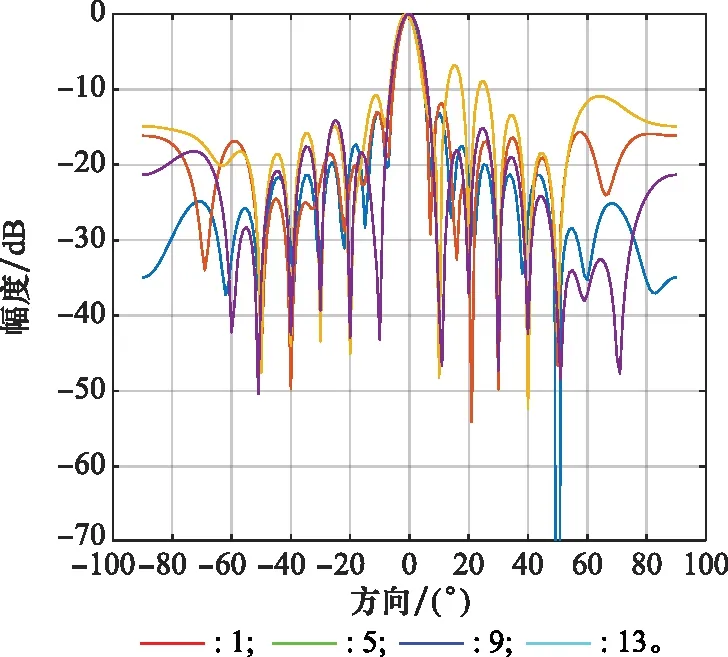
圖12 干擾數量不同時波束圖對比Fig.12 Comparison of beam patterns with different interference numbers

4 結 論

經過仿真分析可以看出，所提出的最速下降算法具有收斂速度快、結果更精確的優點。將該算法用于自適應波束形成,得到基于新最速下降法的自適應波束形成算法，該算法具有以下特點:收斂速度更快,具有更好的實時性;可以對抗強干擾,即使干擾的強度很高,算法都可以在干擾方向形成衰減,在目標方向形成主瓣,保證正常工作;在低快拍數的情況下算法仍然可以正常工作,在干擾方向形成衰減,在目標方向形成主瓣。